VWL 3: Mikroökonomie Aufgabenblatt 4

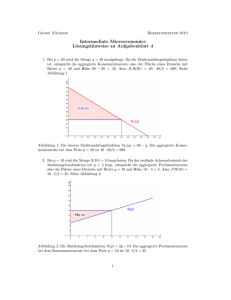
Georg Nöldeke
Frühjahrssemester 2010
VWL 3: Mikroökonomie
Aufgabenblatt 4
1. Ein Gut kann von 20 Unternehmen produziert werden. Die Technologien dieser Unternehmen sind identisch und werden durch die Produktionsfunktion
f (x1 , x2 ) =
√
x1 +
√
x2
beschrieben. Die Marktnachfragefunktion ist im relevanten Bereich durch D(p) = 120−
10p gegeben.
(a) Die Faktorpreise sind (w1 , w2 ) = (1, 1); beide Inputs sind variabel. Bestimmen
Sie Wettbewerbsmenge und Wettbewerbspreis. Wie hoch ist der Gewinn, den ein
Unternehmen bei dem Wettbewerbspreis erzielt?
(b) Nun steige der Preis des ersten Inputs auf w1 = 2, während der Preis des zweiten
Inputs unverändert bleibt. Welche Auswirkungen auf Wettbewerbspreis, Wettbewerbsmenge und Unternehmensgewinne ergeben sich? Unterscheiden Sie bei der
Beantwortung dieser Frage die kurze Frist (Menge des zweiten Faktors ist fix auf
dem in der vorherigen Teilaufgabe gewählten Niveau) und die lange Frist (beide
Inputfaktoren sind variabel).
2. Um in einem Markt aktiv zu werden, muss ein Unternehmen quasifixe Marktzutrittskosten in Höhe von F = 80 aufwenden. Zur Produktion der Outputmenge y entstehen einem aktiven Unternehmen zusätzlich variable Kosten in Höhe von V C(y) = 40y+50y 2 .
Sollte dieses Unternehmen bei einem Outputpreis p = 140 in den Markt eintreten?
3. Die aktiven Unternehmen in einem Markt produzieren jeweils mit der Kostenfunktion
C(y) = 100 + 100y + 4y 2 ;
für inaktive Unternehmen fallen keine Kosten an. Die Marktnachfragefunktion ist im
relevanten Bereich durch D(p) = 1000 − p gegeben.
(a) Bestimmen Sie die kurzfristige Marktangebotsfunktion sowie kurzfristigen Wettbewerbspreis und Wettbewerbsmenge in Abhängigkeit von der Anzahl m, der im
Markt aktiven Unternehmen.
(b) Die Anzahl der Unternehmen, die im Markt aktiv sind, wird durch die Marktzutrittsentscheidungen einer grossen Anzahl von Unternehmen bestimmt. Wieviele
Unternehmen sind in einem langfristigen Wettbewerbsgleichgewicht aktiv?
4. Das Angebot in einem Wettbewerbsmarkt ist fix. Führt die Einführung einer Mengensteuer in einem solchen Markt zu einer Verringerung der aggregierten Handelsgewinne?
1
5. Die Marktnachfragefunktion in einem Wettbewerbsmarkt ist im relevanten Bereich
D(p) = 100 − p. Die Marktangebotsfunktion ist S(p) = 3p.
(a) Berechnen Sie Wettbewerbspreis, Wettbewerbsmenge und die aggregierten Handelsgewinne im Wettbewerbsgleichgewicht.
(b) Der Staat beschliesst, die Produzenten des Gutes dadurch zu unterstützen, dass
er den Marktpreis auf p = 30 festsetzt. Mengen des Gutes, die zu diesem Preis auf
dem Markt nicht abgesetzt werden können, kauft der Staat auf (und vernichtet
sie dann). Wie hoch sind die Ausgaben, die dem Staat für diese Massnahme
entstehen? Wie hoch sind die aggregierten Handelsgewinne?
(c) Anstatt die aufgekauften Mengen zu vernichten, verfährt der Staat nun wie folgt:
Er kauft die gesamte angebotene Menge des Gutes zum Preis von p = 30 auf und
setzt dann einen Verkaufspreis fest, zu dem er die gelieferte Menge auf dem Markt
wieder absetzen kann. Welchen Verkaufspreis muss der Staat festsetzen, damit er
keine Güter mehr vernichten muss? Wie hoch sind die Ausgaben, die dem Staat
in dieser Situation entstehen? Wie hoch sind die aggregierten Handelsgewinne?
(d) Die bisherigen Eingriffe in den Markt werden durch eine Mengensubvention ersetzt. Wie hoch muss der Subventionssatz sein, damit die aggregierte Produzentenrente im Vergleich zu den in den beiden vorhergehenden Teilaufgaben diskutierten Eingriffen unverändert bleibt? Wie hoch sind die bei diesem Subventionssatz resultierenden aggregierten Handelsgewinne?
6. √
Die √
Präferenzrelation einer Konsumentin wird durch die Nutzenfunktion u(x1 , x2 ) =
x1 x2 dargestellt.
(a) Bestimmen Sie die indirekte Nutzenfunktion.
(b) Das Einkommen der Konsumentin beträgt m = 100. In einer Ausgangssituation
sind die Preise durch (p1 , p2 ) = (4, 1) gegeben. In einer neuen Situation fällt
der Preis von Gut 1 auf p01 = 1. Wie hoch ist die Hicks-Kompensation dieser
Preisänderung?
(c) Ausgehend von der neuen Situation mit p01 = 1 steigt der Preis von Gut 1 wieder
auf den Ausgangswert p1 = 4 an. Wie hoch ist die Hicks-Kompensation dieser
Preisänderung?
7. Eine Konsumentin mit artiger Präferenzrelation hat im Jahre 2007 das Güterbündel
(xb1 , xb2 ) = (20, 30) bei Preisen von (pb1 , pb2 ) = (20, 30) konsumiert. Im Jahr 2008 beträgt
ihr Einkommen mt = 1020; die Güterpreise sind (pt1 , pt2 ) = (6, 30). Können Sie sagen,
in welchem der Jahre es der Konsumentin besser geht?
8. In der Vorlesung wurde mit Hilfe der indirekten Nutzenfunktion argumentiert, dass eine Mengensteuer auf ein Gut einen Konsumenten schlechter als eine Kopfsteuer stellt,
die zu den gleichen Steuereinnahmen führt. Was gilt für den entsprechenden Vergleich einer Mengensubvention und einer Kopfsubvention, die dazu führen, dass der
Konsument die gleiche Subventionszahlung erhält? Fertigen Sie hierzu eine geeignete
Abbildung an.
2