VWL 3: Mikroökonomie Lösungshinweise zu Aufgabenblatt 4

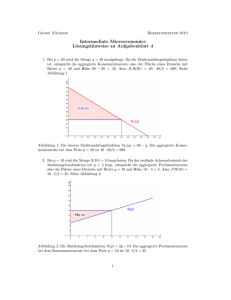
Georg Nöldeke
Frühjahrssemester 2010
VWL 3: Mikroökonomie
Lösungshinweise zu Aufgabenblatt 4
1. (a) Sind beide Inputfaktoren variabel, so ist die Kostenfunktion eines Unternehmens
durch C(y) = y 2 /2 gegeben. Die Angebotsfunktion eines Unternehmens ist s(p) =
p.1 Da es 20 solcher Unternehmen gibt, ist die Marktangebotsfunktion
S(p) = 20p.
Für den Wettbewerbspreis p∗ gilt D(p∗ ) = S(p∗ ). Also:
120 − 10p∗ = 20p∗ ⇒ p∗ = 4.
Die Wettbewerbsmenge kann dann aus der Marktangebotsfunktion oder der Marktnachfragefunktion als
q ∗ = S(p∗ ) = D(p∗ ) ⇒ q ∗ = 80
bestimmt werden. Der Gewinn eines Unternehmens im Wettbewerbsgleichgwicht
ist
π ∗ = p∗ · s(p∗ ) − C(s(p∗ )) = 4 · 4 − 42 /2 = 8.
√
(b) Die hier relevante kurzfristige Produktionsfunktion ist f (x1 , 4) = 2 + x1 .2 Die
3
kurzfristige Kostenfunktion ist
4
für y ≤ 2
Ck (y) =
4 + 2(y − 2)2 für y > 2.
Entsprechend ergibt sich für die kurzfristige Angebotsfunktion eines Unternehmens:
p
sk (p) = + 2.
4
Die kurzfristige Marktangebotsfunktion ist daher
Sk (p) = 5 · p + 40.
In der kurzen Frist steigt der Wettbewerbspreis somit auf p∗k = 16/3, da
Sk (p∗k ) = D(p∗k ) ⇒ 15 · p∗k = 80.
Die Wettbewerbsmenge fällt auf qk∗ = Sk (p∗k ) = D(p∗k ) = 200/3.
In dem kurzfristigen Wettbewerbsgleichgewicht verkauft jedes Unternehmen 10/3
Einheiten Output zum Preis 16/3 und erzielt somit einen Erlös von 160/9. Die
Kosten sind Ck (10/3) = 68/9 und der Gewinn somit πk∗ = 92/9.
Beachte, dass der Gleichgewichtsgewinn eines jeden Unternehmens trotz Erhöhung
des Faktorpreises im Vergleich zur Ausgangssituation gestiegen ist.
1 Vgl.
Aufgaben 8 (c) und 11 (a) von Aufgabenblatt 3.
Aufgabe 11 (b) von Aufgabenblatt 2.
3 Die Herleitung entspricht der in Aufgabe 11 (c) von Aufgabenblatt 3. Da nun w = 2 (anstatt w = 1)
1
1
gilt, verdoppeln sich die variablen Kosten im Vergleich zu der in Aufgabenblatt 3 betrachteten Situation.
2 Siehe
1
In der langen Frist ist die Kostenfunktion eines Unternehmens bei den Inputpreisen (w1 , w2 ) = (2, 1) durch
2
Cl (y) = y 2
3
gegeben. Die Grenzkostenfunktion ist
Cl0 (y) =
4
y.
3
Da diese Grenzkostenfunktion streng steigend ist, ist die neue langfristige Angebotsfunktion eines Unternehmens
sl (p) =
3
p.
4
Die neue langfristige Marktangebotsfunktion ist
Sl (p) = 15p.
Abbildung 1: Grafische Darstellung zu Aufgabe 1: Die Marktangebotsfunktion in der Ausgangssituation ist blau dargestellt; der Wettbewerbspreis ist 4, die Wettbewerbsmenge ist 80.
Die kurzfristige Marktangebotsfunktion nach Erhöhung des Inputpreises ist grün dargestellt;
die langfristige Marktangebotsfunktion nach Erhöhung des Inputpreises ist lila.
Setzt man Marktangebot und Marktnachfrage gleich, erhält man den neuen langfristigen Wettbewerbspreis p∗l = 24/5. Beachte, dass p∗k > p∗l > p∗ , d.h. die
langfristige Reaktion des Wettbewerbspreises ist weniger stark als die kurzfristige Reaktion. In beiden Fällen steigt der Wettbewerbspreis.
Die langfristige Wettbewerbsmenge nach Änderung des Faktorpreises ist ql∗ =
Sl (p∗l ) = D(p∗l ) = 72. Die langfristige Reaktion der Wettbewerbsmenge ist also
weniger stark als die kurzfristige Reaktion.
2
Der Gewinn eines Unternehmens in dem langfristigen Wettbewerbsgleichgewicht
nach Änderung des Inputpreises bestimmt sich wie folgt: Jedes Unternehmen verkauft nun 18/5 Outputeinheiten zu einem Preis von 24/5. Der resultierende Erlös
ist 432/25. Die Kosten sind 216/25. Der Gewinn ist also πl∗ = 216/25. Der Gewinn
im langfristigen Wettbewerbsgleichgewicht nach Änderung des Faktorpreises liegt
also unterhalb des Gewinns im entsprechenden kurzfristigen Wettbewerbsgleichgewicht, aber immer noch oberhalb des Gewinns aus der Ausgangssituation.
2. Das Unternehmen sollte in den Markt eintreten, wenn sich dadurch ein Gewinn erzielen lässt. Ob dies der Fall ist, lässt sich wie folgt überprüfen: Man unterstellt zunächst,
das Unternehmen tritt in den Markt ein und bestimmt die in diesem Fall gewinnmaxierende Outputmenge und den resultierenden Gewinn. Ist dieser positiv, sollte das
Unternehmen eintreten. Ist der Gewinn negativ, sollte das Unternehmen dem Markt
fern bleiben.
Die Grenzkostenfunktion des aktiven Unternehmens ist durch M C(y) = 40 + 100y
gegeben und verläuft damit steigend. Ist das Unternehmen in den Markt eingetreten, ist die gewinnmaxierende Outputmenge also durch die Bedingung p = 40 + 100y
bestimmt. Mit p = 140 folgt hieraus y = 1. Der Gewinn bei dieser Outputmenge ist
140 − F − C(1) = 140 − 80 − 90 = −30
und somit negativ. Also sollte das Unternehmen nicht in den Markt eintreten.
Alternativer Lösungsansatz: Bestimme die minimalen Durchschnittskosten und
vergleiche sie mit dem Preis. Sind die minimalen Durchschnittskosten kleiner als der
Preis, sollte das Unternehmen eintreten. Anderenfalls sollte es inaktiv bleiben. Zur Bestimmung der minimalen Durchschnittskosten ist zunächst die effiziente Betriebsgrösse
ŷ zu bestimmen. Diese ist hier durch die Lösung des Problems
min AC(y) =
y≥0
80
+ 40 + 50y
y
gegeben. Die Bedingung erster Ordnung lautet:4
−
√
80
+ 50 = 0 ⇒ ŷ = 1.6.
2
ŷ
Die minimalen Durchschnittskosten sind also
√
80
AC(ŷ) = √
+ 40 + 50 1.6 ≈ 166.5
1.6
und liegen damit oberhalb des Preis p = 140. Wie zuvor ist die Schlussfolgerung, dass
das Unternehmen inaktiv bleiben sollte.
3. (a) Die Grenzkostenfunktion eines aktiven Unternehmens ist
M C(y) = 100 + 8y,
4 Anstatt
die Bedingung erster Ordnung herzuleiten, kann man auch direkt die Tatsache benutzen, dass die
effiziente Betriebsgrösse im Schnittpunkt von Grenzkostenfunktion und Durchschnittskostenfunktion liegt,
also durch die Gleichung
80
M C(ŷ) = AC(ŷ) ⇔ 100y =
+ 50y
y
gegeben ist.
3
Abbildung 2: Marktnachfragefunktion und kurzfristige Marktangebotsfunktionen für m =
20, m = 50 und m = 100 zu Aufgabe 3 (a). Kurzfristiger Wettbewerbspreis und Wettbewerbsmenge liegen in dem jeweiligen Schnittpunkt der kurzfristigen Marktangebotsfunktionen mit der Marktnachfragefunktion.
verläuft also streng steigend. Die Angebotsfunktion eines aktiven Unternehmens
ist also durch
0
für p < 100
s(p) =
(p − 100)/8 für p ≥ 100.
gegeben. Sind m Unternehmen im Markt aktiv, so ist die Marktangebotsfunktion
für p ≥ 100 also durch
p − 100
Sm (p) = m
8
gegeben. Für p < 100 ist das Marktangebot gleich Null.
Der kurzfristige Wettbewerbspreis p∗m ist durch die Bedingung D(p∗m ) = Sm (p∗m )
bestimmt. Hier gilt also
1000 − p∗m = m
p∗m − 100
8000 + 100m
⇒ p∗m =
8
m+8
mit entsprechender Wettbewerbsmenge
∗
qm
= D(p∗m ) = 1000 − p∗m =
900m
.
m+8
(b) Um die Anzahl der Unternehmen zu bestimmen, die in einem langfristigen Wettbewerbsgleichgewicht aktiv sind, ist zuerst der langfristige Wettbewerbspreis zu
4
Abbildung 3: Zu Aufgabe 3 (b): Der kurzfristige Wettbewerbspreis als Funktion der Anzahl
der aktiven Unternehmen in Relation zu den minimalen Durchschnittskosten: Für m <
172 liegt der Wettbewerbspreis oberhalb von min AC(y), so dass die aktiven Unternehmen
streng positive Gewinne erzielen und sich der Marktzutritt für inaktive Unternehmen lohnt.
Für m > 172 liegt der Wettbewerbspreis unterhalb von min AC(y), so dass die aktiven
Unternehmen Verluste erleiden und sich daher der Marktaustritt lohnt.
bestimmen. Dieser ist durch das Minimum der Durchschnittskosten gegeben. Das
entsprechende Minimierungsproblem5 ist
min
y>0
100
+ 100 + 4y
y
mit Bedingung erster Ordnung
−
100
+ 4 = 0 ⇒ 4y 2 = 100 ⇒ y = 5.
y2
Die Menge, bei der die Durchschnittskosten minimiert werden, ist also ŷ = 5.
Setzt man diese Menge in die Durchschnittskostenfunktion ein, erhält man den
langfristigen Wettbewerbspreis:
p∗ =
100
+ 100 + 4 · 5 = 140.
5
Die Marktnachfrage zu diesem Preis bestimmt die langfristige Wettbewerbsmenge
als q ∗ = D(140) = 860. Da jedes Unternehmen im Markt zu diesem Preis die
5 Anstatt dieses Minimierungsproblem aufzustellen, kann man auch Grenzkosten und Durchschnittskosten
gleichsetzen und nach y auflösen. Da sich Grenzkostenfunktion und Durchschnittskostenfunktion in dem
Minimum der Durchschnittskostenfunktion schneiden, wird durch diese Vorgehensweise ebenso das Minimum
der Durchschnittskostenfunktion bestimmt.
5
Menge ŷ = s(140) = 5 anbietet und im Gleichgewicht die angebotene Menge mit
der nachgefragten Menge übereinstimmt, muss
860 = m∗ 5 ⇒ m∗ = 172
gelten. Die Anzahl der Unternehmen, die in einem langfristigen Wettbewerbsgleichgewicht in diesem Markt aktiv sind, ist also 172.
4. Ist das Angebot fix, so lässt die Einführung einer Mengensteuer die aggregierten Handelsgewinne unverändert. Die aggregierte Konsumentenrente bleibt unverändert, da
der Gleichgewichtspreis, den die Konsumenten zu zahlen haben, unverändert bleibt.
Die aggregierte Produzentenrente fällt genau um den Betrag der Steuereinnahmen.
5. (a) Der Wettbewerbspreis ist durch die Bedingung D(p∗ ) = S(p∗ ) bestimmt. Hier
also:
100 − p∗ = 3p∗ ⇒ p∗ = 25.
Die Wettbewerbsmenge ist die Menge, die zum Wettbewerbspreis sowohl nachgefragt wie angeboten wird, q ∗ = D(p∗ ) = S(p∗ ). Hier also
q ∗ = 75.
Abbildung 4: Wettbewerbspreis, Wettbewerbsmenge und aggregierter Handelsgewinne (als
Summe von aggregierter Konsumentenrente und aggregierter Produzentenrente beim Wettbewerbspreis) zu Aufgabe 5 (a).
Die aggregierten Handelsgewinne in einem Wettbewerbsgleichgewicht entsprechen
der Summe aus aggregierter Konsumentenrente und aggregierter Produzentenrente zum Wettbewerbspreis und damit der Fläche zwischen der inversen Marktnachfragefunktion und der inversen Marktangebotsfunktion bis zur Menge q ∗ . Diese
6
Flächen kann man für den hier betrachteten Fall linearer Marktnachfrage und
-angebotsfunktionen wie folgt bestimmen (und so werden wir in den folgenden
Teilaufgaben verfahren): Die aggregierte Konsumentenrente bei p∗ = 25 ist ein
rechtwinkliges Dreieck mit Höhe 75 und Länge 75, so dass
KR∗ = 75 · 75/2
gilt. Die aggregierte Produzentenrente bei p∗ = 25 ist ein rechtwinkliges Dreieck
mit Höhe 25 und und Länge 75, so dass
P R∗ = 75 · 25/2
gilt. Addiert man die beiden Ausdrücke erhält man
HG∗ = 75 · 100/2 = 3750.
Hinweis: Allgemein kann man die aggregierten Handelsgewinne in einem Wettbewerbsgleichgewicht wie folgt schreiben:
Z q∗
HG∗ =
[PD (q) − PS (q)]dq.
0
Die inverse Marktangebotsfunktion ist hier
PS (q) = q/3,
die inverse Marktnachfragefunktion ist
PD (q) = 100 − q.
Also gilt hier
Z
HG∗ =
q∗
[100 − 4q/3]dq = 100q ∗ − 2(q ∗ )2 /3 = 7500 − 150 · 25 = 3750,
0
was mit dem Ergebnis der obigen Dreiecksflächenberechnungen übereinstimmt.
(b) Beim Preis p = 30 werden S(30) = 90 Einheiten angeboten und D(30) = 70 Einheiten nachgefragt. Der Staat muss also 20 Einheiten zum Preis von 30 aufkaufen.
Die resultierenden Ausgaben sind 600.
Die aggregierte Produzentenrente ist
P R(30) = 30 · 90/2 = 1350.
Die aggregierte Konsumentenrente ist
KR(30) = 70 · 70/2 = 2450.
Die Staatsausgaben wurden bereits als 600 bestimmt, so dass die aggregierten
Handelsgewinne
HG = 1350 + 2450 − 600 = 3200
betragen. Im Vergleich zum Wettbewerbsgleichgewicht werden die aggregierten
Handelsgewinne also um 550 Einheiten reduziert. (Anders gesagt: Die staatlichen
Ausgaben in Höhe von 600 erhöhen die Summe von aggregierter Konsumentenund Produzentenrente lediglich um 50 Einheiten.)
7
Abbildung 5: Angebotene und nachgefragte Menge bei p = 30 und die resultierenden Staatsausgaben (schraffierte Fläche) zu Aufgabe 5 (b).
(c) Der gesuchte Preis ist p̃ = 10, da hier D(p̃) = S(30) = 90 gilt. Der Staat kauft
also 90 Einheiten zum Preis von 30 auf und verkauft sie anschliessend zum Preis
p = 10, so dass Ausgaben in der Höhe von 90 · [30 − 10] = 1800 entstehen. Wie in
Teilaufgabe (b) beträgt die aggregierte Produzentenrente 1350. Die aggregierte
Konsumentenrente ist nun
KR(10) = 90 · 90/2 = 4050.
Die Staatsausgaben wurden bereits als 1800 bestimmt, so dass die aggregierten
Handelsgewinne
HG = 1350 + 4050 − 1800 = 3600
betragen. Im Vergleich zum Wettbewerbsgleichgewicht werden die aggregierten
Handelsgewinne also um 150 Einheiten reduziert - die Handelsgewinne sind jedoch
um 400 Einheiten höher als in der Situation aus Teilaufgabe (b).
(d) Die in der vorhergehenden Teilaufgabe beschriebene Situation entspricht dem
Fall, in dem eine Mengensubvention von 20 Geldeinheiten gezahlt wird. Nicht nur
die aggregierte Produzentenrente, sondern auch aggregierte Konsumentenrente
und staatliche Subventionszahlung stimmen mit den Werten aus der vorhergehenden Teilaufgabe überein. Insbesonder betragen die aggregierten Handelsgewinne
HG = 3600.
6. (a) Es handelt sich um eine Cobb-Douglas-Nutzenfunktion mit c = d = 1/2, so dass
die Nachfragefunktion durch
f1 (p1 , p2 , m) =
m
m
und f2 (p1 , p2 , m) =
2p1
2p2
8
Abbildung 6: Grafische Darstellung zu Aufgabe 5 (c): Bei p̃ = 10 entspricht die nachgefragte
Menge der zum Preis p = 30 angebotenen Menge. Die Staatsausgaben entsprechen der
schraffierten Fläche.
gegeben ist. Die indirekte Nutzenfunktion ist damit
r
U (p1 , p2 , m) = u(f1 (p1 , p2 , m), f2 (p1 , p2 , m)) =
m
2p1
r
m
m
= √
2p2
2 p1 p2
(b) Die Hicks-Kompensation der Preisänderung ergibt sich als Lösung der Gleichung
U (4, 1, 100) = U (1, 1, 100 + ∆m).
Also:
25 =
100 + ∆m
⇒ ∆m = −50.
2
(c) Die Hicks-Kompensation dieser Preisänderung ergibt sich als Lösung der Gleichung
U (1, 1, 100) = U (4, 1, 100 + ∆m).
Also:
100 + ∆m
= 50 ⇒ ∆m = 100.
4
Anmerkung: Berechnet man die “Konsumentenrente” der Preisänderung als die
Fläche links von der partiellen Nachfragekurve von Gut 1 zwischen den Preisen
p1 = 4 und p01 = 1 erhält man einen Wert, der zwischen dem Absolutwert der
beiden Hicks-Kompensationen liegt:
Z 4
50
= 50 ln 4 ≈ 70.
1 p1
9
7. Der Konsumentin geht es im Jahr 2008 besser, da das Güterbündel, welches sie im
Jahr 2007 nachgefragt hat, zu den Preisen des Jahres 2008 erschwinglich ist:
pt1 xb1 + pt2 xb2 = 6 · 20 + 30 · 30 = 1020 = mt .
8. Der Konsument wird durch die Kopfsubvention besser gestellt.
In der Ausgangssituation ohne jede Subventionen seien die Preise der beiden Güter
durch (p1 , 1) gegeben; das Einkommen des Konsumenten sei m.
Sei (x∗1 , x∗2 ) das Güterbündel, welches der Konsument bei einer Mengensubvention von
s = −t > 0 pro Einheit von Gut 1 nachfragt. Für dieses Güterbündel gilt
(p1 − s)x∗1 + x∗2 = m ⇔ p1 x∗1 + x∗2 = m + sx∗1 ,
wobei sx∗1 die Subventionszahlung ist, die der Konsument erhält.
Wird statt der Mengensubvention die Kopfsubvention S = sx∗1 gezahlt, so gilt
p1 x∗1 + x∗2 = m + S,
so dass das Güterbündel (x∗1 , x∗2 ) bei Zahlung dieser Kopfsubvention erschwinglich ist.
Hieraus folgt
U (p1 − s, 1, m) ≤ U (p1 , 1, m + S),
d.h. der Konsument wird durch die Kopfsubvention besser gestellt. Dieses wird durch
Abbildung 7 verdeutlicht.
10
Abbildung 7: Die Budgetgerade mit Kopfsubvention verläuft durch das Güterbündel (x∗1 , x∗2 )
(rot markiert), welches der Konsument in der Situation mit Mengensubvention wählt. Dieses
garantiert, dass der Konsument sich bei der Kopfsubvention zumindest gleich gut wie in
der Situation mit Mengensubvention stellt. Im Regelfall wird sich der Konsument streng
besser stellen, da er auf Grund des Substitutionseffekts bei der Kopfsubvention ein anderes
Güterbündel (hier pink markiert) wählt.
11