physik3_Demokritov_Vorlesung 3

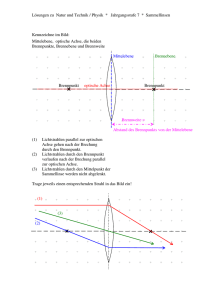
An welche Stichwörter von der letzten Vorlesung
können Sie sich noch erinnern?
Polarization
I = I 0 cos2 θ
Brewster-Winkel
θ B = arctan
n2
n1
Reelles Bild, virtuelles Bild
i = −p
1 1
31.3 Kugelspiegel, die Spiegelgleichung
Genau genommen ist ein ebener Spiegel ein Kugelspiegel mit einem unendlich großen
Krümmungsradius.
Konkaver Spiegel (Hohlspiegel)- der Krümmungsmittelpunkt C (der Mittelpunkt der Kugel)
befindet sich vor dem Spiegel.
1. Das Bildfeld (der abgebildete Teil der Umgebung) ist im
Vergleich zum ebenen Spiegel kleiner geworden.
2. Die Abbildung entsteht weiter hinten,
|i |>|p|
3. Es entsteht eine vergrößerte Abbildung.
Konvexer Spiegel (Wölbspiegel )- der Krümmungsmittelpunkt C
befindet sich hinter dem Spiegel.
1. Das Bildfeld wird größer.
2. Das Bild rückt näher an den Spiegel heran:
|i |<|p|
3.Das Bild ist kleiner als das Original.
Ein Objekt befindet sich unendlich weit von einem Kugelspiegel
entfernt auf dessen optischer Achse.
Das Licht, das von diesem Objekt ausgeht besteht aus den Strahlen,
die kleine Winkel mit der Hauptachse bilden (paraxiale Strahlen).
Die zugehörigen Lichtstrahlen verlaufen in diesem Fall
sämtlich parallel. In der Umgebung der optischen
Achse werden sie durch einen gemeinsamen Punkt F
reflektiert. Damit entsteht eine punktförmige
Abbildung des unendlich weit entfernten Objekts.
F ist der Brennpunkt des Spiegels, sein Abstand vom
Mittelpunkt c des Spiegels ist die Brennweite f:
AB = AF × 2θ = AC × θ
r
f =
2
Man bezeichnet den wirklichen Brennpunkt
des konkaven Spiegels als reellen Brennpunkt,
den wahrgenommenen Brennpunkt des
konvexen Spiegels als virtuellen Brennpunkt.
Außerdem vereinbart man die Brennweite f
des konkaven Spiegels als positive, diejenige
des konvexen Spiegels als negative Größe.
Wir suchen den Zusammenhang zwischen der Bildweite i und der Objektweite p für
konkave und konvexe Spiegel.
Reelle Bilder (p>f) entstehen auf der Seite des Spiegels, wo sich auch das Objekt befindet;
virtuelle Bilder (p<f) entstehen auf der anderen Seite.
N.B. Wir haben angenommen, dass das gleiche Ergebnis auch für alle anderen Strahlen gilt.
Das ist aber Wahr nur für paraxiale Strahlen (θ<<1). Die Näherung ist umso schlechter und
das Bild umso verschwommener, je stärker der Spiegel gekrümmt ist.
Dieser „Defekt“ sphärischer Spiegel wird als sphärische Aberration bezeichnet.
Ein Parabolspiegel dagegen reflektiert die Strahlen in einen perfekten Brennpunkt.
Um den Bildpunkt eines Objekts zu einem beliebigen, außerhalb der Achse liegenden
Objektpunkt zu finden, zeichnen wir ein Strahlenverlaufsdiagramm.
Hauptstrahlen:
1. Parallelstrahlen fallen parallel zur optischen Achse ein und werden durch den Brennpunkt
F reflektiert.
2. Brennpunktstrahlen verlaufen beim Einfall durch den Brennpunkt und werden parallel zur
optischen Achse reflektiert.
3. Mittelpunktstrahlen verlaufen durch den Krümmungsmittelpunkt und werden in sich
selbst reflektiert.
4. Scheitelpunktstrahlen treffen im Scheitelpunkt (Schnittpunkt c zwischen Spiegel und
Achse) auf und werden symmetrisch bezüglich der optischen Achse reflektiert.
Die Größe eines Objekts oder Bildes, senkrecht zur
optischen Achse gemessen, wird als Höhe bezeichnet.
h
Ist h die Höhe des Objekts (ab) und h'‚ (de) die Höhe
h′
des Bildes, so nennt man das Verhältnis h'/h = m die
Lateralvergrößerung (oder den Abbildungsmaßstab)
de
dc
i
m
=
−
=
−
=
−
des Spiegels. Vereinbarungsgemäß ist die Lateral
ab
ac
p
Vergrößerung positiv, wenn die Orientierung des
Bildes der des Objekts entspricht, und negativ, wenn
das Bild im Vergleich zum Objekt umgekehrt
erscheint. Aus dem Verlauf des 4. Strahls:
i
m= −
p
Die Dreiecke OO‘F und FBK sind ähnlich, deshalb:
p 
1
h OF
p− f
p
=
− = =
−
=
−  − 1 =
−
m
h′ FA
f
i
 f

Dividieren durch p: 1 1 1
1 1 1
− =
+ =
f p i
p i f
h
h′
K
p
i
Das ist die Speigelgleichung. Wenn man die Vorzeichenkonventionen folgt
(positiv/negativ i und positiv/negativ f), gilt die Speigelgleichung für alle mögliche
Konfigurationen.
31.4 Abbildungen durch Brechung auf ebenen Flächen
Das Snellius’sche Brechungsgesetz (Luft)
sin θ1 = n2 sin θ 2
Wie tief sehen wir ein Objekt unter Wasser?
x
= tan θ1 ≈ sin θ1
d′
x
= tan θ 2 ≈ sin θ 2
d
d ′ sin θ 2 1
= =
d sin θ1 n2
Wasser: n2= 1.33 d‘=0.75 m
sin θ B = n sin θ A
O
A
B
d
∆ OB − OA
OA
=
= sin θ B − sin θ A
= tan θ A ≈ sin θ A
d
d
d
 1
OB
d
θ
sin
=
∆
B 1 −

= tan θ B ≈ sin θ B
n


d
Die Richtung des Lichtstrahls bleibt insgesamt beim Durchgang
durch eine ebene Scheibe unverändert. Dies gilt für beliebige
Einfallswinkel. Allerdings wird der Strahl etwas verschoben.
Doppelbrechung: es gibt auch Systeme, in denen der Brechungsindex von der
Lichtpolarisation (d.h. der Orientierung der elektrischen Feldkomponente E) des
eingestrahlten Lichtes abhängig ist. Man bezeichnet solche Medien als optisch anisotrop.
Optische Anisotropie kommt in häufig in den Kristallen vor. Bsp.: der
Kalkspat (Calcit, Calciumkarbonat, СаСОз) - ein Kristall mit hexagonaler
Symmetrie. In solchen Kristallen existiert eine hochsymmetrische-Achse die optische Achse des uniaxialen Kristalls. Fällt das Licht parallel zur
optischen Achse des Kristalls ein, breitet sich dieses Licht in dem Kristall
gleichförmig aus, d.h. unabhängig von seiner Polarisation (der ordentliche
Strahl, no=1,66).
Dem außerordentliche Strahl (senkrecht zur optischen Achse) kann seinen
E-Vektor parallel zur optischen Achse (na = 1.5) haben.
Ein unpolarisierter Lichtstrahl wird auf einen
Calcitoberfläche in zwei Teilstrahlenaufgespalten, den
ordentlichen und den außerordenlichen Strahl, die
senkrecht zueinander polarisiert sind. Es kommt auch zu
einer räumlichen Trennung. Man sieht daher durch
einen Kalkspat das sich darunter befindende Bild doppelt
(Doppelbrechung).
Propagiert das Licht senkrecht zur optischen Achse des Kalkspats, dann breiten sich
ordentlicher und außerordentlicher Strahl zwar in die gleiche Richtung aus, aber mit
unterschiedlichen Geschwindigkeiten. Es kommt daher bei dem austretenden Strahl zu
einer Phasendifferenz zwischen den verschiedenen Polarisationskomponenten, die von
der Kristalldicke und der Wellenlänge des Lichts abhängt.
Die relative Phase ϕ bestimmt die Polarisation der Welle.
Eingang:



E ( z, t ) =
E0, x ex + E0,y e y cos ( kz − ωt )
ϕ=0
(
)
Wenn die Wellenlänge und die Kristalldicke so angepasst sind, dass

auf dem Ausgang


E
z
,
=
t
E
cos
kz
−
ω
t
e
−
sin
kz
−
ω
t
e
(
)
(
)
(
)
x
y
ϕ=π/2
kann man eine linear polarisierte Welle in einer zirkular polarisierten
Welle umwandeln und umgekehrt.
(
)
31.5 Sphärische brechende Flächen
d
p
i
Betrachten wir die Brechung von Strahlen an der sphärischen Oberfläche eines
transparenten Mediums (n2>n1). Beispiele: Linse, Hornhaut des Auges.
Wir wollen zeigen, dass alle vom Punkt O des Objektes ausgehenden Strahlen in einem
gemeinsamen Bildpunkt I, fokussiert werden (paraxiale Strahlen!).
n1θ1 = n2θ 2
Nach dem Snellius’schen Gesetz gilt: n1 sin θ1 = n2 sin θ 2
Aus dem OPC: θ1= α + β , aus dem PCI β= θ 2 + γ
n1θ1 = n2θ 2
n1 (α + β )= n2 ( β − γ )
d
d
d
=
α =
γ
=
β
p
i
r
n1 n2 n2 − n1
+ =
p i
r
n1α + n2γ = β ( n2 − n1 )
Wir sehen, dass die Bildweite i nicht
vom Winkel des Strahls (α) abhängt.
n1 < n2
n1 n2 n2 − n1
+ =
p i
r
Die Gleichung gilt für alle Fälle – wenn wir
die folgenden Konventionen vereinbaren:
1. Wenn die Oberfläche konvex ist (d. h. wenn sich der
Krümmungsmittelpunkt C hinter der Fläche befindet, die der Fläche
gegenüber liegt, von der das Licht kommt), dann ist r positiv; ist die
Oberfläche konkav (C liegt auf der Seite, von der das Licht kommt),
dann ist r negativ.
r>0 i>0
r<0 i<0
2. Für die Bildweite i gilt die gleiche Konvention: Sie ist positiv auf der Seite,
die derjenigen gegenüberliegt, von der das Licht kommt, und negativ auf der gleichen Seite.
3. Die Objektweite p ist positiv auf der Seite, von der das Licht kommt und andernfalls
negativ.
Die Gleichung gilt auch für den Fall
n1 > n2
n1 > n2