4. Schulaufgabe aus der Mathematik * Klasse 9c - Rasch-Web

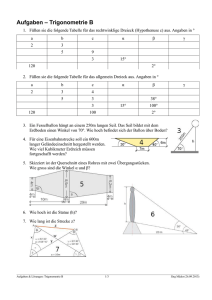
4. Schulaufgabe aus der Mathematik * Klasse 9c * 14.06.2012 * Gruppe A
1. Im Bild sind die beiden Geraden mit den Funktionsgleichungen
f (x)  0,8  x  2 und g(x)  1,5  x  1 dargestellt.
a) Unter welchem Winkel schneiden die beiden Geraden
jeweils die x-Achse? Runde auf 0,1o genau.
b) Unter welchem Winkel schneiden sich die beiden Geraden?
2. Das Bild zeigt die beiden rechtwinkligen Dreiecke ABC und TOR.
b) Im Dreieck TOR gilt x = 5 und   40o .
Berechne die Seitenlänge y und den
Flächeninhalt F∆TOR des Dreiecks.
a) Im Dreieck ABC gilt b = 7
und c = 9 . Berechne die Seitenlänge a und den Winkel ß !
T
C

FTOR = ?
=?
 = 40

R
B
A
o
O
Alle Bilder sind nicht maßstabsgetreu!
3. Ein Quader hat die Kantenlängen a = 6,0 cm ,
b = 4,0 cm und c = 3,0 cm . Die beiden
eingezeichneten Raumdiagonalen scheiden
sich unter dem Winkel  .
d
c = 3 cm

a) Zeichne sauber ein Schrägbild mit
dem Verzerrungswinkel 45o und dem
Verkürzungsfaktor q  0,5  2
a = 6 cm
b) Berechne die Länge d einer Raumdiagonale und den Winkel  auf 0,1o genau.
S
4. Eine gerade Pyramide ABCDS hat als Grundfläche ein
Quadrat mit der Kantenlänge a = 6 und die Höhe h = 5.
k
a) Berechne die Kantenlänge k der Pyramide.
[Ergebnis: k  43 ]
h=5
D
C
a
b) Berechne den Oberflächeninhalt der Pyramide.
A
a=6
Aufgabe
1a
b
2a
b
3a
b
4a
b
Summe
Punkte
3
2
3
4
3
5
2
4
26
B
Gutes Gelingen! G.R.
4. Schulaufgabe aus der Mathematik * Klasse 9c * 14.06.2012 * Gruppe B
1. Im Bild sind die beiden Geraden mit den Funktionsgleichungen
f (x)  0,7  x  1 und g(x)  1,5  x  2 dargestellt.
a) Unter welchem Winkel schneiden die beiden Geraden
jeweils die x-Achse? Runde auf 0,1o genau.
b) Unter welchem Winkel schneiden sich die beiden Geraden?
2. Das Bild zeigt die beiden rechtwinkligen Dreiecke ABC und TOR.
b) Im Dreieck TOR gilt x = 4 und   40o .
Berechne die Seitenlänge y und den
Flächeninhalt F∆TOR des Dreiecks.
a) Im Dreieck ABC gilt b = 6
und c = 7 . Berechne die Seitenlänge a und den Winkel ß !
T
C

FTOR = ?
=?
 = 40

R
B
A
o
O
Alle Bilder sind nicht maßstabsgetreu!
3. Ein Quader hat die Kantenlängen a = 8,0 cm ,
b = 4,0 cm und c = 3,0 cm . Die beiden
eingezeichneten Raumdiagonalen scheiden
sich unter dem Winkel  .
d
c = 3 cm

a) Zeichne sauber ein Schrägbild mit
dem Verzerrungswinkel 45o und dem
Verkürzungsfaktor q  0,5  2
a = 8 cm
b) Berechne die Länge d einer Raumdiagonale und den Winkel  auf 0,1o genau.
S
4. Eine gerade Pyramide ABCDS hat als Grundfläche ein
Quadrat mit der Kantenlänge a = 8 und die Höhe h = 6.
k
a) Berechne die Kantenlänge k der Pyramide.
[Ergebnis: k  2  17 ]
h=6
D
C
a
b) Berechne den Oberflächeninhalt der Pyramide.
A
a=8
Aufgabe
1a
b
2a
b
3a
b
4a
b
Summe
Punkte
3
2
3
4
3
5
2
4
26
B
Gutes Gelingen! G.R.
4. Schulaufgabe aus der Mathematik * Klasse 9c * 14.06.2012 * Gruppe A * Lösung
1. a) tan   0,8    tan 1 (0,8)  38,659...o  38,7o
tan   1,5    tan 1 (1,5)  56,309...o  56,3o
φ
b)      (Aussenwinkel) 
      56,309...o  38,659...o  17,650...  17,7o
α
ß
a 2  b2  c2  a 2  81  49  32 
2. a)
a  32  4  2 und
b)
sin  
b 7


c 9
7
  sin 1 ( )  51, 057...o  51,1o
9
sin  
x
y
 y
x
5

 7, 778...  7,8
sin  sin 40o
tan  
x
z
 z
x
5

 5,958...  5,96
tan  tan 40o
FTOR 
1
1
5
 x  z  5
 2,5  5,958...  14,89...  14,9
2
2
tan 40o
3. a)
d
c = 3 cm


x
a = 6 cm
x 2  a 2  c2  x 
b)
5
4. a)
6
7
11
  2   und tan  
b
4
   2  tan 1 (
)  61, 61...o  61, 6o
x
45
k
9
12
13
14
45cm2  16cm2 
61cm  7,8cm
S
2
1
1
 DB   2  a  3  2 und k 2  h 2  MB 
2
2
2
h 2  MB 
2
b)
10
45 cm  3 5 cm
d 2  x 2  b2  d 
MB 
8
36cm2  9cm2 x 
25  18 
k
h=5 x
43
a
k 2  x 2     x  43  9  34
2
1
FPyramide  a 2  4   a  x  62  2  6  34  36  12 34
2
D
A
C
M
a=6
a
B
4. Schulaufgabe aus der Mathematik * Klasse 9c * 14.06.2012 * Gruppe B * Lösung
1. a) tan   0,7    tan 1 (0,7)  34,992...o  35,0o
tan   1,5    tan 1 (1,5)  56,309...o  56,3o
φ
b)      (Aussenwinkel) 
      56,309...o  34,992...o  21,317...  21,3o
6
b 6

   sin 1 ( )  58,997...o  59,0o
7
c 7
x
4
 y

 6, 222...  6, 2
sin  sin 40o
a  13 und
b)
7
ß
a 2  b2  c2  a 2  49  36  13 
2. a)
y
α
sin  
sin  
x
y
tan  
x
z
FTOR 
1
1
4
 x z  4
 2  4, 767...  9,534...  9,5
2
2
tan 40o
 z
x
4

 4, 767...  4, 77
tan  tan 40o
3. a)
d
6
5

c = 3 cm

x
4
3
a = 8 cm
2
x
5
b)
6
7
8
9
10
11
14
15
16
64cm2  9cm2 
d 2  x 2  b2  d 
73cm2  16cm2 
MB 
k
73 cm 
73 cm
89 cm  9, 4cm
b
4
   2  tan 1 (
)  50,174...o  50, 2o
x
73
S
2
1
1
 DB   2  a  4  2 und k 2  h 2  MB 
2
2
2
h 2  MB 
2
b)
13
x 2  a 2  c2  x 
  2   und tan  
4. a)
12
36  32 
k
h=6 x
68  2  17
a
k 2  x 2     x  68  16  52  2  13
2
1
FPyramide  a 2  4   a  x  82  2  8  2  13  64  32 13
2
D
A
C
M
a=8
a
B