Inhaltsverzeichnis 1 Ähnliche Figuren

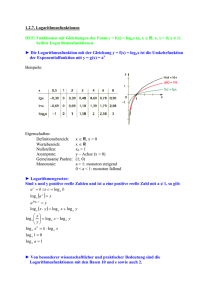
Herr Amrein: Mathematik Klasse 9··
Inhaltsverzeichnis
1 Ähnliche Figuren.................................................................................................................1
1.1Zentrische Streckungen................................................................................................1
1.2Ähnliche Dreiecke.........................................................................................................2
1.3Stahlensätze.................................................................................................................3
1.4Erweiterung der Strahlensätze.....................................................................................4
2Der Satz des Pythagoras.....................................................................................................5
2.1Beweis des SdP............................................................................................................5
2.2Pythagoras im Raum....................................................................................................6
2.3Der Sinus......................................................................................................................7
2.4Sinus, Kosinus und Tangens........................................................................................8
2.5Winkel- und Längenberechnungen...............................................................................9
3Potzenzen............................................................................................................................9
3.1Zehnerpotzenzen..........................................................................................................9
3.2Rechen mit Zehnerpotzenzen......................................................................................9
3.3Potenzen mit gleicher Basis.......................................................................................10
3.4Potenzen mit gleichem Exponenten...........................................................................11
3.5Potenzen mit rationalem Exponenten.........................................................................12
1
Ähnliche Figuren
Die beiden Fahrräder sind zueinander
„ähnlich“:
Drehungen und Vergrößerungen sind
erlaubt, doch Verzerrungen (die Winkel verändern
würden) sind verboten.
1.1 Zentrische Streckungen
Einführen: OHP-Zeichnung. Wo ist das
Licht auf der Bühne?
Merke:
Zeichne die Strecke von Streckzentrum S zu jedem Punkt P der Figur.
Den Steckfaktor k kann man sich als Vergrößerungsfaktor vorstellen.
Der Punkt P' liegt k-mal soweit von S entfernt wie P.
Figur und Bildfigur sind zueinander „ähnlich“
k=3
Beispiel:
Aufgabe:
S14 Nr.1a,b
S 14 Nr.2.a,b,c
Für schnelle Nr.2a) Nr.4
Haufgabe:
Steckung mit k=3/8
S 15 Nr. 3, 7
Aufgabe:
Zeichnen mit Zentischer
Aufgabe:
S 15 Nr. 5
Streckung.
S 16 Nr. 8
S 16 Nr. 9 Technische Beschreibung:
Gut: „Zunächst wird ein...“
Mittel: „Zunächst zeichnet man...“
Schlecht: „Zunächst zeichne ich...“
Arbeitsblatt: Zentrische Streckung
Aufgabe:
S 16. Kannst du noch.
1.2 Ähnliche Dreiecke
Mitbringen: Zirkel, Taschenrechner
Arbeitsblatt: Ähnliche Dreiecke
Merke:
F
C
Zwei Dreiecke sind zueinander ähnlich, wenn
...sie in drei Winkeln übereinstimmen (www)
E
D
...sie in drei Seitenverhältnissen übereinstimmen.A
B
..sie in einem Seitenverhältnis und einem passenden Winkel übereinstimmen
(sws oder SsW)
TIPP:
Enstprechende Längen/Winkle mit identischen Farben markieren
Theorie:
Die Dreiecke sind ähnlich.
Welche Streckenklängen sollte man dividieren, damit der Bruch 2/3 entsteht.
AC 2
DF 2
≈ und
≈
AB 3
DE 3
also
AB 5
EF 5
≈ und
≈
BC 2
DE 2
also
MN 4
NO 4
≈ und
≈
NL 5
OP 5
AC DF
=
AB DE
AB EF
=
BC DE
also
MN NO
=
NL OP
F
C
E
D
B
A
L
·
M
N
·
O
P
Stationen:
Längen in Dreicken
· C
Aufgabe:
E
·
A
B
D
Gegeben sind die Längen: AB=7cm, AC=6,5cm, AD=3,5cm
a)Konstruiere die Figur gemäß den Vorgaben
b)Wenn AE rot markiert werden und AD grün markiert werden, sollte was
noch markiert werden?
c)Stelle eine Gleichung auf:
d)Löse die Gleichung.
Aufgaben:
AC AD
=
AB AE
AC AD 6,5 3,5 7,5 AE 7,5
=
→
=
→
=
→ ⋅3,5= AE≈4,04
AB AE 7,5 AE 6,5 3,5 6,5
S18 Nr. 4
a)Welcher Ähnlichkeitssatz aus Merke-Kasten? → Drei gleiche Winkel, da
parallele Geraden
b)Skizze ins Heft, Farbig markieren, Bekanntes anschreiben
Finde eine Gleichung für CD (2,81) später für MC(4,69), dann ist AC
(2,19)logisch
α
90-α
S18 Nr. 5
I
Jedes Dreieck hat eine rechten
Winkel, den Winkel α und den
Winkel (90°-α) nach dem www-Satz sind sie ähnlich
HA:
II
Seite 18 Nr. 2 und 3
1.3 Stahlensätze
Bisher hatten wir die „Fingerabdrücke“ der
ähnlichen Dreiecke:
b
u / c = v /(c+d)
Wir ordnen nach Farben:
v
u
a
c
d
u / c = v /(c+d)
|(c+d)
u ∙(c+d) / c = v
| /u
(c+d) / c = v/u
Dieses Verhältnis von „den großen zu den kleinen Seiten“ beträgt ca. 1,3
Ein Drittes mal lässt sich dieser Wert erzeugen. Nämlich: (c+d) / c = v/u = (a+b)/a
Die „Strahlensätze“ bieten noch andere Möglichkeiten, Abschnitte (gleicher Farbe) in ins
richtige Verhältnis zu setzen:
Aufgabe:
a/b=?
c/(c+d)=?
d/c=?
evtl. noch mehr bei Problemen.
Mündlich:
Seite 20 Kasten lesen. Was Unterscheidet den ersten von dem 2ten Satz?
Antwort: Beim 2ten Strahlensatz sind die Parallelen beteiligt.
Aufgabe:
Seite 21 Nr.1 a) und b) Einfärben, je 5 Gleichungen
Beispiel:
1.
4/x=3/2
2.
(4+x)/4=5/3
3.
x/4=2/3
Welche stimmt? Alle
x
3
Welche ist gut? Nr3 x im Nenner
PAufgabe:
v
u
4
2
S21 Nr.2 c (erst x dann y) und d)
S22 Nr.3a
Haufgabe:
Kasten übertragen. Längen und Formeln einfärben
S21 Nr. 2a,b
S22 Nr.3b
Aufgabe:
Der Einbrecher (muss nochmal geprüft werden)
Aufgabe:
S21 Nr.4
Aufgabe:
Zeichne eine beschriftetes nicht maßstabsgetreues Strahlensatz-Problem,
dass zum folgenden Bruch passt
a)
a 2
=
3 5
b)
j+5 2+5
=
5
2
c)
h+2 2+0,5
=
h
0,5
d)
f +0,1 0,3
=
f
0,2
1.4 Erweiterung der Strahlensätze
Aufgabe:
a/b=
b)
a+b/b=
c)
d)
e)
c
d
b
v
a)
a
u
Ergänze die folgende Gleichungen
und finde drei weitere. Bist du dir
unsicher kannst du einfach
nachmessen, ob es stimmt, was du
aufgeschrieben hast.
Aufgabe:
Aufgabenblatt (Vernetzung Terme)
Aufgabe:
S25 Nr 2 a) b) und 3a)
Haufgabe:
S25 Nr 2 c) d) und 3b)
Aufgabe:
Seite 25 Nr. 5
2 Der Satz des Pythagoras
Einstieg:
Arbeitsblatt
Aufgabe:
Kasten S36 übertragen
Pythagoras
-Trippel:
345
435
5 12 13
6 8 10
7 24 25
8 6 10
8 15 17
9 12 15
10 24 26
12 5 13
12 9 15
12 16 20
15 8 17
15 20 25
16 12 20
20 15 25
20 21 29
21 20 29
24 7 25
24 10 26
S37 Nr. 1a) b) für schnelle c)
Mündlich:
S37 Nr. 2a)x=1 b)x=2 c)x=6 d)x=5
Theorie:
c
a=1,2
c=3
a
b=2,5
b=2,5
2)
a²+b²=c²
a²+b²=c²
|-b²
1,2²+2,5²=c²
a²=c²-b²
Fehlende Seite berechnen – Konstrucktion nach sss – Flächeninhalt
7,69=c²
|√
a²=3²+2,5²
a=3,2cm
c=_____
2,77≈c b=2,4cm
a²=2,75
|√
a=1,66
a=3cm
b=_____
c=5,2cm
3)
a=
4)
u= 2z
Aufgabe:
1)
Haufgabe:
√ 30
b=
√6
v=_____
c=_____
w=3z
mit 1z=1zoll=2,54cm
S 38 Nr.3
2.1 Beweis des SdP
Aufgabe:
S 38 Nr.4a,b
a
b
b
a
a
b
b
a
Aufgabe:
b
n
he
e
t
nts abc
e
t
t
a
ra mi
d
e
a k
Qu eiec
e r
elb e D
g
s lig
da ink
h
rc chtw
u
D re NEU:
c
b
a
a
b
Bilde die Summe aller Flächen im ersten und im zweiten Quadrat.
Vereinfache auch.
b
a
Erstes Quadrat:
a²+....
Zweites Quadrat:
1/2ab+1/2ab+...
Es gilt:
Erstes Quadrat
=Zweites Quadrat (mit rechtwinkligen Dreiecken)
a²+2ab+b²
=c²+2ab
DANN:
a²+b²
=c²
Haufgabe:
S38 Nr.4c)
|-2ab
S39 Nr. 11 12
Aufgabe:
Du kannst die Länge der Hypothenuse c nur mit Zahlen,x und y darstellen
c=_____
3
16y
x
3+x
b=(x-y)
√(2xy+y²)
c=_____
x
12y
c=_____
x
c=_____
c=(x+y)
Lösung:
a=___
a)
c² =9+ x² → c= √9+ x²
b)
c=20y
c)
c=√ 9+6x+ x² + x² =√ 9+6x+ 2x²
d)
c=√ x² + 2xy+ y² =√( x + y )2=x + y
e)
a² =c²−b² →a=√ c² −b²=√ ( x+ y) ²−( x− y) ²=√ x² + 2xy+ y² −x² + 2xy− y²=√ 4xy=2 √ xy
Aufgabe:
Al Capone´s Aktenkoffer ist 45cm lang und 35cm hoch. Der Lauf seiner
Maschinenpistole ist 55cm lang. (c=57cm → passt rein)
2.2 Pythagoras im Raum
Einführung
Mal ehrlich, jeder hasst es, wenn der Strohhalm in den
Saftkarton rutscht!
Schräg über die Verpackung einer 0,2l-Saftbox ist ein
Strohhalm geklebt.
a)Die Box ist 6cm lang und 4cm breit. Wie hoch ist die
Box? (1l=1000cm³). Schreibe die Größen dünn an die
Zeichnung (8,33cm)
d
d1
b)Schau auf die Zeichnung. Der Strohhalm hat die Länge
d1. Du kannst d1 mit dem SdP berechnen. Wie?
(d1=10,3cm)
c) Hätte der Strohhalm nicht die Länge d1 sondern mindestens d, könnte er nicht mehr in
den Karton rutschen...und erneut hilft Pythagoras. Wo ist hier das passende rechtwinklige
Dreieck. Markiere es farbig in der Zeichnung und berechne d (11cm)
Aufgabe:
S42 Nr.4
Aufgabe:
Das glschenkl. Dreieck hat die Grundseite a=5cm b=c=3cm.
a)Hilfslinie → rechtwkl Drk → SdP → Höhe und Fläche berechnen h=1,65cm
b)Zentrische Streckung mit k=√2. Neuer Flächeninhalt?
Aufgabe:
Quader1:
l=√7 b=√2 h=√3
Quader2:
l=4x b=2x h=2x
A
C
a)Berechne BC und dann AC (1:3und√12 2:√(20)x;√(24)x) B
b)Berechne die Fläche des „rechtwinkligen“ Dreiecks ABC (1:1,5√3 2:√(20)x²)
Klassenarbeit:
Zentrische Streckung Bist du sicher: Seite 15
Strahlensatz Bist du sicher: Seite 22 und 25
Pythagoras Bist du sicher: Seite 38 und
42
x
Seitenfläche
2.3 Der Sinus
Einstieg:
45°
Problem Ritter Eisenkopf
Arbeitsblatt: Dreiecke
S 45Nr. 1b
Aufgabe:
S 45 Nr. 1a,c, 2
x
Tafel:
Pyramide Ulm
Querschnitt
S 46 Nr. 5
29m
Haufgaben: S 45 Nr.
Aufgabe:
a)Berechne die Länge x in der Zentralbibliothek in Ulm. Dann die Höhe
(x=37,9m h=31,4m)
b)Berechne den Flächeninhalt der vier Glaswände (A=4*29*37,9/2=2198m²)
Aufgabe:
S 45 Nr. 6
2.4 Sinus, Kosinus und Tangens
α
te=3
e
h
t
a
Gegenkathete
Ank
=0,53
Ankathete
,6
th=1
α=28 °
α
1,6
ath=
G.k
α=28 °
α
Gegenkathete
=0,47
Hypothenuse
Hypo=3,4
3
ete=
h
t
a
Ankathete
Ank =0,88
Hypothenuse
Hypo=3,4
G.ka
Austeilen:
α=28 °
sin-1(0,47)
cos-1(0,88)
tan-1(0,53)
sin(28°)
cos(28°)
tan(28°)
Merke:
sin(α)=Gegenkathete/Hypothenuse
cos(α)=Ankathete/Hypthenuse
tan(α)=Gegenkathete/Ankathete
Mündlich:
S48 Nr.3a
Aufgaben:
S48 Nr.3b
S48Nr.1b dann a)
Haufgaben: S48Nr.2
Aufgabe:
Im Winter fährst du die schwarze Piste hinab. Diese hat 39° Steigung. Der
Fahrspaß dauert 3,4km lang. Auf einer Karte (von oben) wäre sie dagegen
nur ...km lang. (Skizze von der Seite) 2,64km
Wie lang ist die Strecke auf eine 1:50 000 Karte? 5,28cm
Aufgabe:
S 48 Nr. 4 und 49 Nr. 6
Bingo:
1
2
y=2x²-1
P(0|x)
9
3
4
5
6
7
8
a²+_ab+b² √√81
g=12
h=2/3
125/25
√(0,04)
*30
(-2-4)*(2)+(-1)-4
2³
10
11
12
13
14
15
16
ungerade;
Quersumme 2
y=x-2
y=-x+12
Summe
Punkt S
Unglücks y=(x-4)²
9885:659 XVI
zahl,
y=x-2
Primzahl x1+y1+x2
+y2
√27/√3*3 X
Aufgabe:
S49 Kannst du noch
,5°)
n(38
a
t
=
,5
x/26 ,9m
25m
x=21
38,5°
27,5m
2.5 Winkel- und Längenberechnungen
Aufgaben:
S51 Nr.2
°)
(38,5
n
a
t
,5 =
x/26 ,9m
x=21
8°
S52 Nr.3
a)1572m/30000m=5,25% bzw. tan-1(1572/30000)=3°
803/x=sin(3°)
x=803/sin(3°)=15,3km
c)1,3km+112m=1,41km Höhe
b)15,3km
25
3°
Aufgabe:
(915-112)m
3°
x/25=sin(3°)
x=25·sin(3°)=1,3
Die Stange eines Zeltes ist 1,80m hoch. 1m²Zeltstoff kostet 6,99€/m². Das
Zelt hat keine Bodenplane
x=1,8/tan(76°)+1,8/tan(40°)
3m
x=2,59m
z
y
40°
x
76°
y=1,8/cos(40°)=2,80
z=1,8/cos(76°)=1,85
A=1,8x+3y+3z=18,61m² → 130€
Wadi:
Lineare Funktionen Klasse 7 C3 und C4
3 Potzenzen
3.1 Zehnerpotzenzen
todo
3.2 Rechen mit Zehnerpotzenzen
Merke:
a·10x+b·10x=(a+b)·10x
Bsp: 3·107m-1,2·107m=1,8·107m
30000000-12000000=18000000
a·10x · b·10y=(a·b)·10x+y
Bsp 3·103m · 2·104=6·107m²
3000m·20000m=60000000m²
a·10x : b·10y=(a:b)·10x-y
Bsp 8·109m²: 2·104m=4·105m
800000000m²:20000m=400000m²
Aufgabe:
S 64 Nr.1a-d
S 65 Nr.2a-d Nr.4a-b Nr.6 a-b
HA:
Wahlweise:S 64 Nr.1e-f S 65 Nr2.e-f Wahlweise Nr.6c-d
Aufgabe
S 65 Nr. 7+ Berechne Maßstab
Bingo Funktionen: 9er-Bingo
x2
Wdh: Lösungsformel
Bisher y=blabla neu: f(x)=blabla
f(x)=ax²+bc+c für Nullstellen:
0=ax²+bx+c (die Null links ist nötig für Lösungsformel)
x 1=
1
−b+ √ b² −4ac
2a
x 2=
x1
−b−√ b² −4ac
2a
2
Anzahl der Nullstellen Wo
y=0,5(x-3)²
schneidet
y=x²-8x+12
erstmals xAchse?(x1
und x2
berechen)
3
4
5
Summe der
ScheitelKoordin.
y=2(x-4)²-1
Wie viele
Kleinster y-Wert
Kreuze kann von
man haben
y=0,5(x-2)²+5
ohne „Bingo“
6
7
8
9
X
Summe x1 und x2
Wenn 3=2x² - 12x +
20 (später GTR)
y=x²-17x+49 Alle vier
y = x² - 4x +4
P(__|0)
Schnittpunktko P(-1|?)
ordinaten
addieren:
f(x) = x²-4x + 2
f(x)=2
3.3 Potenzen mit gleicher Basis
Einführung:
M7
r²r³y ( X² )³mas schreibe die Buchstaben aus.
M6
Erinnerung:
10−3=
Merke:
a p⋅a q=a⋅...⋅a
⏟ a⋅...⋅a
⏟ =a p +q Beispiel: 23⋅24=2⋅2⋅2⋅2⋅2⋅2⋅2=27
1
1
=
3
10 1000
p mal
q mal
p−q
a p :a q =a⋅...⋅a
⏟ :(a⋅...⋅a)
⏟=a Beispiel: 32 :34=3⋅3:(3⋅3⋅3⋅3)= 19 = 12 =3−2
p mal
q mal
3
(a p )q =a⋅...⋅a
⏟ ... a⋅...⋅a
⏟ =a p⋅q
⏟
p mal
p mal
2 3
6
⏟ 5⋅5
⏟ 5⋅5
⏟=5
Beispiel: (5 ) =5⋅5
q mal
Aufgaben:
S67
Nr.1a-d)
Nr.2a-d)
Nr.4a-d)
Nr.5a-d)
Nr.9f-r)
HA:
Nr.1,2,4,5,9 jeweils Rest
Aufgaben:
S6710a-c
S67 Nr.12 (mit Papier vorführen)
S68 Nr.19 (hatte ich schon 1zu1 als Schüler im Buch)
10cm
Aufgabe:
Summiere den Flächeninhalt aller roten
Flächen A1 bis A13
Wie viel Prozent des Körpers ist rot?
A2
10cm
Summiere den Flächeninhalt aller grünen
Flächen A2 bis A14
A3
A4
Mit welcher Zweierpotenz kommt man
A5
A1
usw
A3 → A1 A1 → A3 A3 → A12?
3.4 Potenzen mit gleichem Exponenten
Einführung: Kinofilm „Inception“
LieferwagenLimbo
Im Flugzeug
Schnee-Welt
Im Hotel
Jagd
(Traum)4
(Wirklichkeit)
(Traum)³
(Traum)²
Traum
Traum (Traum) Traum
Traum
Es gilt: 5 Miuten Traum
1Stunde
a)Wie viel Zeit hat man in „Limbo“, wenn im Flugzeug 15 Minuten vergehen.
15Min*124=311040Min=216Tage
b)Der Lieferwagen stürzt von einer Brücke s=18m, wie viel Zeit bleibt in der
Schneewelt? Es gilt s= ½ g t² mit g=9,81 (Berechne zuerst die Fallzeit t)
tfall=√(2s/g)=1,92s → tSchneewelt=276s=4:35min
Merke:
p
p
a ⋅b =( a⋅b)
p
a p
p
p
a :b =( )
b
3
3
3
Beispiel: 4 ⋅2 =4⋅4⋅4⋅2⋅2⋅2=(4⋅2)⋅( 4⋅2)⋅(4⋅2)=(4⋅2)
4
4
Beispiel:2 : 3 =
Mündlich:
S 69 Nr.1
Evtl.:
Wdh. Bruchrechnung
Aufgaben:
S 69 Nr.2a-d
Aufgaben:
S 70 Nr.3a-e
2⋅2⋅2⋅2 2 2 2 2 2 4
=
=( )
3⋅3⋅3⋅3 3 3 3 3 3
HAufgaben: S 69 Nr.2e-l
Aufgaben:
S 70 Nr.5 Wichtig: Beispiel an Tafel
Aufgabe:
S 70 N.7
3.5 Potenzen mit rationalem Exponenten
Einleitung:
Aus Buch.
„Die griechische Insel Delos wird von einer Seuche heimgesucht. Das Orakel
rät den Altar (1,2mx1,2m1,2m) in Doppelter Größe zu bauen.
a)Was bedeutet „in doppelter Größe?“ 1,73m³ → 3,46m³
b)Welche Kantenlänge hat der neue Altar? Schätze gut ab
x³=3,46
| Gesucht ist die „Gegenrechnung zu Hoch3“
x³=3,46
|3√ sprich:dritte Wurzel (GTR:Math: 3x√3,46
x=3√3,46=1,51
Merke:
•
Die n-te Wurzel ist die Gegenrechnung zu „Hoch n“ n√(3,2)n=3,2
•
Man schreibt statt n√a=a1/n
•
a1/n muss nämlich auch die Gegenrechnung zu „Hoch n“ sein. Beweis:
•
Beweis (a n ) n =an⋅ n =a 1=a
1
1
Vergleiche: a +n−n=a und a⋅n: n=a
Beispiele:
1
•
√3 1000=1000 3 =10 „Hoch drei rückgängig machen
•
4
√8 9 =(9 8 ) 4=9 8 =9 2 =3 „Hoch zwei rückgängig machen
1
4
1
Aufgaben:
S 72 Nr. 1
Aufgaben:
Je ein Beispiel an Tafel, dann eigenständiges Üben
S 72 Nr. 2 b-d) 3 b-d) 4b-d) 9b-d)
S 72 Nr. 12
3.6 Potenzgleichungen
Einstieg:
Folie → Merke-kasten übertragen.
Aufgaben:
S 76 Nr. 1 a-d
Forme die Gleichung zunächt zu einer einfachen Potzenzgleichung um
a)
12x11=84
x≈1,19
b)
2x³+3=4x³+11
x≈1,59
c)
(x +3)(x -3)=10
x=1 und x=-1
Wdh:
4
4
Betimme mit dem GTR: Für welche x-Werte Treffen sich die Funktionen:
a)f(x)=2x+1 und f(x)=-x+3
b)f(x)=x4-1 und f(x)=-x6+1
Löse mit dem GTR:
x3=x4-1
S76 Nr. 3 a-f)
HA:
S 76 Nr.1e-h Nr. 2 a-c
Wdh:
Wir bestimmen mit dem GRT die Lösung des LGS
Aufgabe:
S 76 Nr. 4 und 5
Wdh:
Stationenlernen
3.7 Der Logartihmus
Märchenzahlen: 3,7,12,1000
In einem Land gab es 3 Hexen, jede hatte (je) 3 Katzen. Die zogen an (je) 3 Tagen aus
und fraßen (je) 3 fette Ratten.
a)Schreibe als Potenzgleichung wie viele Ratten gefressen werden,
b)Wie viele 3er Stationen braucht die Geschichte für 1000 Ratten. (1 Dezimale machbar)
c)Schreibe b als Gleichung mit x. → 3x=1000
Potenzgleichung (Suche Basis)
Exponentialgleichung (Suche Exponent)
x7
x
x
3x
x
x
=1000
|7√
=7√1000
=10001/7≈2,68
=1000
|log3
=3log(1000) „3er Logarithmus von 1000“
≈6,29
Lesen:
S 77 Beispiele
Tafel:
3
log(81)=____
denn 3__=81
2
log(1/8)=____
denn 2___=1/8 → x=-3
→ x= 4
Aufgabe:
S 78 Nr. 1 a-c 2 a-c 3 a-c) für Schnelle: Schreibe Nr2 a-c als Potenzgl
Haufgabe:
S 78 Nr. 1,2,3 je fertig
Aufgaben:
S 78 Nr. 6,7,5 je a und b
3.8 Exponentialgleichungen
Merke:
Für jeden Logarithmus gilt:
Wir wissen schon:
log (ab )=b⋅log (a )
a x =b dann x =log a (b) =________
Der GTR hat aber nur den log10=log → LOG-Knopf
3x
=1000
|log10
log(3x)=log(1000)
x log(3)=log(1000) | /log(3)
x
=log(1000)/log(3)
x
≈6,29
Aufgabe:
S 79 Nr. 2 a-g
Haufgabe:
S 79 Nr. 1
Aufgabe:
Youtube: „Gangnam Style“: 1.Tag: 5 2.Tag 25 3. Tag: 125 ….
a)Wie lange dauert es bis das Video 800 Mio. Klicks hat? Löse mit Log
b)Durch welche Basis (statt 5) muss man wählen, damit es nach einem
Monat 10Mio Klicks hat?
Aufgabe:
S 79 Nr. 3ab S 80 Nr. 4 ab Nr. 5ab Für schnelle: 7ab
S 80 Nr. 8
Potenz vs. Logarithmus
Drei wichtige Gesetze hängen zusammen.
Potenz
a x+ y =a x⋅a y
a x− y =a x :a y
y
( a x ) =a x⋅y
Logarithmus
log a (x⋅y)=log a ( x)+log a ( y )
...
log a ( x y )= y⋅log a x
Beispiel
log 2 ( 4 ·8)=log 2 (4)+log 2 (8)=2+3=5
log 2 (32 : 4)=...
Aufgabe 1:
Fülle die Lücken.
Aufgabe 2:
Wende eines der Logarithmen-Gesetze an
a)
log( a)+log(b)
b)
log( a²)−log(b)
c)
log( a²)−log(
d)
log( x +1)+ log(2x +3)
e)
1
⋅log(a x−1)
2
(x−1)
Gaufgabe:
1
)
a3
S81-82 Zwei Aufgaben aus Nr.1-12 und eine aus Nr. 13-18
Eine der Aufgaben müssen auf Folie präsentiert werden.
Bingo:
x² −10x+ 25=0
2
x
2 ⋅2 =2
sin( x)+sin( x)=0,517
3⋅2 +2⋅2 =4⋅2 +64
Zahl n bei der die
Summe der Teiler=2n
15 6 7 8 6 3 4
9x +3x =2 x + 2430
(2x−6)
x
5
x
5
x
5
2
2
24 + x =25
2
x 2−( x 2 + x )=2x−12
3.9 Wdh. Lineare Gleichungen
Aufgabe:
Gerade y=m·x+c z.B. y=2x+3
•
Zeichne mit c=3 und m=-1,5 c=1,5 und m=3/7
•
Bestimme mit/ohne Zeichnung m und c, wenn die Gerade die Punkte
A(1|3) und B(2|5) A(3|8) und B(1|5) enthält
•
Mit/Ohne Zeichnung: Gib ein Lineares Gleichungssystem an, welches
x=3 als Lösung hat.
Arbeitsblatt: Subtraktionsverfahren/Gleichsetzungsverfahren