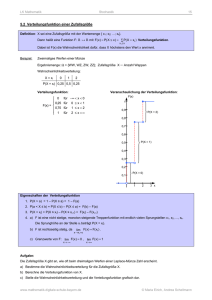
Zufallsgröße

107 Wegener BM/4/ZuVar/q Freitag 23.05.2003 12:37:34
Wahrscheinlichkeit
Zufallsgröße
Eine auf einer (Ereignis-)Grundmenge S definierte reellwertige Funktion X
heißt Zufallsgröße (zufällige Größe, Zufallsvariable), wenn jedem Intervall
[-∞,x] von X eine (Ereignis-)Teilmenge von S entspricht.
Je nach Mächtigkeit der Grundmenge und Ausschöpfung des Wertebereiches
heißt X diskret oder stetig.
Die Wahrscheinlichkeit, dass die diskrete Zufallsgröße X die Realisierung x
hat, wird mit P(X=x) bezeichnet.
Bei stetigen Zufallsvariablen lässt sich keinem einzelnen Wert, sondern nur
einem Intervall eine Wahrscheinlichkeit zuordnen! (Also: P(X=x)=0 für jede reelle Zahl x bei jeder stetigen Zufallsvariable! Aber: P(a<X≤b) kann bei a<b
verschieden von Null sein.)
 Dr. Gerd Wegener, Hannover 2003
1
Wahrscheinlichkeit
Verteilungsfunktion
Die Verteilungsfunktion F(x) einer Zufallsgröße X ist definiert als
F(x)=P(X≤x). Es ergibt sich damit aus der Definition der Wahrscheinlichkeit,
dass für jede Verteilungsfunktion F gilt F(-∞)=0 und F(+∞)=1.
Die erste Ableitung einer stetigen Verteilungsfunktion f(x)=F’(x) heißt Verteilungsdichte oder Wahrscheinlichkeitsdichte. Die Fläche unterhalb einer
Dichtefunktion ist stets gleich eins. Wahrscheinlichkeiten von Zufallsgrößenintervallen werden durch die Fläche der Dichte repräsentiert.
 Dr. Gerd Wegener, Hannover 2003
2
Wahrscheinlichkeit
Zufallsgrößen
Beispiele
S={
,
,
,
,
,
}
Zufallsgröße "Augenzahl"
→1
→2
→3
→4
→5
→6
p(X=x): p(X=1) = p(X=2) = p(X=3) = p(X=4) = p(X=5) = p(X=6) =
Zufallsgröße "Sechs"
→0
p(X=x): p(X=0) =
 Dr. Gerd Wegener, Hannover 2003
→0
5
6
→0
p(X=1) =
1
6
→0
→0
→1
1
6
3
Wahrscheinlichkeit
Zufallsgröße und Verteilungsfunktion
1
2/3
1/3
F(x)
2/3
1/3
p(X=x)
1
Beispiel
0
1
2
3
4
"Augenzahl"
 Dr. Gerd Wegener, Hannover 2003
5
6
7
0
1
2
3
4
"Augenzahl"
5
6
7
4
Wahrscheinlichkeit
Zufallsgröße und Verteilungsfunktion
1
2/3
1/3
F(x)
2/3
1/3
p(X=x)
1
Beispiel
-1
0
1
"Sechs"
 Dr. Gerd Wegener, Hannover 2003
2
-1
0
1
"Sechs"
2
5
Wahrscheinlichkeit
Zufallsgröße
Erwartungswert
Der Erwartungswert E(X) einer Zufallsgröße X ist definiert als
K
K
µ = E(X) = ∑xi·P(X=xi) = ∑xi·pi
i=1
+∞
für diskrete und
i=1
µ = E(X) = ∫u·f(u)du
für stetige Zufallsgrößen.
-∞
Beispiele
6
6
µ = E("Augenzahl") = ∑xi·pi = ∑i· = + + + + + =
i=1
6
i=1
1
1
2
3
4
5
6
21
6
6
6
6
6
6
6
6
µ = E("Sechs") = ∑xi·pi = + + + + + =
i=1
 Dr. Gerd Wegener, Hannover 2003
0
0
0
0
0
1
1
6
6
6
6
6
6
6
= 3,5
6
Wahrscheinlichkeit
Zufallsgröße
Varianz
Die Varianz V(X) einer Zufallsgröße X ist definiert als
K
σ = V(X) = E((X-µ) ) = ∑(xi-µ)2·pi = E(X2)-(E(X))2
2
2
für diskrete und
i=1
+∞
σ2 = V(X) = E((X-µ)2) = ∫(u-µ)2·f(u)du = E(X2)-(E(X))2
für stetige
-∞
Zufallsgrößen.
Beispiele
6
σ = V("Augenzahl") = ∑(xi 2
i=1
=
225
216
+
81
216
+
9
216
+
6
9
216
+
21 2
) ·pi
6
81
216
+
σ = V("Sechs") = ∑(xi - )2·pi =
2
i=1
 Dr. Gerd Wegener, Hannover 2003
225
216
1
1
6
216
6
= ∑(i i=1
=
+
630
216
1
216
21 2 1
)·
6
6
= 2,917
+
1
216
+
1
216
+
1
216
+
25
216
=
30
216
= 0,139
7