Übungsblatt 4

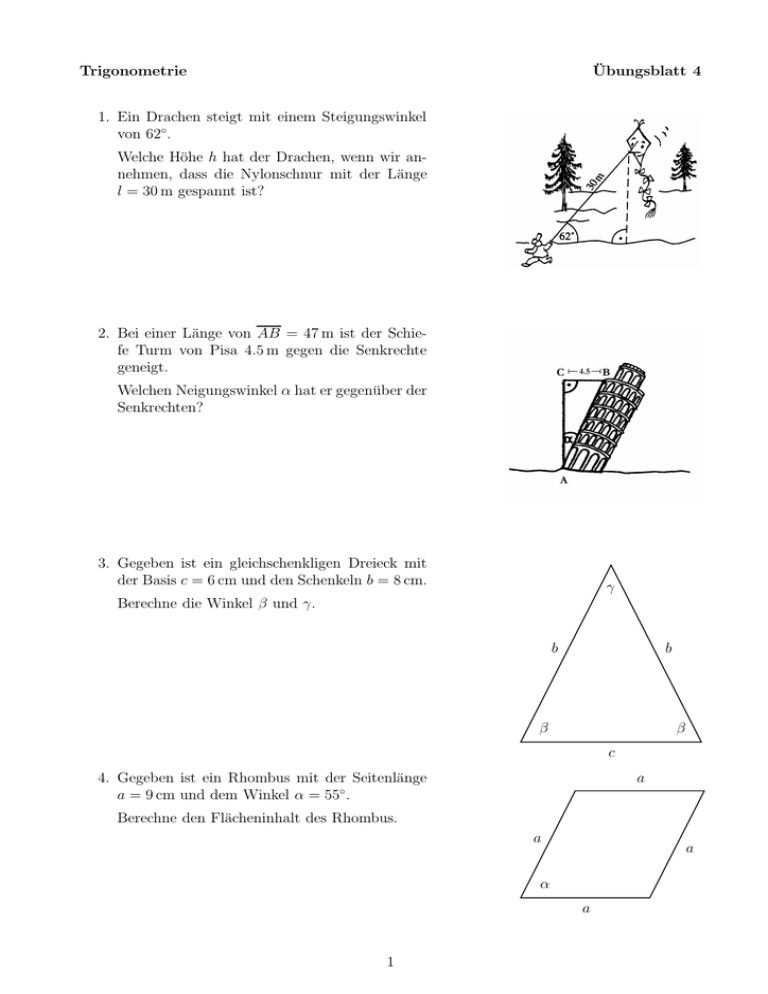
Trigonometrie
Übungsblatt 4
1. Ein Drachen steigt mit einem Steigungswinkel
von 62◦ .
Welche Höhe h hat der Drachen, wenn wir annehmen, dass die Nylonschnur mit der Länge
l = 30 m gespannt ist?
2. Bei einer Länge von AB = 47 m ist der Schiefe Turm von Pisa 4.5 m gegen die Senkrechte
geneigt.
Welchen Neigungswinkel α hat er gegenüber der
Senkrechten?
3. Gegeben ist ein gleichschenkligen Dreieck mit
der Basis c = 6 cm und den Schenkeln b = 8 cm.
γ
Berechne die Winkel β und γ.
b
b
β
β
c
a
4. Gegeben ist ein Rhombus mit der Seitenlänge
a = 9 cm und dem Winkel α = 55◦ .
Berechne den Flächeninhalt des Rhombus.
a
a
α
a
1
5. Die Cheopspyramide in Ägypten hat eine quadratische Grundfläche mit der Seitenlänge a = 230 m
und die Höhe h = 137 m.
S
Berechne den Winkel α zwischen der Diagonalen
AC und der Seitenkante AS.
D
α
C
a
F
A
B
a
6. Gegeben ist ein gleichschenkligen Dreieck mit
dem Winkel γ = 46◦ und der Basis c = 6.4 cm.
γ
Berechne die Länge b der beiden Schenkel.
b
b
β
β
c
7. Berechne die Grössen der Winkel α, β und γ eines allgemeinen Dreiecks mit den Seitenlängen
a = 13 cm, b = 4 cm und c = 15 cm.
Hinweis: Bestimme zuerst den Flächeninhalt
des Dreiecks mit Hilfe des Satzes von Heron und
damit die Höhe hc .
γ
a
b
β
α
c
2
Trigonometrie
1.
Lösungen
h
= sin 62◦
l
h = l · sin 62◦
h = 30 m · sin 62◦
h = 26.49 m
2. sin α =
BC
AB
BC
AB
4.5 m
α = arcsin
47 m
α = arcsin
α = 5.49◦
3. cos β =
c/2
b
c
2b
6 cm
β = arccos
16 cm
β = arccos
β = 67.98◦
γ = 180◦ − 2β
γ = 44.04◦
4. sin α =
ha
a
ha = a · sin α
A = a · ha = a · a · sin α = a2 sin α
A = (8 cm)2 · sin 55◦
A = 52.43 cm2
5.
• AF =
√
1
1
· AC = · a · 2
2
2
AF = 162.64 m
• tan α =
h
AF
h
AF
137 m
α = arctan
162.64 m
α = arctan
α = 40.11◦
1
Übungsblatt 4
6.
sin(γ/2) =
c/2
b
b · sin(γ/2) = c/2
b=
c/2
sin(γ/2)
b=
3.2 cm
sin 23◦
b = 8.19 cm
7. a = 13 cm, b = 4 cm, c = 15 cm
s = (a + b + c)/2 = 16 cm
p
A = s(s − a)(s − b)(s − c) = 24.0 cm
A=
c · hc
2
sin α =
⇔
hc =
2·A
= 3.2 cm
c
⇒
γ = 112.62◦
hc
b
α = arcsin
hc
b
α = 53.13◦
sin β =
hc
a
β = arcsin
hc
a
β = 14.25◦
γ = 180◦ − α − β
2