Uebung 2 - htw saar

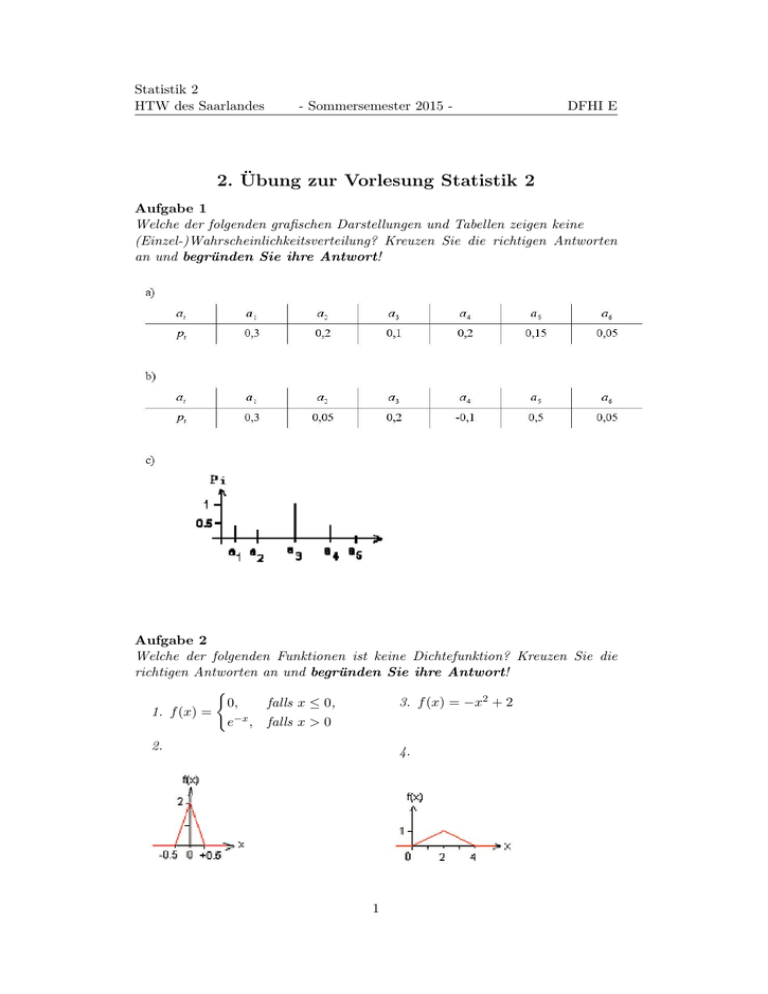
Statistik 2
HTW des Saarlandes
- Sommersemester 2015 -
DFHI E
2. Übung zur Vorlesung Statistik 2
Aufgabe 1
Welche der folgenden grafischen Darstellungen und Tabellen zeigen keine
(Einzel-)Wahrscheinlichkeitsverteilung? Kreuzen Sie die richtigen Antworten
an und begründen Sie ihre Antwort!
Aufgabe 2
Welche der folgenden Funktionen ist keine Dichtefunktion? Kreuzen Sie die
richtigen Antworten an und begründen Sie ihre Antwort!
(
3. f (x) = −x2 + 2
0,
falls x ≤ 0,
1. f (x) =
e−x , falls x > 0
2.
4.
1
Statistik 2
HTW des Saarlandes
- Sommersemester 2015 -
DFHI E
Aufgabe 3
Welche der folgenden Funktionen ist keine Verteilungsfunktion? Kreuzen Sie
die richtigen Antworten an und begründen Sie ihre Antwort!
(
4. F (x) = 1 − e−|x|
0,
falls x ≤ 0,
1. F (x) =
(1 + e−x ), falls x > 0
5.
(
0,
falls x < 0,
2. F (x) =
−x
(1 − e ), falls x ≥ 0
3.
Aufgabe 4
In einem Lieferung von 10 Motorteilen befinden sich 3 defekte Teile.
Zur Qualitätskontrolle werden nacheinander 4 Teile gezogen, ohne sie nach der
Ziehung wieder ins die Lieferung zurück zu legen.
Sei X die Anzahl der unter diesen 4 gezogenenen Teilen vorhandenen defekten
Teile.
1. Berechnen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße X, d.h.
po = P (X = 0), p1 = P (X = 1), p2 = P (X = 2) und p3 = P (X = 3).
2. Berechnen Sie den Erwartungswert E(X), die Varianz V ar(X) und das
obere Quartil x0.75 .
Aufgabe 5
Die zufällige Zeit X, die ein ICE in Saarbrücken verspätet eintrifft, liegt zwischen 0 und 100 Minuten. Die Dichtefunktion ist in folgender Skizze gegeben.
2
Statistik 2
HTW des Saarlandes
- Sommersemester 2015 -
DFHI E
Berechnen Sie
1. die Dichtefunktion von X.
2. die Verteilungsfunktion von X.
3. den Anteil der Fällen, in denen die Verspätung eine halbe Stunde überschreitet. Stellen Sie diesen Anteil grafisch dar!
4. die Wahrscheinlichkeit dafür, dass der ICE sich mehr als 1 Stunde verspätet, wenn man bereits eine halbe Stunde (Verspätung) auf den ICE
gewartet hat.
5. Welche Verspätungszeit wird in 70% aller Fälle überschritten?
6. Wie groß ist die Verspätung im Mittel?
Aufgabe 6
Die zufällige Lebensdauer X eines Handyakkus (in Jahren) hat folgende Dichtefunktion:

 −6 x2 + 6 x , 0 ≤ x ≤ 5
fX (x) = 125
25
0
, sonst
a) Zeigen Sie, dass fX (x) eine Dichtefunktion ist.
b) Berechnen Sie die Verteilungsfunktion FX (x) von X.
c) Wie groß ist die durchschnittliche Lebensdauer der Handyakkus?
d) Wieviel Prozent der Akkus leben länger als 2 Jahre?
e) Berechnen Sie den Anteil der Handyakkus, die länger als 3 Jahre leben,
wenn sie bereits 2 Jahre überlebt haben.
Aufgabe 7
Gegeben ist eine stetige Zufallsvariable mit folgender Verteilungsfunktion:
(
0
,x ≤ 1
f (x) =
−2
1−x
, sonst
1. Berechnen Sie die Dichtefunktion.
2. Berechnen Sie den Erwartungswert.
3. Berechnen Sie P (1, 5 ≤ x ≤ 2, 25).
4. Berechnen Sie P (x ≤ 3, 5|x ≤ 1, 5).
5. Berechnen Sie das 0,25-Quantil.
3
Statistik 2
HTW des Saarlandes
- Sommersemester 2015 -
DFHI E
Aufgabe 8
Die Anzahl der zerfallenen Atomkerne bei radioktiven Zerfall ist poissonverteilt. Im Mittel zerfallen bei einem bestimmten Präparat 150 Atomkerne pro
Minute.
1. Wie groß ist die Wahrscheinlichkeit dafür, dass höchstens 3 Kerne pro
Sekunde zerfallen?
2. Wie groß ist die Zeit zwischen dem Zerfall von 2 Atomkernen im Durchschnitt?
3. Wie groß ist die Wahrscheinlichkeit dafür, dass die Zeit zwischen dem
Zerfall von 2 Kernen mindestens 5 Sekunden beträgt?
Aufgabe 9
Die Zeit, die ein elektronisches Bauteil ohne Störung läuft, ist exponentialverteilt mit dem Parameter α = 0.03.
1. Wieviel % aller Bauteile arbeiten mehr als 40 Tage störungsfre?
2. Welche störungsfreie Zeit überschreiten 80% aller Bauteile nicht?
3. Wie lange arbeiten die Bauteile im Durchschnitt störungsfrei?
Aufgabe 10
Bei der Übertragung von elektronischen Signalen wird ein Signal mit einer
Wahrscheinlichkeit von p = 0.1 fehlerhaft übertragen. Eine Nachricht besteht
aus 8 Signalen. Berechnen Sie die Wahrscheinlichkeit dafür, dass:
a) genau das 2. Signal fehlerhaft übertragen wird.
b) genau eines der Signale fehlerhaft übertragen wird.
c) genau das zweite und das fünfte Signal fehlerhaft übertragen wird.
d) genau zwei Signale fehlerhaft übertragen werden.
e) höchstens ein Signal fehlerhaft übertragen wird.
Aufgabe 11
Die durchschnittliche Niederschlagsmenge (Regenmenge) pro Monat in Deutschland ist normalverteilt um 58 Liter pro Quadratmeter: X ∼ N (58, (20)2 ).
1. Wie groß ist die Wahrscheinlichkeit, dass es in einem Moment mehr als
70 Liter pro Quadratmeter regnet?
2. Berechnen Sie den Toleranzbereich ( [58 − , 58 + ]) um 58 mm herum,
d.h. das , in dem in 99% aller Fälle die Niederschlagsmenge im Monat
liegen.
4
Statistik 2
HTW des Saarlandes
- Sommersemester 2015 -
DFHI E
Aufgabe 12
Die zufällige Übertragungszeit T von Bildsignalen durch einen Kanal K sei normalverteilt mit dem Erwartungswert µ = 50 ms und der Varianz σ 2 = 4ms2 ,
d.h. es gelte T ∼ N (50, 4).
Signal
K
Empfänger
a) Wie groß ist die Wahrscheinlichkeit dafür, dass die Übertragungszeit genau 42 ms dauert?
b) Mit welcher Wahrscheinlichkeit liegt die Übertragungszeit zwischen 42 und
53 ms?
c) Geben Sie einen symmetrischen Bereich [50 − c, 50 + c] ms um die mittlere
Übertragungszeit an, in dem 90 % aller Zeiten liegen!
d) Mit welcher Wahrscheinlichkeit beträgt die Übertragungszeit eines Bildsignales mehr als 50ms?
e) Wie groß ist die Wahrscheinlichkeit dafür, dass bei 5 (stochastisch unabhängigen) Übertragungen bei mindestens einer die Übertragungszeit mehr
als 50 ms beträgt?
f ) Wie viele Übertragungen, die länger als 50ms dauern, würden Sie durchschnittlich bei 100 stochastisch unabhängigen Übertragungen erwarten?
g) Angenommen, Sie schalten 2 dieser Kanäle in Reihe. Mit welcher Wahrscheinlichkeit überschreitet die Gesamt-Übertragungszeit dann 100 ms?
Signal
K1
K2
Empfänger
Aufgabe 13
Eine Gerät besteht aus 3 Bauelementen, wie in der Skizze dargestellt. Das Gerät
fällt aus, wenn beide Reihen ausfallen. Eine Reihe fällt aus, wenn mindestens
eines der in Reihe geschalteten Elemente ausfällt.
Die zufällige Zeit Ti bis zum Ausfall eines Bauelements Bi ist wie folgt gegeben
(alle Angaben in Stunden):
• Bauelement B1 : T1 ∼ N (100, 1)
• Bauelement B2 : Die Verteilung von T2 ist nicht vollständig bekannt.
• Bauelement B3 : T3 ∼ E(0, 01)
B1 fällt unabhängig von B3 aus, gleichfalls fällt B2 unabhängig von B3 aus (d.h.
T1 und T2 sind stochastisch unabhängig von T3 ). Die Ausfallwahrscheinlichkeit
von B2 ist von der Lebensdauer von B1 abhängig; es gilt:
P (T2 < 100/T1 < 100) = 0, 99 und P (T2 < 100/T1 ≥ 100) = 0, 2.
5
Statistik 2
HTW des Saarlandes
- Sommersemester 2015 -
DFHI E
Berechnen Sie die Wahrscheinlichkeit dafür, dass die Lebensdauer des Gerätes
100 Stunden nicht überschreitet !
Abgabe: Freitag, 31. Juli 2015 vor der Vorlesung
6