Technische Mathematik (8)

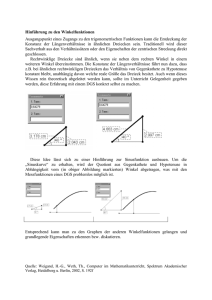
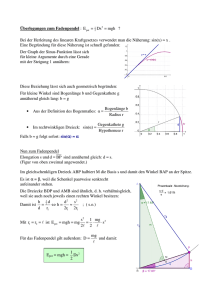
GELERNT IST GELERNT
Technische Mathematik (8)
GRUNDLAGEN In der vorangegangenen Folge bildete die Berechnung des rechtwinkligen
Dreiecks mittels Satz des Pythagoras den Schwerpunkt. Der Autor Karl-Heinz Bleiß stellt in
diesem Beitrag die Winkelfunktionen vor und geht in Beispielen näher darauf ein.
Z
eichnet man zu einer Seite eines rechtwinkligen Dreiecks parallele Seiten und verändert die beiden anderen Seitenlängen entsprechend, dann entstehen weitere Dreiecke mit gleichen Winkeln –
so genannte mathematisch ähnliche Dreiecke (Bild 14). Diese haben neben gleichen Winkeln auch gleiche Seitenverhältnisse. Mit
α1 = α2 = α3 und β1 = β2 = β3 sind:
Cosinus
Tangens
b1 b2 b3
=
=
= ...
c1 c2 c3
c1 c2 c3
= = = ...
b1 b2 b 3
Cotangens
b1 b2 b3
=
=
= ...
a1 a2 a3
c1 c2 c3
= = = ...
a1 a2 a3
c)
β
se
nu
ote
p
Hy
α
α
Ankathete
β
c
a
α
Gegenkathete
b
b2
b3
Bild 14: Mathematisch
ähnliche Dreiecke
74
Bild 15a und b: Seitenbezeichnungen in Bezug zu einem
betrachteten Winkel: 15a Bezugswinkel α
15b Bezugswinkel β
Quelle: K.-H. Bleiß
b1
Auf dem Taschenrechner wird die Taste für die Umkehrfunktion allerdings meistens nicht mit »arc…« sondern mit der jeweiligen Winkelfunktion und dem Exponenten »–1« bezeichnet, also beispielsweise
Ankathete
e
us
ten
po
y
H
a2
a1
α1
Gegenkathete
Ankathete
Ankathete
Gegenkathete
sin 30° = 0, 5
α = arc sin 0, 5 = 30°
Gegenkathete
β1
bezogen auf α
Gegenkathete
Hypotenuse
Ankathete
Hypotenuse
b)
a3
allgemein
man auf den Cotangens verzichten, weil durch richtiges Umstellen
der Bestimmungsgleichung mit einer der drei ersten Winkelfunktionen jede Seite berechenbar ist. Sobald eine Seite und ein Winkel
(zusätzlich zu dem rechten) bekannt sind, lassen sich alle fehlenden
Seiten bestimmen. Umgekehrt lässt sich aus einem Seitenverhältnis
(Winkelfunktionswert) mit der Umkehrfunktion der Winkel bestimmen. Unter Umkehrfunktion ist hier mathematisch, das Aufsuchen
eines dazugehörenden Winkels bei bekanntem Winkelfunktionswert
gemeint. Man nennt diese Umkehrung »Arcus-Funktion«:
arc sinα = α
Hier ein kleines Beispiel zur Veranschaulichung:
β
β2
bezogen auf
einen Winkel für
Tabelle 2: Namen und Seitenverhältnisse der Winkelfunktionen
a)
β3
Quelle: K.-H. Bleiß
Sinus
a1 a2 a3
= = = ...
b1 b2 b 3
Es gibt in jedem Dreieck sechs mögliche Seitenverhältnisse. Davon
sind im rechtwinkligen Dreieck vier mit Namen versehen. Die Seitenverhältnisse sind nur eindeutig, wenn man die beiden Katheten unterscheidet. Für eine eindeutige Zuordnung dienen die Winkel und man
spricht von Ankathete und Gegenkathete. Die Kathete, die an dem
betrachteten Winkel liegt, heißt »Ankathete«. Die zweite Kathete, liegt
dem betrachteten Winkel gegenüber und heißt dementsprechend
»Gegenkathete« (Bild 15a und b). Die Namen der Winkelfunktionen
(Seitenverhältnisse) sind in Tabelle 2 zusammengestellt (Bild 15c).
Wichtig zu erwähnen ist noch, dass die Bezeichnungen »An- und Gegenkathete« nur in Zusammenhang mit einem Winkel verwendet werden dürfen.
Den Cotangens wird man auf dem Taschenrechner vergeblich
suchen, denn er ist der Kehrwert des Tangens und ist somit aus dem
Tangens mit Hilfe der Kehrwerttaste zu berechnen. Generell kann
α2
Winkelfunktion
a1 a2 a3
=
=
= ...
c1 c2 c3
Winkelfunktionen
α3
SEITENVERHÄLTNISSE DER WINKELFUNKTIONEN
Bild 15c: Allg. Seitenbezeichnungen des Dreiecks in Zusammenhang mit der Betrachtung
der Winkelfunktionen (s. Tab. 2)
de 8.2015
GELERNT IST GELERNT
AUFGABE »SCHLÜSSELWEITE« – DREI LÖSUNGSWEGE
Lösung 2
sw # d2 "
( d)
sw # d2 " & '
$2%
2
d
4
sw # 602 mm2 "
sw = 51,96mm
602 mm2
4
sw
2
60 °
d
2
2
( 60mm )
sw # 602 mm2 " &
'
$ 2 %
sw = 51,96mm
sw = 52mm
60 °
α = 60 °
2
d
α = 60 °
d
2
sw = 52mm
Tabelle 3: Die drei Lösungswege resultieren aus den Ansätzen über den Pythagoras
und der Winkelfunktion »sin«
»sin–1«. Diese Zuordnung muss man schon kennen, sonst läge die
Vermutung nahe, sin–1 von 0,5 wäre der Kehrwert von 0,5 – also der
Wert »2«. Gemeint ist hier aber: sin–1 von 0,5 entspricht dem Winkel
von »30 °«.
In geschriebener Form wird die Schreibweise mit »arc…« bevorzugt. In technischen Abhandlungen findet man allerdings auch oft
eine verkürzte Schreibweise mit einem Pfeil, der die Bedeutung
»daraus wird:« beinhaltet:
sin 30° = 0, 5
arc sin 0, 5 = 30 °
sin α 0, 5 α = 30 °
Nicht zulässig ist im Übrigen diese Schreibweise:
Darstellungsweise eines Taschenrechners
Am Beispiel des einfachen Windows-Rechners (Windows 7), den
man über die Zubehörprogramme erreicht, möchte ich die Bearbeitung einer einfachen Umkehrung beschreiben. Ist die »Inv-Taste«
gedrückt, erscheinen die Tasten »sin«, »cos« und »tan« als »sin–1«,
»cos–1« und »tan–1« (Bild 16a).
Das zugehörige Zahlenbeispiel ist ebenfalls im Bild enthalten
(s. Display). Aus den Seitenlängen des Dreiecks ergibt sich für den
Tangens der Wert »1,75«. Gibt man diesen Wert in den Rechner ein
(bei aktiver »Inv-Taste«) und drückt »tan–1«, so erhält man den Wert
»60,2551187…« (Bild 16b), das entspricht einem Winkel von 60,26 °.
Bild 17: Wiederholung der Aufgabe »Schlüsselweite« aus Heft 06.2015 – dreierlei Lösungsmöglichkeiten
Zum direkten Vergleich sind die verschiedenen Lösungswege in einer
Tabelle zusammengefasst (Tabelle 3). Das Thema ermöglicht natürlich noch eine Vielzahl weiterer Beispiele und Betrachtungen und ist
speziell für Berechnungen in der Wechselstromtechnik ein wichtiges
Werkzeug.
In der Wechselstromtechnik wird z. B. von sinusförmiger Spannung
gesprochen. Die meisten Elektrofachleute werden damit einen Spannungsverlauf verbinden, der eine wechselnde Polarität besitzt und
eine charakteristische Form hat. Das Entstehen dieser Form ist allerdings mathematisch begründet. Alle Winkelfunktionen lassen sich in
einem Liniendiagramm als Verlaufskurve über den Winkeln darstellen. Üblicherweise geht man bei der Erklärung vom so genannten
Einheitskreis aus. Der Einheitskreis ist ein Kreis mit dem einheitslosen
Radius »1«. Die Verlaufskurven werden normalerweise über 360 ° abgebildet. Das bedeutet in der Wechselstromtechnik, den Kurvenverlauf über eine Periode.
Einstellungen am Taschenrechner
Vor diesen Betrachtungen sollte man berücksichtigen, dass es drei Möglichkeiten gibt, den Winkel anzugeben. Der Normalfall ist, das Messen in
»Grad« (°) damit sind »Altgrad« (englisch: degree) gemeint. Der rechte
Winkel hat hierbei 90° und der Vollwinkel 360°. Beim Bestreben auch
die Winkel besser in das Dezimalsystem zu integrieren, hat man entsprechend »Neugrad« mit einem rechten Winkel von 100 Grad definiert.
a)
b)
β
Beispielaufgabe »Schlüsselweite«
Diese Aufgabe war schon am Ende des vorangegangenen Beitrags in
»de« 06.2015 Thema. Mit dem Wissen der beiden Beiträge (»Satz
des Pythagoras« und »Winkelfunktionen«), können wir nun die Rechnung auf drei Arten ausführen. Nochmals die Aufgabenstellung: Wie
groß ist die maximale Schlüsselweite (sw) eines regelmäßigen Sechsecks, die an einen Rundstahl mit einem Durchmesser von d = 60 mm
gefräst werden kann?
• Gegeben sind: Anzahl der Ecken n = 6, der Durchmesser d = 60 mm
• Gesucht ist: Schlüsselweite sw = ?
www.elektro.net
sw
sw
Quelle: K.-H. Bleiß
( d)
sw 2 # d2 " & '
$2%
sw 2 d2 d2
#
"
!4
4
4 16
( d2 d2 )
sw 2 # 4 ! & " '
$ 4 16 %
Lösung 3
2
c
α
b = 4 cm
tan α = 7 cm = 1,75
4 cm
a =7 cm
Quelle: K.-H. Bleiß
Lösung 1
d
4
Bild 16a und b: Beispielaufgabe mittels Taschenrechner
75
gelernt ist gelernt
Dieses Winkelsystem hat sich, zumindest in der Elektrotechnik,
nicht durchgesetzt. Die dritte Möglichkeit ist die Bogenlänge im Einheitskreis (Bogenmaß). Diese Angabe beruht darauf, dass man jedem
Winkel des Einheitskreises ein zugehöriges Stück seines Umfangs
zuordnet. Die Zuordnung, die daraus entsteht ist, dass 360 ° im Altgradsystem dem vollen Umfang des Einheitskreises 2 π entsprechen.
Jede dieser Winkelangaben ermöglicht mit Hilfe eines Taschenrechners das Berechnen der Winkelfunktionen. Wichtig ist dabei,
dass der Rechner (Bild 16a) richtig eingestellt wird: Für Altgrad »Deg«
– Taste über der sin-1-Taste – (Einheit: Grad, Kurzzeichen: °), »Grad«
76
für Neugrad (Einheit: Gon, Kurzzeichen: g) und »Rad« für Radiant
(Bogenmaß), der einheitenlos ist. Eine Fortsetzung dieses Themas ist
der Schwerpunkt der nächsten Folge.
(Fortsetzung folgt)
Autor
Karl-Heinz Bleiß
Fachautor Hatten
de 8.2015