- Klett und Balmer Verlag

standen sein kann. Begründe deine Entscheidung. Gib gegebenenfalls den Streckfaktor an und zeichne das Streckzentrum ein.
a)
b)
c)
Korrigendum Lambacher Schweizer 9/10, 1. Auflage 2011
Klett und Balmer Verlag, Baar. April 2014.
Seite 26, Aufgabe 4
d) Zeichne selbst Figuren wie in a) bis c) und lass sie von deinem Nachbar untersuchen.
4 a)
Tipp:
Suche dir Punkte auf
dem Kreis, die du zur
Bestimmung heranziehen kannst
Bestimme das Streckzentrum und den Streckfaktor der zentrischen Streckung.
b)
c)
Lösung:
u
u
a) cos (a) = _
r + s
 
= _
ur  , tan (c) = _ t   = _ hs  
s_
b) t   = cos (c) (Dreieck DBC), u
_ hr   = tan (a) (Dreieck ABD), Die Figuren werden durch eine zent­
_ ht   = sin (c) (Dreieck DBC), rische Streckung mit dem angegebenen 5
Seite 35, Aufgabe 14Streckfaktor k auf eine Bildfigur abge­
_
r + s
 
= cos (a) = sin (c) bildet. Bestimme die Flächeninhalte von Aufgaben
B
26 1 cm
A
Original­ und Bildfigur.
14
Der Sekanten­ und der Sekanten­Tan­
genten­Satz 1 Bestimme für das rechtwinklige Dreieck in Fig. 1 mithilfe des Taschenrechners die c
a
C
(Dreieck ABC) t
_
a)
 
= sin (a) = cos (c) b) (Dreieck ABC)
r + s
k=3
k = 0.5
t_
u   = tan (a) (Dreieck ABC)
b
A
Fig. 1
a) Beweise den Sekantensatz: Schneiden Grösse der Winkel a und b. B
t
Sekanten durch S einen Kreis (Fig. 1), dann a) a = 3 cm; c = 8 cm b) b = 5 cm; c = 10 cm c) a = 15 cm; b = 12 cm
9
Welche der Angaben zu Fig. 1 gehören zusammen? Ordne zu und schreibe mit Gleich­
sind die Produkte der Streckenlängen von M
S
a b
a
heitszeichen.
S zu den jeweiligen Kreispunkten konstant: _
2 Bestimme für das Dreieck in Fig. 1 den Wert der Seitenverhältnisse c   , _ c   und _ b . 
__
__
__ __
D
SB SA  = SD   · SC   Cc) a = 25° a)   · a = 45° b) b = 40° d) b = 65°
b) Beweise den Tangentensatz: Ist zusätz­
Fig. 1
lich t die Länge einer Tangente von S an 3 Ergänze die fehlenden Seitenverhältnisse.
2
den Kreis, dann ist dieses Produkt gleich t
. a) tan (a) = _
º
b) tan (d) = _
º
º   º   º
Vermischte
cos (b) = _
Aufgaben
º   
tan (c) = _
º
º   
_
Seite 74, Aufgabe 415
cos (d) = _
º
sin (b) = º
º   
º   
Zwei Kreise mit den Radien 2.9 cm und 5 cm haben einen Mittelpunktabstand von Fig. 1
10 cm. Konstruiere alle Geraden, die aus dem ersten Kreis Sehnen von 4.2 cm und gleich­
10
zeitig aus dem zweiten Kreis Sehnen von 6 cm herausschneiden.
4 Wahr oder falsch?
Ergänze die fehlenden Angaben.
Wenn man in einem rechtwinkligen Dreieck mit c = 90°
q
w
a) _
den Winkel a verdoppelt, so verdoppelt sich auch tan (a),
  = tan (º) b) _ r   = cos (º)
v
a) 16 Berechne die Seiten des Dreiecks ABC aus a + b + c = 25 cm und daraus, dass die Win­
p
b) die Hypotenuse halbiert und die Ankathete von a beibehält, so verdoppelt sich cos (a),
kelhalbierende von c die Seite c in einen Abschnitt der Länge 5.1 cm bei A und 3.4 cm bei _
º    = sin (º)
_uv   = º (v) c) die Ankathete von a halbiert und die Gegenkathete von a verdoppelt, so vervierfacht B teilt.
v
_
º
_
sich tan (a),
w   = tan (º) q    = tan (º)
d) den Winkel a vergrössert und die Hypotenuse beibehält, so vergrössert sich cos (a),
17 Konstruiere ein Dreieck ABC mit a : b = 2 : 3, b = 100° und c = 7 cm.
e) 5 den Winkel a verkleinert und die Hypotenuse beibehält, so verkleinert sich tan (a).
Berechne die fehlenden Seitenlängen.
18
a) Übertrage Fig. 2 ins Heft und konstru­
b) c)
11 Zeichne ohne Berechnung der Winkel ein Dreieck ABC mit c = 90°, a = 4.8 cm und
iere alle Kreise, die durch A und B gehen b
Seite 75, Aufgabe 12
2.5 dm
r
x
8.6 km
7.2 cm
a) tan (a) = 1.2; b) sin (a) = 0.6; c) cos (b) = 0.8; d) tan (b) = 1.5.
und g berühren. (Hinweis: Zeige, dass die 56°
36°
g
Tangenten von P an alle Kreise durch A y
c
13.2 km
2
_
12
a) Zeichne ein rechtwinkliges Dreieck mit cos (a) =  
. und B gleich lang sind.) 7
Begründe, dass die gefundenen Berüh­
b) Zeichne ein rechtwinkliges Dreieck mit tan (a) = 1.5.
6 Berechne die fehlenden Seitenlängen und Winkelgrössen.
rungspunkte diejenigen Punkte Q auf der c) Zeichne ein rechtwinkliges Dreieck mit sin (b) = 0.9.
A
B
a) b) c)
15 251 m
17.3 cm
P
oberen bzw. der unteren Halbgeraden von s
17.3 km
r
23°
x
g sind, von denen man AB jeweils unter 13 Ein Mountainbiker überwindet auf einer Fahrstrecke von 500 m einen Höhenunter­
37°
p
y
den grössten Winkeln sieht.
schied von 89 m. Berechne den Steigungswinkel a und die Steigung in Prozent (Fig. 2).
Fig. 2
35.2 km
Die Stei
Strasse
hältnis d
trahiert wird. 2
2
2
2
2
2
a2 = b2Gleichungen
+ c2 – 2 b c ·vom
cos (a),
Lineare
Typ abx =+ ab =+cc – 2 a c · cos (b), c = a + b – 2 a b · cos (c)
y
haben immer dann genau eine Lösung,
y = ax + b
2
2
2
Im Sonderfall c = a + b
wenn
a87,
≠ 0Beispiel
ist.c = 90° Rechnerisch
bedeutet dies,
Seite
1 geht die letzte Gleichung über in: 4 .
Man nennt deshalb den Kosinussatz auch den «verallgemeinerten
Satz des Pythagoras».
dass
der letzte Schritt, nämlich die Division
Aufgaben
3
durch
a, ausführbar ist. Zeichnerisch beMithilfe des Sinus­ und des Kosinussatzes lassen sich fehlende Seiten und Winkel eines deutet
dies,
dass die zugehörige
1Beispiel
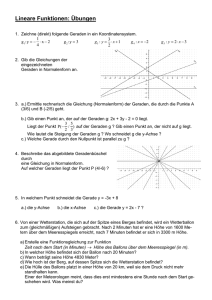
Gib
die Steigung
m und den Gerade
y-Achsenabschnitt b an.
b
beliebigen Dreiecks berechnen, wenn drei Stücke gegeben sind.
ga)
(x)
=
a
x
+
b
eine
von
null
verschiedene
f
(x)
=
0.5
x
+
3
b)
f
(x)
=
2
x
–
1
c)
f
(x)
=
x
d) f (x)y == b1
Löse.
a)
I:
4
x
–
5
y
=
13
b)
I:
2
x
+
3
y
=
4
Mit dem Kosinussatz ergeben sich im Unterschied zum Sinussatz die Winkel eindeutig, denn 1
1 und deshalbII:
Steigung
hat
jeden
beliebigen
4
x
+
5
y
=
3
II:
3
x
+
4
y
=
5
_
e)
f
(x)
=
2
 
x
–
1
f)
f
(x)
=
2
x
–
(1
–
x)
g)
f
(x)
=
2
x
–
(3
+
2
x)
h) f (x) = – 4 + _31  x x
bei einem sich ergebenden positiven (negativen) Kosinuswert ist der Winkel spitz (stumpf).
4
Funktionswert
c annehmen kann.
Lösung:
– 4 – 3 –2 – 1 O
1
2
3
4
Beispiel
1 a = 0 ist,von
Wenn
aber
dann
hat die
zugehöa)
Die
Koeffizienten
y
sind
5
und
–5;
addiert
man
5 y und
–5 y,
man null.
– 1so erhält
2Von einem Dreieck ABC sind Zeichne den Graphen der linearen Funktion. Liegt eine
Proportionalität
vor?
b = 4 cm; c = 7 cm; a = 64° 3 gegeben. Bestimme a, b und c.
rige
Gerade Gleichungen
g (x) = b für alle
x-Werte
nur
Addiere
und
a)
f: x ¥ die
1.5 x + 1
b)I g:
x ¥II.x – 2
c) h: x ¥ _4 x – 1 – 2 d) k: x ¥ 0
Lösung:
einen einzigen Funktionswert, nämlich b
I: 4 x – 5 y = 13
e)
m:1).x Die
¥ –Gerade
1.8 x hat die
f) n:Steigung
x ¥ 1 + null
2.5 x
g)II:
p: x4 x¥+–5xy = 3 – 3 h) q: x ¥ – 3.5 – _21  x
Nach dem Kongruenzsatz sws ist das Lösungsdreieck eindeutig.
(Fig.
2
2
2
2
2
2
a = b
+ c – 2 b c · cos (a) = 16 cm
+ 49 cm
und
verläuft
parallel zur x-Achse. Die
Glei- – 56 cm
I + II: · cos 64° 8 x = 16 – 4 ´ a ≈ 6.4 cm
!:8
sin (b)
b sin (a)
4 cm sin (64°)
3
Zeichne
den
Graphen
der
Funktion
b
chung
0 · hat sin (b) = keine Lösung,
__
sin (a)
 x + b = c ´
_
 
=  
´ b ≈ 34.2°
_a  = _
x
=
2
a
f: x ¥ 1.5
xc– ist.
3 und
gib
eine
g an, 6.4 cm
wenn
Für II)
b =durch
c istFunktion
Wert
Ersetzeb x≠ in
Ib’ = 180° – b ≈ 145.8° (oder
2.jederist wegen der Winkelsumme im Dreieck keine Lösung.)
4 · 2 – 5 · y = 13
!–8
(Der Winkel deren
Graph
zum der
Graphen
von f parallel ist
Fig. 1
für
x eine
Lösung
Gleichung.
–5 · y = 5
! : (–5)
SE84734781_G_K02_053_01.eps
a + b + c = 180° ´ –2
c = 180° – (a + b) = 180° – (64° + 34.2°) ´ c ≈ 81.8°
und
die y-Achse bei
schneidet.
y = –1
Beispiel
1
Das Gleichungssystem
hat die Lösung (2 ! –1).
4b) Multipliziert
Gib jeweils
die
zuI mit
dendie
Bestimme
rechnerisch
und grafisch
manGleichung
Gleichung
3Geraund Gleichung
II mit –2, dann
grafisch
b ergebeny 6 x und –6 x
den
(Fig.
1)
der
Zuordnung
x
¥
y
an,
3
Nullstellen
der Funktionen
bei der anschliessenden
Addition null mit
und die Variable x kommt in der neuen
Gleichung a
1109,
der
sich
der
y-Wert
berechnen
lässt.
Seite
Aufgabe
5
_
a:
x ¥mehr
nicht
vor. und b: x ¥ – 2 x – 1.
2
3  x + 1.4
Fig. 1
Lösung:
I: 2 x + 3 y = 4
! ·3
1
1 und der Punkt Q
_
5
Der
Punkt
P
liegt
auf
der
Geraden
g
mit
der
Gleichung
g
(x)
=
 
x
+
1
rechnerisch:
II: 3 x + 4 y 1= 5 2 ! · (–2)
1
x
1
_ x + 1.4g=
liegt
der Geraden
g2 (x) I:
= –6_23x x ++ 98.y =Der
zu
a: auf
0 der| –Gleichung
1.4
Man
erhält:
12 Punkt R O(5 | 2) liegt auf
2 mit
3
3 –2 –verbindet.
1
1 Bestim2
3
– 6–6–x5Q
1
der horizontalen Geraden
– –miteinander
84y =– –10
_ x = – g
3 , welche
1.4
| : _31   die Punkte PII:und
–1
3
me
den Abstand
zwischen
den II.
Punkten P undI Q.
Addiere
die Gleichungen
und
+ II:
y=2
x = –I 4.2
Ersetze y in I (oder II) durch 2.
2x + 3·2 = 4
! ––26
Durch
man:
Gerade
Die
ist beiAxbis
= –4.2.
6 Nullstelle
In vier Gefässe
D fliesst Öl. Hierbei lässt
sichAblesen
jeweils
die
h (in
cm) ina
2 x = erhält
–2 Füllhöhe
! : 2 Die
SE84734781_G_K02_053_02.eps
schneidet die
bei x ≈ – 4.3,
zu
b:
– 2 xder
– 1Zeit
= 0 t (in s)
| +mit
1 einer Funktionsgleichung
Abhängigkeit
von
x =x-Achse
–berechnen.
1
Seite
113,
3 Beispiel 2 1 die Lösung
diehGerade
DashGleichungssystem
A:
(t) = _2 · t + 2 – 2 x =hat
B: h (t) =| :2(–·2)
t +(–1
2 ! 2). C:
(t) = t +b1bei x ≈ –0.5.
D: h (t) = 3 · t
x = – 0.5
a) Wie
hoch steht
dasx Öl
den Gefässen A und B zu Beginn der Messung?
Die
Nullstelle
ist bei
= –in0.5.
y
grafisch
b) Wie schnell steigt das Öl in Gefäss C?
Aufgaben
3
c) In welchen
Gefässen ist zu Beginn der Messung kein Öl vorhanden?
Beispiel
2
d) In die
welchem
Gefäss
Ölrechneum 2 cm pro Sekunde?
2
Löse
Gleichung
2 xsteigt
+ 2 mit
= das
2.75
1 Bestimme
die Lösung
dem
Gleichsetzungsverfahren.
e)
In
welchem
Gefäss
steigt
das
Öl
am
schnellsten
(langsamsten)?
risch
a) y =und
3 x grafisch.
–6
b) y = x – 4
c) x = –3 y + 7
d) x = 7 y – 8
1
f) Zeichne die Graphen der Zuordnungen Zeit t ¥ Füllhöhe h.
x
Lösung:
y = 4x + 7
y=x+4
x = –4 y + 7
x = 8y – 7
2
_
rechnerisch:
x + 2 =f)2.75
= 16 – xden2Graphen
x + Funktion
y |=–02
g) 3–x4– –y 3=g1(x)
x + 2m
11 ==3_411
y4
–2 =–m
1 xO + bh)1für
7e) y Zeichne
der
5  , b = 1.
– 1 x ≈ 0.4
2 x = 0.75
| :y2= 0.7mit der Gleichung
y
=
x
–
16
x
+
0.4
x
–
y
=
6
x
+
22
=
33
y
Untersuche die Auswirkungen auf den Graphen von g.
x = 0.375
Durch
Ablesen erhält man
a) Kehrwertbildung bei m
b)
Vorzeichenwechsel
bei mx ≈ 0.4.
2
Bestimme
die
Lösung
mit
dem
Einsetzungsverfahren.
SE84734781_G_K02_053_03.eps
c) Vorzeichenwechsel bei b
d) Vorzeichenwechsel bei m und bei b
a) y = 3 x + 8
b) y = –0.5 x + 2
c) 3 x + 2 y = 8
d) 3 y – 6 x = 4
x + y = 12
1.5 x + y = 3
y = 0.5 x – 4
y = 3x – 2
8e) 2.7
Prüfe, ob die Punkte auf der Geraden
mit
der
Gleichung
y
=
–2
x
+
1
liegen.
2
x + 3.2 y = 2.5
f) x = 5 y – _ 
g) 7 y 3= x + 4
h) 5 x – 6 y = 3
a)
P (5 125,
| –9) Aufgabe 3
b) Q (–3 | 6) 5 1
c) R _4  | – _21  
d) S (2.5 | –3.5)
Seite
4 x = 10 y + 6
3y = x – 1
2.7 x = y + 0.4
5 y = 2 x + _3 
2 
Chiwa, Usbekistan, gestorben 1048 in Ghazni,
Afghanistan).
C
3
2 
3
93 Welche
der Punkte A (–4 | –5); B (4 | 0); C (2 | –1.6); D (40 | 27) und E (– 7 | – 9) liegen
Löse mit dem Additionsverfahren.
3
oberhalb, welche unterhalb und welche auf der Geraden mit der Gleichung y = _4 x – 3?
a) 6 x + 7 y = 23
b) 2 x – 3 y = 23
c) 7 x + y = –1
d) 7 x + 5 y = 3
x + 7 y = 18
2 x + y = –13
7x – 2y = 5
7x + 5y = 5
105Gibt
es eine Funktion, welche die x-Achse (die y-Achse) als Graphen hat? Begründe.
e) 7 x + 10 y = 3
f) 6 x – 3 y = 11
g) 9 x – 7 y = 10
h) 13 x + 13 y = 14
2x + 5y = 3
3 x – 1.5 y = 6.5
3x + y = 2
–6.5 x – 6.5 y =7.5
b
α
A
c
B
Hinweis:
Durch Rundungen kön731960_K2_45.1
SY M
nen sich bei verschiedenen Lösungswegen (wie
hier für b) voneinander
geringfügig abweichende Werte ergeben.
87
113
Führe in Aufgabe 8 eine
Punktprobe wie auf Seite 104 durch.
109
125
Seite 134
9 Quadratische Funktionen und quadratische Gleichungen
9.1 Quadratische Funktionen
In der Fahrschule lernt man: Wenn man die Geschwindigkeit in km/h durch 10 dividiert und das Ergebnis quadriert, so ergibt sich der Bremsweg in Metern. Rein quadratische Funktionen
Die Tiefe eines Brunnens kann man bestimmen, indem man zum Beispiel einen Stein in den Brunnen fallen lässt und die Falldauer stoppt.
Hat man die Falldauer t (in Sekunden) gemessen, lässt sich die Fallstrecke s (in Metern) näherungsweise mit der Gleichung s (t) = 5 t2 berechnen. Beträgt die Falldauer beispielsweise 1 s, so ergibt sich für den Brunnen eine Tiefe von s (1) = 5 · 12 = 5, also 5 m, bei einer Falldauer von 2 s eine Tiefe von s (2) = 5 · 22 = 20, also 20 m. Man erkennt: Verdoppelt sich die Falldauer, so wird die Fallstrecke nicht etwa ebenfalls verdoppelt, sondern vervierfacht. Dies liegt daran, dass der Stein beim Fallen beschleunigt wird. Die Strecke, die der Stein während des Fallens in jeweils einer Sekunde zurücklegt, nimmt zu.
Die Gleichung s (t) = 5 t2 gehört zu einer ·(– 2)
rein quadratischen Funktion. Setzt man ·2
·3
·4
für t verschiedene Werte ein, so erhält man die zugehörigen Werte für s. Die t
–2 –1
0
1
2
3
4
Werte paare lassen sich in einer Wertes(t) 20
5
0
5
20
45
80
tabelle darstellen. Man erkennt: Dem 2-, 3- bzw. n-Fachen der ersten Grösse wird ·4
·9
·16
das 4-, 9- bzw. n2-Fache der zweiten Grösse ·4
Fig. 1
zugeordnet.
Überträgt man die Werte in ein Koordinatensystem, so sieht man, dass die Punkte nicht auf einer Geraden liegen. Man darf diese Punkte deshalb nicht geradlinig verbinden.
Den genauen Verlauf des Graphen in Fig. 2 erhält man, indem man durch Einsetzen von Zwischenwerten für t weitere Wertepaare ermittelt.
Ein Graph dieser Art heisst Parabel.
80
70
60
50
40
30
20
10
–2
–1
O
s
s (t) = 5 t 2
t
1
2
3
4
Eine Funktion mit der Gleichung f (x) = a x2 bzw. y = a x2 heisst rein quadratische Funktion. Ihr Graph ist eine Parabel.
134 Fig. 2
1
d) f: x ¥ – 2 x _ 2 ;  (x ≥ 0)
2 In Fig. 1 sind für verschiedene ExpoSeite
146, Merkkasten
nenten z die Graphen der Funktionen x ¥ x z im Ø. Quadranten gezeichnet. a) Welche der Funktionen sind Umkehrfunktionen zueinander? Was kannst du Die Lösungen einer quadratischen Gleichung a x2 + b x + c = 0 sind die Nullstellen der über die beiden Exponenten aussagen?
zugehörigen quadra tischen Funktion f (x) = a x2 + b x + c. Eine quadratische Gleichung b) Welche Punkte haben alle Graphen gehat entweder zwei Lösungen, eine Lösung oder keine Lösung.Fig. 1
meinsam? Begründe.
3 a) Begründe: Die Funktion f: x ¥ 3 x2 – 5 mit der Definitionsmenge R ist nicht umBeispiel
kehrbar. Beispiel 2
2
Bestimme die Lösungsmenge.
b) Ist die Funktion f: x ¥ 3 x
– 5 für x ≥ 0 umkehrbar? Gib in diesem Fall die Gleichung Gegeben ist die Funktion f mit f (x) = 23 x + 5. Schreibe die Funktionsgleichung in der Form 2 – 2.5 x + 2 = 0 2 + 2 x + 2 = 0 Seite
161, Aufgabe 4a) x
0
.5 x
b) – x
c) 1 + x2 = 0
der Umkehrfunktion an und skizziere beide Graphen.
f (x) = b · a .
Lösung:
Lösung:
y
a) Die Normalform lautet x2 – 5 x + 4 = 0. y
4 Entscheide anhand der Graphen in Forme den Funktionsterm um; wende dazu die Potenzgesetze an:
9
5 2
y = x2 + 1
2 – 5 x + 4 = 2 x – _
3 3 x_
3
Wegen x
 
–  
hat die 3 x + 5
3 x
5
5
x
x
2
Fig. 2, ob die zugehörigen Funktionen um4
2
= 2 · 2 = 2 ·   2 2 = 32 · 8
, 5 also f (x) = 32 · 8
.
5
9
zugehörige Parabel den Scheitel S 2 _ 2   | – _ 4   34 . kehrbar sind. Schreibe die Funktionsgleif 4
Am Graphen lassen sich die Nullstellen 3
chung und ggf. die Gleichung der Umkehry = x2 – 5x + 4
Oft interessiert, nach welcher Zeit sich die Wachstumsgrösse verdoppelt bzw. bei x = 1 und x = 4 ablesen. L = {1; 4}
funktion auf.
3
2
Abnahme halbiert hat.
b) Die verschobene Normalparabel hat den g
Verdopplungszeit TD nennt man die Zeit, Halbwertszeit
T2H nennt man die Zeit, in 1
h
Scheitel S (1 1 3) und ist nach unten geöff5 Zeichne den Graphen der Funktion. in der sich der Funktionswert jeweils verder sich der Funktionswert jeweils halbiert.
x
2
net. Die Nullstellen lassen sich nur nähey = – x + 2x + 2 1
Schränke, falls nötig, die Definitionsmenge Beispiel
4
__
doppelt.
O
x
–1
2
– 4 –und 3 – 2x ≈ 2.7.
1
3
4
5
rungsweise ablesen: x ≈ – 0.7 so ein, dass eine umkehrbare Funktion enta) Schreibe lg 2  √x3 3 als Vielfaches von lg (x).
2 –1
O
c) Die Parabel mit der Gleichung y = x
+ 1 –
3
–
2
–
1
1
2
3
4
5
steht. Bestimme dann die Gleichung der b) Schreibe lg (u) – 3 · lg (v) als einen einzigen Logarithmus.
–1
ist eine um 1 Einheit nach oben verscho–2
Umkehrfunktion.
Lösung:
__
3
bene Normalparabel. Sie hat keine Nullstela) Wende das 3. Logarithmengesetz an: f (x) = 0.5 x2 b) f (x) = x2 – 2 lg 2  √x3 3 = lg 2  x _2   3 = _ 32  · lg (x)
–2
–3
2 }.
len, also ist L = { u
c) f (x) = 0.5 x2 – 2 d) f (x) = (x + 1) 2 v3 3 = lg 2 _
b) Wende das 3. und das 2. Logarithmengesetz an: lg (u) – 3 · lg (v) = lg (u) – lg v3  3 –4
e) f (x) = (x – 3) 2 f) f (x) = 2 (x – 1) 2
Lösungsformel für quadratische Gleichungen
–1 6 Zu welcher Funktion f ist f die Umkehrfunktion?
Aufgaben
__
1 –1
–1
–1
Fig. 2
3
Die Lösungen quadratischer Gleichungen kann man zeichnerisch oft nur näherungsweise a) f : x ¥ √ ____
x b) f : x ¥ x _4  
c) f : x ¥ x _ 2  
d) f –1: x ¥ x – 1
–1
–1
–1
2
–1
bestimmen. Die exakten Lösungen können dann nur rechnerisch ermittelt werden.
√
e) f : x ¥ 
x – 2 f) f : x ¥ x g) f : x ¥ x
h) f : x ¥ (x – 2) 2
Beispiel zu Aufgabe 1:
1Seite
Schreibe als Logarithmus wie im Beispiel auf dem Rand.
174, Beispiel 3
2  3– 3
25 = 32 ; 5 = log (32)
1
2
_
a) 43 = 64 b) 72 = 49 c) 3– 2 = _ 91  
2d) 3   = 27
__
Eine quadratische Gleichung in Normalform x
+ p x + q = 0 kann man durch quadra7 Umkehrfunktionen bei linearen Funktionen
– 6
1
y
0.5
0
Beispiel
Bei36
der Reaktorkatae) 1000
 
h) x = z
= 6 f) 8 = 1 3
g) 2   √10 3 = _
tische Ergänzung lösen.
a) Gib deinem Nachbarn die Gleichung einer linearen Funktion und lasse ihn die Gleistrophe
von Tschernobyl
a) Cäsium 137 hat eine Halbwertszeit von 33 Jahren. Gib den Wachstumsfaktor für ein 2
x + p x + q = 0 | – q z. B. x2 + 5x + 6 = 0 | – 6
chung der zugehörigen Umkehrfunktion bestimmen.
im
Jahr 1986 wurde
Jahr an. Wie viel Prozent beträgt die jährliche Abnahme?
2
2neben
Schreibe als Potenzgleichung wie im Beispiel auf dem Rand.
x + p x = – q x2 + 5 x = – 6 Beispiel zu Aufgabe 2:
Jod 131 vor allem
b) Zeichne die Graphen beider Funktionen in ein Koordinatensystem. Kannst du so überb) Zu Beginn einer Beobachtung sind 250 mg Cäsium 137 vorhanden. Bestimme die Expolog4 (16) = 2 ; 42 = 16
a) log
(125) = 3 b) log
(0.2) = – 1 c) log
(5) = 1 d) log
Cäsium
5137 freigesetzt.
5
5
5 (1) = 0
prüfen, ob die Gleichung der Umkehrfunktion richtig bestimmt ist?
p
5 2
nentialfunktion, die den Zerfall von Cäsium 137 mit diesem Anfangswert beschreibt.
e) f) log0.2 (0.04) = 2 g) lo g √__2 (0.25) = – 4 h) log
2 _ 2   3 2 auf beiden Seiten der Addiert man Addiert man 2   3 auf beiden Seiten der 0.5 (8) = – 3 b (a) = c 2 _
c) log
Betrachtet gemeinsam weitere Beispiele. Bestimmt dann allgemein zur linearen FunkLösung:
Gleichung, so kann man auf der linken Gleichung, so kann man auf der linken tion f: x ¥ m x + b; (m ≠ 0) die Gleichung der Umkehrfunktion f –1.
a) Der Zerfall des Cäsiums wird durch eine Funktion f mit f (x) = b · ax beschrieben.
3 Bestimme den Logarithmus. Begründe dein Ergebnis.
Seite eine binomische Formel anwenden. Seite eine binomische Formel anwenden.
__
1
TH
Nach der Halbwertszeit T
gilt: b · a (7)
= _   b
2 3
a) log2 (64) b) lg (1) c) Hlog
d) log
3   √ 3 7 2
11
33
1
1
1
_   _
161
Einsetzen der gegebenen Halbwertszeit: b · a g = __ 2
e) log _
  f) log _
__   g) log _
3 __   h) lo b
  2  3
2 16
146 4
Bestimme.
a) loga (a) 5 2  3
5 √ 5 6
2  6 3
√ 2  3
1
√ 6 6
_
a33 = _ 1 ;  a = _ 1   33   ≈ 0.979
3
2  3
Daraus folgt (da b ≠ 0): 2
2
Aus a ≈ 0.979 (= 97.9 %) ergibt sich eine jährliche Abnahme von etwa 2.1 %.
1
1
2 n3
_
b) logb) Anfangswert: c) logb = 250 (mg); d) log
e) an   x loga _
a (1) a 2  a   3 a   a f (x) = 250 · 0.979
2  3
Berechne a bzw. b. Aufgaben
___
3
1
a) logb (25) = 2 b) logb _
49
  = – 2 c) logb (16) = – 4 d) logb 2  √125 3 = _ 2  
Seite
179,
Aufgabe
6
e) log3 (a) = 4 f) g) log9 (a) = 1.5 h) lg (a) = – 4
1 log
Der Graph einer Exponentialfunktion f mit f (x) = ax verläuft durch den Punkt P. 4 (a) = 3 Bestimme a und gib an, ob die Funktion zu- oder abnimmt.
6 Schreibe als Summe oder Produkt «einfacher» Logarithmen.
a) P (1 1 3) b) P (1 1 0.25) c) P (2 1 6) 2
d) P (– 1 1 3)
3
a) lg (3 x) b) loga (a b c) c) lg 2 u2 3 d) loga 2 2 a b
__ 4
5 e
u v
_
e) loga _
f) g) lg 2  9_
x   3 h) loga 2  √ b 3 a 2  w   3 2 log
Zeichne den Graphen der Funktion f mithilfe einer Wertetabelle. Zeichne dann den f   2  3
2  3
2  3
x2 y3
u2 v3   i) loga _
7 2 
3
2  3
______
r2 s t4
Graphen von g durch Multiplikation der Funktionswerte von f mit dem Streckfaktor.
_   j) loga _
a2 b14 cx7   k) log
l) loga 2  √a11 b3 c5 3 2 u3 v x
a) f (x) = 1.2 ; g (x) = 3 · 1.2 b) f (x) = 0.4x; g (x) = 5 · 0.4x c) f (x) = 2x; g (x) = 0.3 · 2x
Schreibe als einen einzigen Logarithmus.
3 Die Graphen in Fig. 1 gehören zu Exponentialfunktionen f mit f (x) = ax. 2 23
a) lg (x) + lg (2 y) b) log
c) loga (a b) – loga 2 a2 b 3 a  u – loga (u) 2
u
Grösse mit x, so ergibt sich f
Zur Erinnerung:
: x ¥ loga (x).
Von
Punkt A (xA | yf–1 zA ) gelangt man
=x
aloga (x)einem
A |heisst Logarithmusfunktion. Die zuge- x
8 aeinem
(aLöse die Gleichung wie in Beispiel 3, also ohne Taschenrechner.
) = x Punkt B (xB | yB | zB ) indem man
log
zu
Aufgaben
hörige Funktionsgleichung lautet log
(x) = 2 log (3) –1 derb) lg (x) = lg (6) – lg (3) c) lg (x) = 2 lg (5) + 3 lg (2)
xa) –
x
x‑Achse,
B
Aa Einheiten ain Richtung
–2 _
f (x) = log
1 Spiegelt man den Graphen _›
2
_
a (x). › y‑Achse,
›
d) 3 log
(x) = 27 e) 2 lg (x) = lg (16) + lg (9) f) loga (b x) = 1 + loga (5)
179,
Aufgabe
9
ySeite
–
y
Einheiten
in
Richtung
der
a
1
A
1B Berechne
für die Vektoren
a = 2 , b=
, c = 1 :
der Exponentialfunktion an der ersten B (4|5|3)
3
–1
1
zB – zA_Einheiten in Richtung
der
z‑Achse
Winkelhalbierenden, so erhält man den _› _
_› ›
_› _2›
_› _› _›
_› _›
›
9 a a) geht.
·bDer Logarithmus von a
b) a · c zur Basis b ist c. Wie gross ist der Logarithmus c) a ·( b – c )
d) ( a + b )·( b – c )
a)
Graphen der zugehörigen Logarithmus6
A (3|2|1)
Also
der Verbindungsvektor
zwischen
von ahat
zur Basis b?
funktion (Fig. 1). ___› __›
1
_
den
Punkten
A
und
B
die
Koordinaten:
b) Betrachte die Gleichung log
(k·a) =  
b. Drücke k durch a aus, wenn b = logc (a) gilt.
c
2 Gegeben ist ein gleichseitiges
Dreieck
2 ABC. Bestimme AB ·AC .
2  3 2  3 2  3
2  3
Fig. 1
xB – xA
_›
_›
v = AB = yB – yA (vgl. Beispiel in Fig. 1). _›
3 Berechne
den
Zwischenwinkel
v
von
a
und
b , wenn folgende Beziehungen gelten.
Fig. 1
z
–
z
B›
A
_
_›
_
_
_ _›
___›
›
› Die Logarithmusfunktion ›
x ¥ log (x) (a > 0, a ≠ 1) ist die Umkehrfunktion der Expo-
a
a) | a | =180,
3, _|bEigenschaften
| = 4 und ( a –_0.5 der
b ) © Logarithmusfunktion
( a +_b )
Seite
x
_›
_› nentialfunktion _›
›
›
› x ¥ a . Sie ist nur für positive x-Werte definiert.
b)Für
| a |den
= 2|Verbindungsvektor
b_| > 0 und ( a + b )·_zwischen
( a + 3.5·_zwei
b ) = 0Punkten A (xA | yA | zA) und B (xB | yB | zB) gilt:
_›
2  3
2  3 2  3
c) | a | =
_›
›
4, ___
|b ›|
_›
›
B – xA| a – 2 b | = | a + b |
= 6xund
AB = yB – yA Eigenschaften der Logarithmusfunktion:
_›
zB – zA
4
179
›
z
_›
zB
Berechne die Grösse
des
Winkels
Für a > 1 gilt: zwischen den Vektoren a und b .
B(x B | y B | z B)
1
–11 _›
1
5
1
5
– D
ie Funktionswerte nehmen zu, wenn x _
_›
_›
_›
_›
›
.
Der
Verbindungsvektor
zwischen
dem
Koordinatenursprung
O
(0
|
0
|
0
)
und
einem
3
1
4
2
3
3
0
O
a) a =
b) a =
, b=
, b=
c) a =
, b=
grösser wird. Die Funktion ist zunehmend.
1
1
1
3
5
3
xB
xB – 01
yB y
___
1
– Der Graph verläuft für x > 1 über der x›
yB – 0 = yB (Fig. 2).
xB
Punkt B (xB | yB | zB) hat dieAchse, für Koordinaten
OB
=
0 < x < 1 unter der x-Achse.
x
zB z
zB – 0
.
Fig. 2
___› die Längen
5 Berechne
Seiten und
– Fder
ür x ¥ • gilt loga (x) ¥ •, für x ¥ 0 Der
Vektor
OB
heisst
Ortsvektor
des
Punktes
B.
Der
Punkt
B
und
sein
Ortsvektor
besit
zen
die Grössen der Winkel im
Dreieck
ABC.
gilt loga (x) ¥ – •.
dieselben
kann man
a) A (2 | 1),Koordinaten.
B (5 | –1), C (4Daher
| 3) 0 < a < 1 Für gilt:die Koordinaten eines Punktes bestimmen, indem
man
die
Koordinaten
seines
Ortsvektors
berechnet.
___
b) A (8 | 1), B (17 | –5), C (10
9)
– D› |ie Funktionswerte nehmen ab, wenn x Der Verbindungsvektor ABgrösser wird. Die Funktion ist abnehmend.
zwischen
Punkten
___› A und B ist als Differenz der Orts‑
___›den___
›
vektoren
von
A
und
B
darstellbar:
AB
=
OB
–
y
6 Berechne zu Fig. 1 die
Längen
Sei‑ OA
– Für x > 1 der
sind die Funktionswerte nega_›
Fig. 2
ten und
dieBetrag
Grössen
derVektors
Winkel
tiv, für a 0 < x < 1 sind sie positiv. versteht
Unter
dem
eines
_›
a) des Dreiecks
ABC,
log
Für x ¥ • Pfeile.
gilt loga (x) ¥ – •, für x ¥ 0 gilt loga (x) ¥ •. Fig. 1
a(x)
man
Länge
der
zu a– gehörenden
log 1 (x)die
=_
_›
1   _›
_ 3
loga2 von
b) ades
Dreiecks
a
Für beliebige Werte von a (a ≠ 0, x a ≠ 1) gilt:
Der
Betrag
aEDF.
wird mit
| a | bezeichnet.
_›
loga(x)
loga(x)
– A
lle Graphen von f mit f (x) = log
Kennt
man
die
Koordinaten
des
Vektors
a
,
a (x) verlaufen durch den Punkt P (1 1 0).  
=_
=_
–1  
a(a) Viereck
7– log
Ein
hat die
Eckpunkte
(0 | 0 | 0), P (2 | 3 | 5), Q (5 | 5 |f (x) = log
6), R (1 | 4a (x) | 9). an der x-Achse, so erhält man den – Spiegelt man den Graphen von f mit so
kann
man seinen
Betrag
mithilfeO des
Längen berechnen
derGraphen von g mit Seiten(vgl.
undFig.
die3).Grössen
der Innenwinkel
des
Vierecks.
=Berechne
– loga(x)
g (x) = – log
(x) = l
og (x) (Fig. 2).
Satzes
von die
Pythagoras
a
_
a1  
Einen Vektor mit dem Betrag 1 nennt man
_› _›
8 Bestimme
die
fehlende
Koordinate
so, dass a © b .
Einheitsvektor.
Man
erhält den
Einheits‑
__
_›
180 ›
1
2
–1 _›
3
_
_›
vektor
a
eines
beliebigen
Vektors
a
_
_›
›
x
_› _› _› 20
1 a› =_› y , b = –1
4 , b = 0
Merkkasten
a)
,
b
=
b)
a
=
c)
_
_
(Seite
a ≠a o=)219,
aus
der
Beziehung
a
=
 
·
a
.
›
3
–4
2  3 2  3
2  3 2  3
2  3 2  3
2  3 2  3
2  3 2  3
_ 
2  3
2  3
0
|a |
3
1
2  3
9
_› _› _›
2
z
Fig. 3
2  3
Der Quader in Fig. 2 wird
a ,_b , c aufgespannt.
__
a_ den
_›_› _ von
__›› _ _
__›› _ax
›
_› Vektoren
2› + a2› ; _
› x› gilt:
› 00000000000000000
›
a
=
|
a
|
=
a
für
a += c›aysind
a2x + a2y + a2z
Betrag
eines
Vektors:
für
gilt:zu| aa|› =orthogonal?
9
90000000000000000000000000000
a
x +
y, a + b
a) Welche der Vektoren b , c , by + c , b
–
c
,
a
b
_
_›
›
az
b) Welche der Vektoren aus a) sind zu a und zu b orthogonal?
_›
_› _›
Sind
Koordinaten
zweier Vektoren a
_die
10
›
_› sind zwei Vektoren a und b . Beschreibe die Lage aller Vektoren, die zu
_› Gegeben
und
b
bekannt,
kann
man
auch
die Sum‑ dabei zwei Fälle:
_
a und
b› orthogonal
sind.
Unterscheide
›
_›
_›_› zu_›_
_›
Seite
229,
Aufgabe
11
me
c
=
a
+
b
in
Koordinaten
angeben.
a) a und b sind linear unabhängig,
b) a und b sind linear abhängig.
Fig. 4 entnimmt man:
5
3
Normalenvektor
von a und b.
2 1121 3 +Bestimme
2 –23 3 = 2 21 –+einen
2 3 = 2 –1 3
_
_
2  3 2  3
1
_
2
›
_
2  3 2  3
2
_
5
›
›
›
›
sich
Die
a) aKoordinaten
= 2 , b =von0 c ergeben b)
a› =aus3_› , b = –1
_
den Summen
der Koordinaten
von a und–1b .
3
–2
3
2  3 2  3
1
c
b
a
Fig. 2
4
c) a = 2 , b = –1
5
5
Fig. 4
219
229
Seite 236, Einstieg
15.2 Geraden in der Ebene
y
Welche der folgenden Geraden sind D
in der Grafik dargestellt?
2  3 2  3
2  3 2  3
_›
_›
3 g1: r = 1 + t –2 g2: r = 4 + t 1 0
1
3
g3: y = – _ 23  x + _ 37  
g4: 2 x + 3 y = 11 3
A
2
B
1
x
O
1
2
3
Gleichungen von Geraden
4
5
y
B
2
Seite 241, Beispiel Die Parametergleichung der Geraden in der Ebene besitzt gegenüber der Parame1
tergleichung im Raum keine z-Koordinate.
A
Beispiel Gegenseitige Lage von Geraden
Die Gerade in Fig. 1 durch die Punkte –3 –2 –1
Bestimme die gegenseitige Lage der Geraden g und h.
A (–3 | 0) und B (3 | 2) mit A als Stützpunkt _ __›
3 1 2 4 1 4 2 7 und Zur Erinnerung:
_›
_› AB als Richtungsvektor hat die _›
_›
4 , h: r = 6 + t · _
8 › –3 b) g: r = –2 + s · 3 , h: r = –6 + t · 1 2 a) g: r = + s · Zwei Punkte legen
Parameterform r = 6 4
2
1
2 0 + t· . 2
3
–1
1
2
eindeutig die Funktions-
2  3 2  3
2  3 2  3
2  3 2  3 2  3
2  3 2  3
2  3 2 
3 2  3
2  3 2  3
6
x
1
2
3
Fig. 1
gleichung
einer
_
31  x + 1 1 3 Geraden4 Diese Gerade kann ebenfalls als Graph einer linearen Funktion mit der Gleichung y = –4 _›
_›
fest
(vgl.
S.
110).
r = 0 + t · –6 c) g: r = 6 + s ·
8 , h: beschrieben werden oder, äquivalent dazu, durch die Koordinatengleichung – x + 3 y = 3 2
3
4
2
(vgl. Kap. 8.1).
Lösung:
Sonderfälle:
Da in a) die Richtungsvektoren Vielfache voneinander sind, können g und h entweder parx-Achse:
y=0
allel sein oder identisch. Eine Punktprobe muss durchgeführt werden. In den Teilaufgaben Die Gleichung a x + b y = c heisst Koordinatengleichung der Geraden in der Ebene. Day-Achse:
x=0
b) und c) sind die Richtungsvektoren keine Vielfachen voneinander, die Entscheidung bei ist mindestens einer der Koeffizienten a und b von 0 verschieden.
zwischen Schnittpunkt oder windschief muss durch Lösung der Vektorgleichung gefällt Parallele
zur x-Achse:
Die Gleichung der Form x = c gehört zu einer Parallelen der y-Achse. In diesem Fall gibt es ywerden.
=c
a) Der Ortsvektor des Punktes P (3 | 6 | 4) der Geraden h wird in die Geradengleichung der keine Funktionsgleichung der Geraden.
Parallele
zur y-Achse:
2  3 2  3 2  3
3 x=c
1 2 6 = 2 + s · 4 ergibt s = 1. Geraden g eingesetzt. Die Punktprobe Beispiel 1 Von der Parametergleichung zur Koordinaten- und Funktionsgleichung 3 1 4
_›
2  3
2  3
Bestimme die Funktions- und Koordinatengleichung der Geraden r = 1 + t · –2 . 5
–3
Damit liegt der Punkt P auf der Geraden g. Die beiden Geraden sind identisch. Lösung:
4 2 _›
1 7 Die Steigung m der Geraden lässt sich direkt aus dem Richtungsvektor u ablesen (Fig 2): Tipp:
–6 3 1 b) Der Vektorgleichung –2
–2 5 + s · 51 = –1 + t ·
2 entspricht das lineare Gleichungs5 Gleiu=
Zur
Lösung des
2
_
_
_
m = –2  = – 2   . Durch Einsetzen der Koordinaten des Stützpunktes P (1 | –3) in y = – 2   x + b 5
5
chungssystems
betrach5
1
1
_
_
ergibt sich b = – 2   . Man erhält somit die Funktionsgleichung y = – 2   x – _ tet
7 + 2 s = 4 + t 2 s – t = –3 2   und äquivalent man zunächst zwei
bzw. 3 s – t = –4 . System (LGS) – 2 + 3 s = –6 + t der drei Gleichungen,
dazu eine Koordinatengleichung 5 x + 2 y = – 1.
2  3 2  3 2  3 2  3
((
{
–2
2 + s = –1 + 2 t
{
s – 2 t = –3
um die Lösung zu berechnen.
Anschliessend führt man
in der dritten Gleichung
die Probe durch.
g
Beispiel 2 Von der Funktionsgleichung zur Parametergleichung
Fig. 2
Dieses LGS hat die einzige Lösung s = – 1; t = 1. Also schneiden sich g und h. _ 2   x + 2 .
Bestimme eine Parametergleichung der Geraden g: y = 3
7 2 5 Lösung:
_›
_
3 ›
3 für s die Zahl –1, so erhält man den Vektor Setzt man in –2 + s ·
s = –5 . u = 2 von g kann aus dem Steigungsdreieck abgelesen werden Ein Richtungsvektor 2
1
1
(Fig. 3), und ein möglicher Stützpunkt ist der Schnittpunkt mit der y-Achse S (0 | 2). Somit schneiden sich g und h im Punkt S (5 | –5 | 1). 2  3 2  3
2  3
2  3
2  3 2  3 2  3 2  3
{ _›
2  0 3 2  3 3
3 + 4 s = 1 – 4 t 4 1 –4 3 Daraus ergibt sich die Parameterform der Geraden g: r = 2 + t· 2 8 = 0 + t · –6 entspricht das LGS 6 + 8 s = – 6 t c) Der Vektorgleichung 6 + s ·
.
2 3 4 + 2 s = 3 + 2 t
Fig. 3
4
2
Dieses LGS hat keine Lösung. Also sind g und h windschief zueinander.
Spurpunkte
und spezielle Lagen von Geraden
236 Im Allgemeinen durchstösst eine Gerade g alle drei Koordinatenebenen. Diese Durch-
z
g
Syz
Die von den Koordinatenachsen aufgespannten Ebenen nennt
man Koordinaten­
ebene.
1
–3 – 2 – 1
4
3
2
3
4
5
0
–3 –2 –1
–2
–3
Seite x252, Aufgaben
11 und 12
2
Fig. 1
x
1
1
2
3
4
5
Fig. 2
11 Wie kann man an der Ebenengleichung erkennen, dass zwei Spurgeraden zueinander parallel sind? Zeichne die drei Spurgeraden und schraffiere einen Ebenenausschnitt.
a) E: 4 x + y = 8 b) E: 2 x – 3 z = 6
12 Gegeben ist die Ebene E: 3 x + 4 y + 6 z = 0.
a) Begründe: Die Spurgeraden gehen alle durch den Ursprung.
b) Zeichne die Spurgeraden. Gib mithilfe von Parallelen zu den Spurgeraden einen Ebenen - ausschnitt an.