LK 11.2 1996/97

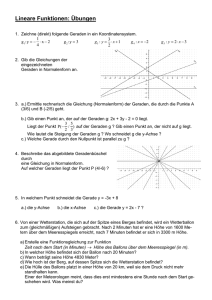
2003/04 , 12.2 , LK Mathematik
Bonn, den 02. April 2004
Übungsaufgaben Nr. 4
1. (Buch, S. 18, 6) Man bestimme die Gleichung einer Ebene, die den angegebenen Bedingungen
genügt. Die Ebene
(a) ist parallel zur xz-Ebene ;
(b) geht durch (2|-1|4) und eine der Koordinatenachsen ;
(c) ist parallel zur z-Achse und geht durch (4|0|0) und (0|3|0) ;
(d) ist parallel zur x-Achse, geht durch (0|3|0) und ist außerdem parallel zur Geraden, die diagonal
im I. Quadranten verläuft ;
(e) ist senkrecht zur y-Achse und geht durch (1|1|1) ;
( f ) ist senkrecht zur Geraden, die diagonal durch den I. Quadranten verläuft, und geht durch den
Ursprung. (c) Man berechne mit TR die Potenz p = 2 2 mit TR und ebenso die Potenz p 2. Es
ist bis heute nicht bekannt, ob die Zahl p rational oder irrational ist. Unter Berücksichtigung dieser
Unkenntnis ist es dennoch möglich, zu beweisen, dass es eine Potenz gibt, die rational ist,
obwohl Basis a und Exponent x selber irrational sind. Man führe diesen Beweis.
2. (Buch, S. 18, 10) Man berechne die Gleichung einer Ebene durch die angegebenen Punkte A, B, C.
(a) A(0|2|2), B(-4|0|1), C(4|2|0)
(b) A(5|3|1), B(0|6|-6), C(-5|0|1)
3. (Buch, S. 17, 3) Gegeben ist die Ebene mit der Gleichung
2
3
 : z = 3x+4y-1.
(a) Man zeichne die Ebene .
(b) Man prüfe, ob die Punkte P(1|1|1), Q(3|-4|-2), und R(-6|-12|6) in der Ebene  liegen oder, bezogen auf die xy-Ebene, darunter oder darüber.
(c) Man berechne, wo die Ebene die Koordinatenachsen schneidet und welche Gleichungen die
Geraden haben, die die Ebene aus den Koordinatenebenen ausschneidet.
(d) Wo schneidet  die Gerade, die diagonal durch den I. Quadranten verläuft ?
4. Man führe eine Kurvendiskussion durch und bestimme das Integral der folgenden Funktionen:
4. Gegeben sind die Punkte A(-2|1|4) und B(6|2|3).
(a) Welche Gleichung hat die mittelsenkrechte Ebene zur Strecke AB ? Welche Punkte auf den
Koordinatenachsen sind gleich weit von A und B entfernt ?
(b) Gesucht ist ein Punkt C auf der z-Achse, dessen Abstand von A halb so groß wie sein Abstand
von B ist.
5. Gegeben sind die Punkt A(-1|3|2), B(0|1|4) und C(3|1|-2) .
(a) Man zeige, daß der Winkel BAC ein Rechter ist.
(b) Man bestimme einen Punkt D, so daß das Viereck ABCD ein Rechteck ist.