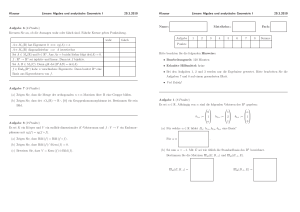
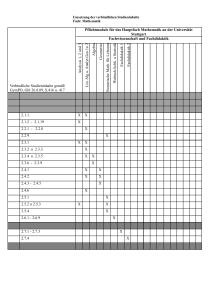
Lineare Algebra: Verständnisaufgaben

!
!
#
#
(
+
+
1
2
!
#
#
##
##
#
,
!
#
#
##
# #
!
.
78
!
#
"
#
%
)
#
# %# -
#
&
3
.
/
.
2#,
/
$
##
$
,
# 1% "
!
)#
!
5
$
!
##
#
#
3
#
#
+
&
#
'
*
#
0
#
!
"
!
'
!
#
)
!,
!,
#
$
##
#
&
$
1
4
##
'
$ #
#
%
6
#
&
1) Multiple Choice: (24 P.)
Kreuzen Sie alle richtigen Antworten an. Beachten Sie, dass es mehrere richtige Antworten geben
kann. Die Bewertung jeder der Teilaufgaben geschieht folgendermaßen:
Anzahl aller Antworten
Für jedes korrekt gesetzte Kreuz gibt es
viele Punkte. Weiterhin
Anzahl der richtigen Antworten
werden für jedes falsch gesetzte Kreuz 2 Punkte abgezogen. Macht man nur falsche Kreuze, so
kann es durchaus negative Punktzahlen geben. Die Summe der insgesamt erreichbaren Punkte
dieser Teilaufgabe kann durchaus negativ sein.
Beispiel:
-
Welche Aussage ist richtig? Der abgebildete Zug ist …
ein Fahrzeug der Berliner S-Bahn.
ein Fahrzeug der Berliner U-Bahn.
ein Fahrzeug der Londoner U-Bahn.
die Nord-Ostsee-Bahn von Westerland (Sylt) nach Hamburg Altona.
noch nicht in Betrieb.
ein ICE nach Tating.
Hinweis: Hier ist nur eine Aussage richtig und wird mit 12P. bewertet. Falls noch weitere Aussagen
angekreuzt würden, gäbe es pro Kreuz minus 4 Punkte.
1
I.
Welche der folgenden Aussagen sind wahr? Es sei die Ausgangsaussage: „Hannover 96
ist deutscher Meister der Saison 2010/2011“ gegeben. (6P)
O (a) Die Ausgansaussage ist ein sinnvolles sprachliches Gebilde, welches falsch ist.
O (b) Die Ausgangsaussage ist wahr.
O (c) Die Ausgangsaussage ist wahr oder ein sinnvolles sprachliches Gebilde.
O (d) Die Ausgangsaussage ist wahr und ein sinnvolles sprachliches Gebilde.
O (e) „1 + 2 = 2 + 1“ ist ein Axiom.
O (f) „1 + 2 = 2 + 1“ ist ein bewiesener mathematischer Satz.
II.
Welche der folgenden Aussagen sind wahr? Es sei die Aussageform: „2 + x + y =12“
mit den natürlichen Zahlen als Trägermenge für x und y gegeben. (6P)
O (a) Die Aussageform ist ein wahres sprachliches Gebilde.
O (b) Die Trägermenge für x sind ebenfalls die reellen Zahlen oder die Aussageform ist ein
sprachliches Gebilde.
O (c) Die Aussage „
“ ist wahr.
O (d) Die Aussage „
“ ist wahr.
O (e) Die Aussage „
“ ist wahr.
“ ist wahr und die Aussage
O (f) Die mathematische Aussage „
„
“ ist die Negation der Aussage „
“.
III.
Welche der folgenden Aussagen sind wahr? Es sei die verknüpfte Ausgangsaussage A
„Wenn Svenja zur Uni geht, dann geht Matthias ins Kino.“ gegeben. (6P)
O (a) Es handelt sich bei der verknüpften Aussage „Svenja geht ins Kino oder ins Theater.“
um eine Konjunktion.
O (b) Es handelt sich bei der verknüpften Aussage „Svenja geht ins Museum und ins
Theater.“ um eine Konjunktion.
O (c) Die zusammengesetzte Aussage „Svenja geht genau dann ins Kino, wenn das Wetter
schlecht ist.“ nennt man eine Bijunktion
O (d) Die zusammengesetzte Ausgangsaussage A nennt man eine Subjunktion.
O (e) Die hinreichende Bedingung in der Ausgangsaussage A ist, dass Svenja zur Uni geht.
O (f) Die notwendige Bedingung in der Ausgansaussage A ist, dass Matthias ins Kino geht.
2
IV.
Welche der folgenden Aussagen sind wahr? Es sein die Aussagen A, B und C gegeben.
(6P)
O (a) Die Aussage „
“ ist dann wahr, wenn mindestens eine der Aussagen A, B
oder C wahr ist.
“ ist dann wahr, wenn alle Aussagen A, B und C falsch
O (b) Die Aussage „ ¬
sind.
O (c) Die Aussage „
“ ist stets wahr, wenn A falsch ist.
O (d) Die Aussage „ ( A C ) ⇔ (¬A ∨ C ) “ ist falsch.
O (e) Um die Aussage B zu beweisen, genügt es, aus ¬ B einen Widerspruch herzuleiten.
O (f) Nach dem Kontrapositionsgesetz ist die Aussage „ ( A → C ) ⇔ (¬C → ¬A) “ wahr.
2) Naive Logik und Quantoren (14 P.)
a) Formulieren Sie die Aussage „Zu jedem reellen a gibt es ein reelles b und c, sodass a = b + c
gilt“ in formaler Sprache mit Quantoren. (3P.)
b) Begründen Sie, ob die Aussage aus Teilaufgabe a. wahr ist! (1P.)
c) Formulieren Sie die Negation der Aussage aus Teilaufgabe a.! (3P.)
d) Ist die Aussage „
⇔ ! " ! wahr? (1P.)
B ) ∧ ( B C )) ( A C ) “! (4P.)
e) Beweisen Sie die Aussage: „ (( A
f) Prüfen Sie begründet den Wahrheitsgehalt der letzten Aussage! (2P.)
„Svenja und Matthias oder Rebekka und Matthias oder Daniel oder Kay waren die Täter.
Kay und Matthias sind nicht die Täter. Also ist Svenja oder Rebekka der Täter.“
3) Eine Wahrheitstafel (8 P.)
Vervollständigen Sie folgende Wahrheitstafel sinnvoll!
O
w
w
w
f
w
f
f
w
H M
- w w
w f
f w
w w
f f
f w
w f
w w
O∧H
-
H ∧M
-
O∧H ∧M
-
(H ∧ M ) ∨ O
-
(¬( H ∧ M ) ∨ O )
-
H
¬(O ⇔ H )
-
M
Meine Literaturempfehlungen und Quellenangaben:
- Das Skript zur Vorlesung;
- Jänich: „Lineare Algebra“ (10. Auflage) [270 S.]
- G. M. Gramilch: „Lineare Algebra“ (2. Auflage) [200 S.]
- H. Anton: „Lineare Algebra“ [684 S.]
- Hans Altendorfere: „Lineare Algebra und Analytische Geometrie“ (1. Auflage) [280 S.]
- T.S. Blyth and E.F. Robertson: „Further Linear Algebra“ [230 S.]
- Modler/ Kreh: „Tutorium Analysis 1 und Lineare Algebra 1“ [365 S.]
- Fischer „Lineare Algebra“ (17. Auflage) [384 S.]
sowie viele weitere Bücher auf Anfrage!
3