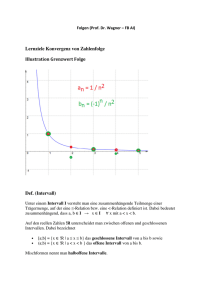
Folgen, Reihen und Grenzwert

Folgen, Reihen und
Grenzwert
Vorlesung zur
Didaktik der Analysis
Inhalt
•
•
•
•
•
Motivation
Folgen
Spezielle Folgen
Grenzwertdefinition
Wichtige Zusammenhänge und Strategien der
Konvergenzuntersuchung
• Funktionengrenzwert
• Reihen
• Paradoxien und Zusammenfassung
Oliver Passon
Folgen, Reihen, Grenzwert
2
Grenzwertbildungen sind charakteristisch für die
Analysis. Im Kern handelt es sich um
Approximationen, die mit formalen Mitteln „zu Ende
gedacht werden“.
Etwa sind alle irrationalen Zahlen nur als Grenzwert
erklärt! Zu seiner Einführung dient der Begriff der
Folge:
Eine Folge ist eine Abb.
a:Ν → R
n a an
Bsp. :
1,1,1,1L : an = 1
1, 12 , 13 ,L : an =
1
n
a0 = 1, an +1 = 1 + an
Oliver Passon
Folgen, Reihen, Grenzwert
3
Spezielle Folgen:
Arithmetisches Mittel:
A(a, b) =
Geometrisches Mittel:
G (a, b) = ab
Harmonisches Mittel:
2
H (a, b) = 1 1 = A−1 (a, b)
a + b
a +b
2
Man nennt Folgen arithmetisch, geometrisch bzw.
harmonisch, wenn (bis auf das erste) jedes Glied entsprechendes Mittel seiner Nachbarn ist.
Oliver Passon
Folgen, Reihen, Grenzwert
4
Beispiele:
• (n)
• (qn)
• (1/n)
Oliver Passon
arithmetische Folge
geometrische Folge
harmonische Folge
Folgen, Reihen, Grenzwert
5
Die Folge an=1/n nähert sich offenbar immer weiter der 0.
Man sagt „Null ist Grenzwert dieser Folge“ oder „die Folge
konvergiert gegen Null“.
Betrachte folgendes Beispiel: an = n ⋅ q mit : k = 10, q = 0,8
k
n
a1 = 0,8
a2 = 655,36
a3 = 30233,088
M
Frage: Hat diese Folge einen Grenzwert?
Offensichtlich muss der Begriff präzisiert werden!
Oliver Passon
Folgen, Reihen, Grenzwert
6
Intuitiv: Folge konvergiert gegen einen Wert a, wenn
Die Folgeglieder der Zahl a beliebig nahe kommen.
Hier fehlt die Präzisierung der logischen Reihenfolge!
Zwei Möglichkeiten:
a) Für große n soll |an-a| klein werden
b) Für eine bestimmte Fehlergrenze soll es ein
Folgeglied geben, ab dem |an-a| kleiner ist.
Man verwendet b) für die Grenzwertdefinition – und zwar
Für beliebige „Fehlergrenzen“:
∀ ∃ ∀ | a − an |< ε
ε >0 Nε n > Nε
Oliver Passon
Folgen, Reihen, Grenzwert
7
Definition: Nullfolge bei a=0:
∀ ∃ ∀ | an |< ε
ε >0 Nε n > Nε
(an) konvergiert gegen a ↔ (an-a) ist Nullfolge
Satz: 1/n ist Nullfolge
Beweis: für jedes ε>0 gibt es m: 1/m<ε. Setzte Nε=m
Oliver Passon
Folgen, Reihen, Grenzwert
8
an = n k ⋅ q n mit : k = 10, q = 0,8
a1 = 0,8
a2 = 655,36
a3 = 30233,088
M
Diese Folge ist tatsächlich eine
Nullfolge! „Grund“: qn mit |q|<1
ist Nullfolge („geometrische Folge“)
Oliver Passon
Folgen, Reihen, Grenzwert
9
Definition:
lim a
n →∞
n
=a
bedeutet:
• Folge ist konvergent
• Grenzwert ist a
• ∞ ist nur ein Symbol und keine Zahl
• alle anderen Folgen heißen divergent
Oliver Passon
Folgen, Reihen, Grenzwert
10
Zusammenhang zwischen weiteren Begriffen:
Eine Folge heißt:
• monoton fallend (steigend): an+1≤an (an+1≥an)
• beschränkt: es gibt M, sodass für alle n: |an|<M
• Es gilt: jede konvergente Folge ist beschränkt!
• Satz: jede beschränkte monotone Folge
konvergiert
• Aber: beschränkte nicht monotone Folgen
konvergieren nicht: Bsp. (-1)n
Oliver Passon
Folgen, Reihen, Grenzwert
11
• Definition: a Häufungswert (HW) von (an)
gdw. eine Teilfolge von (an) gegen a
konvergiert.
• Satz (Bolzano-Weierstraß): Jede
beschränkte reelle Folge besitzt
mindestens einen Häufungswert.
• Bsp. (-1)n hat HW 1 und -1!
Oliver Passon
Folgen, Reihen, Grenzwert
12
Strategien für den Nachweis der Konvergenz:
• Explizite Konstruktion von Nε
• Einschließungssatz: gilt an≤ bn ≤ cn und an
cn konvergieren gegen g, dann auch bn
• Beschränktheit und Monotonie
nachweisen
• Cauchy-Kriterium („jede Cauchy-Folge
konvergiert“)
Oliver Passon
Folgen, Reihen, Grenzwert
13
Hauptsatz über konvergente Folgen
(„Grenzwertsatz“)
an und bn seien konvergente Folgen mit Grenzwerten
a und b. Die Zahlen λ und µ ε R. Es gilt:
lim(λan + µbn ) = λa + µb
n →∞
lim(an ⋅ bn ) = a ⋅ b
n →∞
a
lim(an / bn ) =
n →∞
b
Oliver Passon
Folgen, Reihen, Grenzwert
14
Funktionengrenzwerte
Klar: In der Analysis untersuchen wir in der Regel
Grenzwertprozesse von Funktionen – und nicht von Folgen!
lim f ( x) = A :⇔
x→a
∀
( xn ):lim xn = a
lim f ( xn ) = A
n →∞
Nebenbemerkung: a muss „Häufungspunkt“ sein…
Oliver Passon
Folgen, Reihen, Grenzwert
15
(unendliche) Reihen
Für jeder Folge an kein eine
„Partialsummenfolge“ sn definiert
werden:
sn = a1 + a2 + L + an
∑
∞
r =0
a r = ( s n ) n εN
Achtung: Hier steht nicht das Ergebnis einer
„unendlichen“ Summation, sondern eine Folge!
Oliver Passon
Folgen, Reihen, Grenzwert
16
Falls die Partialsummenfolge konvergiert kann man
schreiben:
n
S = ∑r =0 ak = lim sn = lim ∑ ar
∞
n →∞
n →∞
r =0
Reihen sind also spezielle Folgen, sodass sie vom rein
logischen Standpunkt aus nicht betrachtet werden
müssten. Es ist aber nützlich…
Zudem folgt aus ihrer speziellen Bauart, dass besonders
übersichtliche Konvergenzkriterien gelten…
Oliver Passon
Folgen, Reihen, Grenzwert
17
Zusammenhang zwischen Folgen und Reihen
∞
∑a
i
= S ⇒ lim ai = 0
Die Umkehrung gilt bekanntlich nicht:
Diese Reihe divergiert!
(„harmonische Reihe“)
∞
∑
1
n
∞
1
q =
∑
1− q
n =0
falls | q |< 1
n
Jedoch gilt:
(„geometrische Reihe“)
Oliver Passon
Folgen, Reihen, Grenzwert
18
∞
Bsp.:
1+ + +L = ∑ (
1
2
1
4
n =0
)
1 n
2
1
=
=2
1
1− 2
Beide Bögen sind gleich lang!
Oliver Passon
Folgen, Reihen, Grenzwert
19
Auf beiden Kreisbögen bewegen sich nun zwei „Käfer“ mit der selben
Geschwindigkeit.
Beide erreichen ihr Ziel gleichzeitig (Punkt 2 bzw. Punkt 2/3)
Einer hat sein Ziel zuvor unendlich oft umrundet!
Oliver Passon
Folgen, Reihen, Grenzwert
20
Paradoxien des Grenzwertbegriffs
und
Zusammenfassung
• Der Grenzwertbegriff formalisiert, das bestimmte
Prozesse endlich sind, obwohl sie nicht in
endlich vielen Denkschritten durchlaufen werden
können…
• Intuitiv möchte man mit dem „unendlich kleinen“
argumentieren
• Die Grenzwertdefinition spricht stattdessen nur
von endlich kleinen Objekten – jedoch beliebig
kleinen Objekten!
Oliver Passon
Folgen, Reihen, Grenzwert
21