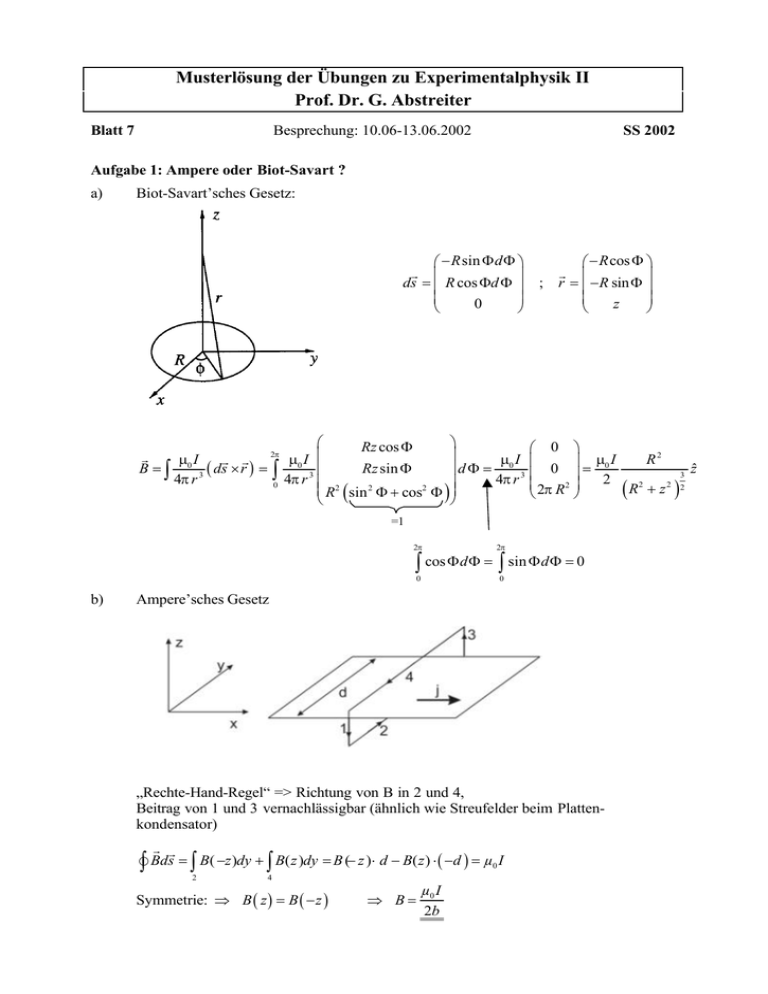
∫ ∫ ∫ ∫ ∫ ∫ ∫

Musterlösung der Übungen zu Experimentalphysik II
Prof. Dr. G. Abstreiter
Blatt 7
Besprechung: 10.06-13.06.2002
SS 2002
Aufgabe 1: Ampere oder Biot-Savart ?
a)
Biot-Savart’sches Gesetz:
 − R sin Φ d Φ 
 − R cos Φ 
r 
r 


ds =  R cos Φd Φ  ; r =  −R sin Φ 




0
z






Rz cos Φ
 0 
2π


r
µ0 I
r r
µ0 I
µ0 I 
R2
 = µ0 I
B =∫
ds
×
r
=
Rz
sin
Φ
d
Φ
=
0
zˆ
(
)


3 
3
∫0 4π r 3 
 2
4π r 3
4
π
r

2
2
2


2
 R2 (sin 2 Φ + cos2 Φ )
(R + z )
 2π R 


=1
2π
2π
0
0
∫ cos Φ d Φ =
b)
∫ sin Φ d Φ = 0
Ampere’sches Gesetz
„Rechte-Hand-Regel“ => Richtung von B in 2 und 4,
Beitrag von 1 und 3 vernachlässigbar (ähnlich wie Streufelder beim Plattenkondensator)
r r
Bds
Ñ∫ = ∫ B( −z )dy + ∫ B( z )dy = B (− z )⋅ d − B(z ) ⋅ ( −d ) = µ0 I
2
4
Symmetrie: ⇒ B ( z ) = B ( − z )
⇒ B=
µ0 I
2b
c)
Ampere’sches Gesetz:
v v
Bds
Ñ∫ = µ 0 I , mit I dem eingeschlossenen Strom
I
π ( r1 + d ) 2 − π r12
I
Stromdichte im äußeren Rohr: j = −
π ( r2 + d ) 2 − π r22
0 ≤ r ≤ r1 :
2π rB = 0 ⇒
B= 0
Stromdichte im inneren Rohr: j =
I
⋅ (π r 2 − π r12 )
2
2
π ( r1 + d ) − π r1
r1 ≤ r ≤ r1 + d :
2π rB = µ 0
r1 + d ≤ r ≤ r2 :
B=
r2 ≤ r ≤ r2 + d :
2π rB = µ 0 I −
r2 + d ≤ r < ∞ :
⇒ B=
µ0 I ( r 2 − r12 )
2π r (( r1 + d )2 − r12 )
µ0 I
2π r
2π rB = 0
µ0 I
⋅ (π r 2 − π r22 )
π (r2 + d ) 2 − π r22
⇒
⇒
B=
µ0 I 
( r 2 − r22 ) 
1
−


2π r  (r2 + d ) 2 − r22 
B =0
B
r
r
1
r +d
1
r
2
r +d
2
Aufgabe 2: Helmholtz Spulen
a) In Aufgabe 1 a) wurde B berechnet:
µ I
R2
B= 0
3
2
2
2 2
(R + z )
∂B µ 0 I
=
∂z
2
−3 zR 2
5
( R2 + z 2 ) 2
= −3B
∂2 B
=0
∂z 2
;
r2 = R 2 +z 2
z
r2
;
∂2 B
4z 2 − R2
=
3
B
∂z 2
r4
⇔
z=±
R
2
Aufgabe 3: Kraft zwischen zwei Elektronenstrahlen
a) Lorentzkraft:
µ0 I1
2π r
µI
FB = I 2 ∆l 2 ⋅ B 1 ( d ) = I 2 ∆l2 0 1
2π d
B1 ( r ) =
Für das Magnetfeld des Strahls 1 gilt (Vorlesung):
am Ort von Strahl 2 folgt damit:
FB µ0 I1 I 2
=
=
∆l
2π d
N
(10 mA) 2
2
N
A
= 1,0 ⋅10−9
2π ⋅ 0.02m
m
4π ⋅10 −7
Da die Ströme in gleiche Richtung fließen, wirkt die Lorentz-Kraft anziehend.
(„Rechte-Hand-Regel“ und „Drei-Finger-Regel“)
b) Energie der Elektronen:
1
me v2 = e ⋅ U B
2
⇒
v=
2eU B
me
dQ dQ dl
dQ
=
⋅ = λ ⋅ v mit der Linienladungsdichte λ =
dt
dl dt
dl
−31
me
I
9,110
⋅
kg
C
⇒ λ = =I⋅
= 10mA ⋅
= 3,08 ⋅ 10−10
−19
3
v
2eU B
2 ⋅1,6 ⋅10 As ⋅ 3 ⋅10 V
m
Strom: I =
λ1 = λ2 = λ
Coulombkraft:
Für das elektrische Feld des Strahls 1 gilt (Vorlesung): E1 ( r ) =
am Ort von Strahl 2 folgt damit:
1 λ1
2πε 0 r
FE = λ2 ∆ l 2 ⋅ E1 ( d ) = λ2 ∆l2
3,08 ⋅10 −10 ) Vm
(
FE
λ2
N
=
=
= 85,2 ⋅10 −8
−12
∆l 2πε 0 d 2π ⋅ 8,85 ⋅10 C ⋅ 0,02 m
m
λ1
2πε 0 r
2
Achtung: Bei der Herleitung wurden keine relativistischen Effekte (z.B. Geschwindigkeit
der Elektronen in Abhängigkeit von der Beschleunigungsspannung) berücksichtigt. Sie
gilt also zunächst nur für Geschwindigkeiten deutlich kleiner also c)
FE FB
I2
µ0 I 2
1
c)
=
⇔
=
⇔ v2 =
= c2
2
∆l ∆l
2πε 0 dv
2π d
ε 0 µ0
Die Elektronen müßten also Vakuumlichtgeschwindigkeit erreichen (das geht nicht!)
Die Coulombkraft ist also stets größer als die Lorentzkraft.
d) Die Lorentzkraft ist wie in a), die elektrostatische Ladung der Elektronen allerdings wird
die positive Hintergrundladung der Rumpfionen im Metalldraht kompensiert. Es wirkt
also keine Coulombkraft zwischen den Drähten.
F FB
=> Gesamtkraft:
=
∆l ∆l