Document

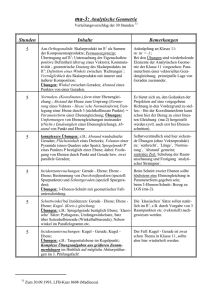
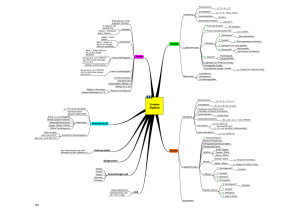
Lernkarten
Analytische Geometrie
6 Seiten
Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt
wenden, nochmals einlegen und die Rückseite drucken.
Am besten druckt man die Karten auf festem Papier oder auf VisitenkartenPapier, so dass man sie hinterher zerschneiden kann.
Da dies eine Erstproduktion ist, bitte ich, mir eventuelle Fehler mitzuteilen
sowie Verbesserungs- und Ergänzungsvorschläge zu machen.
Jens Möller.
Wie berechnet man den Winkel
zwischen zwei Geraden ?
Wie bestimmt man die Länge

eines Vektors a ?
Wie berechnet man den Winkel
zwischen zwei Ebenen ?
Wie berechnet man den Winkel zwischen
einer Gerade und einer Ebene ?
Wann sind zwei Vektoren parallel ?
Wann sind zwei Vektoren orthogonal ?
Wie bestimmt man den Abstand zweier
Punkte A und B ?
Wie lauten die Gleichungen der
Koordinatenebnen ?
Wie lautet die Ebenengleichung in
Achsenabschnittsform ?
Wozu benötigt man sie ?
Wie lauten die Gleichungen der Ebenen, die
parallel zu den Koordinatenebnen sind ?

| a |=
 
| a ⋅b |
cos α =  
| a |⋅|b |
a12 + a22 + a32
 
| a ⋅n |
sin α =  
| a |⋅| n |
 
| n1 ⋅ n2 |
cos α = 

| n1 | ⋅ | n2 |
 
 
a ⊥ b ⇔ a ⋅b =
0

 

a  b ⇔ a =⋅
k b
mit k ≠ 0
Die Vektoren sind linear abhängig.
x1 x2 Ebene ⇒ x3 =
0
AB =
(a1 − b1 )2 + (a2 − b2 )2 + (a3 − b3 )2
x1 x3 Ebene ⇒ x2 =
0
x2 x3 Ebene ⇒ x1 =
0
=
x3 c ⇒
parallel zur x1 x2 Ebene
=
x2 b ⇒
parallel zur x1 x3 Ebene
=
x1 a ⇒
parallel zur x2 x3 Ebene
oder
AB =
(∆x1 )2 + (∆x2 )2 + (∆x3 )2
x
x1
x
+ 2 + 3 =
1
a
b
c
benötigt man zur Bestimmung der
Spurpunkte und zum Zeichnen.
Wie lautet die Ebenengleichung in
Koordinatenform ?
Welche Bedeutung hat die Größe von D?
Wie lautet die Ebenengleichung in
Parameterform?
Welche Vektoren darf man kürzen?
Wie erhält man aus der Koordinatenform
einen Vektor, der orthogonal zur Ebene ist.
Wie erhält man einen Vektor, der auf
zwei anderen Vektoren senkrecht steht?
Wie lautet die Normalform der
Ebenengleichung?
Wie kommt man von der Normalform zur
Koordinatenform?
Wie lautet die Hesse-Normel-Form der
Ebenengleichung?
Wie lautet die Formel für den Abstand eines
Punktes P von einer Ebene E?
Wie berechnet man die Mitte einer Strecke?
Wie lautet die Formel für den Abstand einer
Ebene E zum Ursprung?
 




x = x0 + s ⋅ ( x0 − x1 ) + t ⋅ ( x0 − x2 )


 
 
a
b



x0 Stützvektor
=
a und b Richtungsvektoren
A ⋅ x1 + B ⋅ x2 + C ⋅ x3 + D =
0
für D = 0 geht die Ebene durch den
Ursprung.
Nur die Richtungsvektoren darf man kürzen.
A ⋅ x1 + B ⋅ x2 + C ⋅ x3 + D =
0
Durch das Kreuzprodukt
 A
  
⇒ n=
B
C 
 

 
n= a × b
 x1 
  A
  
     
[ x − x0 ] ⋅ n = 0 ⇔  x2  − x0  ⋅  B = 0
 x3 
  C 
⇒ A ⋅ x1 + B ⋅ x2 + C ⋅ x3 + D =
0
d=



[ x − x0 ] ⋅ n =0
   
⇔ n ⋅ x =n ⋅ x0 =− D
A ⋅ p1 + B ⋅ p2 + C ⋅ p3 + D
A ⋅ x1 + B ⋅ x2 + C ⋅ x3 + D
A +B +C
A2 + B 2 + C 2
2
d=
2
2
D
A +B +C
2
2
2
=0
 a + b1 a2 + b2 a3 + b3 
M 1
|
|

2
2
2


Was versteht man unter Spurpunkten einer
Ebene und wie bestimmt man sie?
Was versteht man unter Spurpunkten einer
Gerade und wie bestimmt man sie?
Wie lautet die Geradengleichung in
Parameterform ?
Wie fällt man das Lot auf eine Ebene?
Wie spiegelt man einen Punkt an einer Ebene?
Wie erhält man die Spurgeraden einer Ebene?
Wie lauten die Gleichungen der
Koordinatenachsen?
Wie kann man den Abstand zweier
windschiefer Geraden bestimmen?
Wie bestimmt man den Abstand eines
Punktes P zu einer Geraden g?
Wie bestimmt man den Betrag eines Vektors?
Spurpunkte = Schnittpunkte einer Geraden mit
den Koordinatenebenen.
Setze in der Geradengleichung jeweils
=
x1 0=
oder x2 0=
oder x3 0 .
Spurpunkte = Schnittpunkte einer Ebene mit den
Koordinatenachsen.
x
x1
x
+ 2 + 3 =1 →
a
b
c
So erhält man jeweils einen Spurpunkt.
S 1 (a / 0 / 0) , S 2 (0 / b / 0) und S 3 (0 / 0 / c)
Lot auf eine Ebene:
 

Lot : x = xP + t ⋅ n
 


g : x = x0 + t ⋅ ( x0 − x1 )

 
a

Der Richtungsvektor a darf gekürzt werden.
Die Lotgerade mit der Ebene schneiden,
den Parameter verdoppeln und in die
Lotgerade einsetzen.

g: x =

h : x=
Die Ebene E wird mit den Koordinatenebenen
=
x1 0=
oder x2 0=
oder x3 0
geschnitten.


x0 + s ⋅ a
  

⇒ n=
a×b

xP + t ⋅ b
  
Hilfsebene : [ x − x0 ] ⋅ n =
0
x1 − Achse : ⇒
1

x=
t ⋅0
 
 0
H : A x1 + B x2 + C x3 + D =
0
x2 − Achse : ⇒
 0

x=
t ⋅1
 
 0
x3 − Achse : ⇒
 0

x=
t ⋅ 0
 
1
Abst. von P zu H =

a =
A ⋅ p1 + B ⋅ p2 + C ⋅ p3 + D
A2 + B 2 + C 2
Man stellt eine Hilfsebene H auf, die durch P
geht und g senkrecht schneidet.
a12 + a2 2 + a32
H ∩ g= F
⇒ d= PF
Wie normiert man einen Vektor
auf die Länge 1 ?
Wie schneidet man eine Gerade
mit einer Ebene?
Wie bestimmt man den
Schnittpunkt zweier Geraden?
Wie bestimmt man die Schnittgerade
zweier Ebenen, die in Koordinatenform
gegeben sind?
Wie bestimmt man die Schnittgerade
zweier Ebenen, wenn die eine in
Koordinatenform und die andere in
Parameterform gegeben ist?
Woran erkennt man, dass zwei Geraden
windschief sind?
Woran erkennt man, dass zwei Geraden
parallel sind?
Woran erkennt man, dass zwei Geraden
identisch sind?
Wie bestimmt man den Schwerpunkt eines
Dreiecks ABC?
Wie erkennt man, dass drei Vektoren



a , b und c
linear abhängig sind?
g komponentenweise einsetzen in
E (in Koordinatenform)
⇒ tS
Man teilt den Vektor durch seine Länge
1 

=
a0
 ⋅a
|a|
Der normierte Vektor hat die Länge 1.
tS in g einsetzen ⇒ S
1.Mögl.:
Je zwei entsprechende Spurgeraden schneiden
⇒ S1 und
S2
⇒ g
System mit 3 Gleichungen und 2 Unbekannten
aus 2 Zeilen berechne s und t
2.Mögl.:
  
a=
n 1 × n2 und ein SP ⇒ g
3. Mögl.:
setze z.B. x1 =
t... ⇒ x2 und
g 1 und g 2 komponentenweise gleichsetzen ⇒
für die 3. Zeile mache die Kontrolle:
falls kein Widerspruch
x3
⇒
S
⇒ g
windschief:


a ≠ k ⋅ b , d.h. verschiedene Richtungen
und kein Schnittpunkt
E 1 (Parameterform) einsetzen in E 2 (Koordinatenform)
⇒ s = a ⋅t + b ⇒
⇒
einsetzen in E 1
g in Parameterform
identisch:


a= k ⋅ b , d.h. gleiche Richtung
parallel:


a= k ⋅ b ,d.h. gleiche Richtung
und P1/ 2 liegt auf g 2 /1 (Punktprobe)
und P 1 , 2 liegt nicht auf g 2 , 1 (Punktprobe)
Einer der Vektoren lässt sich als Linearkombination der beiden anderen schreiben



z.B. a = s ⋅ b + t ⋅ c
 a +b +c a +b +c a +b +c 
S 1 1 1| 2 2 2| 3 3 3
3
3
3


Wie bestimmt man den Flächeninhalt eines
Rechtecks?
Wie bestimmt man den Flächeninhalt eines
Parallelogramms?
Wie bestimmt man den Flächeninhalt einer
Raute (= Rhombus)?
Wie bestimmt man den Flächeninhalt eines
Dreiecks?
Wie bestimmt man den Flächeninhalt eines
Trapezes?
Wie lautet der Satz des Pythagoras?
Wie berechnet man die Länge der Diagonale in
einem Quadrat?
Wie berechnet man die Länge der Diagonale in
einem Rechteck?
Wie berechnet man ein Spatvolumen?
Wie berechnet man den Umfang
eines Kreises?
A = g ⋅ h oder A = a ⋅ b ⋅ sin γ
oder
 
A= | a × b |
A=
1
2
g ⋅ h oder A= a ⋅ b ⋅ sin γ
oder
 
A =12 ⋅ | a × b |
1
2
a2 + b2 =
c2
=
c
a2 + b2
U=
π ⋅ d oder U =
2π ⋅ r
A=
Länge ⋅ Breite =
a ⋅b
e⋅ f
2
e, f = Diagonalen,
die stehen senkrecht aufeinander
und halbieren sich.
A=
ATrapez =
=
d
a+c
⋅h
2
2 ⋅a
Ein Spatvolumen wird von drei linear unab −
 

hängigen Vektoren a , b und c aufgespannt :
  
VSPAT = | (a × b ) ⋅ c |
Wie berechnet man die Fläche eines Kreises?
Wie bestimmt man das Volumen einer
Pyramide?
Wie bestimmt man den Abstand
zweier paralleler Ebenen?
Wie bestimmt man den Abstand zweier
paralleler Geraden?
Wie spiegelt man einen Punkt P an einem
Punkt Q?
Wann sind die Ebenen
E1 und E2 orthogonal?
Wie erkennt man, dass die Ebene E und
die Gerade g orthogonal sind?
Wie erkennt man, dass die Ebene E und
die Gerade g parallel sind?
Wie bestimmt man das Volumen eines
Kegels?
Wie bestimmt man das Volumen eines
Zylinders?
VPyramide =
1
⋅ G ⋅ h oder
3
1   
⋅ | (a × b ) ⋅ c |
6
A= π ⋅ r ²
oder
1

 6 nur , wenn die Grundfl. ein Dreieck ist.
Man wählt einen Punkt P auf g1 und bestimmt
den Abstand des Punktes zur Geraden g 2 .
Dazu stellt man eine Hilfsebene durch P und
senkrecht zu g 2 auf.
H ∩ g2 = F
A=
π
4
⋅d²
Man wählt einen Punkt aus E1 und bestimmt
mit Hilfe der Formel (HNF) den Abstand des
Punktes zur Ebene E2 .
⇒ d = PF
  
x=
xQ + PQ
P
 
n1 ⋅ n2 =
0
 
n⋅a =
0
und
P∉E
V = G ⋅ h = π r² ⋅ h


n= k ⋅ a
V=
1
3
G ⋅ h=
1
3
π r² ⋅ h