Repetition MB2, LU9

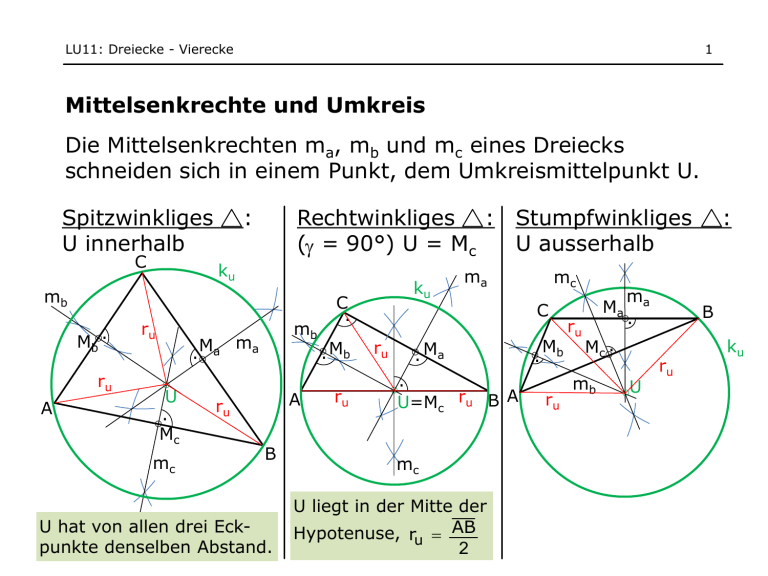
LU11: Dreiecke - Vierecke
1
Mittelsenkrechte und Umkreis
Die Mittelsenkrechten ma, mb und mc eines Dreiecks
schneiden sich in einem Punkt, dem Umkreismittelpunkt U.
Spitzwinkliges
U innerhalb
C
:
Rechtwinkliges : Stumpfwinkliges
( = 90°) U = Mc
U ausserhalb
ku
mb
Mb
.
ru
A
ru
. Ma
U
.
Mc
mc
mb
ma
A
ru
B
U hat von allen drei Eckpunkte denselben Abstand.
ku
C
.
. Mb
ru
ru
ma
. Ma
.
U=Mc ru B A
mc
U liegt in der Mitte der
Hypotenuse, ru  AB
2
mc
C
.
Mb
ru
ru
Ma
ma
.
Mc .
mb
U
:
B
ru
ku
LU11: Dreiecke - Vierecke
2
Winkelhalbierende und Inkreis
Die Winkelhalbierenden w , w und w eines Dreiecks
schneiden sich in einem Punkt, dem Inkreismittelpunkt I.
C
W
Y.
a
w ri
b
kI
c
w
I
w
A
W
• Der Inkreismittelpunkt liegt
immer im Innern eines
Dreiecks.
ri
.
Z
ri
W
.X
B
• Der Inkreismittelpunkt hat
von allen drei Seiten
denselben Abstand.
• Der Radius ri steht senkrecht
auf die Dreiecksseiten.
Der Berührpunkt ist i. A. nicht identisch mit dem Schnittpunkt
der Winkelhalbierenden mit der Dreiecksseite: z. B. Z ≠ W
LU11: Dreiecke - Vierecke
3
Seitenhalbierende und Schwerpunkt
Die Seitenhalbierenden sa, sb und sc eines Dreiecks
schneiden sich in einem Punkt, dem Schwerpunkt S.
C
• Der Schwerpunkt liegt immer
im Innern des Dreiecks.
Mb
sc
.
b
c
.
Mc
1
a
. Ma
S
sa
A
2
sb
B
• Eine Seitenhalbierende
(Schwerlinie) ist die Verbindungslinie von der Seitenmitte
zur gegenüberliegenden Ecke.
• Der Schwerpunkt teilt jede
Seitenhalbierende im
Verhältnis 2 : 1.
LU11: Dreiecke - Vierecke
4
Höhen und Höhenschnittpunkt
Die Höhen ha, hb und hc eines Dreiecks schneiden sich in
einem Punkt, dem Höhenschnittpunkt H.
Spitzwinkliges
H innerhalb
:
C
b
A
H
hc
.
Hc
:
H
. Ha
ha
Hb .
Rechtwinkliges : Stumpfwinkliges
( = 90°) H = C
H ausserhalb
b
a
hb
ha
A
C=H
.
hb
hc
.
c
.
a
.
B
c
B
Die Höhe ist die Senkrechte
von einer Ecke zur gegenüberliegenden Seite.
a
C
ha b
hb
hc
.
B
c
A
Der Höhenschnittpunkt
liegt in der Ecke mit
dem rechten Winkel.
Zwei Seiten müssen
verlängert werden.
LU11: Dreiecke - Vierecke
5
Konstruktionsaufgaben
Zu einer Konstruktionsaufgabe gehören:
a) Überlegungsfigur b) Konstruktion c) Konstruktionsbericht
Beispiel: Konstruiere ein Dreieck aus: ha = 4,5 cm ; a = BC = 6 cm ;   48
Überlegungsfigur
Konstruktion
C
ÜF ergänzen
.
ha
g
A
.
Lösung grün
C
a

a
B .
► Ecken beschriften
► Gegebene Stücke
mit Farbe einzeichnen
und beschriften.
c
A
g
Konstruktionsbericht
1. Höhenstreifen für ha
 a, g
2. B auf a wählen
3. BC auf a abtragen C
4.  in B an a abtragen
c
5. c  g  A
B
Tipp: Ist eine Höhe gegeben,
beginne mit dem Höhenstreifen!
LU11: Dreiecke - Vierecke
5
Trapeze
Ein Viereck mit zwei parallelen Seiten heisst Trapez.
D
c
.
h
m
d
C
b
.
A
B
a
a, c
Grundseiten
Fläche
b, d
Schenkel
h
Höhe
A mh
 a  c h
2
m
Mittellinie
Es gibt…
… das allgemeine, das rechtwinklige und das gleichschenklige
Trapez.
D
D
C
.
C
D
C
.
A
B
A
B
A
B