Computational Chemistry SS07
Werbung

Slide 1
Inhalt der Vorlesung „Computational Chemistry“
Inhalt: Beschreibung von Molekülen mit computerbasierten Methoden
→ insbesondere Moleküleigenschaften:
Methoden
• Struktur: die Molekülgeometrie
welche Gestalt haben Moleküle ?
Kraftfelder bzw.
Molekülmechanik (MM)
Quantenmechanik (QM)
• Konformationsraum von Molekülen
Energieminimierung
welche Anordnungen der Atome sind sinnvoll ? Samplingmethoden
• zeitliche Bewegung von Molekülen
wie finden Konformationsänderungen statt?
Moleküldynamik (MD)
• Berechnung von Interaktionsenergien
Freie-Energie-Rechnungen
wie stark bindet ein Ligand an ein Protein?
1. Vorlesung SS12
Computational Chemistry
1
Slide 2
Was diese Vorlesung nicht behandelt
(1) Docking
(2) Drug Design
Spezielle Lehrveranstaltungen, zum Teil für
den Masterstudiengang
(3) Grundlagen aus der Chemie und physikalischen Chemie:
•
Okettregel
•
Stöchiometrie
•
Thermodynamik (Massenwirkungsgesetz, Hauptsätze der Thermodynamik)
(4) Grundlagen aus der Mathematik (Analysis):
• Ableitungen
•
Integrale
1. Vorlesung SS12
Computational Chemistry
2
Slide 3
Was ist Computational Chemistry?
Computational Chemistry:
Arbeitsgebiet an der Schnittstelle von
theoretischer Chemie,
Molecular Modeling und
struktureller Bioinformatik.
Haupteinsatzbereich von Computational Chemistry:
finde mittels numerischer Rechnungen
Antworten auf chemische Probleme.
→ Vorhersage von Moleküleigenschaften
1. Vorlesung SS12
Computational Chemistry
3
Slide 4
Geschichte der Computational Chemistry
Geschichte der Computational Chemistry:
entweder recht lang - wenn man ab der Entwicklung der Quantenmechanik in
den 1920er Jahren als Ursprung der theoretischen Chemie rechnet,
oder recht jung, da genaue Rechnungen an Molekülen mit vielen hundert
Atomen erst seit der Entwicklung moderner, leistungsstarker Computer in den
1980er Jahren möglich sind.
Computerchemie gehörte stets zu den
Wissenschaftsgebieten mit den größten
Anforderungen an Rechenleistung.
Ca. 2/3 aller wissenschaftlich genutzten
Rechenzeit wird für quantenchemische
Applikationen und Moleküldynamik
(MD)-Simulationen verwendet.
1. Vorlesung SS12
Erwin Schrödinger
Computational Chemistry
Michael J.S. Dewar
4
Slide 5
Molekülgeometrie
1 .5 4 Å = 1 5 4 p m
C
1 .0 9 Å
C
C
Bindungslängen oder
Bindungsabstände
H
H
H
H
1 0 9 .5 °
H
1 .3 4 Å
C
C
H
H
C
120°
Bindungswinkel
1 .1 0 Å
H
H
H-C-H tetraedrisch
H-C-H planar
H
180°
N
H
C
C
N
O
O
1. Vorlesung SS12
Computational Chemistry
Torsionswinkel oder
Diederwinkel
(dihedral angles)
5
Slide 6
Darstellung chemischer Strukturen (I)
Die Valenzelektronen der Atome werden paarweise zu
Bindungen gruppiert
H
.
.
.
.
H C..H
.
.
H
H
.
.
H
H
C
H
H
H
.
.
..
C .. C
.
.
.
.
H H
H
H
C
H
C
H
Diese Darstellung als Lewis-Strukturen gibt die kovalenten
Bindungen zwischen den Atomen in einem Molekül wieder
1. Vorlesung SS12
Computational Chemistry
6
Slide 7
Darstellung chemischer Strukturen (II)
Freie Elektronenpaare, die nicht an einer Bindung beteiligt sind,
(engl.: lone pairs) werden der Übersichtlichkeit halber oft nicht gezeigt
H
.
.
.
H ..N .
.
.
H
H
H
N
N
H
H
H
H
H
H
O
H
+
H
+
H
N
O
+
+
H
N
H
H
N
H
O
H
C
O
Hypervalente Atome kontra Oktettregel
O
O
S
O
O
O
O
P
O
O
Identische Bindungslängen trotz
unterschiedlicher Darstellung !
→ mesomere Grenzstrukturen
Welche Bedeutung haben freie Elektronenpaare für Wasserstoffbrückenbindungen?
1. Vorlesung SS12
Computational Chemistry
7
Slide 8
Darstellung chemischer Strukturen (III)
Auch Kohlenstoffatome werden häufig weggelassen
→ die Ecken des Molekülgraphs
H
H
H
C
H
C
H
H
C
C
H
H
H
H
H
C
C
C
C
H
C
C
H
H
H
H
H
C
C
H
H
C
H H
H
C
C
H
H
C
H
H
Ecken und die Enden der Kanten stellen Kohlenstoffatome dar, die
jeweils mit der entsprechenden Anzahl an Wasserstoffatomen
abgesättigt werden.
1. Vorlesung SS12
Computational Chemistry
8
Slide 9
Darstellung chemischer Strukturen (IV)
Stereochemie
H
Keile markieren Bindungen zu Atomen,
die aus der Ebene hervortreten;
gestrichelte Keile solche, die nach
hinten zeigen
F
C
H3C
Cl
Vier verschiedene Substituenten an einem Kohlenstoffatom
bewirken Chiralität
H
F
C
H3C
1. Vorlesung SS12
H
F
C
Cl
Cl
Computational Chemistry
C H3
9
Slide 10
Zum Anfassen
Molekülbaukästen
Käuflich in verschiedenen Preisklassen erhältlich
1. Vorlesung SS12
Computational Chemistry
10
Slide 11
Nützliche Software
Visualisierung des Outputs verschiedenster
MM, MD und
QM-Programme
vmd
http://www.ks.uiuc.edu/Research/vmd/
Visualisierung und Kraftfeld
Ball
http://www.bioinf.uni-sb.de/OK/BALL
1. Vorlesung SS12
Computational Chemistry
11
Slide 12
Erhebung der Computational Chemistry „in den Adelsstand“
Der Ritterschlag für das Gebiet der Computational Chemistry war
gewissermaßen der Nobelpreis für Chemie in 1998 an
-
John Pople "for his development of
computational methods in quantum chemistry"
-
Walther Kohn "for his development
of the density-functional theory"
Diese Preise wurden in der Wissenschaftsgemeinde (“community”) mit ungeheurer
Befriedigung aufgenommen, nicht allein als Auszeichnung der beiden Forscher,
sondern als Auszeichnung des gesamten Gebiets.
1. Vorlesung SS12
Computational Chemistry
12
Slide 13
Isomere von C6H6
P ris m a n
Dewar
B e n zo l
B e n zo l
Dies sind einige der 217 denkbaren Graphen von C6H6, die mit der Oktettregel
vereinbar sind. Welche sind stabil ? Welches Molekül ist das stabilste ?
1. Vorlesung SS12
Computational Chemistry
13
Slide 14
Häufig verwendete Methoden
ab initio
Vollständig empirisch
Quantenmechanik
Molekülmechanik
Neuronale
Netze
Kraftfelder
semiempirische
MO-Methoden
Dichtefunktionaltheorie
coupled
cluster
zunehmender Rechenaufwand
machbare Größe des Molekülsystems
Anzahl Atome
1.000.000
200
50
10
Zunehmende Spezialisierung
auf bestimmte Eigenschaften
1. Vorlesung SS12
Computational Chemistry
14
Slide 15
Welche Methoden verwendet Computational Chemistry?
-
Molekül-Mechanik (empirische Kraftfelder AMBER, OPLS, CHARMM, GROMOS, ...)
-
Moleküldynamik (klassische Newton-Mechanik)
-
Semi-empirische Molekül-Orbital-Theorie (MNDO, AM1, PM3, OM2, MNDO/d, …)
-
Dichtefunktionaltheorie (LDA, B3LYP, …)
-
ab Initio Molekül-Orbital-Theorie (Hartree-Fock, Møller-Plesset, Coupled Cluster …)
zur Computational Chemistry gehören ebenfalls:
-
Quantitative Structure-Activity Relationships (QSAR)
-
Chemoinformatik
-
Docking
-
Graphische Darstellung von Strukturen und Eigenschaften
1. Vorlesung SS12
Computational Chemistry
15
Slide 16
Wozu brauchen Bioinformatiker Computational Chemistry?
Protein-Liganden Bindung
Protein-Protein Bindung
Proteinfaltung
Docking (Konformationsanalyse)
QSAR
...
/
http://www.aventis.com
Entwicklung von Medikamenten
http://www.dell.com
Univ. Buffalo cluster
1. Vorlesung SS12
Computational Chemistry
16
Slide 17
Überblick über den Inhalt der Vorlesung
Molekül-Mechanik
Quantenchemie
1
Einleitung
7
Molekülorbital Theorie
2
Strukturen, molekulare Kräfte
8
Semiempirische Molekül Orbital
3
Kraftfelder und Minimierung
4
Statistische Mechanik
9
5
Moleküldynamik-Simulationen
10 Chemische Reaktionen
6
Sampling des Konformationsraums
11 Berechnung von
Theorie
Solvatationsmodelle
Moleküleigenschaften
12 Intermolekulare Bindungen,
Berechnung von Bindungsenergien
13
Proteinfaltungssimulationen +
Zusammenfassung
Klausur 16. Juli 2012
10-12 Uhr
Slide 18
Schein
Es wird jede Woche in der Vorlesung 1 Übungsblatt ausgegeben, also insgesamt
etwa 10 – 11 Übungsblätter.
Jeder aktive Teilnehmer der Vorlesung muss ein eigenes Lösungsblatt abgeben.
An der Abschlussklausur kann teilnehmen, wer 50% der Punkte in den
Übungsblättern erreicht hat.
Einen Übungsschein über die erfolgreiche Teilnahme an der Vorlesung (6 LP)
gibt es bei erfolgreicher Teilnahme an der Abschlussklausur und/oder der
Nachklausur.
Die Note des Übungsscheins entspricht der besseren Note aus beiden Klausuren.
Sprechstunde: nach Vereinbarung (oder per e-mail)
1. Vorlesung SS12
Computational Chemistry
18
Slide 19
Übungsgruppen - Termine
Die Übungsgruppenleiterin ist
- Jennifer Metzger
[email protected]
Dienstags, 16:15 – 17:45 Uhr
oder wann haben Sie Zeit?
Wochentag / Uhrzeit
1. Vorlesung SS12
Computational Chemistry
19
Slide 20
Literatur - Quantenchemie
Kopien der Vorlesung kommen auf unsere Webseite
http://gepard.bioinformatik.uni-saarland.de
Introduction to Computational Chemistry
Frank Jensen, Wiley, €54 - 62
(im Semesterapparat)
Essentials of Computational Chemistry
Christopher J. Cramer, Wiley, €129-154
(im Semesterapparat)
1. Vorlesung SS12
Computational Chemistry
20
Slide 21
Literatur – Molekülmechanik/Simulationen
Molecular Modeling and Simulation
Tamar Schlick, Springer, € 64 – 72
(in Info-Bibliothek, Semesterapparat)
Molecular Modellng. Principles and Applications
2nd ed 2001, Andrew R. Leach,
Prentice Hall, €71 – 75
(in Semesterapparat
und Lehrbuchsammlung)
Computer Simulation of Liquids
M.P. Allen & D.J Tildesley, Oxford Science, €50 – 53
(im Semesterapparat)
1. Vorlesung SS12
Computational Chemistry
21
Slide 22
Aus VL „physikalische Chemie“ wird als bekannt
vorausgesetzt:
o
Thermodynamische Zustandsfunktionen (3.1)
o
Erster Hauptsatz der Thermodynamik (2/3)
o
Zweiter Hauptsatz der Thermodynamik (6)
o
innere Energie U, Entropie S, Enthalpie H,
freie Energie F, freie Enthalpie G
o
Grundlagen der Quantentheorie (13/14)
o
Schrödinger-Gleichung
o Aufbau
der Atome (15)
der Moleküle – Arten von Bindungen (kovalent, ionisch, H-Bindung),
Molekülorbitale (16)
o Aufbau
1. Vorlesung SS12
Computational Chemistry
22
Slide 23
Energiebegriff (I)
Was ist Energie, was ist Arbeit?
Mechanik: Kraft • Weg
Definition: Energie ist die Fähigkeit, Arbeit zu leisten.
Energie und Arbeit sind äquivalent.
Formen von Energie:
Lageenergie (mechanisch)
Elektrische Energie
Volumenarbeit
Chemische Energie
Welche Energieformen kennen Sie noch?
1. Vorlesung SS12
Computational Chemistry
23
Slide 24
Energiebegriff (II)
System: derjenige Teil der Welt, dem unser spezielles Interesse gilt.
Außerhalb des Systems befindet sich die Umgebung.
Offene Systeme erlauben den Austausch von Materie bzw. Wärme mit ihrer
Umgebung.
Abgeschlossene Systeme haben mit der Umgebung weder mechanischen
bzw. thermischen Kontakt.
Wenn wir an einem ansonsten isolierten System
Arbeit leisten, nimmt seine Fähigkeit, selbst Arbeit
zu leisten, zu, d.h. seine Energie nimmt zu.
Wenn das System Arbeit leistet, so nimmt
seine Energie ab.
1. Vorlesung SS12
Computational Chemistry
24
Slide 25
Der Erste Hauptsatz
„Dem System ist egal, in welcher Form Energie übertragen wird.“
Es funktioniert ähnlich wie ein Bankkonto in Bezug auf Geld.
Erster Hauptsatz: verändert sich ein System von einem Zustand in einen anderen
auf einem beliebigen adiabatischen Weg, so ist die geleistete Arbeit wad immer
dieselbe, unabhängig von der angewandten Methode.
Der Wert von wad ist für alle Wege gleich und hängt nur vom Anfangs- und
Endzustand ab.
wad = UE – UA
U ist die innere Energie des Systems.
U ist eine Zustandsfunktion.
1. Vorlesung SS12
Computational Chemistry
25
Slide 26
Newton‘sche Gesetze
2. Gesetz
Die Beschleunigung a ist dem Verhältnis von Kraft F
und Masse m proportional:
F m a
m x
2
m
d x
dt
3. Gesetz:
2
Actio = Reactio
Fg = m ∙ g
1. Vorlesung SS10
Computational Chemistry
26
Slide 27
Energie - Kraft
T : kinetische Energie eines Teilchens.
T x , y , z
1
1
in kartesischen Koordinaten:
U : potentielle Energie des Teilchens.
mv
2
2
2
2
2
m x y z
Meist hängt U nur von den Positionen ab, also U(x,y,z).
Die Newtonschen Bewegungsgleichungen lauten damit
Für die Kraft F gilt:
in einer Dimension
F U
in drei Dimensionen
(Nabla-)Operator
1. Vorlesung SS12
m xi
U
xi
xi x , y , z
U
F
mit dem Gradienten-
2
x
x
y
z
Computational Chemistry
27
Slide 28
Das mikrokanonische NVE-Ensemble
Gegeben: ein System mit Teilchenzahl N und Volumen V.
In einem idealisierten, von der Außenwelt abgeschlossenen, System ist die
Gesamtenergie E konstant = mikrokanonisches Ensemble
Bsp.: harmonischer Oszillator, Schwingungsbewegung in einem harmonischen
Potential
potentielle Energie U:
D: z.B. Federkonstante
U r
1
2
D r r0
U(r)
2
Wenn Gesamtenergie E0 gegeben,
r0
r
kinetische Energie = Gesamtenergie – pot. Energie
1. Vorlesung SS12
Computational Chemistry
28
Slide 29
Was kann man mit Computational Chemistry berechnen?
(1) Was ist die energetisch beste Konformation eines Moleküls?
Bewertung der Energie von Konformationen erfordert die Betrachtung, in welchen
Orbitalen des Moleküls seine Elektronen verteilt sind (Molekülorbitaltheorie).
(2) Einfluss des Lösungsmittels (Solvatationseffekte).
(3) Was sind bei Raumtemperatur erreichbare andere Konformationen
(Boltzmann)? Konformationssampling des Moleküls.
(4) Dynamik von Konformationsübergängen?
1. Vorlesung SS12
Computational Chemistry
29
Slide 30
Wie genau ist Computational Chemistry?
Durch Verwendung hochexakter Theorien wie der coupled-cluster-Methode können
für kleine Moleküle bis 10 Atome im Vakumm Eigenschaften genauer als im
Experiment berechnet werden!
Bei Unstimmigkeiten müssen mittlerweile oft die experimentellen Daten korrigiert
werden!
Für große Moleküle (Proteine) sind diese Verfahren jedoch nicht praktikabel.
Hier braucht man vereinfachte Verfahren wie Molekülmechanik (V2).
1. Vorlesung SS12
Computational Chemistry
30
Slide 31
Anwendungsbeispiel
Anwendung z.B.: Berechnung von Reaktivitäten und Lösungseigenschaften von
Aktiniden mittels relativistischer Quantenchemie am Pacific Northwest National
Laboratory.
„There are 177 underground waste storage tanks at Hanford. The tanks contain
wastes collected over almost 50 years of plutonium production. The wastes include
radioactive isotopes, toxic chemicals, corrosive liquids, organic solvents, and other
dangerous and hazardous substances.“
http://www.pnl.gov/tws/
Problem hier: es fehlen experimentelle Daten,
beispielsweise für die Löslichkeiten von
Uran-Verbindungen wie UF6 Computational Chemistry!
1. Vorlesung SS12
Computational Chemistry
31
Slide 32
Zusammenfassung
Computerchemie besitzt eine lange Geschichte.
Bedeutung der Computerchemie wuchs stets parallel zur Entwicklung der
Rechner.
Zwei wesentliche “Welten”: Quantenchemie Molekülmechanik
Quantenchemie für sehr kleine Moleküle ist heutzutage hoch exakt,
oft genauer als das Experiment
bei großen Systemen (z.B. Proteinen) müssen jedoch starke Näherungen
gemacht werden
Das wesentliche Lernziel dieser Vorlesung ist zu verstehen,
was die verschiedenen Methode leisten können und wo die Probleme liegen.
Für die Praxis: Welche Methode ist für welchen Zweck geeignet.
1. Vorlesung SS12
Computational Chemistry
32
Inhalt der Vorlesung „Computational Chemistry“
Inhalt: Beschreibung von Molekülen mit computerbasierten Methoden
→ insbesondere Moleküleigenschaften:
Methoden
• Struktur: die Molekülgeometrie
welche Gestalt haben Moleküle ?
Kraftfelder bzw.
Molekülmechanik (MM)
Quantenmechanik (QM)
• Konformationsraum von Molekülen
Energieminimierung
welche Anordnungen der Atome sind sinnvoll ? Samplingmethoden
• zeitliche Bewegung von Molekülen
wie finden Konformationsänderungen statt?
Moleküldynamik (MD)
• Berechnung von Interaktionsenergien
Freie-Energie-Rechnungen
wie stark bindet ein Ligand an ein Protein?
1. Vorlesung SS12
Computational Chemistry
1
Slide 2
Was diese Vorlesung nicht behandelt
(1) Docking
(2) Drug Design
Spezielle Lehrveranstaltungen, zum Teil für
den Masterstudiengang
(3) Grundlagen aus der Chemie und physikalischen Chemie:
•
Okettregel
•
Stöchiometrie
•
Thermodynamik (Massenwirkungsgesetz, Hauptsätze der Thermodynamik)
(4) Grundlagen aus der Mathematik (Analysis):
• Ableitungen
•
Integrale
1. Vorlesung SS12
Computational Chemistry
2
Slide 3
Was ist Computational Chemistry?
Computational Chemistry:
Arbeitsgebiet an der Schnittstelle von
theoretischer Chemie,
Molecular Modeling und
struktureller Bioinformatik.
Haupteinsatzbereich von Computational Chemistry:
finde mittels numerischer Rechnungen
Antworten auf chemische Probleme.
→ Vorhersage von Moleküleigenschaften
1. Vorlesung SS12
Computational Chemistry
3
Slide 4
Geschichte der Computational Chemistry
Geschichte der Computational Chemistry:
entweder recht lang - wenn man ab der Entwicklung der Quantenmechanik in
den 1920er Jahren als Ursprung der theoretischen Chemie rechnet,
oder recht jung, da genaue Rechnungen an Molekülen mit vielen hundert
Atomen erst seit der Entwicklung moderner, leistungsstarker Computer in den
1980er Jahren möglich sind.
Computerchemie gehörte stets zu den
Wissenschaftsgebieten mit den größten
Anforderungen an Rechenleistung.
Ca. 2/3 aller wissenschaftlich genutzten
Rechenzeit wird für quantenchemische
Applikationen und Moleküldynamik
(MD)-Simulationen verwendet.
1. Vorlesung SS12
Erwin Schrödinger
Computational Chemistry
Michael J.S. Dewar
4
Slide 5
Molekülgeometrie
1 .5 4 Å = 1 5 4 p m
C
1 .0 9 Å
C
C
Bindungslängen oder
Bindungsabstände
H
H
H
H
1 0 9 .5 °
H
1 .3 4 Å
C
C
H
H
C
120°
Bindungswinkel
1 .1 0 Å
H
H
H-C-H tetraedrisch
H-C-H planar
H
180°
N
H
C
C
N
O
O
1. Vorlesung SS12
Computational Chemistry
Torsionswinkel oder
Diederwinkel
(dihedral angles)
5
Slide 6
Darstellung chemischer Strukturen (I)
Die Valenzelektronen der Atome werden paarweise zu
Bindungen gruppiert
H
.
.
.
.
H C..H
.
.
H
H
.
.
H
H
C
H
H
H
.
.
..
C .. C
.
.
.
.
H H
H
H
C
H
C
H
Diese Darstellung als Lewis-Strukturen gibt die kovalenten
Bindungen zwischen den Atomen in einem Molekül wieder
1. Vorlesung SS12
Computational Chemistry
6
Slide 7
Darstellung chemischer Strukturen (II)
Freie Elektronenpaare, die nicht an einer Bindung beteiligt sind,
(engl.: lone pairs) werden der Übersichtlichkeit halber oft nicht gezeigt
H
.
.
.
H ..N .
.
.
H
H
H
N
N
H
H
H
H
H
H
O
H
+
H
+
H
N
O
+
+
H
N
H
H
N
H
O
H
C
O
Hypervalente Atome kontra Oktettregel
O
O
S
O
O
O
O
P
O
O
Identische Bindungslängen trotz
unterschiedlicher Darstellung !
→ mesomere Grenzstrukturen
Welche Bedeutung haben freie Elektronenpaare für Wasserstoffbrückenbindungen?
1. Vorlesung SS12
Computational Chemistry
7
Slide 8
Darstellung chemischer Strukturen (III)
Auch Kohlenstoffatome werden häufig weggelassen
→ die Ecken des Molekülgraphs
H
H
H
C
H
C
H
H
C
C
H
H
H
H
H
C
C
C
C
H
C
C
H
H
H
H
H
C
C
H
H
C
H H
H
C
C
H
H
C
H
H
Ecken und die Enden der Kanten stellen Kohlenstoffatome dar, die
jeweils mit der entsprechenden Anzahl an Wasserstoffatomen
abgesättigt werden.
1. Vorlesung SS12
Computational Chemistry
8
Slide 9
Darstellung chemischer Strukturen (IV)
Stereochemie
H
Keile markieren Bindungen zu Atomen,
die aus der Ebene hervortreten;
gestrichelte Keile solche, die nach
hinten zeigen
F
C
H3C
Cl
Vier verschiedene Substituenten an einem Kohlenstoffatom
bewirken Chiralität
H
F
C
H3C
1. Vorlesung SS12
H
F
C
Cl
Cl
Computational Chemistry
C H3
9
Slide 10
Zum Anfassen
Molekülbaukästen
Käuflich in verschiedenen Preisklassen erhältlich
1. Vorlesung SS12
Computational Chemistry
10
Slide 11
Nützliche Software
Visualisierung des Outputs verschiedenster
MM, MD und
QM-Programme
vmd
http://www.ks.uiuc.edu/Research/vmd/
Visualisierung und Kraftfeld
Ball
http://www.bioinf.uni-sb.de/OK/BALL
1. Vorlesung SS12
Computational Chemistry
11
Slide 12
Erhebung der Computational Chemistry „in den Adelsstand“
Der Ritterschlag für das Gebiet der Computational Chemistry war
gewissermaßen der Nobelpreis für Chemie in 1998 an
-
John Pople "for his development of
computational methods in quantum chemistry"
-
Walther Kohn "for his development
of the density-functional theory"
Diese Preise wurden in der Wissenschaftsgemeinde (“community”) mit ungeheurer
Befriedigung aufgenommen, nicht allein als Auszeichnung der beiden Forscher,
sondern als Auszeichnung des gesamten Gebiets.
1. Vorlesung SS12
Computational Chemistry
12
Slide 13
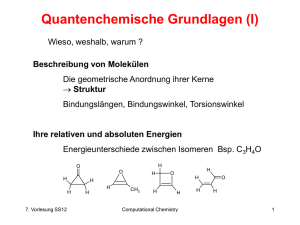
Isomere von C6H6
P ris m a n
Dewar
B e n zo l
B e n zo l
Dies sind einige der 217 denkbaren Graphen von C6H6, die mit der Oktettregel
vereinbar sind. Welche sind stabil ? Welches Molekül ist das stabilste ?
1. Vorlesung SS12
Computational Chemistry
13
Slide 14
Häufig verwendete Methoden
ab initio
Vollständig empirisch
Quantenmechanik
Molekülmechanik
Neuronale
Netze
Kraftfelder
semiempirische
MO-Methoden
Dichtefunktionaltheorie
coupled
cluster
zunehmender Rechenaufwand
machbare Größe des Molekülsystems
Anzahl Atome
1.000.000
200
50
10
Zunehmende Spezialisierung
auf bestimmte Eigenschaften
1. Vorlesung SS12
Computational Chemistry
14
Slide 15
Welche Methoden verwendet Computational Chemistry?
-
Molekül-Mechanik (empirische Kraftfelder AMBER, OPLS, CHARMM, GROMOS, ...)
-
Moleküldynamik (klassische Newton-Mechanik)
-
Semi-empirische Molekül-Orbital-Theorie (MNDO, AM1, PM3, OM2, MNDO/d, …)
-
Dichtefunktionaltheorie (LDA, B3LYP, …)
-
ab Initio Molekül-Orbital-Theorie (Hartree-Fock, Møller-Plesset, Coupled Cluster …)
zur Computational Chemistry gehören ebenfalls:
-
Quantitative Structure-Activity Relationships (QSAR)
-
Chemoinformatik
-
Docking
-
Graphische Darstellung von Strukturen und Eigenschaften
1. Vorlesung SS12
Computational Chemistry
15
Slide 16
Wozu brauchen Bioinformatiker Computational Chemistry?
Protein-Liganden Bindung
Protein-Protein Bindung
Proteinfaltung
Docking (Konformationsanalyse)
QSAR
...
/
http://www.aventis.com
Entwicklung von Medikamenten
http://www.dell.com
Univ. Buffalo cluster
1. Vorlesung SS12
Computational Chemistry
16
Slide 17
Überblick über den Inhalt der Vorlesung
Molekül-Mechanik
Quantenchemie
1
Einleitung
7
Molekülorbital Theorie
2
Strukturen, molekulare Kräfte
8
Semiempirische Molekül Orbital
3
Kraftfelder und Minimierung
4
Statistische Mechanik
9
5
Moleküldynamik-Simulationen
10 Chemische Reaktionen
6
Sampling des Konformationsraums
11 Berechnung von
Theorie
Solvatationsmodelle
Moleküleigenschaften
12 Intermolekulare Bindungen,
Berechnung von Bindungsenergien
13
Proteinfaltungssimulationen +
Zusammenfassung
Klausur 16. Juli 2012
10-12 Uhr
Slide 18
Schein
Es wird jede Woche in der Vorlesung 1 Übungsblatt ausgegeben, also insgesamt
etwa 10 – 11 Übungsblätter.
Jeder aktive Teilnehmer der Vorlesung muss ein eigenes Lösungsblatt abgeben.
An der Abschlussklausur kann teilnehmen, wer 50% der Punkte in den
Übungsblättern erreicht hat.
Einen Übungsschein über die erfolgreiche Teilnahme an der Vorlesung (6 LP)
gibt es bei erfolgreicher Teilnahme an der Abschlussklausur und/oder der
Nachklausur.
Die Note des Übungsscheins entspricht der besseren Note aus beiden Klausuren.
Sprechstunde: nach Vereinbarung (oder per e-mail)
1. Vorlesung SS12
Computational Chemistry
18
Slide 19
Übungsgruppen - Termine
Die Übungsgruppenleiterin ist
- Jennifer Metzger
[email protected]
Dienstags, 16:15 – 17:45 Uhr
oder wann haben Sie Zeit?
Wochentag / Uhrzeit
1. Vorlesung SS12
Computational Chemistry
19
Slide 20
Literatur - Quantenchemie
Kopien der Vorlesung kommen auf unsere Webseite
http://gepard.bioinformatik.uni-saarland.de
Introduction to Computational Chemistry
Frank Jensen, Wiley, €54 - 62
(im Semesterapparat)
Essentials of Computational Chemistry
Christopher J. Cramer, Wiley, €129-154
(im Semesterapparat)
1. Vorlesung SS12
Computational Chemistry
20
Slide 21
Literatur – Molekülmechanik/Simulationen
Molecular Modeling and Simulation
Tamar Schlick, Springer, € 64 – 72
(in Info-Bibliothek, Semesterapparat)
Molecular Modellng. Principles and Applications
2nd ed 2001, Andrew R. Leach,
Prentice Hall, €71 – 75
(in Semesterapparat
und Lehrbuchsammlung)
Computer Simulation of Liquids
M.P. Allen & D.J Tildesley, Oxford Science, €50 – 53
(im Semesterapparat)
1. Vorlesung SS12
Computational Chemistry
21
Slide 22
Aus VL „physikalische Chemie“ wird als bekannt
vorausgesetzt:
o
Thermodynamische Zustandsfunktionen (3.1)
o
Erster Hauptsatz der Thermodynamik (2/3)
o
Zweiter Hauptsatz der Thermodynamik (6)
o
innere Energie U, Entropie S, Enthalpie H,
freie Energie F, freie Enthalpie G
o
Grundlagen der Quantentheorie (13/14)
o
Schrödinger-Gleichung
o Aufbau
der Atome (15)
der Moleküle – Arten von Bindungen (kovalent, ionisch, H-Bindung),
Molekülorbitale (16)
o Aufbau
1. Vorlesung SS12
Computational Chemistry
22
Slide 23
Energiebegriff (I)
Was ist Energie, was ist Arbeit?
Mechanik: Kraft • Weg
Definition: Energie ist die Fähigkeit, Arbeit zu leisten.
Energie und Arbeit sind äquivalent.
Formen von Energie:
Lageenergie (mechanisch)
Elektrische Energie
Volumenarbeit
Chemische Energie
Welche Energieformen kennen Sie noch?
1. Vorlesung SS12
Computational Chemistry
23
Slide 24
Energiebegriff (II)
System: derjenige Teil der Welt, dem unser spezielles Interesse gilt.
Außerhalb des Systems befindet sich die Umgebung.
Offene Systeme erlauben den Austausch von Materie bzw. Wärme mit ihrer
Umgebung.
Abgeschlossene Systeme haben mit der Umgebung weder mechanischen
bzw. thermischen Kontakt.
Wenn wir an einem ansonsten isolierten System
Arbeit leisten, nimmt seine Fähigkeit, selbst Arbeit
zu leisten, zu, d.h. seine Energie nimmt zu.
Wenn das System Arbeit leistet, so nimmt
seine Energie ab.
1. Vorlesung SS12
Computational Chemistry
24
Slide 25
Der Erste Hauptsatz
„Dem System ist egal, in welcher Form Energie übertragen wird.“
Es funktioniert ähnlich wie ein Bankkonto in Bezug auf Geld.
Erster Hauptsatz: verändert sich ein System von einem Zustand in einen anderen
auf einem beliebigen adiabatischen Weg, so ist die geleistete Arbeit wad immer
dieselbe, unabhängig von der angewandten Methode.
Der Wert von wad ist für alle Wege gleich und hängt nur vom Anfangs- und
Endzustand ab.
wad = UE – UA
U ist die innere Energie des Systems.
U ist eine Zustandsfunktion.
1. Vorlesung SS12
Computational Chemistry
25
Slide 26
Newton‘sche Gesetze
2. Gesetz
Die Beschleunigung a ist dem Verhältnis von Kraft F
und Masse m proportional:
F m a
m x
2
m
d x
dt
3. Gesetz:
2
Actio = Reactio
Fg = m ∙ g
1. Vorlesung SS10
Computational Chemistry
26
Slide 27
Energie - Kraft
T : kinetische Energie eines Teilchens.
T x , y , z
1
1
in kartesischen Koordinaten:
U : potentielle Energie des Teilchens.
mv
2
2
2
2
2
m x y z
Meist hängt U nur von den Positionen ab, also U(x,y,z).
Die Newtonschen Bewegungsgleichungen lauten damit
Für die Kraft F gilt:
in einer Dimension
F U
in drei Dimensionen
(Nabla-)Operator
1. Vorlesung SS12
m xi
U
xi
xi x , y , z
U
F
mit dem Gradienten-
2
x
x
y
z
Computational Chemistry
27
Slide 28
Das mikrokanonische NVE-Ensemble
Gegeben: ein System mit Teilchenzahl N und Volumen V.
In einem idealisierten, von der Außenwelt abgeschlossenen, System ist die
Gesamtenergie E konstant = mikrokanonisches Ensemble
Bsp.: harmonischer Oszillator, Schwingungsbewegung in einem harmonischen
Potential
potentielle Energie U:
D: z.B. Federkonstante
U r
1
2
D r r0
U(r)
2
Wenn Gesamtenergie E0 gegeben,
r0
r
kinetische Energie = Gesamtenergie – pot. Energie
1. Vorlesung SS12
Computational Chemistry
28
Slide 29
Was kann man mit Computational Chemistry berechnen?
(1) Was ist die energetisch beste Konformation eines Moleküls?
Bewertung der Energie von Konformationen erfordert die Betrachtung, in welchen
Orbitalen des Moleküls seine Elektronen verteilt sind (Molekülorbitaltheorie).
(2) Einfluss des Lösungsmittels (Solvatationseffekte).
(3) Was sind bei Raumtemperatur erreichbare andere Konformationen
(Boltzmann)? Konformationssampling des Moleküls.
(4) Dynamik von Konformationsübergängen?
1. Vorlesung SS12
Computational Chemistry
29
Slide 30
Wie genau ist Computational Chemistry?
Durch Verwendung hochexakter Theorien wie der coupled-cluster-Methode können
für kleine Moleküle bis 10 Atome im Vakumm Eigenschaften genauer als im
Experiment berechnet werden!
Bei Unstimmigkeiten müssen mittlerweile oft die experimentellen Daten korrigiert
werden!
Für große Moleküle (Proteine) sind diese Verfahren jedoch nicht praktikabel.
Hier braucht man vereinfachte Verfahren wie Molekülmechanik (V2).
1. Vorlesung SS12
Computational Chemistry
30
Slide 31
Anwendungsbeispiel
Anwendung z.B.: Berechnung von Reaktivitäten und Lösungseigenschaften von
Aktiniden mittels relativistischer Quantenchemie am Pacific Northwest National
Laboratory.
„There are 177 underground waste storage tanks at Hanford. The tanks contain
wastes collected over almost 50 years of plutonium production. The wastes include
radioactive isotopes, toxic chemicals, corrosive liquids, organic solvents, and other
dangerous and hazardous substances.“
http://www.pnl.gov/tws/
Problem hier: es fehlen experimentelle Daten,
beispielsweise für die Löslichkeiten von
Uran-Verbindungen wie UF6 Computational Chemistry!
1. Vorlesung SS12
Computational Chemistry
31
Slide 32
Zusammenfassung
Computerchemie besitzt eine lange Geschichte.
Bedeutung der Computerchemie wuchs stets parallel zur Entwicklung der
Rechner.
Zwei wesentliche “Welten”: Quantenchemie Molekülmechanik
Quantenchemie für sehr kleine Moleküle ist heutzutage hoch exakt,
oft genauer als das Experiment
bei großen Systemen (z.B. Proteinen) müssen jedoch starke Näherungen
gemacht werden
Das wesentliche Lernziel dieser Vorlesung ist zu verstehen,
was die verschiedenen Methode leisten können und wo die Probleme liegen.
Für die Praxis: Welche Methode ist für welchen Zweck geeignet.
1. Vorlesung SS12
Computational Chemistry
32