Formale Sprachen und Automaten

Mengen
• Eine Menge ist eine Gruppe von Elementen, die
eine Einheit bilden (siehe z.B. Halmos 1976).
• Mengen können verschiedene Typen von Elementen
enthalten: Zahlen, Symbole, andere Mengen, etc.
Formale Sprachen
und
Automaten
• Mengen kann man dadurch charakterisieren, dass
man ihre Elemente aufzählt.
Menge1 = {1, 3, 4, 6}
Menge2 = {Moses, Josua, Ruth, Samuel}
• Die Elemente einer Menge haben nicht notwendigerweise etwas gemein.
Mathematisches Rüstzeug
Menge3 = {1, 4, Josua, Ruth}
• Reihenfolge und Dopplung der Elemente sind egal.
{1, 3, 4, 6} = {3, 6, 4, 1}
{1, 3, 4, 6} = {6, 6, 1, 3, 4, 6, 4}
– Typeset by FoilTEX –
1
– Typeset by FoilTEX –
2
Mengen 2
Mengen 3
• ∈ bezeichnet die Elementbeziehung, 6∈ die negierte
Form davon.
1 ∈ {1, 3, 4, 6}
5 6∈ {1, 3, 4, 6}
• A ist eine Teilmenge von B (A ⊆ B), genau dann,
wenn (gdw). für alle x gilt: wenn x ∈ A, dann
x ∈ B.
A = B gdw. A ⊆ B und B ⊆ A
• A ist eine echte Teilmenge von B (A ⊂ B), gdw.
A 6= B und A ⊆ B
• Es gibt eine Menge ohne Element: die leeren Menge.
Man schreibt { } oder ∅.
• Es gibt eine Menge, die alle Elemente enthält: die
universale Menge (manchmal als U geschrieben).
– Typeset by FoilTEX –
3
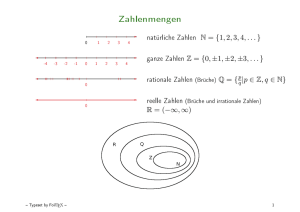
• Wenn Mengen sehr groß sind, ist es umständlich,
ihre Elemente aufzuzählen. Wenn Mengen unendlich
sind, ist dies praktisch sogar unmöglich.
• Man greift daher auf zwei alternative Darstellungen
zurück.
1. Entweder, man deutet mit . . . an, wie die Elementfolge fortgeführt werden könnte:
Menge der natürlichen Zahlen (N ) = {1, 2, 3, . . .}
2. Man abstrahiert von einer Eigenschaft, die alle
Elemente der Menge haben:
Menge der Primzahlen = {x|x ist nur durch 1
und durch sich selbst teilbar}
• (Darstellung 1. vertraut darauf, dass der Leser die
Abstraktion selber durchführt).
– Typeset by FoilTEX –
4
Mengenoperationen
Mengenoperationen 2
• Es gelten folgende binäre Operationen auf Mengen:
• Das Komplement einer Menge A (A) ist definiert
als: Ā = U − A
1. Vereinigung: A ∪ B = {x|x ∈ A ∨ x ∈ B}
2. Schnitt: A ∩ B = {x|x ∈ A ∧ x ∈ B}
3. Komplementbildung: A − B = {x|x ∈ A ∧ x 6∈
B}
• Vereinigung und Schnitt können generalisiert werden
auf eine beliebige Zahl von Mengen.
Sei S eine Menge von Mengen
S
S = {x|x ∈ S1 ∪ S2 ∪ . . . ∪ Sn ∧ S1, . . . , Sn ∈ S}
T
S = {x|x ∈ S1 ∩ S2 ∩ . . . ∩ Sn ∧ S1, . . . , Sn ∈ S}
– Typeset by FoilTEX –
5
• Komplementgesetze:
1.
2.
3.
4.
A∪A=U
(A) = A
A∩A=∅
A−B =A∩B
• DeMorgans Gesetze:
1. (A ∪ B) = A ∩ B
2. (A ∩ B) = A ∪ B
– Typeset by FoilTEX –
6
Mengenoperationen 3
Folgen
• Es gibt wenigstens zwei binäre Operationen auf
Mengen.
• Eine Folge ist eine geordnete Liste von Elementen.
• Die Kardinalität einer Menge A (|A|) bezeichnet
die Anzahl der Elemente von A (As Mächtigkeit).
|A| = Σx∈A
Folge1: (1,2,3,4,5)
Folge2: (Moses, Josua, Ruth, Samuel)
Folge3: (1, Moses, 2, Josua, 3, Ruth)
• Folgen sind geordnet, doppelte Elemente sind nicht
redundant.
• Die Potenzmenge von A (2A oder P(A)) ist die
Menge aller Teilmengen von A.
(1,2,3,4,5) 6= (3,1,2,5,4)
(1,2,3,4,5) 6= (1,1,2,3,4,4,4,5)
P(A) = {x|x ⊆ A}
• Folgen können endlich oder unendlich sein. Eine
endliche Folge nennt man ein Tupel. Ein Tupel mit
k Elementen nennt man ein k-Tupel.
– Typeset by FoilTEX –
7
– Typeset by FoilTEX –
8
Folgen 2
Relationen
• Wenn A und B Mengen sind, dann ist das Kartesische Produkt (oder Kreuzprodukt) aus A und B
(A × B) definiert als die Menge aller 2-Tupel deren
erstes Element aus A und deren zweites Element
aus B ist.
• Eine Relation R zwischen den Mengen A und B
ist eine Teilmenge von A × B.
A × B = {(x, y)|x ∈ A ∧ y ∈ B}
• Das Kartesische Produkt kann auf n Stellen generalisiert werden.
A1 × . . . × An = {(x1, . . . , xn)|xi ∈ Ai, 1 ≤ i ≤ n}
• Ist eines der Ai leer, so ist auch das Produkt die
leere Menge.
• Das n-fache Kartesische Produkt, bei dem alle Ai
gleich A sind, schreibt man auch als An.
– Typeset by FoilTEX –
9
• Beispiel: Sei A = {a, b, c} und B = {1, 2, 3}, dann
ist R1 = {(a, 1), (a, 2), (b, 3), (c, 1), (c, 3)} eine Relation zwischen A und B.
• R1 ist binär. Relationen können k-stellig sein. Sie
sind dann Teilmengen des Kartesischen Produkts
A1 × . . . × Ak .
• Das Inverse einer Relation R ⊆ A × B, bezeichnet
als R−1 ⊆ B × A, ist definiert als
R−1 = {(b, a)|(a, b) ∈ A × B}
• Ein Pfad in einer binären Relation R ist eine Folge
(a1, . . . , an) mit n ≥ 1, so dass (ai, ai+1) ∈ R für
i = 1, . . . , n − 1.
– Typeset by FoilTEX –
10
Eigenschaften von Relationen
Funktionen
• Eine Relation R ⊆ A × A ist
1. reflexiv gdw.: (a, a) ∈ R für jedes a
2. transitiv gdw.: (a, b) ∈ R ∧ (b, c) ∈ R ⇒ (a, c) ∈
R
3. symmetrisch gdw.: (a, b) ∈ R ⇒ (b, a) ∈ R
4. asymmetrisch gdw.: (a, b) ∈ R ⇒ (b, a) 6∈ R
5. antisymmetrisch gdw.: (a, b) ∈ R ∧ a 6= b ⇒
(b, a) 6∈ R
• Eine Funktion von einer Menge A nach einer Menge
B ist eine binäre Relation R zwischen A und B mit
folgender Eigenschaft: für jedes a ∈ A gibt es genau
ein b ∈ B, so dass (a, b) ∈ R.
R1 = {(x, y)|x ist ein Vater und y ist ein Kind}
R2 = {(y, x)|x ist ein Vater und y ist ein Kind}
• R2 ist eine Funktion, R1 nicht.
• Eine Relation die reflexiv, symmetrisch und transitiv
ist, nennt man Äquivalenzrelation.
– Typeset by FoilTEX –
11
– Typeset by FoilTEX –
12
Funktionen 2
Arten von Funktionen
• Man schreibt eine Funktion f von A nach B oft als
f : A 7→ B.
1. A ist die Domäne von f .
2. B ist der Zielbereich von f .
3. f (a) ist das Abbild von a unter f .
• Das Abbild einer Menge A unter f wird geschrieben
als f [A].
• Eine Funktion f : A 7→ B heißt
1. injektiv, gdw. für jedes b ∈ B existiert höchstens
ein a ∈ A, so dass f (a) = b.
2. surjektiv, gdw. für jedes b ∈ B existiert mindestens ein a ∈ A, so dass f (a) = b.
3. bijektiv, gdw. für jedes b ∈ B existiert genau ein
a ∈ A, so dass f (a) = b (f ist bijektiv gdw. f
injektiv und surjektiv ist).
f [A] = {f (a)|a ∈ A}.
– Typeset by FoilTEX –
13
– Typeset by FoilTEX –
14
Inverse Funktionen
Funktionale Komposition
• Funktionen sind Relationen, haben also auch ein
Inverses. Allerdings ist das Inverse einer Funktion
nicht notwendigerweise wieder eine Funktion.
• f : A 7→ B und g : B 7→ C können komponiert
werden zu einer Funktion h : A 7→ C (oder g ◦ f ).
h nimmt ein a ∈ A, macht damit das, was f damit
getan hätte, und wendet g auf das Ergebnis von
f (a) an.
• Man schreibt das Inverse einer Funktion f : A 7→ B
als f −1 : B 7→ A.
• Für jedes a ∈ A gilt: h(a) = (g ◦ f )(a) = g(f (a))
• Das Inverse einer bijektiven Funktion f ist immer
eine bijektive Funktion f −1, die Umkehrfunktion
von f .
• Das Inverse einer nicht-bijektiven Funktion ist niemals eine Funktion.
– Typeset by FoilTEX –
15
• In diesem Falle existiert nur (g ◦f ) aber nicht (f ◦g),
weil der Wertebereich von g nicht gleich der Domäne
von f ist.
• Wenn aber f : A 7→ A und g : A 7→ A, dann
existieren sowohl (g ◦ f ) als auch (f ◦ g).
– Typeset by FoilTEX –
16
Beweis durch Widerspruch
Endliche und unendliche Mengen
• Ein wichtiges Beweisschema ist der Beweis durch
Widerspruch.
• Mengen A und B sind gleich mächtig, wenn es eine
Bijektion zwischen A und B gibt.
• Beweis von Hypothese H durch Widerspruch:
• Eine Menge A ist endlich, wenn es eine Bijektion
zwischen A und {1, . . . , n} gibt, für eine natürliche
Zahl n ∈ N .
1. Nimm an, es gelte die Negation von H: H 0
2. Leite dann unter dieser Annahme durch logische
Schlußfolgerungen einen Widerspruch ab.
3. Das einzige, was in dieser Ableitung zum Widerspruch geführt haben kann, ist die Annahme, dass
H 0 gilt.
4. Daher muss H 0 falsch sein (H 0 kann nicht richtig
sein, und eine dritte Möglichkeit gibt es nicht).
q.e.d.
5. Wenn H 0 falsch ist, dann ist H wahr.
• Das Schema beruht auf der Annahme, dass H/H 0
nicht gleichzeitig wahr und falsch sein können.
– Typeset by FoilTEX –
17
• Eine Menge A ist unendlich, wenn sie nicht endlich
ist.
• Beispiele für unendliche Mengen: die natürlichen
Zahlen, die ganzen Zahlen, die Primzahlen, die reellen Zahlen, . . .
• Sind alle unendlichen Mengen gleich mächtig (d.h.
kann man immer eine Bijektion zwischen solchen
Mengen finden)?
– Typeset by FoilTEX –
18
Abzählbarkeit
Überabzählbare Mengen und
Diagonalisierung
• Eine Menge A ist
1. abzählbar, wenn
(a) A endlich ist, oder
(b) A abzählbar unendlich ist.
2. abzählbar unendlich, wenn A gleich mächtig ist
wie N (es gibt Bijektion zwischen A und N ).
3. überabzählbar, wenn A nicht abzählbar ist.
• Beispiele für abzählbar unendliche Mengen:
1. die geraden Zahlen
2. die ganzen Zahlen
3. die Vereinigung zweier abzählbar unendlicher
Mengen
4. . . .
– Typeset by FoilTEX –
19
• Nicht alle unendlichen Mengen sind abzählbar. Dies
kann man durch Cantors (Georg Cantor, 1845-1918;
deutscher Mathematiker) Diagonalisierungsprinzip zeigen (siehe Cantor 1890).
• Diagonalisierungsprinzip:
Sei R ⊆ A × A eine binäre Relation und sei D die
Diagonalisierungsmenge für A: D = {a|(a, a) 6∈ R}.
Für jedes a ∈ A sei Ra = {b|b ∈ A ∧ (a, b) ∈ R}.
Dann ist D verschieden von jedem Ra.
• Das Diagonalisierungsprinzip ist anwendbar auf endliche und unendliche Mengen.
– Typeset by FoilTEX –
20
Cantors Diagonalisierungstheorem
Vollständige Induktion
• Theorem: Die Menge 2N ist überabzählbar unendlich.
• Hypothese: Eigenschaft P gilt für alle natürlichen
Zahlen.
• Beweis durch Widerspruch:
• Beweis: erfolgt üblicherweise durch das Prinzip der
vollständigen Induktion.
1. Angenommen 2N sei abzählbar unendlich. Dann
existiert eine Bijektion von N nach 2N (d.h., man
kann jedes Element von 2N mit einer natürlichen
Zahl indizieren): 2N = {R0, R1, R2, . . .}.
2. Bilde die Diagonalmenge D = {n ∈ N |n 6∈ Rn}.
3. D enthält nur natürliche Zahlen, muss also in 2N
sein.
4. Also muss es ein k ∈ N geben, so dass D = Rk .
5. Das kann aber nicht sein, da D 6= Rk , für jedes k
(nach Konstruktion von D). Man hat also einen
Widerspruch.
6. Dann muss die Annahme, dass 2N abzählbar
unendlich ist, falsch sein.
q.e.d.
– Typeset by FoilTEX –
21
• Schema der vollständigen Induktion:
1. Zeige, dass P für 0 (oder 1) gilt (Induktionsanfang).
2. Nimm an, dass P für eine beliebige natürliche
Zahl n gilt (Induktionsannahme).
3. Zeige, dass P für n + 1 gilt (Induktionsschritt).
– Typeset by FoilTEX –
22
Induktionsbeweis 1. Beispiel
Induktionsbeweis 1. Beispiel, 2
• Beobachtung:
• Fortsetzung
1 = 1 = 12
1 + 3 = 4 = 22
1 + 3 + 5 = 9 = 32
1 + 3 + 5 + 7 = 16 = 42
Induktionsschritt:
Pn+1
k=1 (2k − 1) =
Pn
k=1 (2k − 1) + (2(n + 1) − 1) =
Pn
k=1 (2k − 1) + (2n + 1) = (wegen Voraussetzung)
• Zeige: Für alle natürlichen Zahlen n ≥ 1 gilt
Pn
2
k=1 (2k − 1) = n .
n2 + 2n + 1 =
• Beweis (Franciscus Maurolicus, 1494-1575): durch
vollständige Induktion über n.
(n + 1)2
q.e.d.
Induktionsanfang (n = 1):
P1
2
k=1 (2k − 1) = 1 = 1
Induktionsvoraussetzung:
Pn
Es gilt k=1(2k − 1) = n2.
– Typeset by FoilTEX –
23
– Typeset by FoilTEX –
24
Induktionsbeweis 2. Beispiel
Induktionsbeweis 2. Beispiel, 2
• Zeige: |P(M )| = 2n, wenn |M | = n.
• Fortsetzung
Induktionsschritt:
• Beweis: durch vollständige Induktion über n.
Induktionsanfang (n = 0):
1. Wenn M = ∅, dann |M | = 0.
2. Dann ist P(M ) = {∅}, denn nur die leere Menge
ist Teilmenge der leeren Menge.
3. Dann ist |P(M )| = 1 = 20.
Induktionsvoraussetzung:
Sei |M | = n und es gelte |P(M )| = 2n.
– Typeset by FoilTEX –
25
1. Sei |M | = n+1 und sei x ein bestimmtes Element
in M .
2. Teile P(M ) auf in
(a) alle A ∈ P(M), so dass x 6∈ A
(b) alle B ∈ P(M), so dass x ∈ B
3. Nach Vorraussetzung ist die Anzahl der A ∈
P(M) = 2n (alle As sind Teilmengen einer Menge mit n Elementen; x fehlt!).
4. Aus allen Bs kann man x entfernen. Das ändert
die Anzahl der Bs nicht, aber danach handelt es
sich auch bei den Bs um Teilmengen einer Menge
mit n Elementen. Also gilt nach Voraussetzung,
dass die Anzahl aller B = 2n
5. Addiere die Anzahl der As und Bs: 2n + 2n =
2n+1
q.e.d.
– Typeset by FoilTEX –
26
Schubfachprinzip
Abschlusseigenschaften
• Schubfachprinzip (pigeon hole principle): Wenn A
und B endliche Mengen sind, und wenn |A| > |B|,
dann gibt es keine injektive Funktion f : A 7→ B.
• Eine Menge B ⊆ D heißt abgeschlossen unter einer Relation R ⊆ Dn+1 wenn für alle
b1, . . . , bn+1 gilt: Wenn b1, . . . , bn ∈ B und wenn
(b1, . . . , bn, bn+1) ∈ R, dann gilt auch bn+1 ∈ B.
• Beweis: durch vollständige Induktion über |B|.
Induktionsanfang (|B| = 0): Dann existiert f : A 7→
B nicht und kann auch nicht injektiv sein.
Induktionvoraussetzung: Es gibt kein injektives f :
A 7→ B für |B| = n, wenn |A| > |B|.
Induktionsschritt: Sei |A| > |B| und |B| = n + 1.
Betrachte a ∈ A. Wenn es a0 ∈ A gibt, so dass
a 6= a0 und f (a) = f (a0), dann ist f nicht injektiv.
Falls kein solches a0 ∈ A existiert, betrachte g :
A − {a} 7→ B − {f (a)}, wobei g sonst wie f ist.
Nach Voraussetzung ist g aber nicht injektiv. Also
ist f auch nicht injektiv.
q.e.d.
– Typeset by FoilTEX –
27
• Eine Eigenschaft der Form “die Menge B ist abgeschlossen unter der Relation R” nennt man eine
Abschlusseigenschaft von B.
• Beispiel: N ist abgeschlossen unter Addition, Multiplikation, und Quadratur, aber nicht unter Subtraktion, Division, oder dem Ziehen der Quadratwurzel.
• Abschlusseigenschaften können benutzt werden, um
aus kleineren Mengen größere zu konstruieren.
• Der reflexiv transitive Abschluss (reflexiv transitive Hülle) einer Relation R ⊆ A2 ist die Relation
R∗ = {(a, b)|a, b ∈ A und es gibt einen Pfad von a
nach b in R}.
– Typeset by FoilTEX –
28
Literatur
Cantor, Georg (1890): ‘Über eine elementare Frage der
Mannigfaltigkeitslehre’, Deutsche MathematikerVereinigung 1, 75–78.
Halmos, Paul (1976): Naive Mengenlehre. Vandenhoeck & Ruprecht, Göttingen.
– Typeset by FoilTEX –
29