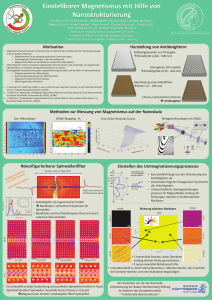
Spinwellen in Ni81Fe19-Nanostreifen mit kontrollierten Dom¨anenw

Spinwellen in Ni81Fe19-Nanostreifen mit
kontrollierten Domänenwänden
DIPLOMARBEIT
in
Experimentalphysik
von
Christian Werner Sandweg
durchgeführt am
Fachbereich Physik
der Technischen Universität Kaiserslautern
unter Anleitung von
Prof. Dr. B. Hillebrands
September 2007
1
”
...insane in the membrane.“
(Cypress Hill, Black Sunday, 1993)
i
Inhaltsverzeichnis
1
Einleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
2
Theoretische Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.1 Magnetisierungsdynamik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.1.1 Landau-Lifschitz- und Gilbert-Gleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.1.2 Das effektive Magnetfeld . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.2 Spinwellen. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.2.1 Magnetostatische Oberflächenmode. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.2.2 Magnetostatische Backward“-Volumenmode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
”
2.2.3 Quantisierte Spinwellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.3 Domänenwände in weichmagnetischen Nanostreifen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
3
Experimenteller Aufbau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
3.1 Brillouin-Lichtstreuspektroskopie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
3.1.1 Generelle Funktionsweise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
3.1.2 Brillouin-Lichtstreumikroskopie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.2 Lorentzmikroskopie. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
4
Probenpräparation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
4.1 Herstellung der Proben für die Untersuchung im Lorentzmikroskop . . . . . . . . . . . . . . . 32
4.2 Eigenschaften der Proben für die Untersuchungen im Brillouin-Lichtstreumikroskop und deren Herstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
4.2.1 Eigenschaften der Proben . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
4.2.2 Herstellung der Proben . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
5
Experimentelle Ergebnisse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
5.1 Charakterisierung der Domänenwandstrukturen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
5.1.1 Lorentz-Mikroskopie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
5.1.2 Parametervariation mittels mikromagnetischer Simulation. . . . . . . . . . . . . . . . . . 49
5.2 Charakterisierung des Spinwellenspektrums . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
5.2.1 Untersuchung des thermischen Spinwellenspektrums. . . . . . . . . . . . . . . . . . . . . . . 52
5.2.2 Untersuchung angeregter Spinwellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
ii
INHALTSVERZEICHNIS
6
Zusammenfassung und Ausblick. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
Literaturverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
iii
KAPITEL 1
Einleitung
In Zeiten beständig wachsender Anforderungen an die technischen Fähigkeiten moderner Computer und dem gleichzeitigen Erreichen physikalischer Grenzen der bisher genutzten Technologien
müssen neue Wege gefunden werden, um sowohl die Speicherdichten als auch die Verarbeitungsgeschwindigkeit elektronisch gespeicherter Daten weiter zu erhöhen. Während magnetische Materialien seit jeher das Speichermedium für größere Datenmengen auf Festplatten bilden, dringt
der Magnetismus in Form von magnetic random access memories (MRAM) auch in bislang von
Halbleitern dominierten Bereichen der Datenverarbeitung vor [1]. Zusätzlich werden bereits Konzepte erarbeitet und bereits auch schon experimentell realisiert, die den Spin, einen bislang noch
überhaupt nicht genutzten Freiheitsgrad des Elektrons, zur Herausbildung einer neuen Elektronik,
der Spinelektronik oder kurz Spintronik, nutzen [2]. Damit zusammen hängt auch die Verwirklichung neuer nicht mehr auf Halbleitern basierender Logikbausteine. Die Gruppe um Prof. Russell
Cowburn vom Imperial College London präsentierte bereits den Entwurf von Logikschaltungen,
bei denen die logischen Zustände 0 und 1 durch das Verschieben von Domänenwänden erreicht
werden kann [3, 4]. Das Phänomen der Domänenwände in magnetischen Strukturen ist bereits seit
langem bekannt und ausführlich beschrieben worden [5]. Felix Bloch entdeckte bereits 1932 [6],
Louis Néel 1955 [7] die später nach ihnen benannten Domänenwandtypen. In der Vergangenheit
lag der Schwerpunkt der Forschung auf der Untersuchung von Domänenwandresonanzen, Eigenschaften sich bewegender Wände sowie der Bestimmung der Domänenwandgeschwindigkeit und
ihrer effektiven Masse [8–10]. Zu dieser Zeit waren Untersuchungen auf so genannte bubble garnet
materials wie beispielsweise Yttrium-Eisen-Granat beschränkt [11]. Seit dem Beginn der neunziger Jahre kam dem Gebiet neue Aufmerksamkeit zu, und führten zu den bereits weiter oben
erwähnten vorgeschlagenen Anwendungen. Die jüngere Forschung weist dabei weniger auf Anwendung bedachte, aber physikalisch außerordentlich interessanter Resultate wie das von Saitoh
et al. hergestellte Domänenwandpendel auf.
Eines der bislang am wenigsten untersuchten Gebiete in diesem Zusammenhang ist die Wechselwirkung zwischen Spinwellen und Domänenwänden. Grundlagenphysikalisch ist dabei zunächst
interessant, dass Spinwellen von Domänenwänden nicht reflektiert werden sollten, sondern die
1
Wand lediglich mit einer Phasenverschiebung durchdringen [12]. Andererseits birgt die genauere
Untersuchung der dabei auftretenden Effekte das Potential einer anderen Art von magnetischer
Logik in sich, die auf der Interferenz zweier zueinander phasenverschobener Spinwellen basiert.
Das größte Hindernis bei der bisherigen Untersuchung solcher Effekte war der Mangel an geeigneten Techniken. Durch die Entwicklung der Brillouin-Lichtstreumikroskopie ist es nun jedoch
möglich, mit geeigneter Auflösung das Verhalten der Spinwellen und ihre Wechselwirkung mit
Domänenwänden zu untersuchen. Während dieser Arbeit wurden daher zunächst geeignete Probenstrukturen für die spätere Untersuchung entwickelt und hergestellt, mit verschiedenen Methoden charakterisiert und schließlich erste Messungen zum Verhalten der Spinwelle in An- bzw.
Abwesenheit einer Domänenwand durchgeführt.
In Kapitel 2 werden die theoretischen Grundlagen zum späteren Verständnis der experimentellen
Ergebnisse dargelegt. Dabei wird zuerst ein Überblick über die Magnetisierungsdynamik gegeben
und die Landau-Lifschitz- und Gilbert-Gleichung vorgestellt, anschließend genauer auf Spinwellen eingegangen. Zusätzlich werden in den theoretischen Grundlagen die verschiedenen Arten von
Domänenwänden in weichmagnetischen Nanostreifen präsentiert.
Im nächsten Kapitel werden die im Rahmen dieser Diplomarbeit verwendete Brillouin-Lichtstreumikroskopie und die Lorentzmikroskopie vorgestellt. In diesem Zusammenhang wird noch einmal
speziell auf die Brillouin-Lichtstreumikroskopie eingegangen, mit deren Hilfe das Spektrum thermisch aktivierter und angeregter Spinwellen beobachtet wurde. Die Lorentzmikroskopie wurde im
Rahmen einer Kooperation an der Univertät Glasgow durchgeführt.
Kapitel 4 beschäftigt sich mit der Präparation der Proben, die für diese Diplomarbeit verwendet wurde. Dabei wurden für die Brillouin-Lichtstreumikroskopie und die Lorentzmikroskopie
zwei verschiedene Arten von Proben hergestellt, die sich in ihren Spezifikationen mitunter deutlich unterscheiden. Die Entwicklung spezieller Proben für die Lorentzmikroskopie war, wie später
noch ausführlich beschrieben wird, durch die speziellen Probenanforderungen dieser Messmethode vonnöten.
Die in dieser Diplomarbeit erzielten experimentellen Ergebnisse werden schließlich in Kapitel 5
vorgestellt. Dabei wurde die Lorentzmikroskopie eingesetzt, um genaue Einblicke in das Aussehen
und die Struktur von Domänenwänden gewinnen zu können. Mit Hilfe der Brillouin-Lichtstreumikroskopie wurde untersucht, welche Auswirkungen das Passieren einer Domänenwand auf eine einlaufende Spinwelle hat. Zunächst wurde dazu das Spektrum thermisch aktivierter Spinwellen aufgenommen, um das Eigenmodenspektrum der untersuchten Strukturen zu bekommen.
Zusätzlich konnte dabei bereits festgestellt werden, ob das Spektrum durch das Vorhandensein
einer Domänenwand verändert wird. Zum Schluss wurden ebenfalls mit der Brillouin-Lichtstreumikroskopie durch Mikrowellenströme angeregte Spinwellen untersucht. Das Interesse lag dabei
auf der Wechselwirkung von kohärenten Spinwellen mit Domänenwänden, wobei die kohärente
2
Anregung durch die externe Anregung von Spinwellen durch eine Mikrowellenantenne sichergestellt wurde.
Kapitel 6 schließt die Arbeit mit der Zusammenfassung der während des letzten Jahres erzielten
Ergebnisse sowie einem Ausblick auf die weiter auf diesem Gebiet zu unternehmenden Anstrengungen.
3
KAPITEL 2
Theoretische Grundlagen
In diesem Kapitel werden die theoretischen Grundlagen erläutert, die für das Verständnis der experimentellen Ergebnisse in Kapitel 5 notwendig sind. Alle hier verwendeten Gleichungen sind im
cgs-System angegeben. Eine entsprechende Umrechnung vom cgs- in SI-System kann beispielsweise in Ref. [13] gefunden werden.
Zuerst werden die Grundlagen der Magnetisierungsdynamik erläutert. Anschließend wird genauer
auf Spinwellen und auf Mechanismen, die zur Quantisierung von Spinwellen führen, eingegangen.
Da die Untersuchung der Wechselwirkung von Spinwellen mit Domänenwänden ein wichtiger Teil
dieser Diplomarbeit ist, wird zum Schluss noch ein Überblick über die verschiedenen Typen von
Domänenwänden in sogenannten Nanostreifen gegeben.
2.1. Magnetisierungsdynamik
Sowohl für weitergehende theoretische Überlegungen, als auch für die Entwicklung neuartiger
magnetischer Speicher und Sensoren ist eine genaue Betrachtung der Magnetisierungsdynamik
von großer Bedeutung.
In erster Näherung wird die Magnetisierung in diesem Unterkapitel als homogen angesehen, d.h.
die Probe ist vollständig in einer Richtung magnetisiert und es liegt keine Domänenstruktur vor.
Damit können grundlegende Erkenntnisse zur Magnetisierungsdynamik gewonnen werden, die
später modifiziert auch auf kompliziertere Magnetisierungen mit Domänen angewandt werden
können. Im Rahmen dieser Vereinfachung dominiert die Austauschwechselwirkung und die Magnetisierung wird dadurch komplett ausgerichtet. Solche Systeme werden als Stoner-Wohlfahrt”
Teilchen“ bezeichnet, die dabei benutzte Approximation als Makrospin“ [14].
”
2.1.1 Landau-Lifschitz- und Gilbert-Gleichung
Das Verhalten der Magnetisierung in einem externen Magnetfeld lässt sich durch die LandauLifschitz- und Gilbert-Gleichung in geeigneter Weise beschreiben. Sie stellt die Bewegungsglei-
4
2.1 Magnetisierungsdynamik
chung der Magnetisierung dar. Im Folgenden wird der von Landau und Lifschitz entwickelte Teil
der Gleichung quantenmechanisch hergeleitet und anschließend die von Gilbert stammende Modifikation der Gleichung erläutert.
Betrachtet man die zeitliche Entwicklung des Erwartungswertes des Spins Ŝ, so lautet die quantenmechanische Beschreibung:
i}
d
< Ŝ >=< [Ŝ,H ] > .
dt
(2.1)
H ist dabei der Hamiltonoperator des Spins in einem zeitabhängigen Magnetfeld H(t) im Vakuum:
H=
gµB
Ŝ · B , wobei B = H(t).
}
(2.2)
Die jeweiligen Komponenten des Spins Sx , Sy und Sz gehorchen dabei den bekannten Vertauschungsrelationen [15]:
[Sx , Sy ] = i}Sz ,
[Sy , Sz ] = i}Sx ,
[Sz , Sx ] = i}Sy .
(2.3)
Dadurch wird die rechte Seite von Gleichung 2.1 zu:


[Sx ,Sx Bx + Sy By + Sz Bz ]
[Ŝ,H ] = gµ}B [Sy ,Sx Bx + Sy By + Sz Bz ]
[Sz ,Sx Bx + Sy By + Sz Bz ]


By [Sx ,Sy ] + Bz [Sx ,Sz ]
gµB 
Bz [Sy ,Sz ] + Bx [Sy ,Sx ]
=
}
Bx [Sz ,Sx ] + By [Sz ,Sy ]


By Sz − Bz Sy
gµB 

=
} i} Bz Sx − Bx Sz .
Bx Sy − By Sx
(2.4)
Daraus folgt:
d
gµB
< Ŝ >= −
< Ŝ > ×B.
dt
}
(2.5)
Interessiert ist man allerdings meistens an der Magnetisierung der jeweiligen Probe. Man erhält sie
durch Summation und Mittelung über das Volumen:
M=
1 X gµB
< Ŝ > .
V
}
(2.6)
V
Das zeitabhängige Magnetfeld H(t) ist dabei das lokale effektive Magnetfeld Heff , das sich aus
allen Feldern zusammensetzt, die an der Magnetisierung angreifen können:
5
2.1 Magnetisierungsdynamik
Heff = H0 + Hext + Hd + Hxc + Hani + . . . .
(2.7)
Dabei sind H0 und Hext die von außen angelegten statischen und dynamischen Magnetfelder,
Hd ist das von den magnetischen Oberflächen- und Volumenladungen durch die Dipol-DipolWechselwirkung erzeugte Entmagnetisierungsfeld. Hxc steht für die Austauschwechselwirkung
und Hani beschreibt die durch die Kristallstruktur verursachten Anisotropien. Weitere Beiträge
zum lokalen effektiven Magnetfeld, wie zum Beispiel die Magnetostriktion oder Exchange-BiasPhänomene sollen im Weiteren nicht betrachtet werden. Zusammen mit der Substitution der einzelnen Spins durch die Magnetisierung in 2.6 ergibt sich nun für die Bewegungsgleichung der
Magnetisierung in einem Magnetfeld:
dM
= −|γ|M × Heff .
dt
√
Der Betrag der Magnetisierung |M̂| = M2 ist dabei zeitlich konstant, denn es gilt:
d 2
d
M = 2M M = −2|γ|M · (M × Heff ) = 0,
dt
dt
(2.8)
(2.9)
Der Winkel zwischen der Magnetisierung und einem zeitlich konstanten Magnetfeld bleibt ebenfalls erhalten
d
d
(M · Heff ) = Heff M = −|γ|Heff · (M × Heff ) = 0.
dt
dt
(2.10)
Die beiden Erhaltungssätze 2.9 und 2.10 sind allerdings noch nicht ausreichend. Die Magnetisierung M würde, einmal ausgelenkt, immer weiter präzedieren, da noch keinerlei Dämpfung
berücksichtigt wurde. Landau und Lifschitz führten aus diesem Grund einen zusätzlichen Dämpfungsterm ein [16]. Damit ergibt sich schließlich die Landau-Lifschitz-Gleichung:
dM
αLL |γ|
= −|γ|M × Heff −
M × (M × Heff ).
dt
Ms
(2.11)
Dabei ist Ms die Sättigungsmagnetisierung des Systems und αLL die Landau-Lifschitz-Dämpfungskonstante. Der Vektor der magnetischen Dämpfung −M × (M × Heff ) ist dabei so konstruiert worden, dass der Vektor in Richtung der Präzessionsachse zeigt, so dass es zu einer Dämpfung kommt.
Die magnetische Dämpfung geschieht dabei durch Energieübertragung vom System präzedierender
Spins auf das Magnonen- und Phononen-System des Festkörpers. Die Energieübertragung auf das
Magnonen-System erfolgt durch Spinwellen, die Übertragung auf das Phononen-System durch
Spin-Bahn-Kopplung. Bei Metallen kann eine zusätzliche Kopplung an freie Elektronen zur magnetischen Dämpfung durch Wirbelströme auftreten.
6
2.1 Magnetisierungsdynamik
Die Landau-Lifschitz-Gleichung 2.11 hat jedoch den wesentlichen Schwachpunkt, dass im Grenzfall großer Dämpfung, d.h. αLL À 1 das Resultat unphysikalisch wird [17]. In diesem Fall nimmt
die Präzessionsfrequenz durch Vergrößerung der Dämpfung zu und könnte damit beliebig gesteigert werden. Gilbert ersetzte daher den vorhandenen Dämpfungsterm durch einen rein phänomenologischen Dissipationsterm [18], der das Auftreten des unphysikalischen Resultats verhindert.
Der Dissipationsterm ist dabei zu der zeitlichen Änderung der Magnetisierung proportional, analog zur Dämpfung in einer viskosen Flüssigkeit, bei der der Dissipationsterm proportional zur
Geschwindigkeit gewählt wird:
H = Heff −
αG dM
.
|γ|Ms dt
(2.12)
Somit ergibt sich schließlich die Landau-Lifschitz- und Gilbert-Gleichung:
dM
αG
dM
= −|γ|M × Heff +
M×
.
dt
Ms
dt
(2.13)
αG ist die sogenannte Gilbert-Dämpfungskonstante und ist der erste Term einer Reihenentwicklung
nach αG0 [19]. Mathematisch äquivalent und für numerische Berechnungen leichter anwendbar ist
folgende Form von 2.13:
dM
αG
|γ|
M
×
H
+
=−
M × (M × Heff ).
e
f
f
dt
MS
1 + α2G
(2.14)
Dabei beschreibt der erste Summand auf der rechten Seite die Larmor-Präzessionsbewegung der
Magnetisierung M im Magnetfeld Heff . Der zweite Summand enthält den Dämpfungsterm und
bewirkt somit die allmähliche Ausrichtung der Magnetisierung entlang der Richtung des effektiven
Magnetfeldes Heff . Auch in Gleichung 2.14 ist der Betrag der Magnetisierung wieder zeitlich
konstant.
2.1.2 Das effektive Magnetfeld
Das bereits vorgestellte effektive Feld Heff ist in der Landau-Lifschitz- und Gilbert-Gleichung
2.13 direkt im Drehmoment enthalten, so dass es direkt die Dynamik des magnetischen Systems
beeinflusst. Aus diesem Grund wird an dieser Stelle noch einmal näher auf die einzelnen Beträge
des effektiven Feldes Heff eingegangen.
Das Entmagnetisierungsfeld
Durch jedes atomare magnetische Moment µm eines Ferromagneten wird ein magnetisches Dipolfeld im Abstand r verursacht [20]:
7
2.1 Magnetisierungsdynamik
Abbildung 2.1:
a) Präzessionsbewegung der Magnetisierung ohne Dämpfungsterm.
b) Gedämpfte Präzessionsbewegung der Magnetisierung. Dabei sind die Richtungen der Drehmomente dargestellt, die aus beiden Termen der Landau-Lifschitz- und Gilbert-Gleichung folgen.
H(r) =
3r(r · µm ) µm
− 3.
r
r5
(2.15)
In einem homogenen Ferromagneten, der unendlich ausgedehnt ist, heben sich nun die einzelnen
magnetischen Momente gegenseitig auf. In einem endlichen System jedoch erzeugen die an den
Oberflächen lokalisierten magnetischen Momente, sofern sie nicht tangential zur Grenzfläche stehen, durch die Dipol-Dipol-Wechselwirkung ein effektives Magnetfeld, das Entmagnetisierungsfeld Hd . Es soll nun im Folgenden berechnet werden. Im Rahmen des magnetostatischen Limits
ergeben sich folgende vereinfachte Maxwell-Gleichungen:
∇×H = 0
(2.16)
∇ · B = ∇ · (H + 4πM)
(2.17)
H ist gemäß Gleichung 2.16 rotationsfrei und kann daher als Gradient eines magnetischen Potentials φM geschrieben werden:
H = −∇φM
(2.18)
Einsetzen in die Gleichung 2.17 liefert nun das magnetostatische Äquivalent zur Poisson-Gleichung
der Elektrostatik
4φM = −ρM ,
(2.19)
mit
8
2.1 Magnetisierungsdynamik
ρM = −4π∇ · M.
(2.20)
ρM kann dabei als magnetische Ladungsdichte interpretiert werden. Im Endlichen ohne Randbedingungen kann die magnetostatische Poisson-Gleichung durch das Poisson-Integral gelöst werden [20]:
Z
φM (r) = −
ρM
dr0 = −
|r − r0 |
Z
∇0 · M(r0 ) 0
dr .
|r − r0 |
(2.21)
Im Fall einer endlichen Magnetisierungsverteilung kann das Integral in zwei Terme aufgespalten
werden:
1
φM (r) = −
4π
Z
V
∇0 · M(r0 ) 0 1
dr +
|r − r0 |
4π
I
∂V
n(r0 ) · M(r0 )
dF 0 .
|r − r0 |
(2.22)
Der erste Term von 2.22 ist ein Volumenintegral und gibt das Potential des Entmagnetisierungsfeldes an. Das Entmagnetisierungsfeld entsteht dabei durch Volumenladungen λM = ∇0 · M(r0 ), die
durch eine inhomogene Magnetisierungsverteilung erzeugt werden. Der zweite Term ist ein Oberflächenintegral und gibt das durch magnetische Oberflächenladungen σM = n(r0 ) · M(r0 ) erzeugte
Potential des Entmagnetisierungsfeldes an.
Werden keine magnetischen Ladungen erzeugt, wird das Volumenintegral über die Energiedichte
Z
Z
εd dr =
1
Hd · M dr
2
(2.23)
minimal. Daher wird die Magnetisierung ohne von außen angelegtes Magnetfeld tangential zu den
Grenzflächen verlaufen und im Volumen wird ∇ · M = 0 gelten. Dieses setzt allerdings voraus,
dass es nicht durch andere Beiträge der Gesamtenergie verhindert wird, wie zum Beispiel durch
Anisotropien oder der Austauschenergie, welche im Folgenden erläutert wird.
Das Austauschfeld
Die Abhängigkeit der Energie eines Spinsystems bezüglich der Orientierung einzelner Spins Si
zueinander wird als Austauschenergie bezeichnet und durch den Heisenberg-Hamilton-Operator
beschrieben:
Eixcj = −2Ji j Si · Sj .
(2.24)
Begründet wird dieser Ausdruck durch das Pauli-Prinzip [21]. Daher ist die Austauschenergie
ein rein quantenmechanischer Effekt. Ji j wird dabei in der Literatur häufig als Austauschintegral
9
2.1 Magnetisierungsdynamik
bezeichnet und ist eine Funktion des Abstands zweier Spins zueinander. Da diese Funktion mit zunehmenden Abstand sehr stark abfällt, ist es in den meisten Fällen ausreichend bei der Berechnung
der Austauschenergie nur die nächsten Nachbarn (NN) zu berücksichtigen. Somit ergibt sich für
die Austauschenergie des i-ten Spins [22]:
Eixc = −2
X
Ji j Si · Sj = −2Si ·
j=NN
X
Ji j Sj =
j=NN
2µi X
·
Ji j Sj
gµB
(2.25)
j=NN
Damit kann man nun die Austauschenergie als Zeeman-Energie des magnetischen Momentes µi
im sogenannten Austauschfeld beschreiben:
Hxc = −
2 X
Ji j Sj
gµ0 µB
(2.26)
j=NN
Wichtig ist nun, die Summe aus Gleichung 2.26 so umzuformen, dass sie in die Landau-Lifschitzund Gilbert-Gleichung 2.13 einsetzbar ist. Dafür werden alle Spins durch ein Vektorfeld S(r) dargestellt:
X
Sj =
j=NN
X
S(ri + rij ).
(2.27)
j=NN
ri ist dabei der Ort, an dem das Austauschfeld berechnet wird und rij ist der Abstandsvektor zum
nächsten Spin. Somit gilt für ein einfach kubisches Gitter:
X
S(ri + rij ) = S(ri + ax̂) + S(ri − ax̂)
j=NN
+ S(ri + aŷ) + S(ri − aŷ)
+ S(ri + aẑ) + S(ri − aẑ),
(2.28)
wobei a die Gitterkonstante ist. Bei kleineren Verkippungen der Spins gegeneinander lässt sich die
zweite Ableitung der Vektorfunktion S(r) folgendermaßen annähern:
∂2 S(r)
1
≈ 2 [S(ri + ax̂) − 2S(ri ) + S(ri − ax̂)] .
2
∂x
a
(2.29)
Damit ergibt sich 2.28 zu:
X
j=NN
·
2
S(ri + rij ) ≈ a
∂2 S ∂2 S ∂2 S
+
+
∂x2 ∂y2 ∂z2
¸
+ 6S(ri )
r=ri
= a2 ∇2 S(ri + rij ) + 6S(ri + rij ).
(2.30)
10
2.2 Spinwellen
Zusammen mit Gleichung 2.20 ergibt sich damit für das Austauschfeld:
Hxc =
¤
2Ji j £
2 2
6M
+
a
∇
M
.
2
µ0 µB Ng2
(2.31)
Genau genommen gilt Gleichung 2.31 nur für kubische Gitter. Auch ist Gleichung 2.29 für Grenzflächen nicht mehr gültig, da in diesem Fall zusätzliche Randbedingungen angenommen werden
müssen. Eine ausführliche Rechnung ist in Ref. [23] zu finden. Gleichung 2.31 kann noch einmal
vereinfacht werden, da der Term, der proportional zu M ist, wegen M × M = 0 keinen Beitrag zum
Drehmoment liefert. Damit erhält man schließlich:
Hxc = λex ∇2 M.
(2.32)
λxc ist die sogenannte Austausch-Steifigkeitskonstante.
2.2. Spinwellen
Die Dynamik eines Spins wird durch die Landau-Lifschitz- und Gilbert-Gleichung 2.13 beschrieben. Im Rahmen der Makrospin-Näherung kann jedoch auch die Dynamik einer kohärenten Präzession über die gesamte Länge einer homogen magnetisierten Probe mit dieser Gleichung beschrieben werden. Bei Spinwellen gilt der Spezialfall, dass der Wellenvektor k gleich null und somit die
Wellenlänge unendlich ist, nicht mehr. Dabei sind die Spins immer parallel zueinander ausgerichtet und damit ist die Austauschwechselwirkung vernachlässigbar. Um nun die Präzessionsfrequenz
der Magnetisierung und somit auch die Resonanzfrequenz des Systems zu berechnen, wird im Folgenden die Landau-Lifschitz- und Gilbert-Gleichung 2.13 zusammen mit den magnetostatischen
Maxwell-Gleichungen 2.16 und 2.17 gelöst. Betrachtet wird dazu ein in z-Richtung magnetisierter
und unendlich ausgedehnter isotroper Körper. Die Magnetisierung und das effektive Feld werden
in ihre statischen und dynamischen Anteile zerlegt:

mx eiωt
M = M0 + m(t) =  my eiωt 
M0


hx eiωt
H = H0 + h(t) =  hy eiωt 
H0

(2.33)
(2.34)
Zur Vereinfachung wird für die dynamischen Komponenten der Magnetisierung und des Magnetfeldes eine harmonische Zeitabhängigkeit angenommen. Zusätzlich sollen die Amplituden im Vergleich zur statischen Komponente sehr klein sein:
11
2.2 Spinwellen
mx ,my ¿ M0
und
hx ,hy ¿ H0
(2.35)
Verwendet man nun 2.33 und 2.34 unter Berücksichtigung der Annahmen in 2.35, so kann die
Landau-Lifschitz- und Gilbert-Gleichung 2.13 linearisiert werden. Die Lösung ist die sogenannte
Kittel-Formel [24]:
ν=
γ p
(H0 + 4πMs )H0
2π
(2.36)
Bei Spinwellen mit einer endlichen Wellenlänge gilt jedoch 2.36 nicht mehr, da benachbarte Spins
gegeneinander verkippt sind und sowohl die Austausch- als auch die Dipolwechselwirkung gemäß
2.36 die Dynamik des Systems beeinflussen. Daher wird unter Berücksichtigung von 2.35 die jetzt
ortsabhängige dynamische Magnetisierung m(R,t) in ebene Wellen entwickelt:
m(R,t) =
X
mk (t)eikR
(2.37)
k
Dabei wird über alle dreidimensionalen Wellenvektoren k summiert. Da sich die Amplituden der
ebenen Wellen für verschiedene Wellenvektoren unterscheiden können, gilt m(t) = mk (t). Die harmonische Zeitabhängigkeit bleibt erhalten. Da die dynamische Magnetisierung nun ortsabhängig
ist, wirkt auf sie der Differentialoperator ∇2 aus 2.32 des Austauschfeldes:
Hex = λex ∇2 M = λex ∇2 [M0 + m(R,t)] = −λex k2 m(R,t)
(2.38)
Die Lösung der Landau-Lifschitz- und Gilbert-Gleichung 2.13 unter Einbeziehung von Gleichung
2.37 ist die sogenannte Herring-Kittel-Formel [25]:
γ
ν=
2π
q
¡
¢
(H0 + λex k2 ) H0 + λex k2 + 4πMs sin2 θk .
(2.39)
θk ist der Winkel zwischen dem Wellenvektor und der statischen Magnetisierung. Gegenüber der
Kittel-Formel 2.36 hat sich aufgrund der Austauschwechselwirkung das effektive Magnetfeld H0
um λex k2 erhöht. Im Fall großer Wellenvektoren, d.h. für
λex k2 À H0 + 4πMs
(2.40)
ist die Spinwellenfrequenz nun vom Quadrat des Wellenvektors abhängig.
12
2.2 Spinwellen
2.2.1 Magnetostatische Oberflächenmode
Die im letzten Abschnitt beschriebene Herring-Kittel-Formel beschreibt das Spinwellenspektrum
eines unbegrenzten ferromagnetischen Körpers. Bei Betrachtung einer dünnen Schicht magnetischen Materials der Dicke d ergeben sich zwei Unterschiede zum bereits besprochenen Modellsystem: Zum einen führen Reflexionen der Spinwellen an den Grenzen der Struktur zur Ausbildung
stehender Wellen und damit zur Quantisierung der Wellenvektoren senkrecht zur Schichtebene,
zum anderen werden magnetostatische und dynamische Oberflächenladungen durch die dynamischen Komponenten der Magnetisierung an den Grenzflächen erzeugt. Bei einer Propagationsrichtung der Spinwelle senkrecht zur statischen Magnetisierung, d.h. θk = 90◦ , spricht man von einer
magnetostatischen Oberflächenmode“(MSSW)1 . Diese Mode wird, nach R.W. Damon und J.R.
”
Eshbach, die ihr Spektrum zuerst berechneten, auch Damon-Eshbach-Mode genannt [26]. Die Amplitude der dynamischen Magnetisierung fällt über die Schichtdicke exponentiell ab, wobei die Abklinglänge in der Größenordnung der Wellenlänge ist. Auch hat die MSSW eine Vorzugsrichtung
des Umlaufsinns auf der Probenoberfläche. Für Schichtdicken unter 20 nm ist der exponentielle
Abfall der Präzessionsamplitude vernachlässigbar. Das Profil der dynamischen Magnetisierung ist
in diesem Fall über die Schichtdicke nahezu konstant. Für die von Damon und Eshbach berechnete
Dispersionsrelation der magnetostatischen Oberflächenmode gilt:
νMSSW
γ
=
2π
q
H(H + 4πMs ) + (2πMs )2 (1 − e−2kk d )
(2.41)
Abbildung 2.2 aus Ref. [27] zeigt die Dispersionsrelation einer Damon-Eshbach-Mode für den
Wellenvektorbereich von kk = 0 bis kk = 2 · 105 cm−1 . Die Dispersionsrelation ist in diesem
Bereich durch die dipolare Wechselwirkung dominiert. Erst für kk · d À 1 ist die Austauschenergie
nicht mehr vernachlässigbar und führt schließlich zu einer quadratischen Dispersion.
1 engl.:
Magnetostatic Surface Wave
13
2.2 Spinwellen
qk = 90°
20
Frequenz [GHz]
18
16
14
12
M
10
8
k
MSSW
0
10
20
Wellenvektor senkrecht zu M [104/cm]
Abbildung 2.2:
Dispersion für magnetostatische Oberflächenmoden“, d.h. die Ausbreitungsrichtung der Spinwelle ist
”
senkrecht zur statischen Magnetisierung. Die Austauschwechselwirkung wurde dabei nicht berücksichtigt.
2.2.2 Magnetostatische Backward“-Volumenmode
”
Ist die Propagationsrichtung einer Spinwelle parallel zur statischen Magnetisierung, d.h. θk = 0◦
so spricht man von einer magnetostatischen Backward“-Volumenmode (MSBVW)2 . Im Unter”
schied zur MSSW, die durch das exponentielle Abklingen der dynamischen Magnetisierung an
der Oberfläche lokalisiert ist, hat die MSBVW ein über die Schichtdicke nahezu konstantes Profil.
Bei kk = 0 beginnt die Dispersionsrelation der MSBVW bei der gleichen Frequenz, der FMRFrequenz, wie die MSSW, siehe Abbildung 2.3 aus [27]. Allerdings hat die MSBVW bei kleinen Wellenvektoren, im Gegensatz zur MSSW, eine negative Steigung. Da somit die Gruppengeschwindigkeit der Spinwellen in dieser Geometrie negativ, also der Phasengeschwindigkeit entgegengerichtet ist, werden diese Moden als Backward“-Volumenmoden bezeichnet. Für diesen
”
Bereich kann die Dispersionsrelation der MSBVW folgendermaßen angenähert werden [25]:
νMSBVW
v Ã
!
u
−kk d
γ u
1
−
e
= tH H + 4πMs
2π
kk d
(2.42)
Erst für Wellenvektoren, für die kk · d À 1 gilt, ist aufgrund der nicht mehr vernachlässigbaren
Austauschwechselwirkung die Dispersionskurve und damit die Gruppengeschwindigkeit wieder
positiv und nimmt schon wie die MSSW einen quadratischen Verlauf an.
2 engl.:
Magnetostatic Backward Volume Mode
14
2.2 Spinwellen
qk = 0°
8,6
M
k
Frequenz [GHz]
8,4
8,2
8,0
7,8
7,6
MSBVW
0
10
20
4
Wellenvektor parallel zu M [10 /cm]
Abbildung 2.3:
Dispersion einer magnetostatischen Backward“-Volumenmode, bei der die Ausbreitungsrichtung para”
llel zur statischen Magnetisierung ist. Die Austauschwechselwirkung wurde dabei, wie schon zuvor nicht
berücksichtigt.
2.2.3 Quantisierte Spinwellen
Durch die Einschränkung einer Welle auf ein begrenztes Volumen wird die Energie der Welle quantisiert. Im Falle von Spinwellen kann diese Begrenzung zwei mögliche Ursachen haben. Zum einen
kann durch eine Reduzierung des magnetischen Volumens auf die Größenordnung der SpinwellenWellenlänge und zum anderen durch ein inhomogenes effektives Magnetfeld eine Quantisierung
der Energie erfolgen. Beide Mechanismen wurden experimentell zuerst in lateral strukturierten
Systemen mittels Brillouin-Lichtstreumikroskopie nachgewiesen [28–30].
Quantisierung durch Begrenzung des magnetischen Volumens
Man betrachte einen magnetischen Streifen der Länge L, der Breite w und der Dicke d. Dabei liegt
die kurze Seite parallel zur z-Achse eines kartesischen Koordinatensystems und die lange Seite parallel zur y-Achse. Ist nun der Streifen entlang der langen Seite, also in y-Richtung magnetisiert, so
können die durch magnetische Oberflächenladungen an den Streifenenden hervorgerufenen magnetischen Oberflächenladungen zumindest in der Mitte des Streifens vernachlässigt werden. Das
interne Magnetfeld ist dabei über die Streifenbreite w nahezu konstant und entspricht dem extern
angelegten Magnetfeld. Abbildung 2.4 aus Ref. [28] zeigt nun das Spinwellenspektrum einer solchen Quantisierung, wobei die gemessenen Wellenvektoren parallel zur z-Achse liegen, so dass
es sich um magnetostatische Oberflächen“-Moden handelt. Dabei wurde ein äußeres Magnetfeld
”
15
2.2 Spinwellen
von 500 Oe angelegt. Die Ränder des Streifens in z-Richtung bilden dabei Umkehrpunkte für die
Spinwellen , so dass sich über die Streifenbreite stehende Spinwellen ausbilden.
Abbildung 2.4:
Spinwellenspektrum eines entlang der langen Achse magnetisierten Streifens in MSSW-Geometrie, aufgenommen mit der Brillouin-Lichtstreumikroskopie. Die Länge L beträgt 500 µm, die Breite w = 1,8 µm. Die
Wellenprofile über die Streifenbreite sind dabei den gemessenen Moden von n = 0...4 zugeordnet. Entnommen ist die Abbildung aus [28].
Dadurch kann die z-Komponente nur die diskreten Werte
kz =
nπ
w
(2.43)
annehmen. n ist dabei die Modenzahl und gibt die Anzahl der Knoten der stehenden Welle an.
Diese Lösung berücksichtigt allerdings noch nicht die Streufelder an den Seitenrändern des Streifens, die durch die dynamischen Komponenten der Magnetisierung erzeugt werden. Diese erzeugen aufgrund des Kreuzprodukts in Gleichung 2.13 ein Drehmoment, welches phänomenologisch
durch Einführung neuer Randbedingungen, die an den seitlichen Rändern wirken, berücksichtigt
wird [31]:
16
2.2 Spinwellen
∂m
1
+ m = 0;
∂y ξD
ξD =
d
w
(1 + 2 ln ),
w · 2π
d
(2.44)
wobei m die durch die Spinwellen dynamisch erzeugte Magnetisierung des Streifens ist. Das Oberflächendrehmoment wird durch den Parameter ξD berücksichtigt. Im Falle eines geringen AspektVerhältnisses p = wd , d.h d ¿ w können die Randbedingungen folgendermaßen gelöst werden [32]:
nπ
kz =
;
we f f
we f f = w(
ξD −1
ξD −1 − 2
)
(2.45)
Da die Spinwelle nun auf einen bestimmten Raumbereich lokalisiert ist, wird der Wellenvektor
gemäß der Unschärferelation
∆kz ∆z ≈ 2π
(2.46)
verwaschen“. Daher können die Frequenzen in Abbildung 2.4 nur über einen endlichen Wel”
lenvektorbereich gemessen werden. Allerdings kann man auf diese Art und Weise durch die Bestimmung des Wellenvektorbereichs, in dem eine quantisierte Spinwelle beobachtet wird, auf die
Lokalisierungslänge und damit auf die Streifenbreite Rückschlüsse ziehen.
Quantisierung durch Inhomogenitäten des internen Magnetfeldes
Neben der Begrenzung des magnetischen Volumens können auch Inhomogenitäten des internen
Magnetfeldes zur Quantisierung von Spinwellen führen. Inhomogenitäten können dabei verschiedene Ursachen haben. So kann z.B. eine Domänenwand zu einer inhomogenen Feldverteilung
des internen Feldes führen. Auch die bereits beschriebene Entmagnetisierung führt zu Inhomogenitäten des internen Magnetfeldes. Betrachtet man noch einmal einen magnetischen Streifen,
diesmal senkrecht zur langen Achse magnetisiert, so wird das interne Feld durch das Entmagnetisierungsfeld äußerst inhomogen. Abbildung 2.5 c), aus [30] entnommen, zeigt den Verlauf des
internen Feldes entlang der Streifenbreite. Das Entmagnetisierungsfeld reduziert dabei das interne
Feld in der Streifenmitte. Das Nullfeld muss dabei nicht zwangsläufig bei z = ±w/2 eintreten,
sondern kann unter Ausbildung von Randdomänen bereits vorher erreicht werden (siehe Abb. 2.5
c)). In Abbildung 2.5 b) sind die Dispersionsrelationen der MSBVW an verschiedenen Positionen
des Streifens und damit für verschiedene Magnetfelder dargestellt. Dabei werden die Dispersionsrelationen der MSBVW gemäß Gleichung 2.42 für größere Felder zu höheren Frequenzen hin
verschoben. Somit existiert für eine Spinwelle mit fester Frequenz ab einem bestimmten internen
Feld und somit für eine bestimmte Position des Streifens kein reeller Wellenvektor mehr. Diese
17
2.2 Spinwellen
Position bildet für die Spinwelle dann den Knotenpunkt. Das inhomogene Feld stellt für Spinwellen einen Potentialtopf dar, dessen Eigenzustände analog zur Quantenmechanik mit Hilfe eines
Phasenquantisierungsintegrals [30]
I
k[H(z),ν] dz = 2πr + Φ1 + Φ2
(2.47)
berechnet werden können, wobei Φ1 und Φ2 die Phasensprünge an den Knotenpunkten der stehenden Spinwellen darstellen und von der Geometrie des zu untersuchenden Objekts abhängen. Der
Wellenvektor ist dabei durch die Dispersionsrelation der MSBVW 2.42 bestimmt und r bezeichnet
die möglichen Eigenzustände des Potentialtopfs.
Frequenz [GHz]
(c)
L
(a)
(b)
k
w||z
k
5
M
k
-1
Wellenvektor [10 cm ]
Abbildung 2.5:
a) Spinwellenspektrum eines senkrecht zur langen Achse magnetisierten Streifens der Länge L = 500 µm
und Breite w = 1 µm in der MSBVW-Geometrie. Während der Messung war ein Feld von H = 500 Oe angelegt. Die Moden, die nicht mehr experimentell aufgelöst werden können, bilden das Spinwellenband. Die
senkrecht zur Schicht stehenden Spinwellen (engl.: Perpendicular Standing Spin Waves PSSW) sind durch
die Inhomogenität der Spinwelle aufgespalten.
b) Dispersionsrelation der MSBVW für verschiedene Magnetfelder. Der erlaubte Wellenvektorbereich einer
Spinwelle kann durch die Schnittpunkte von einer Linie konstanter Frequenz mit den Dispersionsrelationen
bestimmt werden. Dies wird anhand der LM(low f requency mode)-Mode aus a) exemplarisch gezeigt.
c) Profil des internen Magnetfeldes über die Streifenbreite. ∆z gibt dabei den Bereich an, in dem die LMMode lokalisiert ist. Die Abbildungen wurden aus [30] entnommen.
Die für r = 1 berechnete Eigenfrequenz von ν = 4,5 GHz stimmt dabei mit der als LM
3 low
3
be-
frequency mode
18
2.2 Spinwellen
zeichneten Mode in dem gemessenen Spinwellenspektrum aus Abbildung 2.5 a) überein und ist
in Abbildung 2.5 b) als gestrichelte Linie eingezeichnet. Es zeigt sich, dass nur für Magnetfelder
zwischen H = 0 Oe und H = 237 Oe ein Schnittpunkt mit der berechneten Dispersionsrelation existiert. Anhand von Abbildung 2.5 c) lassen sich in diesem Bereich des Feldes zwei Umkehrpunkte
der Spinwelle zuordnen, die auf dem Streifen den Bereich ∆z eingrenzen. Die im Rahmen dieses Modells gefundene Lokalisierung der Spinwelle mit einer Frequenz von ν = 4,5 GHz in dem
schmalen Bereich ∆z wird experimentell dadurch gestützt, dass in den gemessenen Spinwellenspektren die Mode LM über den gesamten messbaren Wellenvektorbereich nachgewiesen werden
konnte und somit nach Gleichung 2.46 stark lokalisiert ist. Da die höheren Eigenzustände des Potentialtopfes mit r = 2,3,... durch die begrenzte spektrale Auflösung des Experiments nicht mehr
getrennt werden können, bilden sie das Frequenzband in Abbildung 2.5 a).
19
2.3 Domänenwände in weichmagnetischen Nanostreifen
2.3. Domänenwände in weichmagnetischen Nanostreifen
Aufgrund der großen Fortschritte in der Probenpräparation im Submikrometer-Bereich in den letzten Jahren ist die Untersuchung von magnetischen Streifen auf der Nanometer-Skala immer mehr
in den Fokus gerückt. Häufig wird dabei weichmagnetisches Material verwendet, da dieses ein
niedriges Koerzitivfeld Hc besitzt und somit Domänenwände sich einfach bewegen lassen. Der
Prototyp“ eines solchen weichmagnetischen Materials ist Permalloy (Ni81 Fe19 ). Von Nanostrei”
fen spricht man, wenn die Streifendicke und die Streifenbreite im Nanometerbereich liegen und
der Streifen ein sehr kleines Aspekt-Verhältnis aufweist, d.h die Streifendicke wesentlich kleiner
als die Streifenbreite ist. Typischerweise beträgt die Dicke 1 − 20 nm und die Breite 40 nm bis
mehrere Hundert Nanometer.
Lange Zeit ging man davon aus, dass in solchen Nanostreifen nur zwei Arten von Domänenwänden
existieren, die transversale Domänenwand (TDW) und die Vortex-Domänenwand (VDW). Bei einer transversalen Domänenwand (Abb. 2.6 a)) ist die Magnetisierung in der Mitte der Wand transversal zur Streifen-Achse ausgerichtet. Bei der Vortex-Wand, wie sie in Abbildung 2.6 b) zu sehen
ist, bildet sich in der Mitte der Wand ein Wirbel, ein sogenannter Vortex aus [5], [33].
Abbildung 2.6:
Mögliche Domänenwand-Strukturen in einem weichmagnetischen Nanostreifen, der in longitudinaler Richtung magnetisiert wurde. (a) zeigt eine (symmetrische) transversale Domänenwand, bei der die Magnetisierung in der Mitte der Wand transversal zur Streifen-Achse ausgerichtet ist. Bei der Vortex-Wand in (b) bildet
sich in der Mitte der Wand ein Wirbel aus, ein sogenannter Vortex. (c) zeigt eine asymmetrische transversale
Domänenwand, deren Existenz erst später entdeckt wurde.
Ein Phasendiagramm für Ni81 Fe19 , auf mikromagnetischen Simulationen beruhend, zeigt die Abbildung 2.7 aus Ref. [34]. Dabei wird die Streifendicke doppelt logarithmisch gegen die Streifenbreite aufgetragen. Sowohl die Dicke als auch die Breite sind auf die magnetostatische Austauschlänge normiert. Der Phasenübergang von einer transversalen Domänenwand zu einer VortexDomänenwand ist erster Ordnung.
Auch experimentell wurden zu dieser Zeit nur diese beiden Typen von Domänenwänden nachgewiesen [35]. Das Problem der mikromagnetischen Simulationen war jedoch, dass die Schrittweite
der benutzten Parameter zu groß gewählt wurde, so dass eine dritte Art der Domänenwand in
Nanostreifen unentdeckt blieb, bis genauere Berechnungen auf deren Existenz hindeuteten. Diese
Domänenwand wird als asymmetrische transversale Domänenwand (aTDW) bezeichnet, siehe Abbildung 2.6 c). Betrachtet man nun das genauere Phasendiagramm für Ni81 Fe19 in Abbildung 2.8,
20
2.3 Domänenwände in weichmagnetischen Nanostreifen
Abbildung 2.7:
Phasendiagramm für Ni81 Fe19 , das nur zwei mögliche Domänenwände, die TDW und die VDW, darstellt. Die
Phase der asymmetrischen TDW ist noch nicht eingezeichnet. Bei diesem Phasendiagramm ist die Streifendicke hier tcrit genannt, doppelt logarithmisch gegen die Streifenbreite, wcrit aufgetragen. Dabei sind sowohl
die Dicke, als auch die Breite auf die magnetostatische Austauschlänge δ normiert. Das Phasendiagramm
wurde aus [34] entnommen.
entnommen aus Ref. [33], so zeigt sich, dass die aTDW nur in einem schmalen Bereich existiert,
der im vorherigen Diagramm der normalen symmetrischen TDW zugeordnet wurde. Der Übergang
von einer TDW zu einer aTDW ist dabei zweiter Ordnung, wohingegen der Phasenübergang von
einer TDW zu einer VDW weiterhin erster Ordnung bleibt. Der Nachweis der Existenz von asymmetrischen transversalen Domänenwänden erfolgte kurz Zeit später experimentell [36].
Abbildung 2.8:
Phasendiagramm für Ni81 Fe19 , bei dem nun alle drei verschiedenen Domänenwand-Typen eingezeichnet
sind [33]. Diesmal ist jedoch die Streifenbreite gegen die Streifendicke aufgetragen. Die asymmetrische
TDW existiert dabei nur in einem schmalen Band, das vorher der TDW zugeordnet wurde. Der Übergang
von einer TDW zu einer aTDW ist dabei von zweiter Ordnung, der Phasenübergang von einer TDW zu einer
VDW bleibt hingegen weiterhin erster Ordnung.
21
KAPITEL 3
Experimenteller Aufbau
3.1. Brillouin-Lichtstreuspektroskopie
3.1.1 Generelle Funktionsweise
Seit einiger Zeit wird zur Untersuchung der Magnetisierungsdynamik in magnetischen Schichtsystemen äußerst erfolgreich die Brillouin-Lichtstreuspektroskopie eingesetzt [31, 37–39]. Sie beruht
auf dem Prinzip der inelastischen Streuung von Photonen an Magnonen, den elementaren Schwingungsanregungen des Spinsystems eines Festkörpers. In Folge eines solchen Streuprozesses kann
nun entweder ein Magnon erzeugt (Stokes-Prozess) oder vernichtet (Anti-Stokes-Prozess) werden.
Anschaulich ist dies in Abbildung 3.1 gezeigt.
Abbildung 3.1:
Darstellung eines Stokes-Prozesses bzw. eines Anti-Stokes-Prozesses. Die beiden Prozesse beschreiben die
Wechselwirkung zwischen einem Photon der Frequenz ωi und einem Magnon der Frequenz ω. Als StokesProzess bezeichnet man dabei die Erzeugung eines Magnons, der Anti-Stokes-Prozess die Vernichtung.
Im Rahmen der Energie- und Impulserhaltung bei denen eine Translationsinvarianz des Raumes
und die Homogenität der Zeit vorausgesetzt werden, gelten für die Frequenz ωs und den Wellenvektor ks des gestreuten Lichts:
22
3.1 Brillouin-Lichtstreuspektroskopie
h̄ωs = h̄ωe ± h̄ω
h̄ks = h̄ke ± h̄k
Energierhaltung
(3.1)
Impulserhaltung
(3.2)
Die Frequenz und der Wellenvektor des einfallenden Photons werden in diesem Zusammenhang
mit ωi und ki bezeichnet. Frequenz und Wellenvektor des Magnons besitzen keinen Index. Anschaulich kann die Wechselwirkung von Photonen und Magnonen damit beschreiben werden, dass
die dynamischen Komponenten der Magnetisierung die Permeabilität des Festkörpers beeinflussen, was zu einer dynamischen Modulation der Polarisation führt. Diese Modulation der Polarisation wirkt dabei auf die einfallenden Photonen wie ein Phasengitter. Somit ist der Streuprozess
klassisch eine Bragg-Reflexion des Lichtes an einem sich bewegenden Phasengitter. Die Frequenz
des Lichtes ist dabei durch den Doppler-Effekt verschoben:
ωs = ωi − k · v
(3.3)
Somit ist v gerade die Propagationsgeschwindigkeit der Spinwelle im Medium:
v = (ω/k2 ) · k.
(3.4)
G = k = ki − ks
(3.5)
Über die Bragg-Bedingung
erhält man wieder die Gleichungen 3.1 und 3.2. Da die Spinwelle das Gitter erzeugt, entspricht der
reziproke Gittervektor G gerade dem Wellenvektor.
Die Energie eines Magnons kann nun als Funktion der Frequenzverschiebung des gestreuten Lichts
gemessen werden. Dieses ist möglich, da nach wie vor die Energieerhaltung gilt. Nach 3.5 kann
der maximal übertragende Wellenvektor dem doppelten Wellenvektor des einfallenden Photons
entsprechen. Die Phasengeschwindigkeit von Magnonen ist im Vergleich zur Lichtgeschwindigkeit sehr klein, so dass die zu messenden Frequenzunterschiede bei gleichem Wellenvektor von
Licht und Magnon sehr klein sind und typischerweise im GHz-Bereich liegen. Die Ansprüche der
Brillouin-Lichtstreuspektroskopie an die Lichtquelle und an das zur Energiemessung verwendete Interferometer sind dementsprechend hoch. Aus diesem Grund wird ein frequenzstabilisierter
Festkörper-Laser sowie ein Tandem-Fabry-Perot Interferometer [37], [40] verwendet, deren Merkmale ausführlich in Ref. [27] erläutert sind.
Als zweite Messgröße ist neben der Frequenz der Spinwellen auch der Wellenvektor selber als
23
3.1 Brillouin-Lichtstreuspektroskopie
Messgröße zugänglich. Die Translationssymmetrie senkrecht zur Filmebene ist bei der Streuung
an dünnen Filmen gebrochen. Daher gilt für die Komponente des Wellenvektors senkrecht zum
Film die Impulserhaltung 3.2 nicht mehr. Allerdings ist sie für die in der Schichtebene liegende
Komponente kk des Wellenvektors weiterhin erfüllt. Wenn nur Licht in das Interferometer gelangt,
das parallel oder antiparallel zur Einfallsrichtung gestreut wird, kann die gemessene Frequenz eindeutig einem Wellenvektor zugeordnet werden. Dieser Wellenvektor kann schließlich über den
Winkel zwischen einfallendem Lichtstrahl und Probenebene berechnet werden:
kk = ki sin θ =
2π
λLaser
sin θ.
(3.6)
Abbildung 3.2:
Darstellung der zwei üblichen Streugeometrien der Brillouin-Lichtstreumikroskopie. (a) zeigt die Streuung
in Vorwärtsrichtung und (b) die Streuung in Rückwärtsrichtung.
Wird in Rückwärtsrichtung gestreut, wie in Abbildung 3.2 b) gezeigt, so wird bei maximal streifendem Einfall der doppelte Impuls des einfallenden Lichts übertragen. Bei Streuung in Vorwärtsrichtung (Abbildung 3.2) hingegen kann maximal der Wellenvektor des einfallenden Lichts übertragen
werden.
Abbildung 3.3 a) zeigt nun die experimentelle Realisierung der Streuung in Vorwärtsrichtung. Verwendung findet diese Konfiguration bei transparenten Proben, allen voran Yttrium-Eisen-Granat
(YIG). Der Lichtstrahl wird dabei durch zwei Umlenkprismen auf die Rückseite der Probe fokussiert. Dabei wird das inelastisch gestreute Licht mit Hilfe eines Kameraobjektivs kollimiert und
danach wieder in das Interferometer eingekoppelt.
Bei der Streuung in Rückwärtsrichtung, die in dieser Arbeit verwendet wurde, wird der Laserstrahl
über einen kleinen Spiegel in ein Kameraobjektiv geführt, welches den Strahl dann auf die Probe
bündelt. Dabei wird das an den Magnonen inelastisch gestreute Licht von demselben Objektiv immer wieder aufgesammelt und kollimiert. Mit dieser Methode können nun auch nicht-transparente
Proben untersucht und Wellenvektoren bis 2kLaser übertragen werden. Allerdings liegt der kleine
Umlenkspiegel genau auf der optischen Achse, so dass ein Teil des inelastisch gestreuten Lichts
ausgeblendet wird.
24
3.1 Brillouin-Lichtstreuspektroskopie
Abbildung 3.3:
Experimentelle Realisierung der Vorwärtsstreuung (a) und der Rückwärtsstreuung (b), entnommen aus [27].
3.1.2 Brillouin-Lichtstreumikroskopie
Bei der eben vorgestellten Messgeometrie in Rückwärtsstreuung wird zur Fokussierung des Laserstrahls ein Kameraobjektiv mit einer langen Brennweite verwendet. Das von den Magnonen dabei
inelastisch gestreute Licht wird nur in einem kleinen Raumwinkel in der Umgebung des einfallenden Lichtstrahls aufgesammelt. Dieses bestimmt zum größten Teil die Auflösung des Experiments
bezüglich des Wellenvektors [41]. Die Ortsauflösung verschlechtert sich in zunehmendem Maße
mit Erhöhung der Brennweite des Objektivs, da der Durchmesser des fokussierten Laserstrahls
in der Probenebene größer wird. Typischerweise wird daher nur ein minimaler Strahldurchmesser
von 30-50 µm auf der Probe erreicht [28]. Bei der Untersuchung der Magnetisierungsdynamik ist
man bei magnetischen Strukturen auf der Mikrometer- oder Nanometer-Skala auf Gitter mit sehr
vielen identischen Strukturen begrenzt [28–30,42]. Dabei müssen die magnetischen Elemente weit
genug voneinander entfernt sein, um dipolare Kopplungen der einzelnen Elemente untereinander
zu vermeiden, andererseits müssen die Strukturen so dicht gepackt sein, dass das Streuvolumen
ausreichend groß ist. Bei der Auswahl der zu untersuchenden Elemente ist man deshalb erheblich
eingeschränkt. Es ist notwendig, den Laserstrahl auf ein Streuvolumen von unter einem Mikrometer Kantenlänge zu fokussieren. Der Durchmesser w des fokussierten Strahls, das sogenannte
Airy-Scheibchen, lässt sich folgendermaßen mit dem Durchmesser des unfokussierten Strahls W0
und der Brennweite f des verwendeten Objektivs verknüpfen [43]:
w ≈ 1,22 ·
f ·λ
.
W0
(3.7)
Folglich muss der Strahldurchmesser W0 vergrößert und die Brennweite des Objektivs f verkleinert
werden, um eine höhere räumliche Auflösung zu erreichen. Dieses führt dazu, dass der fokussierte
Laserstrahl nun einen großen Raumwinkel mit dem Öffnungswinkel β = arcsin(NA) ausfüllt. Die-
25
3.1 Brillouin-Lichtstreuspektroskopie
ses ist in Abbildung 3.4 verdeutlicht. Der dabei durch die Teilstrahlen kmin und kmax übertragene
Wellenvektorbereich ist dabei umso größer, je größer der Öffnungswinkel β ist.
Abbildung 3.4:
Der Durchmesser w des zentralen Maximums, das sogenannte Airy-Scheibchen wird durch den Strahldurchmesser W0 und die Brennweite f des Objektivs bestimmt. Dabei ist der durch die Teilstrahlen kmin und kmax
übertragene Wellenvektorbereich umso größer, je größer der Öffnungswinkel β des Strahlkegels ist.
Die in Kapitel 3.1.1 beschriebene Wellenvektorselektivität geht dabei allerdings verloren. NA
ist die verwendete numerische Apertur des Objektivs, sie beträgt 0,75 bei dem derzeit in dem
Brillouin-Lichtstreumikroskop verwendeten Mikroskop-Objektiv. Mit Hilfe von Gleichung 3.6
und der Wellenlänge λ = 514 nm des verwendeten Festkörperlasers kann man den Wellenvektorbereich berechnen, der von dem Objektiv überhaupt erfasst werden kann. Die Wellenvektorselektivität ist bei der Brillouin-Lichtstreumikroskopie nicht von großer Bedeutung, da bei strukturierten Proben die Translationsinvarianz in der Probenebene verloren geht und dadurch der Wellenvektor von quantisierten Spinwellen bei zunehmender Lokalisierung zunehmend unschärfer
wird [28, 30, 42, 44]. Die Aufgabe der Wellenvektorselektivität ist daher ein akzeptabler Kompromiss für die wesentlich bessere Ortsauflösung.
Abbildung 3.5 zeigt den schematischen Aufbau des Brillouin-Lichtstreumikroskops. Das integrierte Beobachtungssystem wird dabei durch den gelb-grün schraffierten Teil des Strahlengangs dargestellt. Direkt nach dem Festkörperlaser wird ein Teil des Laserstrahls als Referenzstrahl für
das Interferometer ausgekoppelt. Danach wird der Strahl durch ein Teleskop aufgeweitet, um die
erforderliche Parallelität zu gewährleisten. Vor dem Objektiv befinden sich zwei polarisierende
Strahlteilerwürfel, wobei der erste der Erhöhung des Polarisationsgrads dient. Der zweite sorgt
für die Einkopplung des Lichtstrahls in das Objektiv. Zusätzlich wird durch den zweiten Strahlteilerwürfel noch der Effekt ausgenutzt, dass sich die Polarisationsebene des linear polarisierten
Lichts bei der Streuung an Magnonen um 90◦ dreht. Somit wird das inelastisch gestreute Licht von
dem unelastisch gestreuten Licht, dessen Polarisationsebene sich nicht ändert, getrennt. Das inelas26
3.1 Brillouin-Lichtstreuspektroskopie
tisch gestreute Licht wird anschließend durch ein zweites Teleskop aufgeweitet und in das Tandem
Fabry-Perot-Interferometer eingekoppelt. Nach dem Interferometer trifft das Licht schließlich auf
einen Photodetektor. Da der Fokus dieser Diplomarbeit jedoch nicht darin lag, Verbesserungen
oder Modifikationen des bestehenden Messaufbaus durchzuführen, wird an dieser Stelle auf eine
detaillierte Erklärung des Tandem Fabry-Perot-Interferometers und seiner Funktionsweise verzichtet und auf eine ausführliche Erklärung an anderer Stelle verwiesen [27].
Abbildung 3.5:
Schematischer Strahlengang durch das Brillouin-Lichtstreumikroskop. Der gelb-grün schraffierte Teil des
Strahlengangs stellt dabei das integrierte Beobachtungssystem dar. Die Probe ist dabei auf einen in alle
drei Raumrichtungen verschiebbaren Tisch zwischen zwei Elektromagneten positioniert. Die Abbildung ist
aus [27] entnommen.
27
3.2 Lorentzmikroskopie
3.2. Lorentzmikroskopie
Eine etablierte Methode magnetische Domänen und Domänenwände im Nanometerbereich zu beobachten und zu untersuchen ist die Lorentzmikroskopie [45], [46]. Sie ist eine Art der Transmissionselektronenmikroskopie und wird auch in einem modifizierten Transmissionenelektroskop
durchgeführt. Die Elektronen werden dabei typischerweise auf etwa 100 keV beschleunigt. Diese
Elektronen haben sowohl Teilchen- als auch Wellen-Charakter. Ihre Wellenlänge beträgt 0,0388
Å. Die Wechselwirkung von Elektronen und der magnetischen Induktion kann in beiden Bildern
erklärt werden. Im Teilchen-Bild werden die Elektronen durch die Lorentz-Kraft abgelenkt [47]:
FL = qe (
ve
× B),
c
(3.8)
wobei qe die Ladung und ve die Geschwindigkeit des Elektrons sind, c ist die Lichtgeschwindigkeit und B ist die magnetische Flussdichte. Dabei sind nur die Komponenten von B, die senkrecht
zum Elektronenstrahl liegen, von Bedeutung. Die Lorentz-Kraft muss über den gesamten Weg der
Elektronen integriert werden, nicht nur über den Teil der Trajektorie, der durch die Probe führt. Somit tragen Streufelder außerhalb der Probe genauso zum Kontrast bei. Im schlimmsten Fall können
diese Streufelder sogar den gesamten magnetischen Kontrast überlagern [47].
Im Folgenden werden nun die zwei gebräuchlichsten Arten der Lorentzmikroskopie , die auch im
Rahmen dieser Diplomarbeit Verwendung finden, vorgestellt.
Im sogenannten Fresnel-Modus wird der Elektronenstrahl nicht fokussiert, damit möglichst parallele Elektronenstrahlen auf die Probe treffen [45], [46]. Dabei ist eine Auflösung bis zu 30
nm erreichbar. Wie in Abbildung 3.6, entnommen aus Ref. [48], zu sehen ist, werden nun die
Elektronen, je nachdem in welchen magnetisch orientierten Bereich sie auftreffen, unterschiedlich abgelenkt. Dadurch gibt es Bereiche des Detektors, auf die vermehrt Elektronen auftreffen,
und Bereiche, auf die durch die Ablenkung keine Elektronen mehr auftreffen. Somit entsteht ein
Fresnel-Intensitätsprofil, das den magnetischen Kontrast der Probe darstellt. Der Ablenkwinkel der
Elektronen ist dabei proportional zur Komponente von B, die senkrecht zum Elektronenstrahl ist,
und zur Dicke der Probe. Bei der Lorentzmikroskopie ist man allerdings auf dünne magnetische
Schichten bis maximal 100 nm beschränkt, die zudem noch auf spezielle Substrate [49] präpariert
werden müssen, um Elektronentransparenz gewährleisten zu können. Die Substrate werden eingehend in Kapitel 4.1 beschrieben.
Bei höher aufgelösten Untersuchungen von magnetischen Strukturen wird auf eine Methode zurückgegriffen, bei der der Elektronenstrahl fokussiert wird. Die am häufigsten verwendete Methode
ist die Differential-Phasenkontrast-Methode (DPC-Methode)1 [46], [48]. Herkömmliche Objektiv1 engl.:
Differential Phase Contrast
28
3.2 Lorentzmikroskopie
Abbildung 3.6:
Die Abbildung zeigt die Ablenkung der Elektronen beim Durchgang durch eine Probe mit magnetischen
Domänen. Die Elektronen werden dabei aufgrund der Lorentz-Kraft abgelenkt. Dadurch entsteht am Detektor ein Intensitätsprofil durch das sich Rückschlüsse auf die magnetischen Domänen ziehen lassen. Der
Ablenkwinkel der Elektronen wird mit βL bezeichnet. Die Abbildung wurde aus Ref. [48] entnommen.
Linsen eines Transmissionselektronenmikroskops sind allerdings ungeeignet, da diese ein starkes Feld senkrecht zur Probe aufbauen und folglich Untersuchungen an magnetischen Schichten
unmöglich werden. Aus diesem Grund wurden spezielle Lorentz-Linsen entwickelt [46], die erheblich kleiner als herkömmliche Linsen sind und deren Feld nicht bis zur Probe selber reicht. Wie
in Abbildung 3.7 zu sehen ist, befindet sich ein Satz Lorentz-Linsen vor der Probe und ein Satz
hinter der Probe.
Die DPC-Methode beruht auf dem sogenannten Aharonov-Bohm Effekt [50]. Zwei Elektronenstrahlen erleiden durch magnetische Induktion einen Phasensprung, wenn sie von einem gemeinsamen Ursprung aus starten, zwei unterschiedliche Wege durch einen magnetischen Fluss gehen
und sich schließlich wieder vereinigen. Die magnetische Probe wirkt also wie eine Art ”Phasenobjekt”für den Elektronenstrahl. Daher ist die Lorentzmikroskopie immer eine Messmethode, bei der
der Phasenkontrast aufgenommen wird. Bei der DPC-Methode wird dieser Phasenkontrast durch
einen Detektor aufgenommen, der in vier Quadranten unterteilt ist. Die Differenzsignale der jeweils gegenüberliegenden Detektoren liefern Bilder der zwei orthogonalen Komponenten der magnetischen Induktion der Magnetisierung. Abbildung 3.8 a) und b), entnommen aus Ref. [48], zeigen diese orthogonalen Komponenten einer 1 µm x 200 nm großen Probe aus Ni81 Fe19 . Abbildung
29
3.2 Lorentzmikroskopie
Abbildung 3.7:
Schematischer Strahlengang der Elektronen bei der DPC-Methode aus Ref. [48]. Dabei handelt es sich
anders als bei der Fresnel-Methode um eine In-Fokus-Technik. Zwei Elektronenstrahlen, die von einem
gemeinsamen Punkt aus auf zwei Wegen durch die Probe wandern, haben nach der Refokussierung einen
Phasenunterschied. Dieser Phasenunterschied wird auf einem Detektor, der in vier Quadranten unterteilt
wird, detektiert. Die Differenzsignale der jeweils gegenüberliegenden Detektoren liefern somit Bilder der
zwei orthogonalen Komponenten der magnetischen Induktion der Magnetisierung.
3.8 c) zeigt eine schematische Darstellung der Domänenstruktur der Probe und d) eine HellfeldTransmissionselektronenmikroskop-Aufnahme des Ni81 Fe19 -Elements. Die Auflösung der DPCMethode liegt bei 2 nm bis 20 nm. Es können magnetische Strukturen in Remanenz oder bei angelegtem Feld über einen weiten Temperaturbereich untersucht werden. Durch die Informationen,
die man durch die DPC-Methode gewinnen kann, lassen sich Rückschlüsse auf die mikromagnetischen Eigenschaften, die Domänenwandstrukturen und evtl. vorhandene ”Pinning-Center”(genaue
Erklärung folgt in Kapitel 5) ziehen. Ein Nachteil der Methode ist jedoch, dass die Phasensprünge
sowohl magnetostatischen als auch elektrostatischen Ursprungs sein können, wobei es zu erheblichen Problemen kommen kann, wenn letzterer überwiegt. Auch kann man keine Informationen
30
3.2 Lorentzmikroskopie
über die Komponenten der Induktion gewinnen, die parallel zur Strahlrichtung der Elektronen liegen. Die Zeitauflösung ist zudem mit typischerweise einer Sekunde recht schlecht. Allerdings gibt
es keine andere Messmethode, die diese Grenzen überwindet und gleichzeitig die Vorzüge der
Lorentzmikroskopie bietet. Die in dieser Arbeit vorgestellten Untersuchungen wurden in Zusammenarbeit mit der Gruppe von John N. Chapman an der Universität Glasgow durchgeführt.
Abbildung 3.8:
(a) und (b) zeigen die orthogonalen Komponenten der magnetischen Induktion der Magnetisierung einer 1
µm x 200 nm großen Probe aus Ni81 Fe19 . (c) ist eine schematische Darstellung der Domänenstruktur der
Probe. d) zeigt eine Hellfeld-Transmissionselektronenmikroskop-Aufnahme der Probe. Die Bilder wurden
freundlicherweise von der Universität Glasgow zur Verfügung gestellt.
31
KAPITEL 4
Probenpräparation
Bei der Herstellung der Proben, die im Rahmen dieser Diplomarbeit untersucht wurden, ist grundsätzlich zwischen zwei verschiedenen Arten zu unterscheiden. Zum einen wurden Proben hergestellt, um mit Hilfe der Lorentzmikroskopie die statischen Eigenschaften der Magnetisierung zu
untersuchen. Zum anderen wurden Proben gefertigt, anhand derer das Spinwellenspektrum sowohl thermisch aktivierter als auch angeregter Spinwellen in den jeweiligen Strukturen mit Hilfe
der Brillouin-Lichtstreumikroskopie untersucht wurde. Beide Fälle unterscheiden sich leicht in der
Art der Präparation der zu untersuchenden Strukturen und grundlegend in der Wahl der verwendeten Substrate. Das Design der Proben ist an einen Ansatz angelehnt, bei dem eine Domänenwand,
angetrieben durch spinpolarisierten Strom, in einem Halbkreis Pendelbewegungen vollführt, äquivalent zu einem Gravitationspendel [9], [10]. Ein solcher Ansatz ist auch zur Untersuchung der
Wechselwirkung kohärenter Spinwellen mit einer Domänenwand geeignet. Zusätzlich wurde in die
Mitte des Halbkreises noch eine radiale Ausstülpung gesetzt, um dadurch eine Lokalisierung und
ein Haften“ 1 der Domänenwand zu erreichen. Dieses wurde bereits zuvor erfolgreich gezeigt [51].
”
Auf diesen Resultaten aufbauend wurden im Rahmen dieser Diplomarbeit Halbkreise mit einem
Radius R und einer Breite w hergestellt (siehe Abbildung 4.1). In der Mitte des Halbkreises befindet sich die radiale Ausstülpung mit Radius r, so dass sich an dieser Stelle eine Gesamtbreite b
ergibt. Auf Einzelheiten der Messungen wird ausführlich in Kapitel 5 eingegangen.
4.1. Herstellung der Proben für die Untersuchung im Lorentzmikroskop
Die Lorentzmikroskopie ist ein spezielle Art der Transmissionselektronenmikroskopie (siehe Kap
5.1.1 Lorentzmikroskopie), bei der elektronentransparente Substrate benötigt werden, die für diese
Technik geeignet sind. Seit einiger Zeit verwendet man für diesen Zweck Substrate, die ein sehr
dünnes Fenster aus Siliziumnitrid (Si3 N4 ) besitzen [49]. Abbildung 4.2 zeigt eine Skizze eines
solchen Si3 N4 -Fenstersubstrates. Die Substrate wurden von der Universität Glasgow im Rahmen
einer Kooperation zur Verfügung gestellt. Die Herstellung solcher Proben erfolgt dadurch, dass
1 engl.:
pinning
32
4.1 Herstellung der Proben für die Untersuchung im Lorentzmikroskop
Abbildung 4.1:
Halbkreis, an dem die Wechselwirkung von angeregten Spinwellen mit Domänenwänden untersucht werden
soll. Der Radius des Halbkreises ist mit R bezeichnet, die Breite mit w. In der Mitte befindet sich eine radiale
Ausstülpung mit Radius r, so dass sich an dieser Stelle eine Gesamtbreite von b ergibt.
man als erstes einen Standard-Silizium-Wafer mit einer 50 nm dicken Si3 N4 -Schicht überzieht.
Anschließend werden von der Rückseite mittels UV-Lithographie und der Verwendung von Kalilauge (KOH) 100 µm × 100 µm große Löcher in das Silizium bis zur Si3 N4 -Schicht geätzt.
Das Si3 N4 hingegen wird von der Kalilauge nur geringfügig angegriffen, so dass an diesen Stellen ein Si3 N4 -Fenster entsteht. Diese Fenster haben nun die Eigenschaft, dass Elektronen diese weitestgehend ungehindert passieren können. Die Substrate haben ein Gesamtmaß von 3 mm
× 3 mm, wie es für die Transmissionselektronenmikroskopie üblicherweise Verwendung findet.
Die Herstellung der später zu untersuchenden Strukturen erfolgte mittels eines Elektronenstrahl-
Abbildung 4.2:
Skizze eine Si3 N4 -Fenstersubstrates, wie es für die Lorentzmikroskopie benötigt wird. Das Silizium, das als
Trägerschicht verwendet wird, ist schwarz dargestellt, das Siliziumnitrid, aus dem die Membran gefertigt ist,
ist grau dargestellt. Die Skizze ist dabei nicht maßstabsgetreu. Links: Ansicht von oben; rechts: Querschnitt.
33
4.1 Herstellung der Proben für die Untersuchung im Lorentzmikroskop
lithographie-Prozesses im Nano+Bio Center der TU Kaiserslautern. Der erste Schritt in einem
solchen Prozess ist das Aufbringen einer elektronenstrahlempfindlichen Schicht2 . Die Sensitivität des Lackes besteht darin, dass die langkettigen Polymere durch die Elektronen in Polymere
geringeren Molekulargewichts aufgespalten werden, die daraufhin mit einem Lösungsmittel entfernt werden können [52], [53]. Die ursprünglichen Polymere werden von dem Lösungsmittel in
viel geringerem Maße angegriffen. Der hierbei verwendete Lack bestand aus einer 4-prozentigen3
Polymethylmethacrylat-Lösung (PMMA). Als Lösungsmittel wurde Ethyllactat (Milchsäureester)
benutzt. Das in diesem Zusammenhang verwendete Molekulargewicht des PMMA lag bei 950K4 .
Auf das Substrat aufgebracht wurde der Lack mittels einer Lackschleuder (Süss Delta 80™). Dabei
wurde der Lack auf die Probe aufgebracht und bei 6000 Umdrehungen pro Minute bei geschlossenem Deckel, einem sogenannten Gyrset™, für 30 Sekunden abgeschleudert. Der geschlossene
Deckel sorgt dafür, dass sich das Lösungsmittel nicht so schnell verflüchtigt. Dieses im Zusammenhang mit der hohen Drehzahl erzeugt eine homogene Lackschicht von etwa 130 nm. Bei der
Wahl des Lackes ist darauf zu achten, dass dieser ungefähr die dreifache Dicke des späteren Materials hat, aus dem die Struktur bestehen soll. Dieses ist notwendig, um die Strukturen beim weiter
unten beschriebenen lift-off-Prozess“ überhaupt freilegen zu können. Im Anschluss an das Auf”
schleudern muss der Lack bei 200◦ C für mindestens 20 Minuten ausgebacken werden. Dabei wird
das noch im Lack vorhandene Lösungsmittel weitestgehend aus dem Lack entfernt, und es kann im
späteren Verlauf keinen negativen Einfluss auf den Prozess haben. So könnte eventuell noch vorhandenes Lösungsmittel beim weiter unten beschriebenen Aufwachsen des Ni81 Fe19 in der Molekularstrahlepitaxieanlage zu erheblichen Haftproblemen des Lackes führen [52]. Nach diesem
Schritt wird die Probe mit einer Elektronenstrahllithographie-Anlage, einer e LiNE™ belichtet“.
”
Bei diesem Gerät ist eine Strukturbreite von 20 nm möglich. Nach dem Belichten“ mit Elektro”
nen wurde die Probe entwickelt. Dafür wurde eine Mischung aus Methylisobutylketon (MIBK)
und Isopropanol (IPA) im Verhältnis 1:3 verwendet. Die Entwicklungsdauer betrug 30 Sekunden,
gefolgt von 20 Sekunden in einem Stoppbad aus reinem IPA. Bei dem verwendeten Lack handelt es sich um einen Positiv-Lack, d.h. überall dort, wo Elektronen auftreffen, bleibt nach der
Entwicklung kein Lack mehr stehen. Die Idee ist nun, die gesamte Probe mit einer Schicht des
gewünschten Materials zu überziehen und anschließend mit einem geeigneten Lösungsmittel den
restlichen Lack zu entfernen, damit nur noch die geschriebene Struktur aus dem aufgewachsenen
Material übrig bleibt. Damit es nicht zu Haftungsproblemen an den Stellen kommt, bei denen der
Lack wegentwickelt wurde, ist es notwendig, in diesen Bereichen eventuell noch vorhandene Lackreste zu entfernen. Dieses geschieht in einem sogenannten Plasmaverascher. In diesem Gerät wird
2 im
Folgenden Lack genannt
3 Volumenprozent
4 950K
= 950000 u, wobei u die atomare Masseneinheit ist.
34
4.1 Herstellung der Proben für die Untersuchung im Lorentzmikroskop
für etwa eine Minute ein Sauerstoffplasma gezündet und somit noch vorhandene Lackreste aus den
strukturierten Bereichen der Probe entfernt. Zwar greift das Sauerstoffplasma unweigerlich auch
den noch benötigten Lack außerhalb der entwickelten Strukturen an, aber nicht in dem Maße, dass
der weitere Prozess gefährdet wäre.
Als nächster Schritt erfolgt das Aufwachsen einer 10 nm dicken Permalloy (Ni81 Fe19 )-Schicht auf
die Probe. Diese Schicht wurde in einer Molekularstrahlepitaxieanlage (MBE) auf die Probe aufgewachsen5 . Nach dem Aufwachsen der Schicht wurde ein sogenannter lift-off-Prozess durchgeführt.
Die ganze Probe wird in Aceton gelegt, damit der restliche Lack samt der sich darauf befindenden Ni81 Fe19 -Schicht gelöst wird. Was dabei übrig bleibt, ist allein die Struktur aus Ni81 Fe19 in
den Bereichen der Probe, in denen sich kein Lack vor dem Aufwachsen mehr befand, so dass das
Ni81 Fe19 direkten Kontakt mit dem Substrat hat. Abbildung 4.3 zeigt noch einmal schematisch die
Abfolge des Prozesses.
Abbildung 4.3:
Schematische Abfolge des Prozesses. Zuerst wird der Lack durch Elektronen belichtet“ und anschließend
”
entwickelt. Danach wird das gewünschte Material, in diesem Fall Ni81 Fe19 , aufgewachsen. Nach dem lift”
off“ bleibt nur noch Ni81 Fe19 an den Stellen übrig, an denen nach der Entwicklung kein Lack mehr vorhanden war.
Die prozessierten Strukturen sind konzentrische Halbkreise mit einer Breite w von 500 nm und
Radien R von 5 µm bis 50 µm in Schritten von 5 µm. Die Dicke t der Ni81 Fe19 -Halbkreise beträgt 10 nm. Abbildung 4.4 a) zeigt eine Rasterelektronenmikroskop- und b) eine Lichtmikroskopaufnahme der Halbkreisstrukturen. In der Mitte der Halbkreise befindet sich jeweils eine radiale
Ausstülpung mit einem Radius r = 250 nm, deren Zentrum gerade an der inneren Kante des halbkreisförmigen Streifens liegt. Die Ausstülpung ist in dem kleinen Ausschnitt von Abbildung 4.4a)
zu erkennen. Das Feld von Rechtecken, welches auf den Aufnahmen ebenfalls zu sehen ist, wird
für Dosistests im Lorentzmikroskop verwendet und hat keinerlei Bedeutung für die Probe an sich
oder deren Verwendung. Abbildung 4.4 b) zeigt zusätzlich das 100 µm × 100 µm große Si3 N4 Fenster des Substrates für die Lorentzmikroskopie.
5 Das
Probenwachstum in der Molekularstrahlepitaxieanlage wurde von Andreas Beck durchgeführt.
35
4.2 Eigenschaften der Proben für die Untersuchungen im Brillouin-Lichtstreumikroskop
und deren Herstellung
Abbildung 4.4:
a) Rasterelektronenmikroskopaufnahme der Halbkreisstrukturen. Der Ausschnitt zeigt die Gegend in der
Mitte des Halbkreises, in der sich die Ausstülpung befindet. Die Rechtecke verschiedener Größen unterhalb
der Halbkreise sind ausschließlich für Dosistests und haben für die Probe selber keine Bedeutung.
b) Lichtmikroskopbild der Strukturen bei 100-facher Vergrößerung. Zur besseren Abbildung des Oberflächenprofils wurde ein Differentialinterferenzkontrast-Verfahren verwendet.
4.2. Eigenschaften der Proben für die Untersuchungen im Brillouin-Lichtstreumikroskop und deren Herstellung
Die Proben, die für die späteren Untersuchungen im Brillouin-Lichtstreumikroskop hergestellt
wurden, zeigen prinzipielle Unterschiede zu den vorher beschriebenen Proben für die Untersuchung in einem Lorentzmikroskop sowohl im Design, als auch in der Wahl der verwendeten Materialien.
Zum einen werden keine Membranfenster mehr gebraucht, da im Brillouin-Lichtstreumikroskop
keine transparenten Proben benötigt werden. Somit besteht bei der Wahl des Substrates in dieser
Hinsicht keine Einschränkung. Zum anderen wurde dieses Mal ein mehrstufiger Elektronenstrahllithographie-Prozess verwendet. Somit bestand die Möglichkeit, zusätzlich eine Mikrowellenantenne an geeigneter Stelle über der Struktur zu platzieren. Mit einer solchen Antenne ist es möglich
Spinwellen anzuregen, die zeitlich und räumlich kohärent sind [54]. Dieses ist notwendig, da man
in den späteren Messungen mit dem Brillouin-Lichtstreumikroskop zwar auch an dem Spektrum
thermisch aktivierter Spinwellen interessiert ist, vor allem aber untersuchen möchte, was mit Spinwellen geschieht, die eine Domänenwand passiert haben. Dabei stellt sich die Frage, inwiefern die
Spinwellen einen Phasensprung und eine Veränderung ihrer Amplitude erfahren haben. Für diese
36
4.2 Eigenschaften der Proben für die Untersuchungen im Brillouin-Lichtstreumikroskop
und deren Herstellung
Untersuchungen benötigt man jedoch kohärente Spinwellen, die durch eine Mikrowellenantenne
angeregt werden können.
4.2.1 Eigenschaften der Proben
Insgesamt wurden zwei sich voneinander unterscheidende Probenserien für die Untersuchungen
im Brillouin-Lichtstreumikroskop hergestellt. Das Design einer Probe der ersten Serie ist in Abbildung 4.5 zu sehen. Bei den Strukturen, an denen später die Untersuchungen des Spinwellen-
Abbildung 4.5:
Strukturskizze einer Probe der ersten Serie. Die linke Abbildung zeigt die gesamte Probe mit den konzentrischen Ni81 Fe19 -Halbkreisen, wie sie schon für die Lorentzmikroskopie hergestellt wurden und der AuAntenne. In der Mitte ist ein vergrößerter Ausschnitt des Bereichs, in dem sich die Ni81 Fe19 -Halbkreise
befinden, dargestellt. Die Au-Antenne liegt in einem Winkel von 45 Grad über der Struktur. Die Abbildungen
auf der rechten Seite zeigen noch einmal den Bereich der Ausstülpung und das Ende der Au-Antenne, das
kurzgeschlossen ist.
spektrums mit Hilfe des Brillouin-Lichtstreumikroskops durchgeführt werden sollten, handelt es
sich um exakt die gleiche Serie von konzentrisch angeordneten Halbkreisen aus Ni81 Fe19 , wie
schon bei den Proben für die Lorentzmikroskopie. Auch befinden sich wieder Ausstülpungen an
den gleichen Positionen, wie bei den zuvor beschriebenen Proben. Als Antenne wurde ein koplanarer Wellenleiter benutzt. An der einen Seite war die Antenne so konzipiert, dass sie mit einer
Picoprobe™ kontaktiert werden konnte. Auf der anderen Seite wurde die Antenne gemäß Abbildung 4.5 kurzgeschlossen. Dieses Konzept der Mikrowellenantenne wurde bereits an anderer
37
4.2 Eigenschaften der Proben für die Untersuchungen im Brillouin-Lichtstreumikroskop
und deren Herstellung
Stelle ausführlich beschrieben und die Funktionalität der Antenne für solche Anwendungen getestet [54]. Im Bereich der Halbkreisstrukturen wurde der Abstand zwischen den Leitern und die Dicke der Leiter so gewählt, dass die Impedanz der Mikrowellenantenne bei 50 Ω lag. Damit soll die
Impedanzanpassung an gebräuchliche Mikrowellenbauteile, wie der Mikrowellengenerator oder
auch das Mikrowellenkabel, die ebenfalls eine Impedanz von 50 Ω aufweisen, gewährleistet sein.
Dieses ist notwendig, um Rückreflexionen an den Verbindungsstellen zu minimieren. Für einen
koplanaren Wellenleiter kann die Impedanz mit Hilfe elliptischer Integrale berechnet werden [55].
In dem hier vorliegenden Fall muss bei einer gewünschten Impedanz von 50 Ω die Breite der Leiter
2 µm betragen, der Abstand der Leiter 1,5 µm. Die Dielektrizitätskonstante von Silizium wurde dabei als ε = 11,7 angenommen. Die Strecke von der Seite, an der mit einer Picoprobe™ kontaktiert
wird, bis zu dem Bereich in dem die Halbkreisstrukturen liegen, wurde ebenfalls nach der selben
Gleichung impedanzangepasst. Dabei bleibt ein Verhältnis von Leiterbreite zu Leiterabstand von
4:3 wie schon bei der ersten Impedanzanpassung erhalten. Die Antenne liegt in einem Winkel von
45◦ über den Ni81 Fe19 -Halbkreisen, wie Abbildung 4.5 zeigt. Die Ausstülpungen in der Mitte der
Halbkreise bleiben dabei frei, da an diesen später Untersuchungen durchgeführt werden sollen.
Als Antennenmaterial wurde Gold verwendet, da es eine hohe Korrosionsbeständigkeit aufweist.
Die Antenne hat dabei eine Dicke von 150 nm. Das Substrat, auf dem die Ni81 Fe19 -Halbkreise und
die Au-Antenne aufgebracht wurden, bestand aus 500 µm Silizium mit einer Schicht von 100 nm
thermisch oxidierten SiO2 .
Bei den späteren Messungen stellte sich allerdings heraus, dass es mit den so konzipierten Antennen trotz ausführlicher Fehlersuche nicht gelang, Spinwellen anzuregen. Wahrscheinlich war die
Kontaktierung der Picoprobe™ mit der Antenne an einer Stelle schadhaft. Da die Antenne nicht
an beiden Enden kontaktierbar war, sondern an einer Stelle einen Kurzschluss hatte, ist es nicht
möglich gewesen, mit einem Vektor-Netzwerkanalysator diesen Fehler zu analysieren und zu beheben. Daher wurde mit den Proben der ersten Serie in den späteren Messungen nur das Spektrum
thermisch aktivierter Spinwellen untersucht.
Für die Messungen angeregter Spinwellen wurde eine zweite Serie von Proben hergestellt, die
einige Neuerungen aufwies. Als Substrat wurde jetzt 500 µm Silizium verwendet, auf das durch
thermisches Oxidieren eine Ein-Mikrometer dicke SiO2 -Schicht aufgebracht wurde. Es hat sich
herausgestellt, dass dieses Zweilagensystem für Anwendungen in der Mikrowellentechnik gut geeignet ist [56]. Eine weitere Modifikation betraf die Antenne selber. Die Antenne ist in Abbildung
4.6 dargestellt. Sie wurde jetzt nicht mehr kurzgeschlossen, sondern hatte zwei Anschlüsse, so
dass gegebenenfalls mit einem Netzwerkanalysator die Antenne in Transmission untersucht werden konnte. Während der eigentlichen Messung konnte die Antenne dann mit einem auf 50 Ω
impedanzangepassten Endstück kurzgeschlossen werden. Der Anfang und das Ende der Antenne
bestanden wieder aus koplanaren Wellenleitern, die mit Picoprobes™ kontaktiert werden konnten.
38
4.2 Eigenschaften der Proben für die Untersuchungen im Brillouin-Lichtstreumikroskop
und deren Herstellung
Abbildung 4.6: Strukturskizze einer Probe, bei der im Vergleich zur vorherigen Probe zahlreiche Verbesserungen vorgenommen wurden. So kann man erkennen, dass die Au-Antenne an beiden Enden kontaktierbar
ist. Dies ermöglicht eine Vermessung der Antenne in Transmission mit Hilfe eines Netzwerkanalysators und
ein eventuelle Fehleranalyse. Bei den Ni81 Fe19 -Halbkreisen wurden nur noch die drei mit den kleinsten Radien verwendet. Allerdings wurden jetzt die Breite des Halbkreises variiert, und inwieweit die Ausstülpung
aus dem jeweiligen Halbkreis herausragt. Zusätzlich wurden zwei Sätze gewöhnlicher Ni81 Fe19 -Streifen hinzugefügt, bei denen ebenfalls diese beiden Parameter verändert wurden.
In der Mitte wurde bewusst auf einer Strecke von 500 µm auf die beiden äußeren Leiter verzichtet. Ein Vorteil liegt darin, dass durch das entsprechend schmalere Design die Antenne näher an
den Bereich der Ausstülpung gelegt werden kann. Wichtiger ist jedoch, dass bei einem Streifenleiter eine größere Bandbreite von Wellenvektoren angeregt werden kann [54]. Die Antenne an sich
bestand weiterhin aus Gold und auch die Dicke blieb mit 150 nm dieselbe. Ein weiterer Unterschied zwischen den beiden Probenserien bestand darin, dass statt den zehn vorher verwendeten
Ni81 Fe19 -Halbkreisen nur noch die ersten drei mit den Radien R 5 µm, 10 µm und 15 µm verwendet wurden. Allerdings wurde nun die Breite der Halbkreise variiert. Es wurden dabei die Breiten
w 300 nm, 400 nm und 500 nm genommen. Der Radius r der Ausstülpung blieb allerdings mit
250 nm gleich. Auch wurden Halbkreise mit einer Breite von 500 nm hergestellt, bei denen eine
Ausstülpung gänzlich fehlte. Zusätzlich wurden noch weitere Halbkreise konzipiert, bei denen die
Ausstülpung nicht mehr die ganzen 250 nm aus dem jeweiligen Halbkreis herausragte, sondern nur
39
4.2 Eigenschaften der Proben für die Untersuchungen im Brillouin-Lichtstreumikroskop
und deren Herstellung
noch 200 nm bzw. 150 nm. Zu den Ni81 Fe19 -Halbkreisen wurden noch zwei Sätze gewöhnlicher
Streifen aus Ni81 Fe19 hinzugefügt, wie Abbildung 4.6 zeigt. Bei dem ersten Satz wurde die Streifenbreite w von 300 nm bis 500 nm variiert, die Ausstülpung ragte jeweils um 250 nm heraus. Beim
zweiten Satz wurde hingegen die Streifenbreite von 500 nm konstant gehalten, allerdings ragte die
Ausstülpung nur noch 100 nm, 150 nm und 200 nm aus dem Streifen heraus. Auch wurde die Antenne jetzt nicht mehr in einem Winkel von 45◦ über die zu untersuchenden Strukturen gelegt,
sondern, wie Abb. 4.6 zeigt, diesmal wenige µm von den Ausstülpungen entfernt.
4.2.2 Herstellung der Proben
Die Proben für die Untersuchung im Brillouin-Lichtstreumikroskop wurden wie schon die Proben
zuvor mit Hilfe der Elektronenstrahllithographie in Kombination mit Molekularstrahlepitaxie und
Elektronenstrahlverdampfung prozessiert. Allerdings kam dieses Mal ein mehrstufiger Prozess zur
Anwendung, bei dem die Ni81 Fe19 -Strukturen und die Antenne nacheinander auf die Probe aufgebracht wurden. Dieser Prozess ist sowohl bei den Proben der ersten Serie, als auch bei den Proben
der zweiten Serie angewendet worden.
Der erste Schritt des Prozesses diente dazu, Markierungen für die spätere Justierung der Antenne auf den Ni81 Fe19 -Strukturen zu setzen. Für die eigentlichen Messungen sind diese nicht von
belang. Als Lack wurde wieder PMMA 4% verwendet, allerdings in zwei unterschiedlichen Molekulargewichten von 600K und 950K. Zuerst wurde PMMA 600K 4% bei 4000 Umdrehungen pro
Minute für 30 Sekunden bei geschlossenem Deckel aufgesponnen und für 20 Minuten bei 200◦ C
gebacken. Anschließend wurde PMMA 950K 4% bei 6000 Umdrehungen pro Minute für 30 Sekunden bei ebenfalls geschlossenem Deckel aufgesponnen und wieder für 20 Minuten bei 200◦ C
gebacken. Dieses zweilagige Lackschicht hat den Vorteil, dass die untere Schicht aus dem Lack mit
dem geringeren Molekulargewicht später stärker entwickelt wird als die Schicht aus dem Lack mit
höherem Molekulargewicht. Dieses führt zu einem sogenannten undercut“ der Lackstrukturen,
”
wie er in Abbildung 4.7 gezeigt wird. Man sieht deutlich, dass weniger PMMA 950K 4% wegentwickelt wurde als PMMA 600K 4%. Vor allem bei mitteldicken Strukturen erreicht man mit einer
solchen zweilagigen Lackschicht klar definierte Kanten der gewünschten Strukturen [56].
Nach dem Aufspinnen und Ausbacken des Lackes wurde dieser wieder mit Hilfe einer Elektronenstrahllithographie-Anlage belichtet“. Nach der Entwicklung der Probe in dem bereits erwähnten
”
Entwickler für 70 Sekunden und im Stoppbad für 30 Sekunden und dem anschließenden Plasmaveraschen wurde in einer Elektronenstrahlaufdampfanlage (Pfeiffer Classic 500 L) Silber in einer
Dicke von 100 nm als Material für die Markierungen aufgedampft. Bei den ersten Proben wurde
Chrom verwendet, jedoch eignet sich Silber besser, da es eine höhere Ordnungszahl und damit
verbunden einen höheren Streuquerschnitt hat. Durch die Verwendung von Silber erhöht sich deswegen der Kontrast. Danach erfolgte ein ultraschallunterstützter lift-off mit Aceton. Der zweite
40
4.2 Eigenschaften der Proben für die Untersuchungen im Brillouin-Lichtstreumikroskop
und deren Herstellung
Abbildung 4.7:
Die Abbildung zeigt den Ablauf der Strukturierung eines 2-Lagen-Lacks. Dieser 2-Lagen-Lack wurde für die
Markierungen verwendet, mit denen später die Antenne auf die Ni81 Fe19 -Strukturen justiert wurde. Zuerst
wird die zweilagige Lackschicht durch Elektronen belichtet“ und anschließend entwickelt. Danach wird auf
”
das Schichtsystem eine 100 nm dicke Schicht Silber deponiert. Nach dem lift-off“ bleibt nur noch Silber an
”
den Stellen übrig, an denen nach der Entwicklung kein Lack mehr vorhanden war.
Schritt befasst sich mit der Herstellung der Ni81 Fe19 -Strukturen der jeweiligen Proben. Dieses Mal
wurde aufgrund der späteren Strukturdicke von 10 nm Ni81 Fe19 nur eine einfache Schicht PMMA
900K 4% verwendet. Der Lack wurde auf die gleiche Weise aufgesponnen, ausgebacken und in der
Elektronenstrahllithographie-Anlage belichtet“ wie schon zuvor. Nach der Entwicklung und dem
”
Plasmaveraschen wurde eine 10 nm dicke Schicht Ni81 Fe19 in der Molekularstrahlepitaxieanlage
aufgewachsen. Der anschließende lift-off Prozess fand wieder ultraschallunterstützt statt.
Im dritten Schritt wurde die Antenne auf die entsprechenden Strukturen aufgebracht. Da die Antenne später eine Dicke von 150 nm haben sollte wurde ein dreilagiges Schichtsystem aus PMMA
950K 4% gewählt, das eine Schichtdicke von mehreren hundert Nanometern erreichen kann, so
dass der lift-off ohne weitere Probleme funktioniert. Der Lack wurde in der ersten Probenserie mit
2000 Umdrehungen pro Minute für 30 Sekunden und geschlossenem Deckel aufgesponnen und
anschließend wieder bei 200◦ C für 20 Minuten ausgebacken. Diese Prozedur ist dreimal wiederholt worden. In der zweiten Probenserie wurde die Drehzahl auf 4000 Umdrehungen pro Minute
erhöht, da dieses für die Schichtdicke ebenfalls ausreichend ist, jedoch die Schicht an den Rändern
homogener werden lässt. Die restlichen Prozessschritte wurden analog zu vorher durchgeführt, wobei nach dem Plasmaveraschen in der Elektronenstrahlaufdampfanlage 150 nm Gold aufgedampft
wurden.
Rasterelektronenmikroskopaufnahmen der Proben der beiden unterschiedlichen Serien sind in Abbildung 4.8 zu sehen. Dabei sind die jeweiligen relevanten Strukturen noch einmal in vergrößerten
Ausschnitten dargestellt.
41
4.2 Eigenschaften der Proben für die Untersuchungen im Brillouin-Lichtstreumikroskop
und deren Herstellung
Abbildung 4.8:
a) Rasterelektronenmikroskopaufnahme einer Probe der ersten Serie. Zu sehen sind die Ni81 Fe19 -Halbkreise
mit der darauf liegenden Antenne. Der Ausschnitt zeigt den Bereich der Ausstülpung in der Mitte des Halbkreises.
b) Rasterelektronenmikroskopaufnahme einer Probe der zweiten Serie. Deutlich sichtbar sind die Antenne, die Ni81 Fe19 -Strukturen sowie die Ag-Markierungen, die für die Justierung benutzt wurden. Die beiden
Ausschnitte zeigen einen Satz von Ni81 Fe19 -Halbkreise und den Bereich der Ausstülpung.
42
KAPITEL 5
Experimentelle Ergebnisse
5.1. Charakterisierung der Domänenwandstrukturen
Um später exakte und reproduzierbare Aussagen über die Wechselwirkung von kohärenten Spinwellen mit einer Domänenwand treffen zu können, ist es notwendig weitreichende Einblicke in
das Aussehen und in die Struktur von Domänenwänden zu gewinnen. Dieses gilt im besonderen
Maße für die im Rahmen dieser Arbeit verwendeten Proben und die dabei vorhandenen Domänenwände, da eine in-situ-Charakterisierung der Domänenstruktur im Brillouin-Lichtstreumikroskop
nicht möglich ist. Auch stellt sich die Frage, wie stabil diese initiierten Domänenwände bezüglich
eines externen Magnetfeldes sind. Für die Untersuchung von Domänenwänden gibt es im Allgemeinen mehrere Methoden. Eine der einfachsten Methoden, die Magnetkraftmikroskopie (engl.
MFM - Magnetic Force Microscopy), ist leider nicht oder nur sehr schwer verwendbar, da die zu
untersuchende Struktur aus Permalloy (Ni81 Fe19 ) bestand. Dieses Material zeichnet sich dadurch
aus, dass es u.a. sehr weichmagnetisch ist. Die Spitzen eines Magnetkraftmikroskops sind hingegen meist aus Kobalt und somit vergleichsweise hartmagnetisch. Die Magnetkraftmikroskopie
wird in dieser Konstellation leider zu einer invasiven Untersuchungsmethode, bei der das Streufeld der Spitze direkten Einfluss auf die Magnetisierung der Probe hätte. Zwar sind seit einiger
Zeit Untersuchungsspitzen erhältlich, die nur noch ein sehr geringes magnetisches Moment auf die
Probe ausüben, jedoch zeigte sich bei Untersuchungen mit einem MFM 1 , dass selbst diese low
”
moment tips“ bisher kein zufriedenstellendes Ergebnis brachten. Weitere Untersuchungsmethoden
sind die magneto-optische Kerr-Mikroskopie, deren Ortsauflösung für die hier untersuchten Proben
nicht ausreichend ist, die Untersuchung des magnetischen zirkularen Dichroismus mit Hilfe von
Röntgenstrahlen und die Lorentzmikroskopie. Die letzten beiden Methoden werden an Spezialanlagen durchgeführt, die in der Arbeitsgruppe Hillebrands nicht zur Verfügung stehen. Im Rahmen
dieser Diplomarbeit konnten Lorentzmikroskopie-Untersuchungen in Kooperation mit der Arbeitsgruppe von Prof. John N. Chapman an der Universität Glasgow, UK, durchgeführt werden. Einen
1 Die
Untersuchungen mit dem MFM wurden von S.J. Hermsdörfer durchgeführt
43
5.1 Charakterisierung der Domänenwandstrukturen
Überblick über die generelle Funktionsweise und die Vorteile dieser Technik gegenüber anderen
Untersuchungsmethoden liefert Kapitel 3.2.
5.1.1 Lorentz-Mikroskopie
Für die Untersuchungen der Domänenwände in den verwendeten Strukturen mittels Lorentzmikroskopie wurden die zu untersuchenden Strukturen auf für diesen Zweck konzipierte TEM-Substrate
aufgebracht. Die Herstellung dieser Proben und deren Aussehen wurden bereits detailliert in Kapitel 4.1 beschrieben. Die Untersuchungen selber wurden an der Universität Glasgow in der Gruppe
von John N. Chapman durchgeführt. Abbildung 5.1 a) zeigt noch einmal eine Rasterelektronenmikroskopaufnahme der zu untersuchenden Strukturen sowie b) eine Hellfeld-Aufnahme, die mit
Hilfe eines Transmissionselektronenmikroskops aufgenommen wurde. Man erkennt deutlich in
Abb. 5.1 a) die Halbkreise aus Ni81 Fe19 , die in Kapitel 4.1 vorgestellt wurden, sowie in b) nur
einen Ausschnitt eines solchen Halbkreises, in dem die Ausstülpung zu sehen ist. Weiterhin kann
man die polykristalline Struktur des Ni81 Fe19 -Films erkennen. In Abbildung 5.1 wird außerdem
noch ein Koordinatensystem definiert, das die Nomenklatur für die weitere Diskussion angibt: im
Folgenden wird die x-Richtung als parallele Richtung und die y-Richtung als transversale Richtung
beschrieben. Bei den Messungen wurde ein modifiziertes Philips CM 20 Transmissionselektronen-
Abbildung 5.1: a) Rasterelektronenmikroskopaufnahme der gesamten Strukturen. Das genaue Aussehen und
die Abmessungen der Strukturen sind in Kapitel 4.1 über die Probenpräparation erläutert .
b) Vergrößerte Hellfeld-Aufnahme der Ausstülpung, aufgenommen mit einem Transmissionselektronenmikroskop.
Es ist außerdem ein Koordinatensystem eingezeichnet, in dem die x-Richtung als parallele Richtung und die
y-Richtung als transversale Richtung für die spätere Verwendung festgelegt wird.
mikroskop verwendet. Für die Lorentzmikroskopie wurde es zusätzlich mit sogenannten Lorentzlinsen (siehe Kap. 3.2) ausgestattet, so dass Aufnahmen in einer feldfreien Umgebung möglich wa44
5.1 Charakterisierung der Domänenwandstrukturen
ren, während die eigentlichen Hauptlinsen ausgeschaltet waren. Aufgrund seiner hohen Auflösung
wurde der DPC ( Differential Phase Contrast“)-Modus verwendet, der im Kapitel 3.2 ausführlich
”
beschrieben wurde. Bei den Messungen wurde die Standard-Objektivlinse schwach fokussiert, d.h.
es wurde ein geringer Strom angelegt, so dass ein schwaches Magnetfeld entstand. Der Probenhalter wurde so verkippt, dass eine Komponente des Magnetfeldes in der Ebene lag, in der sich die
Strukturen befanden.
Abbildungen 5.2 a) und b) zeigen die Bx - und die By -Komponenten der Induktion, aufgenommen
im DPC-Modus an dem Halbkreis mit 5 µm Radius. Es sei an dieser Stelle darauf hingewiesen,
dass es sich hierbei um Abbildungen der magnetischen Induktion der Strukturen handelt, nicht
der Magnetisierung an sich [45]. Aus den Bx - und den By -Komponenten der Induktion lässt sich
Abbildung 5.2: a) Bx -Komponente der magnetischen Induktion. Aufgenommen ist die Struktur mit dem Radius 5 µm, die sich während der Messung im Zustand der Remanenz befand.
b) By -Komponente der magnetischen Induktion.
Beide Komponenten können zu einer vollständigen Vektorinduktionsverteilung zusammengesetzt werden,
wie sie in c) abgebildet ist. Das Farbrad gibt dabei die Richtung der magnetischen Induktion an. Die Punkte
A - C beschreiben markante Punkte der Domänenwandkonfiguration.
nun eine vollständige Vektorinduktionsverteilung zusammensetzen, wie sie in Abbildung 5.2 c)
farbkodiert zu sehen ist. Zusätzlich ist noch ein Farbrad angegeben, das angibt, in welche Richtung die magnetische Induktion zeigt. Die Struktur befand sich während der Messung im Zustand
der Remanenz. Dieses wurde dadurch erreicht, dass man ein transversales externes Magnetfeld
Htransversal mit einer Stärke von etwa 3500 Oe anlegte und dann wieder langsam auf 0 Oe reduzierte. Dabei wurde eine Domänenwand nukleiert. Die Spitze der Domänenwand scheint sich
45
5.1 Charakterisierung der Domänenwandstrukturen
nahe der rechten Seite der Ausstülpung bei Punkt A zu befinden, während unterhalb der Ausstülpung zwischen Punkt B und C eine komplexe Induktionsverteilung existiert. Somit zeigt sich
nun, dass die Ausstülpung ihren Zweck als pinning center“ wie erwartet erfüllt. Die Geometrie der
”
Domänenwand ist im Prinzip die einer asymmetrischen transversalen Domänenwand (aTDW), die
anschaulich durch zwei Domänenwände verschiedener Länge beschrieben werden kann. Asymmetrische transversale Domänenwände wurden bereits in Kapitel 2.3 vorgestellt. Ein Schema dieser
aTDW ist anhand einer mikromagnetischen Simulation [57] in Abbildung 5.3 gezeigt. Auf mikromagnetische Simulationen und das dafür verwendete Programm wird noch genauer im später
folgenden Abschnitt 5.1.3 eingegangen. Der prinzipielle Unterschied der nun vorliegenden Wand
Abbildung 5.3: Mikromagnetische Simulation der magnetischen Verteilung in dem Gebiet der Ausstülpung.
Die Struktur befindet sich dabei analog zu Abb. 5.2 im Zustand der Remanenz. Die Zeichnung unterhalb
der Simulation zeigt schematisch den Aufbau einer transversalen Domänenwand, die durch zwei einzelne
Domänenwände unterschiedlicher Länge dargestellt werden kann.
von einer reinen asymmetrischen transversalen Domänenwand liegt darin, dass sich aufgrund der
Ausstülpung ein Wirbel ausbildet. Jedoch ist dieser Wirbel nicht vollständig geschlossen (siehe
Abb. 5.3) und somit bildet sich kein Vortex aus, wie es für eine Vortex-Domänenwand der Fall
wäre.
Um nun die Stabilität der Domänenwand in der Gegend um die Ausstülpung zu testen, wurde
ein kleines Feld in negativer paralleler Richtung, -H parallel , angelegt. Ein solches Feld sollte die
Domänenwand noch mehr in das Gebiet direkt unter die Ausstülpung schieben und schließlich
aus dem Gebiet der Ausstülpung herausdrücken. Die Messergebnisse dazu fasst Abbildung 5.4 zusammen. Bei einem Feld von -7 Oe erkennt man eine geringe Verbreiterung des unteren Bereichs
der Domänenwand. Weitere Felderhöhung führt nun dazu, dass die Domänenwand, die in der Abbildung 5.4 mit AB bezeichnet wird, sich stärker ausprägt und sich das untere Ende der Wand
immer mehr von der Ausstülpung entfernt. Die Domänenwand AC hingegen verschwimmt zusehends, während der Winkel der Wand immer kleiner wird. Bei -13 Oe hat sich der Punkt B schon
einen Mikrometer von seiner ursprünglichen Position nach links verschoben und bei -15 Oe zeigt
46
5.1 Charakterisierung der Domänenwandstrukturen
Abbildung 5.4: Vektorinduktionsverteilungen der Messungen an der Struktur mit Radius 5 µm bei der Felder
in negativer paralleler Richtung angelegt wurden. Bei 0 Oe befindet sich die Spitze der Domänenwand auf
der rechten Seite der Ausstülpung an der Position A. Bei -7 Oe verbreitert sich die Domänenwand im unteren
Bereich. Weitere Erhöhung des Feldes führt nun dazu, dass die Domänenwand AB sich verbreitert und das
untere Ende dieser Wand nach links wandert, während die Domänenwand AC immer mehr verschwimmt.
Bei -13 Oe hat sich Punkt B schon 1 µm nach links verschoben und bei -15 Oe ist die Domänenwand
vollständig entfernt worden. Die Struktur ist nun vollständig in parallele Richtung magnetisiert. Lediglich
eine kleine Region unterhalb der Ausstülpung zeigt eine kleine Variation der Magnetisierung. Dieses ist
darauf zurückzuführen, dass ein Gleichgewicht zwischen der magnetostatischen und der Austauschenergie
hergestellt wurde.
sich, dass die Domänenwand vollständig entfernt ist. Die Struktur ist nun vollständig in parallele
Richtung magnetisiert bis auf die Region knapp unterhalb der Ausstülpung. Hier zeigt sich immer
noch eine signifikante Variation der Induktion. Dieses ist damit zu erklären, dass die Magnetisierung versucht, der Form der Ausstülpung zu folgen, um so die magnetostatische Energie zu Lasten
eines leichten Anstiegs der Austauschenergie zu verringern, damit schließlich ein Gleichgewicht
zwischen den beiden Energien vorherrscht.
Bei der Untersuchung des Halbkreises mit dem größten Radius von 50 µm zeigen sich vergleichbare Resultate wie zuvor. Abbildung 5.5 a) zeigt nun die Vektorinduktionsverteilung, bei der bereits
eine Domänenwand initialisiert und das Feld wieder auf 0 Oe reduziert wurde. Nunmehr jedoch
befindet sich die Spitze auf der gegenüberliegenden Seite der Ausstülpung bei Position D. Diese
Änderung der Position der Spitze resultiert wahrscheinlich aus der Tatsache, dass es eine kleine
Variation der Feldrichtung gab und ist in diesem Kontext nicht von Bedeutung. Wieder wird nun
47
5.1 Charakterisierung der Domänenwandstrukturen
ein Feld in negativer paralleler Richtung, -H parallel , angelegt. Jetzt jedoch soll die Domänenwand
nicht durch das Gebiet der Ausstülpung bewegt, sondern direkt herausgeschoben werden. Die Ergebnisse dieser Messungen sind in Abbildung 5.5 zu erkennen. Für Felder bis -4 Oe ist keine signifikante Veränderung der Domänenwandstruktur erkennbar. Bei -6 Oe jedoch hat sich die Position
und die Gesamtbreite der Domänenwand erkennbar verändert. Die Spitze der Wand wandert etwa
500 nm von der Position D nach links, während die Breite der Wand entlang der unteren Kante der
Struktur um etwa 50 Prozent zunimmt. Ein weiterer Anstieg des Feldes hat bis -10 Oe nur wenig
Auswirkung auf die Domänenwand, dann jedoch bewegt sich die Domänenwand vollständig aus
dem Bildfeld und hinterlässt eine praktisch uniform magnetisierte Struktur. Lediglich das Gebiet
direkt unterhalb der Ausstülpung zeigt die bereits zuvor beschriebene Variation der Magnetisierung.
Zusammenfassend lässt sich sagen, dass sich durch Lorentzmikroskopie die Formation einer
Abbildung 5.5:
Vektorinduktionsverteilungen der Messungen an der Struktur mit dem größten Radius (50 µm), bei der Felder in negativer paralleler Richtung angelegt wurden. Die Position der Spitze der Domänenwand ist jetzt
auf der linken Seite der Ausstülpung. Das liegt an einer leichten Verschiebung der Feldrichtung und ist nicht
auf den veränderten Radius des Halbkreises zurückzuführen. Bis -4 Oe ist keine signifikante Veränderung
der Domänenwand zu sehen. Bei 0 Oe befindet sich die Position der Domänenwandspitze bereits 500 nm
links von der ursprünglichen Position, während die Breite der Domänenwand im unteren Bereich um etwa
50 Prozent zunahm. Ein weiterer Feldanstieg zeigt bis -10 Oe fast keinen Anstieg, dann jedoch verschwindet die Domänenwand komplett aus dem Bildfeld und es bleibt eine praktisch uniform magnetisierte Probe
zurück. Jedoch weist das Gebiet direkt unter der Ausstülpung wieder die bereits beschriebene Variation der
Magnetisierung auf.
Domänenwand und der Einfluss von einem parallelen Feld H parallel auf die Wand erfolgreich beobachten lässt. Hochauflösende colour maps“ der Vektor-Induktionsverteilung in der Gegend der
”
Ausstülpung wurden aus den Bx - und den By -Komponenten der Aufnahmen im DPC-Modus er48
5.1 Charakterisierung der Domänenwandstrukturen
stellt. Im Zustand der Remanenz hat die Domänenwand die Form einer asymmetrischen transversalen Domänenwand mit einem kleinen Wirbel in der Magnetisierung in der Ausstülpung selber.
Ein Vergleich der Abbildungen 5.4 und 5.5 zeigt, dass die Struktur der Domänenwand im Zustand
der Remanenz weitestgehend unabhängig vom Radius der untersuchten Halbkreise war. Bei der detaillierten Untersuchung, wie die Domänenwand auf parallele Felder reagiert, wurden zwei Fälle
unterschieden. In einem Fall wurde das externe Feld dazu benutzt, die Wand von der Ausstülpung
wegzubewegen (siehe Abb. 5.5) und im anderen Fall wurde die Wand durch die Ausstülpung hindurch bewegt (siehe Abb. 5.4), bevor ein Zustand uniformer Magnetisierung erreicht wurde. Im
ersten Fall genügte schon ein Feld von 4 Oe, um die Spitze der Domänenwand von der Ausstülpung
wegzubewegen, obwohl ein doppelt so hohes Feld benötigt wurde, um die gesamte Wand schließlich endgültig zu bewegen. Dieses Resultat deutet auf die Eigenschaft der Ausstülpung als pinning
”
center“ hin. Im zweiten Fall waren wesentlich höhere Felder notwendig, um die Domänenwand
durch die Ausstülpung hindurchzuschieben. Das ist nicht weiter verwunderlich, da die Spitze der
Wand förmlich an dem Punkt verankert war, an dem die Ausstülpung gerade auf den Nanostreifen
trifft. Die Experimente zeigen deutlich, dass das kürzere der beiden Domänenwand-Segmente, die
die asymmetrische transversale Domänenwand bilden, nach und nach verschwindet, während das
längere Segment sich mehr und mehr vergrößert und einer 180◦ -Wand ähnelt.
Somit wurde bei den Untersuchungen mit Lorentzmikroskopie das komplexe Verhalten von Domänenwänden in Ni81 Fe19 -Halbkreisstrukturen, die mit einer Ausstülpung versehen waren, in situ
und mit großer Auflösung studiert. Eine Publikation über die gesammelten Untersuchungsergebnisse ist in Vorbereitung.
5.1.2 Parametervariation mittels mikromagnetischer Simulation
Bei den Untersuchungen des Verhaltens der Domänenwände in den halbkreisförmigen Ni81 Fe19 Nanostreifen mit Hilfe der Lorentzmikroskopie hat sich gezeigt, dass sich innerhalb dieser Strukturen keine reinen asymmetrischen Domänenwände ausbilden, sondern aufgrund der Ausstülpung
immer ein Wirbel in der Magnetisierung entsteht. Für weitergehende Untersuchungen, speziell
der Wechselwirkung zwischen kohärenten Spinwellen und der Domänenwand selber, ist es jedoch
wünschenswert, eine reine (asymmetrische) transversale Domänenwand zu initialisieren, da die
auftretenden Wechselwirkungen sich in ihr einfacher verstehen lassen. Als mögliche Parameter
kann die Position der Ausstülpung in Bezug zur Nanostreifenmitte, sowie die Breite und die Dicke
der Struktur variiert werden.
Für die folgenden mikromagnetischen Simulationen, die den Zweck verfolgten nun eine Konfiguration zu finden, in der eine reine transversale Domänenwand existiert, wurde das Programm
OOMMF verwendet [57]. Das Programm wird bereits seit längerer Zeit in der AG Hillebrands
benutzt und seine Funktionsweise in einer Arbeit der Gruppe diskutiert [58]. Als Konstante für
49
5.1 Charakterisierung der Domänenwandstrukturen
die Austausch-Steifigkeit Axc wurde 13·10−12 J/m verwendet und für die Sättigungsmagnetisierung von Ni81 Fe19 Ms ein Wert von 860·103 A/m. Simuliert wurde die Magnetisierungsverteilung,
jeweils für den Halbkreis mit dem kleinsten Radius, d.h. der innere Radius betrug 5 µm und der
äußere 5,5 µm. Die Gesamtgröße des simulierten Bereichs betrug 8,12 µm2 , d.h ausgehend von der
Position der Ausstülpung wurde jeweils 2,9 µm in positiver und in negativer paralleler Richtung
die Magnetisierungsverteilung berechnet. Es wurde weiterhin angenommen, dass die Strukturen
eine Schichtdicke von 10 nm besitzen. Eine Möglichkeit, eine reine asymmetrische transversale
Domänenwand zu nukleieren, liegt darin, die Position der Ausstülpung um die Hälfte in Richtung
des Halbkreisinneren zu verschieben. Damit ragen nur noch 125 nm der Ausstülpung aus dem
Halbkreis heraus. Das Ergebnis ist in Abbildung 5.6 b) zu sehen, während a) eine Simulation der
Magnetisierungsverteilung zeigt, in der die Ausstülpung an der ursprünglichen Position ist. Im Vergleich der beiden Magnetisierungsverteilungen erkennt man, dass der bereits im Abschnitt über die
Lorentzmikroskopie angesprochene Wirbel der Magnetisierung in der Ausstülpung sich deutlich
verringert hat, jedoch nicht ganz verschwunden ist. Eine weitere Möglichkeit, Vortex-Zustände der
Domänenwand in Ringstrukturen zu verringern bzw. vollständig zu unterbinden haben M. Laufenberg et al. gezeigt [36]. Anhand des Phasendiagramms 5.7 ist zu erkennen, dass bei bestehender
Schichtdicke eine Variation der Breite der Ringstruktur zu Vortex-Domänenwänden oder zu transversalen Domänenwänden führen kann. Ein ähnliches, auf mikromagnetischen Simulationen beruhendes, Phasendiagramm wurde bereits in Kapitel 2.2.4 vorgestellt. Bei einer Schichtdicke von
10 nm, wie in dem hier vorliegenden Fall, würde eine Verringerung der Breite zu dem gewünschten
Resultat führen. Abbildung 5.6 c) und d) zeigen die simulierten Magnetisierungsverteilungen von
den Breiten 400 nm und 300 nm der Halbkreisstruktur. Man kann in beiden Fällen erkennen, dass
noch ein Vortex-ähnlicher Wirbel direkt im Bereich der Ausstülpung vorhanden ist, sich bei einer
Breite von 300 nm fast ein vollständiger Vortex gebildet hat. Das ist damit zu erklären, dass bei den
Untersuchungen, die M. Laufenberg et al. durchgeführt haben, keine Ausstülpungen vorhanden
waren und diese einen größeren Einfluss auf die Struktur und die Gestalt der Domänenwand haben
als die Breite des eigentlichen Halbkreises. Auch die in Abbildung 5.6 e) simulierte Magnetisierungsverteilung einer Halbkreisstruktur, wie in a), jedoch mit einer Reduzierung der Schichtdicke
auf 7 nm, zeigte kein zufriedenstellendes Ergebnis.
Zusammenfassend lässt sich sagen, dass die Simulationen darauf hindeuten, dass der wesentliche
Parameter zur Optimierung der Domänenwandstruktur das Verhältnis der Streifenbreite w zur Breite an der Stelle der Ausstülpung b ist. Einen genauen Aufschluss über die Abhängigkeit des Aussehens der Domänenwand in Bezug auf die angesprochenen Maßnahmen bringen weiterführende
Untersuchungen mit Hilfe der Lorentzmikroskopie, jedoch war das im Rahmen dieser Diplomarbeit aus zeitlichen Gründen nicht mehr möglich.
50
5.1 Charakterisierung der Domänenwandstrukturen
Abbildung 5.6:
Mikromagnetische Simulationen der Magnetisierungsverteilungen der Halbkreisstruktur mit Radius 5 µm.
a) zeigt die ursprüngliche Struktur, bei der die kreisförmige Ausstülpung einen Radius von 250 nm hat und
das Zentrum der Ausstülpung gerade an der Oberkante des gebogenen Streifens ansetzt. b) zeigt nun eine
Simulation, bei der das Zentrum um 125 nm in das Innere des Streifens verschoben wurde und somit nur
noch 125 nm herausragt. Man kann erkennen, dass der Wirbel in der Magnetisierung, der durch die Ausstülpung hervorgerufen wird, sich deutlich verringert hat, jedoch nicht ganz verschwunden ist. Bei c) und d)
wurde nun der Radius und die Position der Ausstülpung unverändert gelassen, jedoch wurde die Breite des
gebogenen Streifens auf 400 nm bzw. 300 nm verringert. Man kann erkennen, dass sich der Wirbel in keiner Weise reduziert hat und dass bei einer Breite von 300 nm sich fast ein vollständig geschlossener Wirbel
ausbildet. e) zeigt die simulierte magnetische Verteilung einer Struktur mit den gleichen Abmessungen wie
in a), jedoch wurde die Schichtdicke auf 7 nm reduziert. Ein Vergleich mit a) zeigt, dass in diesem Fall kaum
Unterschiede zu erkennen sind.
51
5.2 Charakterisierung des Spinwellenspektrums
Abbildung 5.7:
Experimentell bestimmtes Phasendiagramm der verschiedenen Domänenwände in Ni81 Fe19 -Ringen bei
Raumtemperatur. Die schwarzen Quadrate geben dabei Vortex-Domänenwände und die roten Kreise transversale Domänenwände an. Die Phasengrenzen sind durch durchgezogene Linien gekennzeichnet. Das Diagramm wurde aus Ref. [36]) entnommen.
5.2. Charakterisierung des Spinwellenspektrums
Ein wichtiges Ziel des Projekts ist und war es herauszufinden, welche Auswirkungen das Passieren einer Domänenwand auf einlaufende Spinwellen hat. Dabei stellt sich die Frage, inwiefern
die Spinwellen eine Änderung der Phase und eine Modulation der Amplitude erleiden. Somit ist
es letztendlich wünschenswert, stroboskopisch Laufzeitexperimente mit Spinwellenpulsen durchzuführen und schließlich deren Veränderungen bzgl. der Phase und Amplitude zeitlich zu detektieren. Um dieses zuverlässig zu erreichen, war eine detaillierte Charakterisierung der auftretenden
Domänenwandstrukturen, wie sie in Kapitel 5.1 vorgestellt wurden, essentiell. Im Rahmen dieser Arbeit lag der Schwerpunkt auf der Identifizierung der Domänenwandcharakteristik und der
Untersuchung des thermischen Spinwellenspektrums. Zusätzliches Ziel war das Design von Antennenstrukturen zur Anregung von Spinwellen und deren Test. Erste Beobachtungen und Charakterisierungen des Spinwellenspektrums, sowohl thermisch aktivierter, als auch extern angeregter
Spinwellen, wurden mittels Brillouin-Lichtstreumikroskopie durchgeführt.
5.2.1 Untersuchung des thermischen Spinwellenspektrums
Bevor die eigentliche Untersuchung des Phasenverhaltens von kohärenten Spinwellen begonnen
werden konnte, wurde in ersten Messungen das Spektrum thermisch aktivierter Spinwellen be-
52
5.2 Charakterisierung des Spinwellenspektrums
obachtet und aufgenommen. Ein Grund dafür war zum einen die Bestimmung des echten Eigenmodenspektrum der untersuchten Struktur, welches nur durch die nicht invasive Untersuchung
thermischer Spinwellen garantiert werden kann, zum anderen war es wichtig herausfinden, welche Frequenzen des Spektrum sich für eine spätere resonante Anregung von Spinwellen überhaupt
eignen würden. Auch musste sichergestellt werden, dass überhaupt in den Messungen ein Unterschied zu sehen war zwischen einem Zustand, in dem eine Domänenwand initiiert war oder nicht.
Dieses hatte sich zwar in vorherigen Messungen mit dem Brillouin-Lichtstreumikroskop angedeutet [59], dennoch war es wichtig diesen Sachverhalt zu verifizieren. Die Messung des Spektrums
thermisch aktivierter Spinwellen fand entlang des Ni81 Fe19 -Halbkreises statt, die Messpunkte sind
in Abbildung 5.8 eingezeichnet. Dabei wurden an den jeweiligen Messpunkten für eine gewisse Zeit ein Spektrum aufgenommen und dann zum nächsten Messpunkt weitergefahren. Bei den
Messungen wurde der Ni81 Fe19 -Halbkreis mit Radius 10 µm gewählt. Wie man schon bei den
Untersuchungen der Domänenwände mit Hilfe der Lorentzmikroskopie erkennen konnte, spielt
der Radius des Halbkreises für die Art der Domänenwand keine Rolle, sondern erleichtert bzw.
erschwert lediglich das Entfernen einer Domänenwand. Im Laufe der Messungen wurden Magnet-
Abbildung 5.8: a) Skizze der Messanordnung. Entlang der roten Punkte wurden die Messungen durchgeführt. Eingezeichnet sind auch die externen Felder H parallel und Htransversal . Es wurde nur ein Spulenpaar
verwendet und für das Anlegen von H parallel wurde die Probe kurzzeitig um 90◦ gedreht und dann für die
eigentliche Messung wieder zurückgedreht. Dies garantierte einen identischen Messaufbau während der
ganzen Messreihe.
b) SEM-Aufnahme der Probe. Die roten Kreise deuten die Linie an, entlang derer gemessen wurde.
felder in paralleler und transversaler Richtung angelegt. Die Richtungen dieser Felder sind anhand
der Abbildung 5.8 gut zu erkennen. Die Realisation der magnetischen Felder im Experiment wurde
nur durch ein Spulenpaar realisiert, welches fest montiert war. Die Probe wurde nun so eingebaut,
dass man durch Anlegen eines Spulenstroms ein transversales Feld Htransversal erzeugen konnte.
Für das kurzzeitige Erzeugen eines parallelen Feldes H parallel wurde die Probe um 90◦ gedreht
und ein Strom an die Spule angelegt. Für die eigentliche Messung hingegen war die Anwesenheit von H parallel nicht notwendig, so dass die Probe wieder in die ursprüngliche Konfiguration
53
5.2 Charakterisierung des Spinwellenspektrums
zurückgedreht, bevor die Messung gestartet wurde. Somit hatte die Probe in allen Messungen ein
und dieselbe Position bzgl. des kompletten Brillouin-Lichtstreumikroskop-Aufbaus. Dieses hatte
zur Folge, dass die Polarisation des Lasers bzgl. der Magnetisierung bei allen Messungen gleich
war. Eine Änderung der Polarisation hätte mit Sicherheit zu unterschiedlichen Messergebnissen
geführt.
Abbildung 5.9 zeigt ein typisches Spektrum, wie es während der Messungen aufgenommen wurde. Man unterscheidet dabei zwischen dem Stokes-Bereich links vom Referenz-Signal und dem
Anti-Stokes-Bereich rechts vom Referenz-Signal. Neben dem Referenz-Signal erkennt man noch
das magnetische Signal der Ni81 Fe19 -Struktur und die höheren Ordnungen des Referenz-Signals
auf der linken und rechten Seite. Für die Messungen wurde nur der Stokes-Bereich aufgenommen,
da die für die Aufnahme des gesamten Spektrums benötigte Messzeit den zeitlichen Rahmen bei
weitem gesprengt hätte. Die Spektren der einzelnen Messpunkte wurden nun zu einer sogenannten
Abbildung 5.9: Typische Aufnahme eines Spektrums, aufgenommen mit dem Brillouin-Lichtstreumikroskop.
In der Mitte des Spektrums befindet sich das Referenzsignal. Links davon sieht man den Stokes-Bereich,
rechts den Anti-Stokes-Bereich. In beiden Bereichen erkennt man die magnetischen Signale ausgehend von
der untersuchten Ni81 Fe19 -Struktur und das Signal der höheren Ordnung des Referenz-Signals. Für die
Messung wurde nur der Stokes-Bereich aufgenommen.
Farbkarte (im weiteren Verlauf wird der englische Ausdruck colour map“ verwendet) zusammen”
gesetzt, wie sie Abbildung 5.10 zeigt. Bei ihr ist auf der x-Achse die Position und auf der y-Achse
die Frequenz aufgetragen. Die Intensität der Frequenz an der jeweiligen Position wurde farblich
kodiert, wobei die Farbskala von dunkelblau für geringe Intensität über grün und gelb für mittlere Intensitäten bis hin zu rot für hohe Intensitäten geht. Der Bereich des Referenz-Signals wurde
ausgeblendet, da dieses nicht das elastisch gestreute Licht von der Probe ist, sondern lediglich ein
54
5.2 Charakterisierung des Spinwellenspektrums
über das Shutter-System eingekoppelter kleiner Teil des Pumpstrahls. Außerdem wird durch die
Ausblendung die Übersichtlichkeit gesteigert. Bei den ersten Messungen wurden 71 Messpunkte
Abbildung 5.10: Farbkarte ( colour map“), zusammengesetzt aus den Spektren der einzelnen Messungen.
”
Die Abbildung links zeigt exemplarisch das Spektrum des 18. Messpunktes, der durch die orangene Linie
in der colour map“ gekennzeichnet ist. Bei der Farbkarte ist auf der x-Achse die Position und auf der y”
Achse die Frequenz aufgetragen. Die Intensität der Frequenz an der jeweiligen Position ist farbig dargestellt.
Die Farbskala reicht von dunkelblau für schwache Intensität über grün-gelb für mittlere Intensitäten bis
hin zu rot für hohe Intensitäten. Der Frequenzbereich bis 1,5 GHz ist ausgeblendet, da sich in ihm keine
Informationen bzgl. der untersuchten Struktur befinden (siehe Text).
entlang einer Linie erfasst, die in Abbildung 5.11 durch rote Kreise angedeutet ist. Die Strecke,
entlang derer gemessen wurde, ist 6,6 µm lang. Pro Messpunkt wurde nun für 65 Sekunden ein
Spektrum aufgenommen, so dass die Gesamtmessung in diesem Fall 76 Minuten dauerte. Die Probe wurde zuerst unter einem Winkel von 90◦ in das Mikroskop eingebaut, um ein paralleles Feld
H parallel anlegen zu können, so wie es weiter oben bereits beschrieben wurde. Durch das kurzzeitige Anlegen eines Feldes von etwa 1600 Oe wurde nun sichergestellt, dass die Probe vollständig
gesättigt wurde und etwaige Domänenwände entfernt wurden. Danach wurde die Probe wieder um
90◦ gedreht und in die bereits erwähnte Messposition gebracht. Die nun aufgenommene colour
”
map“ ist in Abbildung 5.11 dargestellt. Zur besseren Übersichtlichkeit ist wieder der Frequenzbereich des Referenz-Signals bis -1,5 GHz ausgeblendet. Durch zwei gestrichelte rote Linien ist
der Bereich der Ausstülpung gekennzeichnet. In der rechten oberen Ecke befindet sich der mit
OOMMF simulierte Zustand der Remanenz, in der sich auch die reale Probe befindet. In der co”
lour map“ kann man erkennen, dass sich stehende Spinwellen ausgebildet haben. Man kann gut
drei Moden erkennen, eine vierte ist schwächer angedeutet. Wie in Kapitel 2.2.1 bereits dargelegt,
handelt es sich um sogenannte Damon-Eshbach-Moden, deren Propagationsrichtung senkrecht zur
55
5.2 Charakterisierung des Spinwellenspektrums
Abbildung 5.11: colour map“ der Messung thermisch aktivierter Spinwellen in Abwesenheit einer
”
Domänenwand. Es haben sich stehende Spinwellen ausgebildet. Es handelt sich um magnetostatische Oberflächenmoden, die Aufgrund des begrenzten Volumens in transversaler Richtung quantisiert sind. Die leichte Verschiebung der Frequenzen der Spinwellen-Eigenmoden ist damit zu erklären, dass die Breite der
Ni81 Fe19 -Halbkreisstruktur herstellungsbedingt leicht variierte. Die Intensitätsabnahme der Moden ist auf
einen Drift des Fokus während der Messung zurückzuführen. Rechts oben ist ein Bild der zu diesem Zustand
gehörenden OOMMF-Simulation.
statischen Magnetisierung der Struktur ist. Durch die Reduzierung der Dimensionalität in transversaler Richtung kommt es bei magnetostatischen Oberflächenmoden zu einer Quantisierung, die
deutlich zu erkennen ist. Da bei dem Brillouin-Lichtstreumikroskop die Wellenvektoren nicht mehr
selektiv detektiert werden (siehe Kapitel 3.1.2), wird stattdessen das gesamte zur Verfügung stehende Spinwellenband aufgenommen. Somit steht fest, dass es sich bei den beobachteten Linien
in der colour map“ wirklich um diskretisierte Zustände handelt und diese Linien nicht durch eine
”
Wellenvektorselektivität, bedingt durch den Messaufbau, hervorgerufen wurden. Die Frequenzen
der ersten drei Moden liegen im Mittel bei 2,7 GHz, 4,2 GHz und 5,2 GHz. Dass man eine leichte
Verschiebung der Frequenzen hin zu höheren Werten sieht ist damit zu erklären, dass die Breite
der Ni81 Fe19 -Halbkreisstruktur nicht vollständig konstant war, sondern herstellungsbedingt leicht
variierte. Eine leichte Veränderung der Breite von nur 25 nm hat dann schon eine Verschiebung
um etwa 150 MHz zu Folge. Zum Vergleich wurden die Frequenzen der ersten drei magnetostatischen Oberflächenmoden mit Hilfe der Gleichung 2.41 aus Kapitel 2 berechnet. Die berechneten
Frequenzen liegen bei 3,7 GHz, 5,2 GHz und 6,2 GHz. Die effektive Breite des Streifens gemäß
Gleichung 2.45 wurde dabei berücksichtigt, ebenso wie die Tatsache, dass sich die Probe durch
den Laser aufheizt und damit die Sättigungsmagnetisierung MS auf etwa 650 · 103 A/m absinkt.
56
5.2 Charakterisierung des Spinwellenspektrums
Trotz dieser Modifikationen liegen die drei berechneten Frequenzen ein Gigahertz über den experimentell bestimmten Frequenzen. Jedoch ist der Abstand der Moden untereinander mit 1,5 GHz
zwischen der unteren und der mittleren Mode und 1 GHz zwischen der mittleren und der oberen
Mode beide Male gleich. Es handelt sich bei den drei beobachteten Moden also zweifelsfrei um
die ersten drei quantisierten magnetostatischen Oberflächenmoden. Die Abnahme der Intensität
mit fortschreitender Messposition ist damit zu erklären, dass die Probe während der Messung aus
dem Fokus driftete.
Als nächstes wurde für kurze Zeit ein externes transversales Magnetfeld Htransversal von etwa
1600 Oe angelegt und langsam wieder in den Zustand der Remanenz bei 0 Oe zurückgefahren.
Durch diese Vorgehensweise wurde eine Domänenwand in der Ni81 Fe19 -Struktur nukleiert. Da
die Ausstülpung als pinning center“ der Domänenwand, also als eine Art Haftzentrum“ für die
”
”
Domänenwand konzipiert wurde, war jetzt zu erwarten, dass sich die Domänenwand direkt unter der Ausstülpung oder zumindest in dessen Nähe befand. Die Untersuchungen der Strukturen
mit Hilfe der Lorentzmikroskopie und die mikromagnetischen Simulationen mit OOMMF deuteten deutlich auf ein solches Verhalten hin. Abbildung 5.12 zeigt nun tatsächlich eine erhebliche
Veränderung in der colour map“ der Messung nach der Nukleation der Domänenwand. Man er”
Abbildung 5.12: colour map“ der Messung thermisch aktivierter Spinwellen in Anwesenheit einer
”
Domänenwand. Es zeigt sich eine deutliche Veränderung gegenüber Messung ohne Domänenwand. Links
von der Position der Ausstülpung sind die ursprünglichen Moden verschwunden und eine neue Mode erscheint. Rechts oben befindet sich ein Bild der zu diesem Zustand gehörenden OOMMF-Simulation.
kennt, dass links von der Position der Ausstülpung die ursprünglichen Moden verschwinden und
57
5.2 Charakterisierung des Spinwellenspektrums
eine neue Mode unmittelbar vor der Ausstülpung erscheint. Eine Erklärung für dieses Verhalten liegt darin begründet, dass eine Domänenwand das effektive lokale Magnetfeld He f f verringert [12] und sich damit die Frequenz gemäß Glg. 2.41 ebenfalls verschiebt. Die Domänenwand
ändert ebenfalls den Winkel zwischen der Magnetisierung M und der Propagationsrichtung der
Spinwellen, so dass sich magnetostatische Backward“-Volumenmoden ausbilden.
”
Zusätzlich zu den bereits erwähnten Messungen wurden auch Messungen durchgeführt bei denen
ein externes transversales Feld Htransversal angelegt wurde. Anstatt der 71 Messpunkte wurden nun
100 Messpunkte aufgenommen, so dass sich der ausgemessene Bereich auf 9,6 µm erhöhte. Dadurch stieg die Messzeit auf 108 Minuten an. Als erstes wurde ein transversales Feld von 615 Oe
angelegt. Die colour map“ dazu ist in Abbildung 5.13 zu sehen. Man kann erkennen, dass bis
”
zu einer Position von 3,5 µm nur ein Frequenzband zwischen -6 und -7 GHz existiert. Ab 3,5 µm
kommt es zu einem Aufspalten des Frequenzbandes in zwei einzelne Resonanzen. Dabei bleibt
Abbildung 5.13: colour map“ der Messung, bei der ein transversales Feld Htransversal mit 615 Oe angelegt
”
war. Bis zu einer Position von 3,5 µm existiert nur ein Frequenzband zwischen -6 und -7 GHz. Danach wird
es in zwei einzelne Resonanzen aufgespaltet, wobei die obere Frequenz konstant über die gesamte Messung
bleibt. Die unter Frequenz hingegen nimmt ein Minimum kurz vor der Position der Ausstülpung an. Danach
steigt sie bis wieder ein gemeinsames Frequenzband entsteht.
die obere bezüglich ihrer Frequenz weitestgehend konstant in Hinsicht auf die Messposition. Die
untere Mode hingegen verringert ihre Frequenz stark bis sie kurz vor der Ausstülpung ein Minimum aufweist und anschließend wieder ansteigt, bis sich wieder ein gemeinsames Frequenzband
58
5.2 Charakterisierung des Spinwellenspektrums
bildet. Die zu diesem Zustand gehörende OOMMF-Simulation in Abbildung 5.13 zeigt, dass bereits bei diesem Feld keine Domänenwand mehr im Bildbereich vorhanden ist. Die Bezeichnung
der Frequenzverringerung scheint im ersten Augenblick etwas verwunderlich, da in der colour
”
map“ die Frequenzen negativ angegeben sind. Allerdings muss beachtet werden, dass die Beträge
der Frequenzen zu betrachten sind, da im Stokes-Bereich gemessen wurde (siehe Abb. 5.9) und
man äquivalent den Anti-Stokes-Bereich hätte verwenden können. Somit sind die Angaben der
Frequenzen immer bezüglich des Referenz-Signals einzuordnen. Abbildung 5.14 zeigt, dass das
Frequenzband bei einem transversalem Feld von 814 Oe nun etwas höher beginnt, und zwar bei
-7 bis -8 GHz. Auch setzt das Aufspalten des Frequenzbandes in zwei einzelne Spinwellen-Moden
bereits bei 2,5 µm ein. Die Frequenz der unteren Resonanz verringert sich nicht mehr so stark. Da
sich die obere Mode wieder konstant bezüglich ihrer Frequenz verhält, ist also die Aufspaltung
insgesamt nicht mehr so ausgeprägt, allerdings ist sie jetzt bis zur Position bei 9,6 µm sichtbar.
Bei einem angelegten transversalen Feld von 1296 Oe beginnt das Frequenzband nun zwischen
Abbildung 5.14: colour map“ der Messung mit einem angelegten Feld Htransversal von 814 Oe. Das Fre”
quenzband startet nun bereits bei -7 bis -8 GHz. Das Aufspalten dieses Frequenzbandes beginnt nun schon
bei einer Position von 2,5 µm, allerdings ist diese Aufspaltung nicht mehr so ausgeprägt, da die untere
Frequenz sich nicht mehr so stark verringert und die obere Frequenz weiterhin konstant bleibt.
-9 bis -10 GHz, wie in Abbildung 5.15 zu erkennen ist. Auch das Aufspalten in zwei einzelne
Spinwellen-Eigenmoden zeigt sich nun bereits nach einem Mikrometer. Die Frequenz der unteren Mode verringert sich dabei nur noch schwach und hat ihr Minimum bei 6,5 GHz. Dennoch
59
5.2 Charakterisierung des Spinwellenspektrums
bleibt die Aufspaltung bis zur Position bei 9,6 µm erhalten. Die obere Resonanz hingegen bleibt
wie bei den Messungen zuvor konstant entlang der gemessenen Positionen. Zusammenfassend
Abbildung 5.15: ”colour map”der Messung diesmal mit einem angelegten Feld Htransversal von 1296 Oe. Das
Frequenzband beginnt zwischen -9 bis -10 GHz. Das Aufspalten in zwei einzelne Spinwellen-Eigenmoden
ist bereits nach einem µm zu erkennen. Die Aufspaltung ist jedoch nicht mehr so ausgeprägt, da die untere
Mode sich nur noch bis 6,5 GHz absenkt und die obere Mode wie schon zuvor konstant bezüglich ihrer
Frequenz bleibt.
lässt sich bei den Messungen mit angelegtem Feld erkennen, dass eine Eigenmode nach der Aufspaltung des ursprünglichen Frequenzbandes eine konstante Frequenz aufweist, diese Frequenz
wie erwartet mit steigendem Feld ansteigt. Das ist damit erklärbar, dass bei der Messung Back”
ward“-Volumen-Geometrie vorlag und gemäß Gleichung 2.42 die Frequenzen der Eigenmoden mit
steigendem angelegten Feld Htransversal ebenfalls ansteigen. Die zweite Eigenmode hingegen verringert ihre Frequenz bis zu einer Position direkt vor der Ausstülpung. Allerdings wandert dieses
Minimum mit steigendem Feld ebenfalls hoch, so dass sich insgesamt betrachtet der Abstand zwischen den beiden Moden bei höheren Feldern verringert und somit auch die Aufspaltung immer
kleiner wird.
60
5.2 Charakterisierung des Spinwellenspektrums
5.2.2 Untersuchung angeregter Spinwellen
Die Untersuchung der Wechselwirkung von kohärenten Spinwellen mit Domänenwänden ist wie
bereits zuvor erwähnt, das Ziel aktueller Forschungen. Kohärente Spinwellen können in diesem
Zusammenhang durch externe Anregung des Spinsystems erzeugt werden. Dieses Unterkapitel
beschäftigt sich mit der Anregung von Spinwellen durch Mikrostreifenleiter. Wie bereits im Kapitel 4.2 über die Probenpräparation erläutert war es nicht möglich, mit den Proben, mit denen
das Spektrum thermischer Spinwellen untersucht wurde, Spinwellen mit Hilfe der Mikrowellenantenne anzuregen. Die Neuerungen, die die verbesserten Proben der zweiten Serie aufweisen,
sind detailliert in Kapitel 4.2 beschrieben. Es war daher von großem Interesse zu überprüfen, ob
überhaupt mit dieser Art von Proben eine Anregung von Spinwellen möglich ist.
Analog zu den vorherigen Messungen im Brillouin-Lichtstreumikroskop wurde wieder entlang der
Ni81 Fe19 -Strukturen gemessen. Abbildung 5.16 zeigt die Messpunkte, angedeutet als rote Kreise, sowohl für die untersuchten Halbkreise als auch für die Streifenstrukturen, an denen ebenfalls Untersuchungen durchgeführt wurden. Die Nullposition befand sich immer an dem Punkt,
an dem sich die Antenne und die zu untersuchende Ni81 Fe19 -Struktur direkt treffen. Im Lau-
Abbildung 5.16: a) Skizze der Messanordnung für einen Ni81 Fe19 -Halbkreis. Entlang der roten Kreise wurden die Messungen durchgeführt. Die externen Felder Htransversal und H parallel wurden analog zur vorherigen Messreihe definiert.
b) Skizze der Messanordnung für einen einfachen Ni81 Fe19 -Streifen. Zusätzlich wurden noch einmal
Htransversal und H parallel eingezeichnet.
Die Startposition bei allen Messungen befand sich bei allen Messungen an der Position, an der die Struktur
auf die Antenne trifft. Die Messrichtung führt demzufolge von der Antenne weg.
fe der Messungen wurden wieder Magnetfelder in paralleler und transversaler Richtung ange61
5.2 Charakterisierung des Spinwellenspektrums
legt, um Domänenwände zu nukleieren bzw. wieder zu entfernen, wie schon in Abschnitt 5.2.1
ausführlich beschrieben wurde. Das Magnetfeld in transversaler Richtung Htransversal wurde wie
zuvor durch ein Spulenpaar erzeugt. Da nun aber die Probe aufgrund der Kontaktierung mit der
Mikrowellenquelle fest eingebaut war, musste für die Erzeugung des parallelen Feldes H parallel
ein kleiner Permanentmagnet aus Nd2 Fe14 B2 verwendet werden. Der Permanentmagnet erzeugt
dabei im Abstand von 0,5 cm ein Feld von 2200 Oe und ist somit ausreichend stark, um die
Domänenwandnukleation durchführen zu können. Als Quelle für die Mikrowellen wurde ein Mikrowellengenerator ( HP 8672A) verwendet, der über einen Frequenzbereich von 2-18 GHz eine
Ausgangsleistung von bis zu 10 dBm liefert. Zusätzlich wurde noch ein Mikrowellenverstärker benutzt, der über den gesamten Frequenzbereich eine mittlere Verstärkung von 30 dBm liefert, so dass
insgesamt eine mittlere Verstärkung von 40 dBm zur Verfügung steht. Mit Hilfe eines Netzwerkanalysators wurde allerdings festgestellt, dass aufgrund von Verlusten und durch Rückreflexionen
nur etwa 29 dBm Leistung an der Probe ankommen.
Die Anregung des Spinsystems wird durch das Oersted-Feld der Antenne verursacht. Mit dem
Oersted-Feld wird das Magnetfeld eines stromdurchflossenen Leiters bezeichnet. Mit Hilfe des
Biot-Savart-Gesetzes können nun die verschiedenen Komponenten dieses Magnetfeldes in Abhängigkeit zum Abstand zur Antenne berechnet werden. Abbildung 5.17 zeigt die Feldverteilung der
relevanten Komponente in der Ebene und senkrecht zur Ebene in Abhängigkeit zum Abstand der
Antenne. Die z-Komponente des Magnetfeldes (siehe Abb. 5.17) liegt senkrecht zu den Ni81 Fe19 Strukturen und somit auch senkrecht zur Magnetisierung der Probe. Gemäß der Landau-Lifschitzund Gilbert-Gleichung 2.13 ist damit der Drehmomentübertrag maximal. Die x-Komponente des
Oersted-Feldes kann hingegen kein Drehmoment auf die Magnetisierung ausüben. Aus diesem
Grund wird im weiteren Verlauf nur die z-Komponente des Magnetfeldes in die Betrachtungen mit
einbezogen.
Vor Beginn der Messungen wurde für die jeweilige Struktur zuerst die Frequenz der ferromagnetischen Resonanz (FMR) bestimmt, indem die Brillouin-Lichtstreuintensität an einem Punkt
vermessen und die Frequenz mit der höchsten Intensität als FMR-Frequenz identifiziert wurde.
Die FMR-Frequenz lag in dem hier vorliegenden Fall bei 2,2 GHz. Abbildung 5.18 zeigt eine
colour map“ der Messung der angeregten ferromagnetischen Resonanz in einem 500 nm breiten
”
Ni81 Fe19 -Streifen, ohne dass eine Domänenwand initiiert wurde. Die Ausstülpung ragt 250 nm
aus dem Streifen heraus. Die Startposition (x = 0 µm) der Messung befand sich an der Stelle,
an der der Streifen auf die Antenne trifft (siehe Abb. 5.17), die Endposition am Ende des Streifens nach 12 µm. Anschließend wurde die Nukleation der Domänenwand nach dem Prinzip durchgeführt, wie es schon im vorherigen Unterkapitel erläutert wurde. Abbildung 5.19 zeigt die Intensitätsprofile des gemessenen Brillouin-Lichtstreu-Signals bei Anregung mit der ferromagneti2 Neodym-Eisen-Bor
62
5.2 Charakterisierung des Spinwellenspektrums
Abbildung 5.17: x- und z-Komponente des Magnetfeldes der Antenne in Abhängigkeit von der x-Position.
Die Definition der Raumrichtungen ist dabei der Schemaskizze rechts oben zu entnehmen. Das Magnetfeld
entsteht gemäß des Biot-Savart-Gesetzes durch die Stromdichte j durch die Antenne in y-Richtung. Die zKomponente des Magnetfeldes ist deutlich stärker und hat eine größere Reichweite als die x-Komponente.
Daher wird im Folgenden auch ausschließlich die z-Komponente zur Berechnung verwendet.
schen Resonanzfrequenz je einmal vor und nach der Nukleation einer Domänenwand. Es ist deutlich ein starker exponentieller Abfall in beiden Fällen erkennbar, wie es bei einer Anregung mit
der FMR-Frequenz zu erwarten ist, da keine Spinwellen mit von Null verschiedenem Wellenvektor angeregt werden. Dieses bestätigt sich bei Betrachtung der logarithmischen Darstellung oben
rechts in Abbildung 5.19. Beide Intensitätsprofile zeigen einen starken, rein exponentiellen Abfall und schon ab der Mitte der Struktur können keine Spinwellen mehr nachgewiesen werden.
Mit Hilfe der eingezeichneten Regressionsgeraden wurde die Abklinglänge der ferromagnetischen
Resonanz bestimmt. So beträgt die Abklinglänge vor der Nukleation einer Domänenwand 4,2 µm
und danach 4,5 µm. An welcher Stelle sich nun die Domänenwand befindet bzw. ob überhaupt eine
Domänenwand bei dieser Messung präsent war kann jedoch nicht exakt bestimmt werden, da die
Nukleation einer Domänenwand in einem geraden Streifen trotz Ausstülpung im Vergleich zu den
gebogenen Strukturen mit einer wesentlich geringeren Wahrscheinlichkeit stattfindet. Eine weitere
Möglichkeit wäre, dass sich die Domänenwand von dem Startpunkt aus gesehen hinter der Ausstülpung befände. An dieser Stelle wäre jedoch der Einfluss der Domänenwand auf die bereits stark
abgeklungene ferromagnetische Resonanz gering. Zusätzlich zur Intensität wurde in Abbildung
63
5.2 Charakterisierung des Spinwellenspektrums
Abbildung 5.18: Messung der Spinwellenintensität bei Anregung mit der ferromagnetischen Resonanzfrequenz bei 2,2 GHz vor der Nukleation einer Domänenwand. Die Messung wurde in einem 500 nm breiten
Ni81 Fe19 -Streifen durchgeführt. Eingezeichnet ist die Position der Ausstülpung, die 250 nm aus dem Streifen herausragt.
5.19 noch die z-Komponente des von der Antenne erzeugten Oersted-Feldes eingezeichnet. Die
z-Komponente ist, wie bereits erwähnt, dafür verantwortlich, dass die Magnetisierung überhaupt
angeregt wird. Vergleicht man den Verlauf des durch die Mikrowellenantenne erzeugten Magnetfeldes mit den gemessenen Spinwellen-Intensitäten so wird deutlich, dass das Magnetfeld sehr viel
stärker abfällt, als die Intensität der Spinwellen. Damit kann mit recht hoher Wahrscheinlichkeit
ausgeschlossen werden, dass die in einigem Abstand von der Antenne gemessenen Spinwellen
nicht direkt durch das von der Antenne generierte Oerstedfeld erzeugt werden.
Da das eigentliche Interesse der Anregung propagierender Spinwellen mit einem von null verschiedenen Wellenvektor gilt, wurde nun mit 2,4 GHz eine Frequenz gewählt, die sich von der
ferromagnetischen Resonanzfrequenz unterschied. Abbildung 5.20 zeigt die Intensität der mit
2,4 GHz angeregten Mode in dem selben Ni81 Fe19 -Streifen, der schon zuvor gewählt wurde. Dieses
Mal ist ein deutlicher Unterschied zwischen der Anregung vor und nach der Initialisierung einer
Domänenwand erkennbar. Dieses deutet darauf hin, dass sich die Domänenwand in einem Bereich
befindet, in dem die angeregte Mode noch nicht zu stark abgeklungen ist. Durch die Domänenwand
wird das effektive interne Feld durch das Entmagnetisierungsfeld stark verringert und die angeregte Mode befindet sich nicht mehr in Resonanz, was den gemessenen Intensitätseinbruch an dieser
Stelle erklärt. In der logarithmischen Darstellung in Abbildung 5.20 oben rechts sind zwei unter-
64
5.2 Charakterisierung des Spinwellenspektrums
Abbildung 5.19: Intensitätsprofile der gemessenen Spinwellen bei Anregung mit der Ferromagnetischen Resonanzfrequenz bei 2,2 GHz vor und nach der Nukleation einer Domänenwand in einem Ni81 Fe19 -Streifen
mit einer Breite von 500 nm. Charakteristisch ist der starke exponentielle Abfall der FMR. Diese Beobachtung wird durch die logarithmische Darstellung oben rechts gestützt, bei der beide Intensitätsprofile einen
linearen Abfall zeigen. Die Abklinglängen wurden durch die eingezeichneten Regressionsgeraden bestimmt.
schiedliche Bereiche erkennbar. Der erste Bereich hat die gleiche Abklinglänge von 4,3 µm, wie
in der zuvor beschriebenen Messung, bei der nur mit der FMR-Frequenz angeregt wurde. In dem
von der Antenne weiter entfernten Bereich des Streifens können Spinwellen nachgewiesen werden,
deren Abklinglänge nun 11,1 µm beträgt, und nun sogar bis zum Ende der Struktur beobachtet werden. Der grau schattierte Bereich in der logarithmischen Darstellung ist somit der experimentelle
Nachweis, dass mit der verwendeten Anregungstechnik effektiv propagierende Spinwellen in einem mikrostrukturierten Permalloy-Streifen erzeugt werden können. Zusätzlich zu den Messungen
in Ni81 Fe19 -Streifen wurden angeregte Spinwellen in den bereits erwähnten Ni81 Fe19 -Halbkreisen
durchgeführt. In Abbildung 5.21 ist die Intensität der mit 2,4 GHz angeregten Resonanz in dem
Halbkreis mit einer Breite von 400 nm und einem Radius von 10 µm zu sehen. Die Ausstülpung
ragte wieder um 250 nm aus dem Halbkreis heraus. Ein Unterschied in der Intensität der Mode
vor und nach der Nukleation der Domänenwand ist auch diesmal deutlich erkennbar, jedoch nicht
so ausgeprägt wie im vorangegangenen Fall. Bei der Betrachtung der logarithmischen Darstellung
zeigen sich drei unterschiedliche Bereiche, wobei der erste wieder von der Anregung der FMR
dominiert wird. Der zweite, grau unterlegte Bereich zeigt wieder angeregte Spinwellen.
Abschließend lässt sich sagen, dass mit den entworfenen Antennenstrukturen Spinwellen ange-
65
5.2 Charakterisierung des Spinwellenspektrums
Abbildung 5.20: Intensitätsprofile einer angeregten Mode bei 2,4 GHz in der selben Messkonfiguration wie
in Abb. 5.20. Deutlich erkennbar ist der Unterschied vor und nachdem eine Domänenwand initialisiert
wurde. In der logarithmischen Darstellung oben rechts sind zwei verschiedene Bereiche zu erkennen, von
denen der erste weiterhin durch den starken Abfall der FMR bestimmt wird. Der zweite Bereich zeigt eine
deutlich größere Abklinglänge und ist ein deutlicher Hinweis auf propagierende Spinwellen.
regt werden konnten und die Abklinglänge bestimmt wurde. Des weiteren wurde ein deutlicher
Unterschied bei An- und Abwesenheit einer Domänenwand beobachtet.
66
5.2 Charakterisierung des Spinwellenspektrums
Abbildung 5.21: Bei dem Ni81 Fe19 -Halbkreis mit einem Radius von 10 µm ist wieder ein Unterschied in der
Intensität der mit 2,4 GHz angeregten Mode vor und nach der Nukleation der Domänenwand erkennbar,
jedoch nicht so ausgeprägt wie zuvor. In der logarithmischen Darstellung oben rechts sind drei unterschiedliche Bereiche zu sehen. Der erste Bereich wird von der FMR dominiert, der zweit, grau unterlegte zeigt
angeregte Spinwellen, die in diesem Fall frei propagieren und im dritten Bereich sind die angeregten Spinwellen nicht mehr von der Dunkelzählrate zu unterscheiden.
67
KAPITEL 6
Zusammenfassung und Ausblick
Ziel der vorliegenden Diplomarbeit war die Untersuchung der Wechselwirkung von Spinwellen
mit Domänenwänden in Ni81 Fe19 -Nanostreifen. Wichtig hierfür war einerseits die Anregung von
Spinwellen und Untersuchung des Spinwelleneigenspektrums der Nanostreifen und andererseits
die Charakterisierung der Domänenwandnukleation an speziell dafür integrierten Haftzentren. Die
Untersuchung des Spinwelleneigenspektrum wurde mit Hilfe der in der Arbeitsgruppe Hillebrands
etablierten Brillouin-Lichtstreumikroskopie durchgeführt. Die Untersuchung der Domänenstruktur
erfolgte mittels Lorentzmikroskopie im Rahmen einer Kooperation mit der Arbeitsgruppe von
Prof. John N. Chapman an der Universität Glasgow.
Um die gewünschten Untersuchungen an Ni81 Fe19 -Nanostreifen realisieren zu können, war es notwendig, ein Probendesign zu finden, dass es ermöglichte, Domänenwände definiert zu pinnen und
die Wechselwirkung dieser gepinnten Wände mit Spinwellen untersuchen zu können. Da die Charakterisierung des Spinwelleneigenspektrums keine in-situ-Charakterisierung der Domänenkonfiguration in den Nanostreifen erlaubt, war es hierbei essentiell, dass durch einfache experimentelle
Schritte die Domänenwandnukleation reproduzierbar realisiert werden kann. Diese Anforderungen
erfüllt eine in der Literatur als sogenanntes Domänenwandpendel“ bekannte Halbkreisstruktur, in
”
deren Pol zum Zweck des Pinnens der nukleierten Domänenwand hier eine Ausstülpung als Haftzentrum eingeführt wurde. Die untersuchten Ni81 Fe19 -Nanostreifen hatten eine Schichtdicke von
10 nm und eine Streifenbreite von 500 nm. Der Radius des Halbkreises wurde in 5 µm Schritten
von 5 µm bis 50 µm variiert. Die halbkreisförmige Ausstülpung hatte einen Radius von 250 nm.
Die Anregung von Spinwellen in den Ni81 Fe19 -Nanostreifen wurde über eine impedanzangepasste
mikrostrukturierte Mikrowellenantenne aus 150 nm Gold realisiert. Die Proben wurden mit einer
Kombination aus Elektronenstrahllithographie und Molekularstrahlepitaxie bzw. Elektronenstrahlverdampfung hergestellt.
Die Magnetisierungsverteilung in den zu untersuchenden Ni81 Fe19 -Halbkreisstrukturen wurde unter besonderer Berücksichtigung der sich herausbildenden Domänenwände zunächst mit Hilfe
mikromagnetischer Simulationen (OOMMF-Code [57]) berechnet und die Struktur hinsichtlich
verschiedener Parameter wie z.B. der Schichtdicke oder Streifenbreite optimiert. Zur experimen-
68
tellen Verifikation dieser Simulationsergebnisse wurden die Ni81 Fe19 -Nanostreifen im Lorentzmikroskop charakterisiert. Hierfür ist eine Probenpräparation auf speziellen elektronentransparenten Si3 N4 /Si-Fenstersubstraten mit einer Membrandicke von 50 nm erforderlich, die im Rahmen dieser Arbeit am Nano+Bio Center der TU Kaiserslautern eingeführt wurde. Die Ergebnisse
der OOMMF-Simulationen und der Lorentzmikroskopie ergaben übereinstimmend, dass in der
gewählten Probenstruktur die Nukleation einer sogenannten asymmetrischen Domänenwand beobachtet wird, die an der Ausstülpung wie gewünscht haftet.
Ziel der Untersuchung der Spinwellen in diesen Ni81 Fe19 -Nanostreifen war zum einen die Bestimmung des Spektrums thermisch aktivierter Spinwellen und zum anderen mikrowellenangeregter Spinwellen in Anwesenheit und Abwesenheit einer Domänenwand. Beim Eigenspektrum der
thermisch aktivierten Spinwellen konnte ein signifikanter Unterschied zwischen den Spektren in
Anwesenheit einer Domänenwand und ohne Domänenwand festgestellt werden. Dies ist auf die
Änderung des internen Feldes im Bereich der Domänenwand zurückzuführen, die bewirkt, dass an
der Position der Wand die ursprünglichen Spinwellenmoden verschwinden und neue entstehen, die
nur in diesem Bereich existieren. Auf diese Weise wurde erfolgreich demonstriert, dass sich mit
Hilfe der Brillouin-Lichtstreuspektroskopie die Existenz einer Domänenwand nachweisen lässt.
Zur Anregung von Spinwellen mittels Mikrowellen stellte sich im Rahmen der Untersuchungen
heraus, dass das ursprünglich gewählte Design der einseitig kurzgeschlossenen Antenne verworfen werden musste, da es keine Fehlersuche z.B. unter Anwendung eines Netzwerkanalysators
erlaubt. Mit der verbesserten Antennenstruktur konnten schließlich erfolgreich Spinwellen in den
Ni81 Fe19 -Nanostreifen angeregt und ihre Abklinglänge bestimmt werden. Wie im Falle der thermischen Spinwellen konnten hier ebenfalls deutliche Unterschiede im Eigenspektrum bei An- bzw.
Abwesenheit einer Domänenwand festgestellt werden.
Die hier vorliegende Arbeit zeigt, dass es bei geeignetem Probendesign möglich ist, den Einfluss definierter Domänenwände auf das Spinwelleneigenspektrum in Ni81 Fe19 -Nanostreifen mittel Brillouin-Lichtstreumikroskopie zu studieren. Aufbauend auf den hier erzielten Resultaten ist
als nächster Schritt eine systematische Untersuchung der Wechselwirkung der angeregten Spinwellen mit Domänenwänden notwendig, um die physikalischen Hintergründe im Detail analysieren zu
können. Ein wesentlicher Aspekt hierbei ist, wie sich die Phase der Spinwellen beim Passieren der
Wand verändert. Um diese Untersuchungen durchführen zu können, wird der momentane Aufbau
des Brillouin-Lichstreumikroskops derzeit erweitert, um sowohl zeit- als auch phasenaufgelöste
Messungen zu ermöglichen. Weiterhin sind die Bestimmung von Transmissions- und Reflexionskoeffizienten von Spinwellen in Ni81 Fe19 -Nanostreifen von Interesse.
69
Literaturverzeichnis
[1] J. M. Slaughter, R. W. Dave, M. DeHerrera, M. Durlam, B. N. Engel, J. Janesky, M. D. Rizzo,
und S. Tehrani, Fundamentals of MRAM Technology, J. Supercond. 15, 19 (2002).
[2] S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnar, M. L. Roukes,
A. Y. Chtchelkanova, und D. M. Treger, Spintronics: A Spin-Based Electronics Vision for the
Future, Science 294, 1488 (2001).
[3] D. A. Allwood, G. Xiong, M. D. Cooke, C. C. Faulkner, D. Atkinson, N. Vernier, und R. P.
Cowburn, Submicrometer Ferromagnetic NOT Gate and Shift Register, Science 296, 2003
(2002).
[4] D. A. Allwood, G. Xiong, C. C. Faulkner, D. Atkinson, D. Petit, und R. P. Cowburn, Magnetic
Domain-Wall Logic, Science 309, 1688 (2005).
[5] A. Hubert und R. Schäfer (Herausgeber) Magnetic domains, Springer, Berlin, Heidelberg,
New York (1999).
[6] F. Bloch, Zur Theorie des Austauschproblems und der Remanenzerscheinung der Ferromagnetika, Z. Phys A 74, 295 (1932).
[7] L. Neél, Energie des parois de Bloch dans les couches minces, C.R. Acad. Science 241, 533
(1955).
[8] W. Döring, Über die Trägheit der Wände zwischen Weißschen Bezirken, Z. Naturf. 3a(7), 373
(1948).
[9] C. Chappert und T. Devolder, A magnetic pendulum, Nature 432, 162 (2004).
[10] E. Saitoh, H. Miyajima, T. Yamaoka, und G. Tatara, Currrent-induced resonance and mass
determination of a single magnetic domain wall, Nature 432, 203 (2004).
[11] H. Dötsch, H. Schmitt, und J. Müller, Detection and generation of magnetic bubble domains
using ferrimagnetic resonance, Appl. Phys. Lett. 23, 639 (1973).
70
LITERATURVERZEICHNIS
[12] C. Bayer, H. Schultheiß, B. Hillebrands, und R. L. Stamps, Phase Shift of Spin Waves Traveling Through a 180◦ Bloch-Domain Wall, IEEE Trans. Mag. 41, 3094 (2005).
[13] S. Chikazumi, Physics of Ferromagnetism, 2. Auflage, Oxford University Press, Oxford, New
York (1997).
[14] E. C. Stoner und E. P. Wohlfahrt, A mechanism of magnetic hysteresis in heterogeneous alloys, Philos. Trans. London Ser. A 240, 599 (1948).
[15] C. Cohen-Tannoudji, B. Diu, und F. Laloë, Quantenmechanik, Band 2, 2. Auflage, Walter de
Gruyter, Berlin, New York (1999).
[16] L. Landau und E. Lifshitz, On the theory of the dispersion of magnetic permeability in ferromagnetic bodies, Phys. Z. Sowjetunion 8, 153 (1935).
[17] J. C. Mallison, On Damped Gyromagnetic Precession, IEEE Trans. on Magn. 23(4), 2003
(1987).
[18] T. L. Gilbert, A phenomenological Theory of Damping in Ferromagnetic Materials, IEEE
Trans. on Magn. 40(6), 3443 (2004).
[19] H. Suhl, Theory of the magnetic damping constant, IEEE Trans. Magn. 34(4), 1834 (1998).
[20] J. D. Jackson, Klassische Elektrodynamik, 3. Auflage, Walter de Gruyter, Berlin, New York
(2002).
[21] W. Nolting, Quantentheorie des Magnetismus, Teubner (1997).
[22] D. D. Stancil, Theory of Magnetostatic Waves, Springer, New York, Berlin, Heidelberg
(1993).
[23] B. A. Kalinkos und A. N. Slavin, Theory of dipole-exchange spin wave spectrum for ferromagnetic films with mixed exchange boundary conditions, J. Phys. C: Solid State Phys. 19,
7013 (1986).
[24] C. Kittel, On the theory of ferromagnetic resonance absorption, Phys. Rev. 73(2), 155 (1948).
[25] C. Herring und C. Kittel, On the theory of spinwaves in ferromagnetic media, Phys. Rev. 81,
869 (1951).
[26] R. W. Damon und J. R. Eshbach, Magnetostatic Modes of a Ferromagnetic Slab, J. Appl.
Phys. 31, 104 (1960).
71
LITERATURVERZEICHNIS
[27] H. Schultheiß, Brillouin-Lichtsteu-Mikroskopie an magnetischen Mikrostrukturen, Diplomarbeit, TU Kaiserslautern (2005).
[28] S. O. Demokritov, Brillouin Light Scattering Studies of Confined Spin Waves: Linear and
Nonlinear Confinement, Physics Reports 348, 441–489 (2001).
[29] J. Jorzick, C. Krämer, S. O. Demokritov, B. Hillebrands, B. Bartenlian, C. Chappert, D. Decanini, F. Rousseaux, E. Cambril, E. Søndergard, M. Bailleul, C. Fermon, und A. N. Slavin,
Spin wave quantization in laterally confined magnetic structures, J. Appl. Phys. 89, 7091
(2001).
[30] J. Jorzick, S. O. Demokritov, B. Hillebrands, D. Berkov, N. L. Gorn, K. Guslienko, und A. N.
Slavin, Spin wave wells in nonellipsoidal micrometer size magnetic elements, Phys. Rev. Lett.
88, 047204 (2002).
[31] B. Hillebrands und J. Hamrle, Investigation of Spin Waves and Spin Dynamics by Optical
Techniques, in: H. Kronmüller und S. Parkin (Herausgeber) Handbook of Magnetism and
Advanced Magnetic Materials, Kapitel 20, John Wiley and Sons, Ltd. (2007).
[32] K. Y. Guslienko, S. O. Demokritov, B. Hillebrands, und A. N. Slavin, Effective dipolar boundary conditions for dynamic magnetization in thin magnetic stripes, Physical Review B 66,
132402 (2002).
[33] Y. Nakatani, A. Thiaville, und J. Miltat, Head-to-head domain walls in soft nano-strips: a
refined phase diagram, J. Magn. Magn. Mater. 291, 750 (2005).
[34] R. D. McMichael und M. J. Donahue, Head to head domain walls structures in thin magnetic
strips, IEEE Trans. Magn. 33, 4167 (1997).
[35] A. Yamaguchi, T. Ono, S. Nasu, K. Miyake, K. Mibu, und T. Shinjo, Real-Space Observation
of Current-Driven Domain Wall Motion in Submicron Magnetic Wires, Phys. Rev. Lett. 92,
077205 (2004).
[36] M. Laufenberg, D. Backes, W. Bührer, D. Bedau, M. Kläui, U. Rüdiger, C. A. F. Vaz, J. A. C.
Bland, L. J. Heyderman, F. Nolting, S. Cherifi, A. Locatelli, R. Belkhou, S. Heun, und E. Bauer, Observation of thermally activated domain wall transformations, Appl. Phys. Lett. 88,
052507 (2006).
[37] J. R. Sandercock, Trends in Brillouin Scattering: Studies of Opaque Materials, Supported
Films, and Central Modes, in: M. Cardona und G. Güntherodt (Herausgeber) Light scattering
in solids III. Recent Results, Topics in applied physics, Band 51, Springer, Berlin, Heidelberg,
New York (1982).
72
LITERATURVERZEICHNIS
[38] B. Hillebrands, Brillouin light scattering from layered magnetic structures, in: M. Cardona
und G. Güntherodt (Herausgeber) Light Scattering in Solids VII in : Topics in Applied Physics
75, Springer (1999).
[39] B. Hillebrands, Brillouin light scattering spectroscopy, in: Y. Zhu (Herausgeber) Novel techniques for characterizing magnetic materials, Springer (2005).
[40] J. R. Sandercock, Tandem-Fabry-Perot Interferometer TFP-1 (May 2001).
[41] W. L. Johnson und P. Kabos, Brillouin light scattering from pumped uniform precession and
low-k magnons in Ni81 Fe19 , Appl. Phys. Lett. 86, 102507 (2005).
[42] J. Jorzick, S. O. Demokritov, C. Mathieu, B. Hillebrands, B. B. C. Chappert, F. Rousseaux,
und A. Slavin, Brillouin Light Scattering from quantized spinwaves in micron-size magnetic
wires, Phys. Rev. B 60, 15194 (1999).
[43] E. Hecht, Optik, 4. Auflage, Oldenbourg, München, Wien (2005).
[44] C. Bayer, J. P. Park, H. Wang, M. Yan, C. E. Campbell, und P. A. Crowell, Spin Waves in an
Inhomogeneously Magnetized Stripe, Phys. Rev. B 69, 134401 (2004).
[45] J. N. Chapman, The investigation of magnetic domain structures in thin film foils by electron
microscopy, J. Phys. D: Appl. Phys. 17, 623 (1984).
[46] J. N. Chapman und M. R. Scheinfein, Transmission electron microscopies of magnetic microstructures, Jour. Magn. Magn. Mat. 200, 729 (1999).
[47] A. Hubert und R. Schäfer, Magnetic domains, Springer, Berlin, Heidelberg, New York (2000).
[48] N. Wiese, Lorentz TEM Imaging, Multimat Meeting, Oxford UK (2007).
[49] B. Khamsehpour, C. D. W. Wilkinson, und J. N. Chapman, Use of laser reflectometry for
end-point detection during the etching of magnetic thin films, J. Vac. Sci. Technol. A 15,
2069 (1997).
[50] Y. Aharonov und D. Bohm, Significance of Electromagnetic Potential in the Quantum Theory,
Phys. Rev. 115, 485 (1959).
[51] R. P. Cowburn, mündliche Mitteilung (2006).
[52] R. Waser (Herausgeber) Nanoelectronics and Information Technology, Wiley-VCH, Weinheim (2003).
73
LITERATURVERZEICHNIS
[53] P. Rai-Choudhury (Herausgeber) Handbook of Microlithography, Micromachining and Microfabrication, SPIE, Optical Engineering Press, Washington, USA (1997).
[54] M. Bailleul, Propagation et confinement d’onde de spin dans les microstructures
magnétiques, Dissertation, CEA Saclay (2002).
[55] R. N. Simons, Coplanar Waveguide Circuits, Components, and Systems, Wiley and Sons
(2001).
[56] H. Hasegawa, M. Furukawa, und H. Yanai, Properties of microstrip line on Si-SiO2 system,
IEEE Trans. on MTT 19, 869 (1971).
[57] M. J. Donahue und D. G. Porter, Oommf user’s guide, version 1.0, Interagency, Report
NISTIR 6276, National Institute of Standards and Technology, Gaithersburg, MD (1999).
[58] S. Schäfer, Magnetisierungsdynamik in mesoskopischen Ni81 Fe19 -Ringstrukturen, Diplomarbeit, TU Kaiserslautern (2007).
[59] K. Perzlmaier, M. Buess, C. H. Back, V. E. Demidov, B. Hillebrands, und S. O. Demokritov,
Spin-Waves Eigenmodes of Permalloy Squares with a Closure Domain Structure, Phys. Rev.
Lett. 94, 057202 (2005).
74
Danksagung
Am Ende möchte ich allen danken, die durch ihre Mitarbeit und Hilfe zum Gelingen dieser Diplomarbeit beigetragen haben:
Prof. Dr. B. Hillebrands für die Aufnahme in diese Arbeitsgruppe, die wissenschaftliche Betreuung
und das in mich gesetzte Vertrauen.
Prof. Dr. M. Aeschlimann für die Übernahme des Zweitgutachtens.
Prof. Dr. J. N. Chapman für die Möglichkeit in seiner Arbeitsgruppe an der Universität Glasgow
die notwendigen Untersuchungen mittels Lorentzmikroskopie durchführen zu können.
Dr. S. McVittie und Dr. N. Wiese für die technische und wissenschaftliche Unterstützung bei der
Lorentzmikroskopie.
Dr. Britta Leven für die Hilfe und Unterstützung während der Diplomarbeit.
Sebastian Hermsdörfer für die umfassende und hilfreiche Betreuung und die Einführung in die
Thematik während des letzten Jahres.
Helmut Schultheiß für die Unterstützung während der Zeit der Diplomarbeit, sowohl im wissenschaftlichen Bereich, als auch bei allen anderen Problemen, die im Rahmen dieser Diplomarbeit
auftraten.
Dr. Sandra Wolff, Dr. Bert Lägel und Christian Dautermann des Nano+Bio Centers der TU Kaiserslautern für die technische Unterstützung und die zahlreichen Tipps im Bereich der Mikrostrukturierung.
75
LITERATURVERZEICHNIS
Dr. Stefan Trellenkamp für die Unterstützung bei der Probenherstellung.
Dr. Andreas Beck für das Aufwachsen der Ni81 Fe19 -Schichten mittels Molekularstrahlepitaxie.
Sybille Müller, Bernd Pfaff, Dieter Weller und Alexander Paul für die Unterstützung bei organisatorischen und technischen Fragen.
Georg Wolf für das Korrekturlesen dieser Arbeit und die Unterstützung während des letzen Jahres.
Allen nicht namentlich genannten Mitarbeitern dieser Arbeitsgruppe für die angenehme Zusammenarbeit und die Hilfsbereitschaft.
Ganz besonders möchte ich meinen Eltern danken für die Unterstützung und das in mich gesetzte
Vertrauen während des ganzen Studiums und insbesondere während des letzten Jahres.
76