Das kognitive Modell des Menschen: Denken und Problemlösen

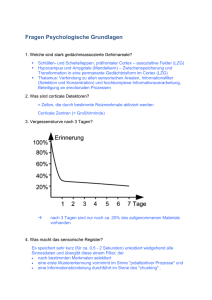
Das kognitive Modell des Menschen:
Denken und Problemlösen
PD Dr. Ralph Hansmann
1
„Cogito ergo sum“
R. Descartes (1596-1650)
Was ist das Gedächtnis?
„Ein aktives System zur Verschlüsselung
(Enkodierung), zur Speicherung und zum Abruf
und Transfer von Informationen“
(Zimbardo 1999)
2
Grundstrukturen des Gedächtnisses
1. Sensorisches Gedächtnis / sensorische
Register
2. Kurzzeitgedächtnis / Arbeitsgedächtnis
3. Langzeitlich verfügbares Gedächtnis
- Deklaratives Wissen
- Operatives / (prozedurales) Wissen
- Bewertungswissen
3
1. Sensorisches Gedächtnis / sensorisches
Register
Ø  Sinnesspezifische “Ultrakurzzeit”-Gedächtnisse (UKZG)
Ø  Ikonisches Gedächtnis (visuell), sehr grosse Kapazität,
Speicherdauer nur ca. 0.5 sec.
Ø  Echoisches/ echoartiges Gedächtnis (auditiv) bis ca. 2 sec.
Ø  Direkte Speicherung, keine eigentliche inhaltliche Verarbeitung;
Aber: selektive Übertragung ins Kurzzeitgedächtnis
Ø  Es gibt auch jeweils ein UKZG für Gerüche und den Tastsinn
-> „Jeder Sinn hat sein eigenes UKZG“
4
Experimenteller Nachweis und Speicherdauer des
ikonischen UKZG
5
Experimenteller Nachweis und Speicherdauer des
ikonischen UKZG
Teilweises berichten je einzelner Zeilen –
Signalton bestimmt Zeile
(hoher, mittlerer, tiefer Ton)
uv -> Zeit Stimulus – Signalton
Av -> Behaltensleistung
6
Experimentall variiert wurde die zeitliche
Verzögerung (= uv) des Tonsignals zur Anzeige
der Zeile nach Ausblendung der Reizvorlage ->
av = aggregierte Behaltensleistung
Beweisführung durch die Methode des teilweisen Berichtens (Sperling, 1960)
7
2. Kurzzeitgedächtnis / Arbeitsgedächtnis
§  Kapazität des Kurzzeitgedächtnis (KZG)
Ø 
Ø 
nur ca. 7 Informationseinheiten*
nur bis ca. ohne 20 Sekunden (ohne Wiederholung/ Elaboration)
§  Proaktive & retroaktive Hemmung, Spurenzerfall
§  Wie verbessert man den Transfer ins LZG?
*Miller, G. A. (1956). The magic number seven plus or minus two: Some limits on
our capacitiy for processing information. Psychological Review, 63, 81-97.
8
Bsp.
Wortlisten lernen
§ 
§ 
§ 
§ 
§ 
§ 
§ 
§ 
§ 
Esel
Maus
Fuchs
Zebra
Phönix
Nilpferd
Ziege
Schlange
Ameise
9
Was beeinflusst den Transfer vom KZG ins LZG?
§  Proaktive Hemmung: Speicherung eines Wortes interferiert mit
Speicherung/Transfer nachfolgender Worte
§  Retroaktive / retrograde Hemmung: Speicherung eines Wortes
interferiert mit Speicherung/Transfer vorheriger Worte
§  Hemmung durch ähnliches Material am grössten
Gut behalten werden:
-> Erste Elemente (keine proaktive Hemmung) -> 1, 2
-> Letzte Elemente (keine retrograde Hemmung; geringerer zeitlicher
Spurenverfall)
-> besondere Elemente (geringe Ähnlichkeit) -> 5
Prognose: - Viele erinnern ca. 7 Elemente (typische KZG-Kapazität)
- Fuchs, Zebra (3, 4), Nilpferd, Ziege (6, 7) werden weniger erinnert
10
Lernen vor dem zu Bett gehen?
-> wenige neue, nachfolgende Eindrücke
-> wenig retroaktive Hemmung -> gute Erinnerungsleistung
Weitere Strategien für besseren KZG -> LZG Transfer
§  oberflächliches Wiederholen, erhaltendes Memmorieren mit
innerer phonologischer Schleife
-> gut zur Verlängerung der Verweildauer der Information im KZG
geeignet, aber nicht sonderlich effektiv zur Verbesserung der
langzeitlichen Erinnerung
Effektiver:
§  Chunking -> Zusammenfassung zu grösseren
Informationseinheiten
§  Elaborierendes Verarbeiten -> In Bezug setzen der Information zu
Elementen des LZG -> Herstellen von „Bedeutsamkeit !!!“ der Info.
11
Bsp. 1:
Chunking (-> Zusammenfassung,“Klumpenbildung“,
Gruppierung) & elaborierendes Verarbeiten (Verknüpfung mit
LZG-Inhalten)
Wie schnell/gut können Sie sich die folgende Ziffernfolge
einprägen?
1, 9, 4, 5, 1, 9, 3, 9, 1, 9, 1, 8, 1, 9, 1,
4, 1, 8, 7, 1, 1, 8, 7, 0
12
Häufig passen jedoch die Daten nicht so gut )-:
-> aber, man kann versuchen einen Satz zu bilden.
Bsp. 2 - Chunking von „Pi“:
3,14159265358979…
Kodierung der Zahl in einem Satz:
How, I need a drink alcoholic in nature after the
heavy lectures involving quantum mechanics …
Aufgabe:
Bilde eine Satz zum Memmorieren der Eulerschen Zahl
e = 2,718
Bsp.: „Du spielst ein Haustier.“
13
3. Langzeitlich verfügbares Gedächtnis
3.1 Deklaratives Wissen
a) Semantisches Gedächtnis
Merkmalsmodell “feature model”
Vogel
Ø  hat Federn
Ø  Flügel
Ø  zwei Augen
Ø  Schnabel und
Ø  legt Eier
14
3.1 Deklaratives Wissen
a) Semantisches Gedächtnis
Semantische Netzwerke: Netzwerkmodell für Begriffs-Schemata
15
16
3.1 LZG – Deklaratives Wissen
a) Semantisches Gedächtnis
Prototypenansatz (Rosch, 1978)
-> Begriffs-Schema (z.B. für „Tasse“) durch typische Vertreter bestimmt.
-> Zuordnung zum Schema basiert auf Ähnlichkeit zum Prototyp
17
3.1 LZG - Deklaratives Wissen
b) Episodisches Gedächtnis
- autobiographische Informationen
-  Erfahrungen (“Erleben“)
-  Erlebnisse, Geschichten, in zeit- und kontextbezogener
Kodierung
-  „Skripte“ als Schemata für Ereignisse
(z.B. Skript für „Besuch in einem Restaurant)
3.2 LZG – Prozedurales Wissen
Deklarativ -> (a+b)2=a2+2ab+b2
Operativ: -> (a+b)2=(a+b)*(a+b) = aa+ab+ba+bb= a2+2ab+b2
Operativ: Auto fahren können, Ski-fahren, Lesen können, Fertigkeiten
-> Implizites, oft schwer verbal beschreibbares Wissen
18
Prozess- und Strukturmodell des Gedächtnissystems bzw.
des Denken und Problemlösens
Sensorisches
Register
[Herausfiltern von Merkmalen]
[Mustererkennung]
[Aufmerksamkeit]
Speicherung: direkte
Repräsentation
Kapazittät: gross
Dauer: kurz (visuell 0,5
sec; auditive bis zu 2
sec)
Verlust aufgrund von:
Verstreichen der Zeit,
Verdrängung durch
neues Material
Langzeitgedächtnis
(LZG)
Kurzzeitgedächtnis
(KZG)
Arbeitsgedächtnis
Bewusste
Verarbeitungsprozesse
Chunking
Erhaltendes
Wiederholen
Elaboriertes
Wiederholen
Wissenstrukturen
Prozedural
(Fertigkeiten)
Deklarativ (Fakten)
Innerer Reiz
(Gedanken)
Episodisch
Semantisch
Reaktion
Speicherung: akustisch, visuell,
semantisch
Kapazität: gering (7±2 Chunks)
Erweiterung nicht möglich,
jedoch kann der Umfang der
Chunks vergrössert werden
Dauer: vorübergehend (bis zu 20
sec) ohne Wiederholen
Verlust aufgrund von: Interferenz,
fehlendes Wiederholen, auch
Verstreichen der Zeit
Speicherung:
semantische Netzwerke (organisiert,
bedeutungstragend)
Kapazität: theoretisch unbegrenzt
Dauer: möglicherweise die ganze
Lebensspanne
Verlust aufgrund von: unangemessener
Enkodierung, Verstreichen der Zeit,
Interferenz, fehlende Konsolidierung,
motiviertes Vergessen, Misslingen des
Abrufs
19
Abb.7.7 Flussdiagramm eines hypothetischen Gedächtnissystems (Zimbardo, 1995, S. 334)
4. Problemlösen
4.1 Definition Problem:
Ein Problem ist dadurch gekennzeichnet, dass
a)  ein Ausgangszustand vorliegt, welcher
b)  in einen erwünschten Zielzustand überführt werden
soll, wobei jedoch
c)  Schwierigkeiten, Hindernisse oder Barrieren
existieren, die einer direkten und momentanen
Überführung des Ausganszustandes in den
Zielzustand im Wege stehen.
20
4.2 TOTE-Modell (Test-Operate-Test-Exit)
Modellannahme: Mensch als einfaches, intentionales, kybernetisches
Modell/Regelsystem (Miller, Galanter & Pribram, 1960)
Input
+
Test
(Ist-SollVergleich)
Exit
Operate
21
Notwendiges Wissen für TOTE
- Faktenwissen, Operatives Wissen, Bewertungswissen
Deklaratives Wissen /
Faktenwissen
Operatives Wissen /
Heuristiken / Operatoren /
prozedurales Wissen
Bewertungswissen /
evaluative Struktur
-> Wann (unter welchen Bedingungen) ist eine
Lösung gut?
-> Test ->Exit?
22
4.3 Einige Begriffe beim Problemlösen
§  Aufgabe (Oberbegriff:
nicht jede Aufgabe ist ein Problem)
§  Problem
§  Ill-defined Problem
§  Algorithmus
§  Heuristik
§  Kreatives Problemlösen
23
Aufgabe
Ausgangs- und Zielzustand
bekannt, Anwendung
bekannter
Problemlösemechanismen
geschlossenes Problem
Bekannter bzw. eindeutig
definierter Ausgangs- und
Zielzustand, zur
Problemlösung müssen
teilweise neue Methoden
entwickelt werden.
Ill-defined Problem (z.B.:
komplexe Umweltprobleme)
Ausgangszustand kann nur vage
beschrieben werden, das Ziel ist
nicht vollständig bzw. eindeutig
beschreibbar, es ist nicht klar,
welcher Typ von Barriere zu
überwinden ist.
Ausgangszustand
Zielzustand
Anwendung bekannter
Lösungsmechanismen
Zielzustand
Ausgangszustand
Barriere
Zielzustand
Ausgangszustand
Barriere
24
Algorithmus
Unter Algorithmus versteht man eine formalisierte
Regel, die sich als geordnete Sequenz von
Operationen darstellen lässt. Die Anwendung
eines Algorithmus führt bei gleichen
Eingangsformen stets zum gleichen Ergebnis
Heuristik
Unter Heuristik oder heuristischem
Lösungsverfahren versteht man solche
Vorgehensweisen, die “unsystematisch aber clever”
sind. Heuristiken (Heurismen) sind sozusagen
“Daumenregeln” (rules of thumb), die in vielen oder
gar den meisten Fällen zum gewünschten Ergebnis
führen, gelegentlich aber auch zu keiner Lösung,
oder zu einer falschen.
25
Beispiele für eine Typen von Problemen
§  Anagrammprobleme
Wie viele verschiedene Worte können aus diesen Buchstaben
gebildet werden?
G-L-A-R–E
§  Analogieprobleme
Dach : Haus = ? : Mensch
§  Reihenbildung – induktives Schlussfolgern
1.)
2, 4, 6, 8,...
2.)
13, 12, 14, 11, 15, 10, 16 ?
26
Kartenproblem
(Wason, 1960)
27
Scheckproblem (analog zu “Wason-Kartenproblem”)
Wenn ein Scheck einen Betrag über sfr. 400.- hat, muss
er auf der Rückseite eine Unterschrift besitzen.
300.-
700.-
F. Müller
Welche Karten müssen umgedreht werden, um sicher
zu wissen, ob die Regel verletzt wird?
28
Kreatives
Problemlösen
29
4.4 Tipps für kreatives Problemlösen
Ø  Beschränkung durch bzw. auf das Vorgegebene.
Ø  Über das vorgegebene Hinausgehen. – Welche Aspekte sind in der
Aufgabenstellung bzw. im Problemraum offen?
(Aufgaben A, B)
Ø  Informationsüberlastung durch irrelevante Aspekte des
Problemraums
Ø  Aufgabe C -> Streichhölzer, Faden und eine Kerze sind überflüssig
-> Element lenken von der Lösung ab
Ø  Funktionelle Gebundenheit des Denkens bzw. von Elementen
des Problemraums; Voreinstellungseffekte, (Denk)Routinen
Ø  C, D -> Streichholzschachtel als Standfläche statt Behälter;
Hammer als Pendel anstatt als Werkzeug verwenden
30
Bedeutung der kognitiven Repräsentation des
Problems bzw. Problemraums
Bsp. „Mönchsrätsel“
Ein tibetanischer Mönch bricht an einem Tag morgens im Tal auf und
erreicht Abends ein Kloster auf dem Berg. Am darauf folgenden Tag
bricht er morgens genau zur gleichen Uhrzeit auf, nimmt genau
denselben Weg wie beim Aufstieg für den Abstieg und ist dann bereits
am Nachmittag wieder im Tal.
Beweisen Sie (gegebenfalls), das er am zweiten Tag also beim
Abstieg sich an einem Punkt der Wegstrecke genau zur selben
Tages- bzw. Uhrzeit befindet wie am Tage davor beim Aufstieg.
(vgl. Zimbardo, 1996, S. 297)
31
Anstatt nur die Karten mit „A“
und „3“ umzudrehen, wählen
Leute häufig auch die Karte
„4“.
Statt die regel zu überprüfen.
Sie suchen also nach positiven
Beispielen für die Regel.
32
Lösungen: Kreatives Problemlösen
Mönchsproblem: Denken Sie an zwei Mönche, welche am selben Tag auf- bzw. absteigen,
was zur Frage analog ist. -> Das diese sich auf demselben Weg irgendwann Treffen ist klar .
33
Prinzipien von Chunking & Elaboration in Bsp. 1 und 2
Bsp. KZG/LZG 1:
1, 9, 4, 5, 1, 9, 3, 9, 1, 9, 1, 8, 1, 9, 1, 4, 1, 8, 7, 1, 1, 8, 7, 0
Chunking: Gruppierung, Aufteilung in Jahreszahlen
1945, 1939, 1918, 1914, 1871, 1870
Vertiefendes Elaborieren: Verknüpfung mit Wissen aus dem LZG ->
Jahreszahlen von Kriegsanfang, Kriegsende der drei letzten (grossen)
deutschen Kriege
Bsp. KZG/LZG 2: Anzahl Buchstaben jedes Wortes im Satz
repräsentiert die Ziffer in der entsprechenden Ziffernfolge von Pi.
-> Sätze werden in Gruppen (Bedeutungseinheiten -> Chunks) in
semantischen Netzwerken gespeichert. Sätze mit Bedeutung sind
besser im LZG speicher- und abrufbar als (scheinbar) sinnlose
Zahlenfolgen.
Danke für Ihre Aufmerksamkeit !
34