Mikroökonomie I (Märkte und Unternehmen)

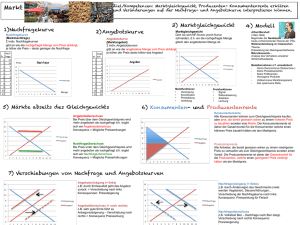
1
Mikroökonomie I
(Märkte und Unternehmen)
I. Einführung: Märkte
(Varian, Ch. 1, Ch. 15, Ch. 16)
Was ist Mikroökonomie?
Nachfrage, Angebot und Marktgleichgewicht.
II. Die Unternehmung im Wettbewerb
(Varian, Ch. 17-22)
Produktionstechnologie
Gewinnmaximierung
Faktornachfrage
Kostenminimierung
Kostenkurven
Angebotskurven
III. Marktmacht
(Varian, Ch. 23, Ch. 25, Ch. 26)
Monopol
Oligopol
Die Vorlesung orientiert sich an
Varian, H.R., Intermediate Microeconomics: A Modern
Approach, New York-London: Norton. Die in Klammern
angeführten Kapitelverweise beziehen sich auf die 3. Auflage,
1993.
(Deutsche Übersetzung: Varian, H.R., Grundzüge der
Mikroökonomik, München-Wien: Oldenbourg)
2
0. Was ist Mikroökonomie?
Mikroökonomie analysiert
− Verhalten von Wirtschaftsobjekten,
− Interaktion von Wirtschaftssubjekten
Wirtschaftssubjekte:
− Haushalte (Konsumenten)
− Firmen (Unternehmen, Produzenten)
− Ausweitung auf andere Bereiche: Politiker,
Beamte, Medien etc. (Ökonomische Theorie der
Politik, der Bürokratie etc.)
Verhalten:
− Rationalverhalten (Homo oeconomicus setzt
Mittel optimal zur Zielerreichung ein →
Entscheidungstheorie)
− alternative Ansätze: z.B. experimentelle
Ökonomie
Interaktion
− von Angebot und Nachfrage auf einzelnen
Märkten
(Partialanalyse)
− aller Wirtschaftssubjekte auf allen Märkten
(Allgemeines Gleichgewicht)
3
1. Nachfrage
Welche Menge (= wieviele Einheiten) q eines Gutes wird
gekauft (nachgefragt), wenn der Preis für eine Einheit des
Gutes p ist?
Dieser Zusammenhang wird durch die Nachfragekurve
q = D (p) (bzw. kurz q (p))
beschrieben.
Normalfall: D ′( p ) < 0
(statt D ′( p ) verwenden wir auch
dq
oder q ′( p ) ).
dp
4
Inverse Nachfragekurve (= Kurve der marginalen
Zahlungsbereitschft bzw. „Grenznutzenkurve“):
Welchen Preis p ist ein Konsument (sind Konsumenten)
für die 1., 2., ..., q-te Einheit des Gutes zu zahlen bereit?
p = P (q)
mit
(kurz p (q))
dP
( = p ′( q ) ) < 0.
dq
5
Brutto-Konsumentenrente (Gross-consumer’s surplus)
Die Summe der Zahlungsbereitschaften für q Einheiten
eines Gutes wird als Maß für die Wohlfahrt (den
„Nutzen“) verwendet, welche die Nachfrage dieser
Einheiten den Konsumenten stiftet.
Dieses Maß wird Brutto-Konsumentenrente (Grossconsumer’s surplus) genannt. Es entspricht der Fläche
unter der Nachfragekurve.
6
(Netto-) Konsumentenrente ([Net-]Consumer’s surplus)
Brutto-Konsumentenrente (Summe der Zahlungsbereitschaften) KR b ( q )
- Ausgaben für Konsum q ( = p ⋅ q )
_______________________________________________________________
= (Netto-) Konsumentenrente („Zahlungsbereitschaftsüberschuß“)
KR( q ) = KR b ( q ) − p ⋅ q
q
q
s =1
0
= ∑ p( s ) − p( q ) = ∫ [ P( s ) − p( q )]ds
7
Preiselastizität der Nachfrage
Wie sensibel reagiert die Nachfrage nach einem Gut auf
Preisänderungen?
Elastizität =
Relative (prozentuelle) Änderung der abhängigen Variable
Relative (prozentuelle) Änderung der unabhängigen Varible
ε =
dq
q
dp
dq p
=
⋅
p
dp q
(analog sind andere Elastizitäten definiert: Kreuzpreis-,
Einkommenselastizität etc. ).
Achtung: ε hängt davon ab, welcher Punkt auf der Kurve
betrachtet wird (Punktelastizität)
8
Beispiel 1: Lineare Nachfragekurve q = a - bp
Beispiel 2: Iso-elastische Nachfragekurve q = Ap −γ mit γ > 0.
9
Individuelle und aggregierte Nachfragekurve
horizontale Addition
10
2. Angebot
Welche Menge q eines Gutes wird zum Verkauf
angeboten, wenn der Preis p ist?
Dieser Zusammenhang zwischen Menge und Preis wird
durch die Angebotskurve beschrieben:
q = S ( p)
mit
S '( p )
(bzw. dq / dp ) > 0.
11
Produzentenrente (Producers’s surplus)
Die Angebotskurve kann auch in der umgekehrten
Richtung gelesen werden (inverse Angebotskurve PS ( q ) ):
Damit die q-te Einheit auf den Markt kommt, muß
mindestens der Preis p = PS ( q ) geboten werden. PS ( q )
entspricht also dem „Wert der q-ten Einheit“ für den
Anbieter. (Wir werden später zeigen, daß dieser „Wert“
den Grenzkosten der q-ten Einheit entspricht).
Erlös aus dem Verkauf von q Einheiten ( = p ⋅ q )
- Summe des „Wertes der q Einheiten“ für den Anbieter
= Produzentenrente (PR)
12
3. (Wettbewerbs)märkte
Aufeinandertreffen von Angebot und Nachfrage.
Im Wettbewerbsmarkt (man spricht auch von
polypolitischem Markt oder vollkommenem Wettbewerb)
sind Anbieter und Nachfrager Preisnehmer.
[
]
Marktgleichgewicht E = ( q ∗ , p ∗ ) : Der Preis paßt sich so
an, daß Angebot = Nachfrage, d.h.
S ( p ∗ ) = D( p ∗ ).
p ∗ ... Gleichgewichtspreis
q ∗ ... Gleichgewichtsmenge
13
Ungleichgewichte (wenn p ≠ p ∗ )
− vorübergehend (bis Preis an p∗ angepaßt)
− bei Verzerrung von Märkten durch Politik oder
Marktunvollkommenheiten
Angebotsüberschuß: S ( p' ) − D( p' ) > 0 wenn p' > p ∗ .
Beispiele:
− Politisch auferlegte Mindestpreisregelungen
( p ≥ pmin > p ∗ ) verhindern Absinken von p auf p ∗ .
− Ökonomisch bedingte Preisrigiditäten verhindern
Absinken des Preises.
(Vgl. z.B. Arbeitsmarktdiskussion).
14
Nachfrageüberschuß: S ( p' ) − D( p' ) < 0 wenn p' < p ∗ .
Beispiel: Höchstpreisregelungen ( p ≤ pmax < p ∗ ) verhindern
Anstieg von p auf p ∗ .
(Vgl. z.B. Wohnungsmarkt etc.)
15
Effizienz des Marktgleichgewichts
Bei einem vollkommenen Markt* gilt:
Sozialer Überschuß (SÜ) =
Konsumentenrente (KR) + Produzentenrente (PR)
ist im Marktgleichgewicht maximal.
*
Keine Marktmacht, keine unvollkommene Information, keine
externen Effekte!
16
Der Deadweightloss als Maß für den Wohlfahrtsverlust
infolge ineffizienter Marktergebnisse:
Bei
p'≠ p∗ gilt:
SÜ ( p' ) < SÜ ( p ∗ )
Der Verlust des sozialen Überschusses, der durch das
Abweichen von p ′ vom Gleichgewichtspreis p ∗ entsteht,
entspricht der Fläche des Dreiecks AEB.
Dieser Effizienzverlust wird oft auch deadweightloss (DWL)
genannt.
Achtung: Effizienz (SÜ) vs. Verteilung zwischen PR und
KR!
17
Komparativ-statische Analyse
Durch Änderung von
− Nachfragebedingungen (z.B. steigende Einkommen
führen zu Marktausweitung, Ersatzprodukte zu einem
Rückgang der Nachfrage)
− Angebotsbedingungen (z.B. steigende oder fallende
Inputpreise, Steuern, Subventionen)
ändert sich das Marktgleichgewicht.
Vergleicht man Marktgleichgewichte, die sich aus
verschiedenen exogenen Bedingungen ergeben, spricht
man von komparativ-statischer Analyse. (Die
dynamische Analyse der Anpassungsreaktionen auf
exogenen Änderungen wird dabei vernachlässigt).
18
Beispiel:
Kostensteigerungen
Auswirkung hängt davon ab, wie elastisch Nachfrage und
Angebot sind.
19
Beispiel: Auswirkungen einer spezifischen Mengensteuer mit
Steuersatz τ .
Steueraufkommen: τ qτ = A + B
Rückgang der Konsumentrente: A + C
Rückgang der Produzentenrente: B + D
Deadweightloss (auch Excess burden der Steuer τ
genannt): C + D