KAPAZIT¨AT und ENERGIE

Kapitel 4
KAPAZITÄT und
ENERGIE
4.1
Kondensator
Ein Kondensator besteht aus zwei Leiterplatten, die sich in einem kleinen Abstand voneinander befinden. Häufig bringt man zwischen den Elektroden eine
dielektrische Schicht ein. Diese führt zur Erhöhung1 der Kapazität.
#$ %
Beim Anlegen der Spannungsquelle im Schaltkreis (a) beobachtet man dass die Glühlampe
für einige Zeit aufleuchtet, aber dann verlischt wenn der Kondensator aufgeladen ist.
Ersetzt man die Spannungsquelle durch einen
Kurzschluss (b) beobachtet man dasselbe
Phänomen: Die Glühbirne leuchtet für einige
Zeit auf, wird schwächer und verlischt, wenn
der Kondensator entladen ist.
#& %
!
"
"
!
# $ % & '
!
!
!
!
!
! " ##$ % &$
' ((((((((()
! " ##$ % &$
' ((((((((()
Zu Beginn besteht keine Potentialdi↵erenz zwischen den Kondensatorplatten.
Deshalb erscheint beim Anlegen der Batterie die Potentialdi↵erenz U an der
Glühlampe und sie leuchtet. Der Stromfluß durch die Lampe führt zur Aufladung des Kondensators, bis die Kondensatorspannung den Wert U erreicht.
1 Mehr
dazu in Kapitel 6.
37
38
KAPITEL 4. KAPAZITÄT UND ENERGIE
Im geladenen Zustand beschreibt man den Kondensator durch zwei Elektroden, die jeweils die Ladungen +Q und Q tragen. Die beiden Elektroden befinden sich auf dem Potential 1 und 2 . Die Potentialdi↵erenz beträgt U = 1 2 .
Die Flächenladungsdichte auf den Elektroden ist = Q/A, siehe Seite 19.
Aus der Näherung (2.24) sehen wir, dass die elektrische Feldstärke im Kondensator proportional zur Ladung Q und invers proportional zur Größe der
Elektrodenoberfläche A ist,
E=
✏0
=
Q
.
✏0 A
(4.1)
Ein Kondensator hat also eine gewisse Kapazität Ladung zu tragen,
C=
Q
.
U
(4.2)
Wie viel Ladung er trägt hängt ab von der Potentialdi↵erenz U, wobei C als
Proportionalitätsfaktor erscheint, Q = C U . Mit E = U/d (d ist der Abstand
zwischen den Platten) in (4.1) und (4.1) ergibt sich für die Kapaziät eines
Plattenkondensators
C = ✏0
A
,
d
(4.3)
eine rein geometrische Abhängigkeit mit der Einheit
[Farad] = [Coulomb/Volt] .
(4.4)
Gebräuchlich sind Kondensatoren im Femto-, Pico-, Nano-, Mikro- und MillifaradBereich. Beispiel: Bei A = 1 cm2 und d = 1 mm ist C = 0.9 pF.
Feldverlauf in einem Plattenkondensator
Zwei Platten, bei x = 0 und bei x = d, tragen die Ladungen +Q und Q.
Im Raum dazwischen befinden sich keine freien Ladungen (auch keine Materie).
Zur Berechnung der Potentialverteilung verwenden wir die Laplace-Gleichung
(siehe Seite 22) in einer Dimension
d2
dx2
=0
)
(x) = ax + b
(4.5)
mit den Randbedingungen x=0 = 1 = b und x=d = 2 = ad + 1 . Mit
a=( 2
1 )/d = U/d ergibt sich der Potentialverlauf zwischen den Platten als
(x) =
U
x+
d
1
(4.6)
# $% $&
und das Feld als
~ =
E
~ =
r
U
x̂ .
d
! "!
!
(4.7)
~ =
Im Innenbereich ist das Feld homogen, |E|
das Potential steigt linear von 1 nach 2 an.
U
d,
! ""
# $% $"
"
4.1. KONDENSATOR
39
Kapazität eines Kugelkondensators
Zwei konzentrische Hohlkugeln mit den Radien ri und ra tragen die Ladungen
+Q und Q. Im Innenraum r < ri herrscht kein Feld da sich dort keine Ladungen befinden. Das Potential in diesem Bereich ist gleich dem der inneren Kugel
i
= fc Q/ri .
(4.8)
%
Das Feld zwischen beiden Kugelflächen ist
gleich dem, das eine im Kugelmittelpunkt sitzende Ladung +Q erzeugt :
~ > ri ) = fc Q êr .
E(r
r2
$
&
$
'
$
(4.9)
Das Potential für ri < r < ra ist
#"
Q
(r) = fc .
r
! "
(4.10)
Im Aussenraum (r > ra ) addiert sich das Feld der innernen Kugel (4.9) und das
der äußeren Kugel zum Gesamtfeld Null da die eingeschlossene Gesamtladung
gleich Null ist.2
Die Feldstärke macht an der Innen- bzw. Aussenwand jeweils den Sprung /✏0 ,
wobei in unserem Beispiel i = +Q/(4ri2 ⇡) und a = Q/(4ra2 ⇡) ist. Die Potentialdi↵erenz zwischen den Kugelflächen ist
✓
◆
1
1
U= i
.
(4.11)
a = fc Q
ri
ra
Mit der Definition der Kapazität eines Kondensators (4.2) ergibt sich für den
Kugelkondensator
C=
Q
=
U
Q
i
=
a
1 ri ra
.
f c ra ri
(4.12)
Wenn der Abstand zwischen den Kugelflächen klein ist (ri ⇡ R ⇡ ra ), führen wir
für den Abstand d = ra ri ein und setzen R2 ⇡ ri ra
C=
A
1 R2
4⇡✏0 R2
=
= ✏0 ,
fc d
d
d
(4.13)
wobei A = 4R2 ⇡ die Oberfläche der Kugel ist. Gleichung (4.13) entspricht also
dem eindimensionalen Fall unendlich ausgedehnter Platten, (4.3).
Kapazität einer Kugel
Wenn wir den Radius der äußeren Kugel gegen 1 anwachsen lassen, ergibt sich
aus (4.11) ein Ausdruck für die Kapazität einer einzelnen Kugel mit Radius R
gegenüber einer Gegenelektrode im Unendlichen,
C = 4⇡✏0 R .
2
(4.14)
Ob im Außenraum ein elektrisches Feld vorliegt, hängt von der Potentialdi↵erenz zwischen
der äußeren Kugel und seiner Umgebung ab. Hier ist die äussere Hohlkugel geerdet.
40
KAPITEL 4. KAPAZITÄT UND ENERGIE
Schaltung von Kondensatoren
• parallel:
Die gleiche Spannung liegt an der Summe der
Flächen, damit steigt gemäß (4.3) die Kapazität
auf
X
Cges =
Ci .
(4.15)
i
• in Serie:
Die gleiche Ladungsdi↵erenz (+Q und Q ) verteilt sich über die Summe der Abstände zwischen
den Kondensatorplatten. FürPdie gesamte anliegende Spannung gilt U0 =
i Ui . Damit sinkt
nach Gleichung (4.3) die Kapazität
X 1
1
=
.
Cges
Ci
i
(4.16)
Spannungsanstieg bei Vergrößerung des Plattenabstandes
Wir laden einen Kondensator auf, an dem ein Elektrometer angeschlossen ist.
Die Ladung verteilt sich auf Kondensator und Elektrometer gemäß ihrer Kapazität Ladungen zu tragen,
Qges = QC + QE = CE UE + CC UC = (CE + CC ) U .
Die positiv eingezeichnete Ladung Qges sei zeitlich konstant (perfekt isoliert).
Wenn wir den Plattenabstand d vergrößern beobach$
ten wir einen erhöhten Ausschlag am Elektrometer!
Beim Vergößern von d auf d0 erniedrigt sich die Ka0
pazität von CC = ✏0 A/d auf CC
= ✏0 A/d0 . Weil
UC = UE = U ist gilt bei konstanter Ladung Q,
!
Qges
U0
U
=
=
!
"
0
(CE + CC ) U = (CE + CC
) U0 ,
✓
◆
d 0 d CE + ✏ 0 A
.
d d0 C E + ✏ 0 A
#
Der Ausdruck in Klammer ist Eins wenn die Kapazität des Elektrometers sehr
viel kleiner ist als die des Kondensators. In diesem Fall gilt U/d ⇡ U 0 /d0 und man
dürfte argumentieren, dass das Feld im Kondensator konstant bleibt, E=U/d.
Das ist konsistent mit der Annahme, dass die Ladung am Kondensator QC
gleich bleibt denn E = ✏0QA . Damit bleibt aber QE gleich, das Elektrometer
hätte keinen Grund weiter auszuschlagen...
$
Genauer lässt sich im Bild rechts argumentieren. Der Kondensator liegt an einer festen Spannungsquelle, U0 . Bei Vergößerung
von d sinkt C und Q, weil Ladung in die !
Quelle und Erdung abfließen kann. Wenn
im Bild links d erhöht wird, dann sinkt C.
Weil Q erhalten bleibt steigt Uc an.
$
$
+
"
!
#
!
"
!
!
#
U" 0
-
!U0#
41
4.2
Energie des elektrischen Feldes
!
Ein Ladungslö↵el überträgt die Ladungsmenge dQ auf eine isolierte Kugel im Vakuum und
leistet dabei die Arbeit
! "
dW = dQ (
#
wobei wir
Für das Potential der Kugel schreiben wir
W = fc
1
R
Z
Q dQ =
R
1
R
1)
= dQ
R
= 0 gesetzt haben.
= fc Q
R . Die Arbeit ist also gleich
1
Q2
1 Q2
·
=
4⇡✏0 R 2
2 C
(4.17)
Eine geladene Kugel ist damit ein Energiespeicher
Wel =
1 Q2
1
1
= CU 2 = Q U .
2 C
2
2
Diese Gleichung verwenden wir jetzt für einen
ebenen Plattenkondensator. Für ihn gelten die
Beziehungen
C
=
✏0 A/d ,
U
=
E d.
(4.18)
"
!
Das Volumen des Kondensators ist V = A d. Die
in diesem Volumen im elektrischen Feld gespeicherte Energie ist daher
Wel =
1
1
1
C U 2 = ✏0 E 2 A d = ✏0 E 2 V .
2
2
2
(4.19)
Diese Beziehung gilt für beliebige elektrische Feldanordnungen im Vakuum.
Über sie definiert sich die Energiedichte des elektrischen Feldes,
wel =
Wel
1
= ✏0 E 2 .
V
2
(4.20)
Die physikalischen Einheiten der Energiedichte des elektrischen Feldes sind


1
A · s V2
V·A·s
W·s
J
2
[wel ] =
✏0 E =
=
=
=
.
(4.21)
2
V · m m2
m3
m3
m3
Kondensator als Speicher
Bei Ladungsentnahme sinkt die Spannung am Kondensator. Deshalb eignet er
sich i.A. nicht als Ersatz für Batterien. Ein Bleiakku bringt etwa 100 kJ/kg
(das entspricht etwa 30 Wh/kg). Eine Alkali Batterie bringt bis zu 600 kJ/kg.
Konventionelle Kondensatoren liegen bei 0.3 kJ/kg.
Trotzdem finden Kondensatoren vielfache Anwendung als Leistungsspeicher:
Bei der Elektroschocktheraphie braucht man einige hundert J die in 2 ms dem
Patienten in die Brust deponiert werden (200 J in 2 ms entspricht 100 kW).
42
Ebenso bei Blitzlampen oder Netzgeräten für gepulste Laser. Eine Batterie wäre
überfordert, da die chemischen Reaktionen nicht schnell genug sind.
Ein wichtige Anwendung von vielen sehr kleinen Kondensatoren (⇡ femtoF)
ist ihr Einsatz in Datenspeichern. (1 fF bei 1 V entspricht ⇡ 6⇥104 Elektronen).
Kraft zwischen Platten eines Kondensators
Das elektrische Feld zwischen den Platten eines Kondensators beträgt
E=
✏0
=
Q
,
✏0 A
(4.22)
wobei A die Plattenfläche angibt. Die elektrische Feldstärke ist unabhängig vom
Abstand der Platten (siehe Seite 19). Da die Platten entgegengesetzt geladen
sind (+Q und Q) ziehen sie sich mit einer Kraft F an.
Vergrößern wir den Plattenabstand d um einen Betrag d, dann leisten wir
die Arbeit F · d. Dieser Arbeit entspricht eine Zunahme der elektrostatischen
Feldenergie um 12 ✏0 E 2 · A · d. Damit ergibt sich für die Kraft zwischen beiden
Platten
F =
1
1
✏0 E 2 A = Q E ,
2
2
(4.23)
wobei wir E = Q/(✏0 A) verwendet haben. Der Faktor 1/2 gegenüber dem Ausdruck (2.8) ist folgendermaßen einzusehen: Ausserhalb der Kondensatorplatten
ist das elektrische Feld gleich Null. Die Feldstärke fällt also über die endliche
Dicke der Ladungsschicht auf der Kondensatorplatte auf Null ab, sodass auf die
Ladungen im Mittel nur das Feld E/2 wirkt.
Sicherheitsaspekte
Die Gefährlichkeit eines Stromschlages ist durch die Größe des Stromes bestimmt. Kleine Ströme (< 5 mA) spürt man als unangenehm, sie führen aber zu
keinem dauerhaften Schaden. Ströme > 50 mA führen zu Schäden, da sie Nervensignale übertre↵en und Muskelbewegungen (Herz) einfrieren können. Tri↵t
dies für mehrere Sekunden zu, kann dies zum Tod führen. Der typische Innenwiderstand des menschlichen Körpers liegt im Bereich von einigen 100 ⌦. Damit ist die Spannungsgrenze für gefährliche Stromschläge im Bereich von
U = I R = 0.05⇥100 = 5 Volt ! Das bedeutet, dass im Prinzip eine Autobatterie
für einen tödlichen Stromschlag ausreicht. Auf Grund des hohen Widerstandes
trockener Haut (⇡ 20 k⌦) liegt aber die gefährliche Grenze erheblich höher. Aus
diesem Grund überlebt man typisch den Stromschlag aus dem Netz (es sei denn,
man sitzt in der Badewanne).
Ein weiterer Gesichtspunkt ist die Leistung der Stromquelle. Eine 1 kV
Überlandleitung kann über lange Zeit sehr große Ströme abführen und ist damit
tödlich. Ein Van-de-Gra↵ Generator scha↵t mehrere 100 kV, kann aber nur
Strom für sehr kurze Zeit liefern. Dasselbe gilt für eine Tesla-Spule die mehrere
106 V liefert, aber im Normalfall keine großen Ströme. Beim Gehen auf einem
isolierten Teppich kann sich der Körper auf mehrere Tausend Volt aufladen und mit einem entsprechenden Blitz (z.B. bei Berührung mit einem geerdeten
Stiegengeländer) entladen, ohne dass großer Schaden entsteht.
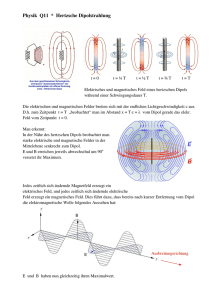
Kapitel 5
ELEKTRISCHER DIPOL
Wegen der Linearität der Poisson Gleichung,
onsprinzip,
~ = fc
(R)
X
i
Qi
~
|R
~ri |
.
=
⇢/✏0 gilt das Superpositi-
(5.1)
! "$ %
&
! #"
Für Ladungen, die im Raum kontinuierlich
verteilt sind gilt
Z
⇢(~r) dV
~
(R) = fc
.
(5.2)
~ ~r|
V |R
'(
"
!
Die Potentialgleichung (5.2) ist allerdings nur in Spezialfällen analytisch lösbar.
~ weit entfernt von der Ladungsverteilung,
Interessiert man sich für Aufpunkte R
dann bewährt sich die sogenannte Multipolentwicklung, eine Taylorentwick~ ~r| um ~r = 0. Der Gedanke dahinter ist folgender: weit
lung des Terms 1/|R
entfernt von der Ladungsverteilung, ist das Potential die Summe einfacher
Verteilungen positiver und negativer Ladungen.
Diese beschreiben das Potential eines Monopols (Punktladung), Dipols
(Punktladungspaar), Quadrupols (Dipolpaar), Oktopol (Quadupolpaar). . . .
Der elektrische Dipol besteht aus zwei entgegengesetzt gleichen Ladungen Q im Abstand d. Das elektrische Dipolmoment ist definiert als
p~ = Q d~
!
'$ ()
& '%
&
" #
(5.3)
Aus der Überlagerung des Potentialfeldes der
beiden Punktladungen ergibt sich das Dipolpotential
43
!
$
%#
"
& '
'$
()
44
KAPITEL 5. ELEKTRISCHER DIPOL
dipol
= fc Q
1
~
|R
1
~
d/2|
~
~ + d/2|
|R
!
(5.4)
~ von den
~ ± d/2
wobei die Vektoren R
entsprechenen Ladungen zum Aufpunkt zeigen.
Das Bild zeigt den Potentialverlauf
(die potentielle Energie einer Einheitsladung) in der Umgebung der
beiden Ladungen ±Q die in der x y
Ebene liegen.
In einer Reihen-Entwicklung für
R
d erhalten wir
1
1
1
q
=
~
~ ± d/2|
~
~ d
R
R·
|R
1 ± R2 +
d2
4R2
1
1
q
⇡
R
1±
~
~ d
R·
R2
1
⇡
R
~ · d~
1R
1⌥
± ....
2 R2
!
Einsetzen in (5.4) und Einführung des Polarwinkels ✓ (Seite 43) ergibt die für
|R|
|d| gültige Näherungslösung,
dipol
= fc Q
~ · d~
~ · p~
R
R
p cos✓
= fc 3 = fc
.
3
R
R
R2
(5.5)
In großer Entfernung (|R|
|d|) nimmt das Dipolpotential mit 1/R2 ab. Im
Vergleich dazu nimmt das Potential des Monopols (2.40) mit 1/R ab, das des
Quadrupols mit 1/R3 . Je höher die Ordnung des Multipols, je geringer ist die
Reichweite des Potentials.
Die obere Reihe gibt die
exakte
Potentialverteilung
(5.4) im Nahfeld und im
Fernfeld. Die untere Reihe
zeigt die Näherung (5.5).
Die beiden Ladungen befinden sich bei x = y = 0, z = ±1.
Weit von diesen Positionen
sind die Lösungen (5.4) und
(5.5) nahezu identisch (rechte
Spalte).
Das Bild unten links zeigt das
Versagen der Näherung (5.5)
bei kleinen Abständen.
~ = r
~ aus der Näherung (5.5)
Zur Berechnung der elektrischen Feldstärke E
benötigen wir den Nabla Operator in Kugelkoordinaten.
45
Nabla Operator in Kugelkoordinaten
Zur Berechnung des Feldstärkeverlaufs aus Gleichung 5.5 brauchen wir den Nabla Operator in Kugelkoordinaten (sphärischen Koordinaten). In kartesischen
Koordinaten haben wir für den Nabla Operator
⇢
~ = êx @ , êy @ , êz @
r
.
(5.6)
@x
@y
@z
Also jeweils das Produkt aus Einheitsvektor mal der Änderung bei einem infinitesimalen Schritt in Richtung des Einheitsvektors. In einer beliebigen orthonormalen Basis gilt: ê1 ⇥ ê2 = ê3 , ê2 ⇥ ê3 = ê1 , ê3 ⇥ ê1 = ê2 . Die Einheitsvektoren
für Kugelkoordinaten sind in kartesischer Basis:
êR
=
{ sin ✓ cos ', sin ✓ sin ', cos ✓ }
ê✓
=
{ cos ✓ cos ', cos ✓ sin ',
ê'
=
{
sin ', cos ', 0 }
sin ✓ }
radial
(5.7)
tangential an
Längenkreis
(5.8)
(5.9)
tangential an Breitenkreis
Der Winkel ✓ is Null am Nordpol und erreicht ✓ = ⇡/2 am Äquator. ' läuft im
Uhrzeigersinn von 0 ! 2⇡, wenn wir in Richtung der z Achse schauen. Den Differentialoperator in Kugelkoordinaten erhalten wir indem wir uns infinitesimale
Reisen auf einer (Erd)Kugel überlegen:
• nach Osten ändert sich nur ',
unser Weg ist R sin ✓ d'
• nach Süden ändert sich nur ✓,
unser Weg ist R d✓
R sin q dj
z
R dq
q
Damit wird Nabla in sphärischen Koordinaten:
⇢
@
1 @
1
@
~
r = êR
, ê✓
, ê'
.
@R
R @✓
R sin ✓ @'
dR
R dq
z
dq
dq
q
y
y
• nach Oben ändert sich nur R,
unser Weg ist dR
R sin q dj
dR
dj
dj
j
j
x
x
(5.10)
Mit diesem Ausdruck berechnen wir die Feldstärke in Kugelkoordinaten:
⇢
@ 1 @
1
@
~
~
E = r dipol =
,
,
(5.11)
dipol .
@R R @✓ R sin ✓ @'
Die Dipolachse liegt entlang der z-Achse (~
p || ~z ), siehe Seite 43. Für das Fernfeld
des Dipols ergibt sich aus (5.11) mit (5.5) ein um z rotationssymmetrisches Feld
mit den Feldkomponenten
ER
=
E✓
=
E'
=
2 p cos✓
,
R3
p sin✓
fc
,
R3
fc
0.
(5.12)
(5.13)
(5.14)
46
KAPITEL 5. ELEKTRISCHER DIPOL
Potentielle Energie des Dipols im externen Feld
Ein äußeres elektrisches Feld sei durch die Potentialwerte 1 und 2 an den Orten der beiden Dipolladungen charakterisiert. Die potentielle Energie des Dipols in diesem Feld ist
Wpot
=
=
=
Q( 1
~
Q d~ · r
2)
#
$
~
p~ · E
(5.15)
!
~ liegt.
Wpot ist Null, wenn p~ ? E
~
Wpot ist ein Minimum für p~ || E.
~
Wpot ist ein Maximum für p~ || E.
!
!
"
Kräfte auf einen Dipol im externen Feld
Im Feld sind die Kräfte auf die Einzelladungen
~ 1 und F~2 = Q E
~ 2.
des Dipols F~1 = +Q E
!
Im homogenen Feld sind die Feldstärken
~1 = E
~ 2 = E,
~ die resultierende Kraft ist
gleich, E
gleich Null, aber ein Drehmoment wirkt auf
den Dipol
$
~ = p~ ⇥ E
~.
D
#
!
"
Im inhomogenen Feld ist die resultierende
Kraft
h
i
~
~
~ r + d)
~ r) = p~ dE
F~1 + F~2 = Q E(~
E(~
d~r
!
wobei
&
Fx
=
Fy
=
Fz
=
⇥
⇤
Q Ex+ Ex = p~ · grad Ex
⇤
⇥
Q Ey+ Ey = p~ · grad Ey
⇥
⇤
Q Ez+ Ez = p~ · grad Ez
!
$
#
"
%
~ r den Vektorgradienten dar. Im inhomogenen Feld erfährt
Dabei stellt dE/d~
der Dipol ein Drehmoment und eine Kraft in Richtung wachsender Feldstärke,
Fx
=
Fy
=
Fz
=
p
~ · grad Ex = px (@x Ex ) + py (@y Ex ) + pz (@z Ex ) ,
p
~ · grad Ey = px (@x Ey ) + py (@y Ey ) + pz (@z Ey ) ,
p
~ · grad Ez = px (@x Ez ) + py (@y Ez ) + pz (@z Ez ) .
5.1. MOLEKULARE UND ATOMARE DIPOLMOMENTE
47
Elektrischer Quadrupol
Vier Monopole mit der Gesamtladung Null
stellt man als eine Überlagerung zweier Dipole
dar
#
~ + ~a/2)
= dipol (R
~
dipol (R
~a/2) .
Multipol-Beiträge wie Dipol, Quadrupol und
höherer Ordnung verwendet man als Maß für
die Abweichung einer Ladungsverteilung von
der Kugelsymmetrie.
5.1
!
!
"
Molekulare und atomare Dipolmomente
Moleküle mit permanentem Dipolmoment, z.B.
OH oder H2 O werden im Feld ausgerichtet. Dabei entsteht eine makroskopische Polarisation
(Orientierungspolarisation). Anwendung z.B.
im gezielten Aussortieren von Wassertröpfchen.
(mit Farbsto↵ markierte Zellen, Chromosome, ..
sind optisch erkennbar, stark verdünnt, auf einzelne Tropfen verteilt).
Unpolare Moleküle, z.B. CO2 im Grundzustand oder Atome tragen kein permanentes Dipolmoment. Ein äußeres Feld induziert in ihnen ein Dipolmoment.
Zum Beispiel beobachtet man in einem O-Atom, das einem Proton begegnet
ein induziertes Dipolmoment. Die Kraftwirkung des Feldes von H+ mit dem
induzierten Dipolmoment im neutralen Sauersto↵ Atom ist z.B. durch die Bahnablenkung des Protons beobachtbar. Das induzierte Dipolmoment skaliert mit
1/r2 , wobei r der Abstand zwischen Proton und O-Atom ist.
+
+—
+
+—
+
+—
.
Das induzierte Dipolmoment p~ in einem einzelnen Atom beschreibt man über
die Polarisierbarkeit ↵ mit
~.
p~ = ↵ E
(5.16)
Die Polarisierbarkeit ist klein für Edelgase, hingegen groß für Alkali Atome.
Liegt das Feld entlang z, dann wandern die Ladungsschwerpunkte der positiven Kern~
ladungen und der Elektronenhülle um den Betrag |~z | auseinander, p
~ = q ~z = ↵ E.
Die Wechselwirkungsenergie des induzierten Dipols im Feld des Protons ist gemäß
~ Da p
~ ergibt sich für die potentielle Energie der
Gl. (5.15) gleich V (r) = p
~ · E.
~ ||E
Wechselwirkung zwischen einer Punktladung und einem polarisierbaren Atom (Molekül) der Ausdruck V (r) / ↵/r4 , das sogenannte Langevin-Potential.
48
KAPITEL 5. ELEKTRISCHER DIPOL
5.2
Methode der Bildladungen
Wir betrachten die exakte Feldverteilung
in der unmittelbaren Umgebung eines Dipols (2 Punktladungen mit q1 =
q2 ).
Die Äquipotentialflächen sind strichliert eingezeichnet. Im Fall des Dipols sind die
Äquipotentialflächen gestauchte Ellispoide,
spiegelsymmetrisch um die Ebene senkrecht
zur Verbindungslinie zwischen den beiden Ladungen.
Wir wählen eine dieser Äquipotentialflächen
aus und belegen sie (gedanklich) mit einer
dünnen, leitenden Schicht. Damit ändert sich
nichts an der Feldlinienverteilung!
+
-
Mit dieser Überlegung haben wir ein neues Problem der Elektrostatik gelöst:
Wie ist der Feldverlauf zwischen einer Punktladung und einer leitenden Schicht
in der Form einer Äquipotentialfläche des Dipols?
Rechts (oder links) von der leitenden Fläche können wir das Volumen mit einem Leiter oder Isolator füllen, es ändert nichts an der Verteilung des Feldes im
linken (bzw. rechten) Raum. Das folgende Bild zeigt zwei solche Anordnungen.
Einmal erhalten wir so das Feld zwischen einer Punktladung und einer ebenen
Leiterfläche (linkes Bild). Im rechten Bild erhalten wir das Feld zwischen einer
Punktladung und der blau eingezeichneten ellipsoiden Oberfläche.
+
-
+
-
Das Feld ist so, als ob eine Bildladung entgegengesetzten Vorzeichens
hinter der Leiterfläche läge, in einem Abstand, so dass die Feldlinien
senkrecht in die Leiteroberfläche münden.
~
Warum verschwindet im statischen Fall die Tangentialkomponente des E-Feldes
an der Oberfläche des Leiters? ! Sonst würde ein Strom fließen, bis sich die
Ladungen im Leiter so verteilen, dass die Tangentialkomponente verschwindet.