Resolution

Logik und Diskrete Strukturen (Sommer 2017)
Prof. Dr. Ulrich Hertrampf
Resolution
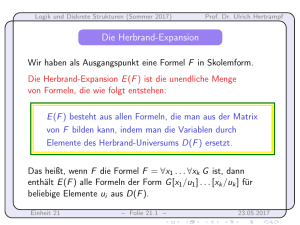
Grundlage ist immer eine prädikatenlogische Formel in Skolemform.
Wir definieren Grundsubstitutionen, Instanzen, Grundinstanzen:
Eine Grundsubstitution ist eine Substitution, bei der jede
Variable von F durch einen variablenfreien Term ersetzt
wird. (Es ergibt sich dabei ein Element von E (F ).)
Wenn man in der Formel F jede Variable durch einen beliebigen
Term ersetzt, spricht man von einer Instanz der Formel F .
Entsteht die Instanz G aus F durch eine Grundsubstitution,
so nennt man G eine Grundinstanz der Formel F .
Beispiel: F = P(x) ∧ ¬P(f (x))
Die folgende Instanz ist keine Grundinstanz von F : P(f (x)) ∧ ¬P(f (f (x)))
Aber diese Instanz ist eine Grundinstanz von F : P(f (a)) ∧ ¬P(f (f (a)))
Einheit 22
– Folie 22.1 –
30.05.2017
Logik und Diskrete Strukturen (Sommer 2017)
Prof. Dr. Ulrich Hertrampf
Grundresolution
Wir gehen wieder von einer Aussage in Skolemform aus:
F = ∀x1 ∀x2 . . . ∀xk G
Der folgende sogenannte Grundresolutionsalgorithmus benutzt
eine Aufzählung von E (F ) in der Form {F1 , F2 , F3 , . . . }:
i := 0;
M := ∅;
repeat i := i + 1;
M := M ∪ {Fi };
M := Res ∗ (M);
until ∈ M;
output(„unerfüllbar“);
Einheit 22
– Folie 22.2 –
30.05.2017
Logik und Diskrete Strukturen (Sommer 2017)
Prof. Dr. Ulrich Hertrampf
Korrektheit und Beispiel
Der eben angegebene Grundresolutionsalgorithmus ist eine
Variante des Algorithmus von Gilmore (sh. Buch). Folgender
Satz ist leicht zu beweisen:
Satz: Der Grundresolutionsalgorithmus stoppt (und
gibt „unerfüllbar“ aus) genau dann, wenn die
Formel F unerfüllbar ist.
Als erstes Beispiel betrachten wir
F = ∀x (P(x) ∧ ¬P(f (x)))
Wir erhalten D(F ) = {a, f (a), f (f (a)), . . . } und damit für die Matrix (P(x) ∧ ¬P(f (x)))
die Elemente G1 = (P(a) ∧ ¬P(f (a))) und G2 = (P(f (a)) ∧ ¬P(f (f (a)))) von E (F ).
Die Klauseln P(f (a)) und ¬P(f (a)) können zur leeren Klausel resolviert werden.
30.05.2017
Einheit 22
– Folie 22.3 –
Logik und Diskrete Strukturen (Sommer 2017)
Prof. Dr. Ulrich Hertrampf
Noch ein Beispiel
Das folgende Beispiel ist etwas komplizierter als das vorige:
F = ∀x∀y ((¬P(x) ∨ ¬P(f (a)) ∨ Q(y )) ∧ P(y ) ∧ (¬P(g (b, x)) ∨ ¬Q(b)))
Die Matrix ist
G = (¬P(x) ∨ ¬P(f (a)) ∨ Q(y )) ∧ P(y ) ∧ (¬P(g (b, x)) ∨ ¬Q(b))
Wir betrachten vier Elemente von E (F ) (also Grundinstanzen):
G [x/f (a)][y /b]
Hier finden wir die Klausel (¬P(f (a)) ∨ Q(b)).
G [y /f (a)]
Hier finden wir die Klausel P(f (a)).
G [y /g (b, a)]
Hier finden wir die Klausel P(g (b, a)).
G [x/a]
Hier finden wir die Klausel (¬P(g (b, a)) ∨ ¬Q(b)).
Einheit 22
– Folie 22.4 –
30.05.2017
Logik und Diskrete Strukturen (Sommer 2017)
Prof. Dr. Ulrich Hertrampf
Herleitungen
Wir betrachten die Klauseln aus den Grundinstanzen analog
zu unserem Vorgehen bei der aussagenlogischen Resolution.
Auch hier können wir eine Herleitung der leeren Klausel finden,
ohne den ganzen Resolutionsabschluss zu konstruieren:
¬P(f (a)) ∨ Q(b)
P(f (a))
P(g (b, a))
¬P(g (b, a)) ∨ ¬Q(b)
¬Q(b)
Q(b)
Einheit 22
– Folie 22.5 –
30.05.2017
Logik und Diskrete Strukturen (Sommer 2017)
Prof. Dr. Ulrich Hertrampf
Grundresolutionssatz
Eine Formalisierung des Vorgehens beim letzten Beispiel führt
zu dem folgenden Satz, den man Grundresolutionssatz nennt:
Satz: Sei F = ∀y1 ∀y2 . . . ∀yk G eine Aussage in Skolemform,
wobei die Matrix G in KNF vorliegt. F ist unerfüllbar
genau dann, wenn es eine Folge K1 , . . . , Kn von
Klauseln gibt, so dass
1) Kn = und
2) für alle i ist Ki entweder Grundinstanz einer
Klausel aus G oder Resolvent zweier Klauseln
Ka und Kb mit a < b < i.
Einheit 22
– Folie 22.6 –
30.05.2017