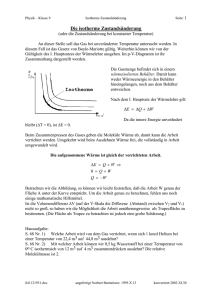
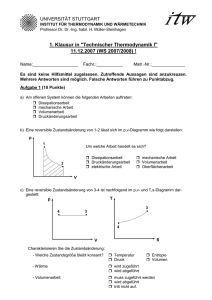
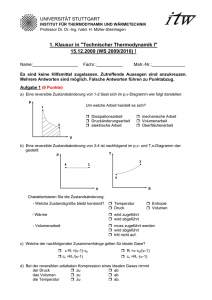
∫ ( )
Werbung

5. Anwendungen des ersten und zweiten Hauptsatzes 5.1 Volumenänderungsarbeit und Druckänderungsarbeit bei änderungen in geschlossenen und offenen Systemen Zustands- In den vorangegangenen Kapiteln haben wir uns mit dem Handwerkszeug zur Berechnung von thermodynamischen Prozessen in geschlossenen und offenen Systemen befasst. Insbesondere haben wir den ersten und zweiten Hauptsatz der Thermodynamik in den Schreibweisen für geschlossene Systeme und für stationäre Fließprozesse kennen gelernt. Mit Hilfe der Energiebilanzgleichungen des ersten Hauptsatzes lassen sich die bei einem Prozess relevanten energetischen Größen — z. B. die zu- oder abzuführende spezifische Wärme q12, die spezifische Volumenänderungsarbeit beim geschlossenen System oder die spezifische technische Arbeit beim stationären Fließprozess — berechnen. Dies geht jedoch nur, wenn im Falle des geschlossenen Systems die spezifische Volumenänderungsarbeit wV12 und im Falle des stationären Fließprozesses die spezifische Druckänderungsarbeit wP12 bekannt ist. Diese Prozessgrößen müssen zuvor durch Lösung der vom Integrationsweg abhängigen Integrale 2 w V12 = − ∫ p( v )dv (Gl. 5.1) 1 2 w P12 = ∫ v( p )dp (Gl. 5.2) 1 berechnet werden. Dies ist wiederum nur möglich, wenn die Funktionen p(v) bzw. v(p) explizit angegeben werden können. Abb. 5.1 zeigt die Integrale der Gln. 5.1 a, b im p,v-Diagramm: Abb. 5.1: Volumenänderungsarbeit und Druckänderungsarbeit im p,v-Diagramm 85 An einem p,v- oder T,s-Diagramm lässt sich nicht erkennen, ob die darin dargestellte Zustandsänderung in einem geschlossenen System oder als stationärer Fließprozess abläuft. Da derselbe Zustandsverlauf — wie im p,v-Diagramm der Abb. 5.1 zu ersehen ist — sowohl durch eine Funktionen p(v) als auch durch eine Funktion v(p) beschrieben werden kann, besteht zwischen den beiden Integralen vdp und pdv der folgende Zusammenhang: 2 2 1 1 ∫ v dp = − ∫ p dv + p2 v 2 − p1 v1 (Gl. 5.3) Gl. 5.3 ist gültig für Prozesse in geschlossenen und offenen Systemen. Auf Folgendes sei in diesem Zusammenhang jedoch besonders hingewiesen: Auch bei einem geschlossenen System kann rein formal das Integral vdp berechnet werden. Es stellt aber nicht wie beim Fließprozess eine Druckänderungsarbeit dar. Es ist eine reine Rechengröße (vgl. Cerbe, Hoffmann, 1994, S. 47). Dieser Sachverhalt lässt sich leicht an einem isochoren Prozess in einem geschlossenen System klarmachen: Wenn in einem Behälter mit starren Systemgrenzen durch Wärmezufuhr der Druck steigt, wird deswegen keine Druckänderungsarbeit verrichtet. Trotzdem existiert für einen solchen Prozess das Integral vdp als Rechengröße. Die für geschlossene Systeme besonders wichtige Volumenänderungsarbeit kommt auch bei offenen Systemen vor. Im Falle eines Fließprozesses nimmt Gl. 5.3 die Form von Gl. 3.50 an. Es gilt dann: w P 12 = w V 12 + p2 v 2 − p1 v1 (Gl. 3.50) Bei Fließprozessen ist die Volumenänderungsarbeit von untergeordnetem Interesse, weil sie lediglich ein Bestandteil der Druckänderungsarbeit ist. Die Druckänderungsarbeit stellt bei einem stationären Fließprozess die für die Energiebilanz maßgebliche Arbeit dar. Das sieht man daran, dass bei einem Fließprozess einer inkompressiblen Flüssigkeit bei Druckverminderung Druckänderungsarbeit abgegeben wird, jedoch aufgrund der Inkompressibilität keine Volumenänderung und damit auch keine Volumenänderungsarbeit auftritt (vgl. Baehr, 1973, S.76). 86 5.2 Isochore Zustandsänderung Bei einer isochoren Zustandsänderung bleibt unabhängig davon, ob der Prozess in einem geschlossenen oder offenen System abläuft, das spezifische Volumen v und damit die Dichte ρ des Fluids konstant. Im p,v-Diagramm verläuft die Zustandsänderungslinie senkrecht. Den Verlauf im T,sDiagramm kann man nur dann angeben, wenn man die thermische Zustandsgleichung des Mediums kennt, das die Zustandsänderung durchmacht. Für ideale Gase verläuft eine isochore Zustandsänderung im T,s-Diagramm als Exponentialfunktion. Abb. 5.2: Isochore Zustandsänderung (1) → (2) eines idealen Gases im p,vund im T,s-Diagramm (vgl. Langeheinecke et al., 1999, S.140) Abb. 5.2 zeigt die isochore Zustandsänderung eines idealen Gases im p,v- und im T,s-Diagramm. Im p,v-Diagramm stellt die Fläche zwischen der Isochoren und der Ordinate das Integral vdp dar, das im Falle eines Fließprozesses mit der spezifischen Druckänderungsarbeit wP12 identisch ist. Im T,s-Diagramm ist die Fläche zwischen der Isochoren und der Abszisse die Summe aus übertragener spezifischer Wärme und zugeführter spezifischer Dissipationsenergie, q12 + j12. Des Weiteren stellt sie die Differenz der spezifischen inneren Energie u2 - u1 dar. Geschlossenes System Eine isochore Zustandsänderung in einem geschlossenen System liegt vor, wenn ein Prozess in einem Behälter mit starren Wänden abläuft. Für das in dem Behälter eingeschlossene Medium gelten diesen Fall die folgenden Beziehungen: Thermische Zustandsgleichung: V = konst. bzw. v, ρ = konst. (Gl. 5.4) 87 Spezifische Volumenänderungsarbeit: 2 w V 12 = − ∫ p dv = 0 (Gl. 5.5) 1 1. HS für geschlossene Systeme: q12 + j12 = u2 − u1 (Gl. 5.6) Bei einer isochoren Zustandsänderung nimmt durch Zufuhr von Wärme oder Dissipationsenergie die innere Energie, und damit die Temperatur zu. Die Gln. 5.4 bis 5.6 sind allgemeingültig, d. h., sie sind an kein spezielles Stoffmodell geknüpft. Möchte man jedoch die Differenz der spezifischen inneren Energie mit einer Temperaturdifferenz in Verbindung bringen, so muss das über die kalorische Zustandsgleichung des betreffenden Mediums geschehen. Der kalorischen Zustandsgleichung liegen jedoch spezielle Stoffmodelle wie das des idealen Gases oder der idealen Flüssigkeit zugrunde, siehe Kap. 3.4. Stationärer Fließprozess Bei einem stationären Fließprozess ist bei isochorer Zustandsänderung der Volumenstrom in allen Strömungsquerschnitten des Kontrollraums konstant. Dies ist bei stationären Fließprozessen nur bei idealen Flüssigkeiten der Fall. Hierfür gelten die folgenden Beziehungen: Thermische Zustandsgleichung: • V = konst. v, ρ = konst. bzw. (Gl. 5.7) Kalorische Zustandsgleichung für ideale Flüssigkeit (Gln. 3.70, 3.71): h2 − h1 = u2 − u1 + u2 − u1 mit 1 ρ ⋅ ( p 2 − p1 ) = c F ⋅ (T2 − T1 ) (Gl. 5.8) (Gl. 5.9) Spezifische Druckänderungsarbeit: 2 w P12 = ∫ v dp 1 = 1 ρ ⋅ ( p 2 − p1 ) (Gl. 5.10) 88 1. HS für stationäre Fließprozesse: q12 + w t 12 = h2 − h1 + ( ) ( 1 2 2 ⋅ c 2 − c1 + g ⋅ z 2 − z1 2 ) (Gl. 5.11) Spezifische technische Arbeit: w t 12 = j12 + 1 ρ ⋅ ( p 2 − p1 ) + ( ) ( 1 2 2 ⋅ c 2 − c1 + g ⋅ z 2 − z1 2 ) (Gl. 5.12) Gl. 5.12 ist identisch mit der aus der Strömungsmechanik bekannten erweiterten Form der Gleichung von BERNOULLI. 5.3 Isobare Zustandsänderung Bei einer isobaren Zustandsänderung bleibt unabhängig davon, ob der Prozess in einem geschlossenen oder offenen System stattfindet, der Druck konstant. Im p,vDiagramm verläuft die Zustandsänderungslinie waagerecht. Den Verlauf im T,sDiagramm kann man nur dann angeben, wenn man die thermische Zustandsgleichung des Mediums kennt. Für ideale Gase verläuft eine isobare Zustandsänderung im T,s-Diagramm als Exponentialfunktion. Abb. 5.3: Isobare Zustandsänderung (1) → (2) eines idealen Gases im p,vund im T,s-Diagramm (vgl. Langeheinecke et al., 1999, S. 137) Abb. 5.3 zeigt die isobare Zustandsänderung eines idealen Gases im p,v- und im T,s-Diagramm. Im p,v-Diagramm stellt die Fläche zwischen der Isobaren und der Abszisse die negative spezifische Volumenänderungsarbeit −wV12 dar. Im T,sDiagramm ist die Fläche zwischen der Isobaren und der Abszisse die Summe aus übertragener spezifischer Wärme und zugeführter spezifischer Dissipationsenergie, q12 + j12. Daneben stellt sie die Differenz der spezifischen Enthalpie h2 − h1 dar. 89 Geschlossenes System In einem geschlossenen System kann eine isobare Zustandsänderung wie folgt verwirklicht werden, sieh Abb. 5.4: Ein Gas befindet sich in einem Zylinder und ist durch einen frei verschiebaren Kolben von der Umgebung getrennt. Der Druck im Zylinder steht zu jeder Zeit mit dem Umgebungsdruck im Gleichgewicht. Führt man dem Zylinder Wärme zu, so kann sich das Gas ungehindert ausdehen. Der Kolben verschiebt sich dabei so, dass der Druck im Zylinder stets mit dem Umgebungsdruck im Gleichgewicht bleibt. Abb. 5.4: Isobare Zustandsänderung in einem geschlossenen System Für die isobare Zustandsänderung im geschlossenen System gelten die folgenden Beziehungen: Thermische Zustandsgleichung: p = konst. (Gl. 5.13) Spezifische Volumenänderungsarbeit: 2 w V 12 = − ∫ p dv = − p ⋅ ( v 2 − v1 ) (Gl. 5.14) 1 1. HS für geschlossene Systeme: q12 + j12 = u2 − u1 + p ⋅ ( v 2 − v1 ) = h2 − h1 (Gl. 5.15) Durch Zufuhr von Wärme bzw. Dissipationsenergie wird die Enthalpie und damit die Temperatur erhöht. Die Gln. 5.13 bis 5.15 sind allgemeingültig, d. h., sie sind an kein spezielles Stoffmodell geknüpft. Möchte man allerdings die Differenz von spezifischer innerer Energie oder Enthalpie mit einer Temperaturdifferenz in Verbindung bringen, so muss man hierfür auf die kalorische Zustandsgleichung des betreffenden Mediums zurückgreifen, der spezielle Stoffmodelle zugrunde liegen. 90 Stationärer Fließprozess Stationäre Fließprozesse mit isobarer Zustandsänderung kommen in der Praxis näherungsweise in Rohrleitungen und Wärmeübertragern vor. Technische Arbeit geht dabei nicht über die Systemgrenze; es gilt wt12 = 0. Änderungen von kinetischer und potentieller Energie sind praktisch vernachlässigbar. Unter diesen Bedingungen ist auch die spezifische Dissipationsenergie j12 = 0, und der stationäre Fließprozess mit isobarer Zustandsänderung ist reversibel. Es gelten dann die folgenden Beziehungen: Thermische Zustandsgleichung: p = konst. (Gl. 5.16) Spezifische Druckänderungsarbeit: 2 w P12 = ∫ v dp = 0 (Gl. 5.17) 1 1. HS für stationäre Fließprozesse: q12 = h2 − h1 (Gl. 5.18) 91 5.4 Isotherme Zustandsänderung Bei einer isothermen Zustandsänderung bleibt unabhängig davon, ob der Prozess in einem geschlossenen oder offenen System stattfindet, die Temperatur konstant. Im T,s-Diagramm verläuft die Zustandsänderungslinie waagerecht. Den Verlauf einer isothermen Zustandsänderung im p,v-Diagramm kann man nur dann angeben, wenn die thermische Zustandsgleichung des Mediums bekannt ist. Für ideale Gase sind die Isothermen im p,v-Diagramm Hyperbeln. Abb. 5.5: Isotherme Zustandsänderung (1) → (2) eines idealen Gases im p,vund im T,s-Diagramm (vgl. Langeheinecke et al., 1999, S. 142) Abb. 5.5 zeigt die isotherme Zustandsänderung eines idealen Gases im p,v- und im T,s-Diagramm. Im p,v-Diagramm stellt die Fläche zwischen der Isothermen und der Abszisse die negative spezifische Volumenänderungsarbeit −wV12 und die Fläche zwischen der Isothermen und der Ordinate das Integral vdp bzw. die spezifische Druckänderungsarbeit wP12 dar. Im T,s-Diagramm ist die Fläche zwischen der Isothermen und der Abszisse die Summe aus übertragener spezifischer Wärme und zugeführter spezifischer Dissipationsenergie, q12 + j12. Zur Berechnung der Volumenänderungs- und der Druckänderungsarbeit benötigen wir den Verlauf der Zustandsänderungslinie im p,v-Diagramm. Aus diesem Grund reicht als Zustandsgleichung eine Angabe wie T = konst. nicht mehr aus. Zur Beschreibung des Verlaufs der Isothermen im p,v-Diagramm müssen wir deshalb auf ein geeignetes Stoffmodell zurückgreifen. Wir gehen im Folgenden von der thermischen Zustandsgleichung des idealen Gases aus: 92 Thermische Zustandsgleichung p⋅v = R⋅T führt mit konstanter Temperatur T zu p⋅ v = p1 ⋅ v1 , wobei die Variablen ohne Index für jeden Zustand auf der Zustandsänderungslinie stehen. Durch Umstellung erhält man p1 ⋅ v1 v p( v ) = und p1 ⋅ v1 p v( p) = (Gl. 5.19 a, b) sowie durch Einsetzen des Endzustandes (2): p1 ⋅ v1 = p2 ⋅ v 2 (Gl. 5.20) Geschlossenes System Eine isotherme Zustandsänderung in einem geschlossenen System kann man sich als Kompressionsprozess in einem sehr gut gekühlten Zylinder vorstellen. Setzt man Gl. 5.19 a in das Integral für die spezifische Volumenänderungsarbeit ein, 2 w V 12 = − ∫ p dv = 1 2 −∫ 1 p1 ⋅ v1 dv = − p1 ⋅ v1 v 2 ∫ 1 dv , v (Gl. 5.21) und löst das Integral, so erhält man mit Hilfe von Gl. 5.20 die folgenden Berechnungsgleichungen für die spezifische Volumenänderungsarbeit bei isothermer Zustandsänderung: w V 12 = p 2 ⋅ v 2 ln w V 12 v1 v2 v = R ⋅ T ln 1 v2 p2 p1 w V 12 = p 2 ⋅ v 2 ln w V 12 p = R ⋅ T ln 2 p1 (Gln. 5.22) Da die innere Energie des idealen Gases nur von der Temperatur abhängt, siehe Kap. 3.4, kann sich die innere Energie bei isothermer Zustandsänderung nicht ändern. Damit stellt sich der erste Hauptsatz für geschlossene Systeme bei isothermer Zustandsänderung wie folgt dar: q12 + w V 12 + j12 = u2 − u1 ⇒ = − q12 w V 12 + j12 = 0 (Gl. 5.23) 93 Bei einem Kompressionsprozess, der mit einem idealen Gas in einem geschlossenen System (Zylinder + Kolben) bei isothermer Zustandsänderung geführt wird, muss die zugeführte Arbeit, bestehend aus Volumenänderungsarbeit und Dissipationsenergie, in Form von Wärme wieder abgeführt werden, um die Temperatur des Gases konstant zu halten. Bei einem Expansionsprozess, der mit einem idealen Gas in einem geschlossenen System (Zylinder + Kolben) bei isothermer Zustandsänderung geführt wird, muss die abgeführte Arbeit, bestehend aus der um die Dissipationsenergie geminderten Volumenänderungsarbeit des Systems, in Form von Wärme zugeführt werden, um die Temperatur des Gases konstant zu halten. Stationärer Fließprozess Eine isotherme Zustandsänderung bei einem stationären Fließprozess kann man sich als Kompressionsprozess in einem sehr gut gekühlten Turbokompressor vorstellen. Zur Berechnung der spezifischen Druckänderungsarbeit setzen wir Gl. 5.19 b in das Integral vdp ein. In ähnlicher Weise wie bei der Volumenänderungsarbeit folgen als Lösung des Integrals einige Berechnungsgleichungen für die spezifische Druckänderungsarbeit. Man erhält: w P 12 = p 2 ⋅ v 2 ln w P 12 v1 v2 v = R ⋅ T ln 1 v2 p2 p1 w P 12 = p 2 ⋅ v 2 ln w P 12 p = R ⋅ T ln 2 p1 (Gln. 5.24) Vergleicht man die Gln. 5.24 mit den Gln. 5.22, so stellt man fest, dass für isotherme Zustandsänderungen wP12 = wV12 gilt. Da die Enthalpie wie die innere Energie des idealen Gases nur von der Temperatur abhängt, siehe Kap. 3.4, kann sich die Enthalpie bei isothermer Zustandsänderung nicht ändern. Damit stellt sich der erste Hauptsatz für stationäre Fließprozesse bei isothermer Zustandsänderung unter Vernachlässigung der äußeren Energien wie folgt dar: q12 + w t 12 = h2 − h1 = 0 ⇒ w t 12 = − q12 mit w t 12 = w P 12 + j12 w P 12 + j12 = − q12 (Gl.5.25) folgt (Gl. 5.26) 94 Damit gelten beim stationären Fließprozess ähnliche Aussagen wie beim geschlossenen System: Bei einem Kompressionsprozess, der mit einem idealen Gas in einem offenen System (Turbokompressor) bei isothermer Zustandsänderung geführt wird, muss die zugeführte technische Arbeit, bestehend aus Druckänderungsarbeit und Dissipationsenergie, in Form von Wärme wieder abgeführt werden, um die Temperatur des Gases konstant zu halten. Bei einem Expansionsprozess, der mit einem idealen Gas in einem offenen System (Turbine) bei isothermer Zustandsänderung geführt wird, muss die abgeführte technische Arbeit, bestehend aus der um die Dissipationsenergie verminderten Druckänderungsarbeit, in Form von Wärme zugeführt werden, um die Temperatur des Gases konstant zu halten. Isotherme Zustandsänderungen sind in der Praxis nur schwer zu verwirklichen. Sie bieten aber besondere Vorteile. Beispiel (vgl. Langeheinecke et al., 1999, S. 142): Eine Druckluftanlage soll stündlich 110 m³ Luft mit einem Absolutdruck von 16 bar und mit Umgebungstemperatur liefern. Der Verdichter saugt die Luft mit 0,96 bar und 20 °C an. Es soll von einem dissipationsfreien Prozess ausgegangen werden. Äußere Energien sollen vernachlässigt werden. a) Welcher Volumenstrom ist anzusaugen? b) Welche Leistung muss dem Verdichter zugeführt werden? c) Wie groß ist der zu übertragende Wärmestrom? • V 2 = 110 m 3 h = 0,0306 m 3 s Daten: Druckluftstrom Ansaugdruck p1 = 0,96 bar = 0,96 ⋅ 10 5 J m 3 Enddruck p 2 = 16 bar = 16 ⋅ 10 5 J m 3 Ansaugtemperatur t1 = 20 ° C; T1 = 293 K • a) Ansaugvolumenstrom V 1 • • v2 = v = V m • V1 p1 v1 p2 • p V2 16 bar ⋅ 0,0306 m 3 m3 = 2 = = 0,51 p1 0,96 bar s b) Zuzuführende Leistung P12 • P12 = m ⋅ wP 12 mit wP 12 = R ⋅ T ⋅ ln p2 v = p1 v1 ln 1 p1 v2 95 • • P12 = m ⋅ wP 12 = m ⋅ p1 v1 ⋅ ln P12 = 0,96 ⋅ 10 5 • p2 p = p1 ⋅ V 1 ⋅ ln 2 p1 p1 16 bar J m3 ⋅ 0 , 51 ⋅ ln = 138 kW 3 s 0,96 bar m • c) Übertragener Wärmestrom Q 12 • Q 12 = − P12 = − 138 5.5 kJ s Isentrope Zustandsänderung Wir verstehen unter einer isentropen Zustandsänderung eine reversible Zustandsänderung in einem adiabaten System. Unabhängig davon, ob sich der Vorgang in einem geschlossenen oder offenen System abspielt, bleibt bei einer isentropen Zustandsänderung die Entropie konstant, siehe Kap. 4.5. Im T,s-Diagramm verläuft die Zustandsänderungslinie deshalb senkrecht. Bei einer isentropen Zustandsänderung ändern sich Druck, Temperatur und spezifisches Volumen gleichzeitig. Unter der Bedingung dq = 0 (adiabat) und dj = 0 (reversibel) lässt sich aus dem ersten Hauptsatz eine Differentialgleichung entwickeln, die den Verlauf der isentropen Zustandsänderung im p,v-Diagramm beschreibt: κ v dp = ≡ − p dv s = konst . dh du (Gl. 5.27) Die durch Gl. 5.27 definierte Größe κ wird als Isentropenexponent bezeichnet. Isentropengleichungen für ideale Gase Die Integration der Differentialgleichung 5.27 führt auf die folgenden Beziehungen zwischen dem Druck p und dem spezifischen Volumen v bei einer isentropen Zustandsänderung: 1 κ p κ v1 = 2 v2 p1 v p2 = 1 ; p1 v2 (Gl. 5.28 a, b) bzw. κ p1 ⋅ v1 = p ⋅ vκ = p2 ⋅ v 2 κ (Gl.5.29) In Gl. 5.29 stehen die Variablen ohne Index für alle Zustände auf der Zustandsänderungslinie. 96 Ein Zusammenhang mit der Temperatur kann hergestellt werden, wenn der Verlauf der Isothermen im p,v-Diagramm bekannt ist, d. h. ein Stoffmodell zugrunde liegt. Wir verwenden die thermische Zustandsgleichung des idealen Gases und formulieren sie für den Anfangs- und den Endzustand: p1 ⋅ v1 = R T1 und p2 ⋅ v 2 = R T2 (Gl. 5.30 a, b) Wir verknüpfen beide Gleichungen über die Gaskonstante und erhalten: p2 T v = 2⋅ 1 p1 T1 v 2 bzw. v1 T p = 1⋅ 2 v2 T2 p1 (Gl. 5.31 a, b) Setzt man nun zunächst Gl. 5.31 a und dann Gl. 5.31 b in Gl. 5.28 ein, so erhält man Beziehungen zwischen der Temperatur T und dem Druck p sowie zwischen der Temperatur T und dem spezifischen Volumen v bei einer isentropen Zustandsänderung: v T2 = 1 T1 v2 1 κ −1 p T2 = 2 T1 p1 ; κ −1 κ T κ −1 v1 = 2 v2 T1 (Gl. 5.32 a, b) κ ; T κ −1 p2 = 2 p1 T1 (Gl. 5.33 a, b) Die Gln. 5.28, 5.32 und 5.33 werden als Isentropengleichungen bezeichnet. Abb. 5.6: Isentrope Zustandsänderung (1) → (2) eines idealen Gases im p,vund im T,s-Diagramm (vgl. Langeheinecke et al., 1999, S. 146) Abb. 5.6 zeigt die isentrope Zustandsänderung eines idealen Gases im p,v- und im T,s-Diagramm. Im p,v-Diagramm ist die Isentrope eine Parabel. Für einen gegebenen Zustandspunkt, z. B. Punkt (1) im p,v-Diagramm der Abb. 5.6, verläuft sie steiler als die entsprechende Isotherme. Die Fläche zwischen der Isentropen und der 97 v-Achse stellt die negative spezifische Volumenänderungsarbeit −wV12 und die Fläche zwischen der Isentropen und der p-Achse das Integral vdp bzw. die spezifische Druckänderungsarbeit wP12 dar. Im T,s-Diagramm existiert wegen q12 + j12 = 0 keine Fläche zwischen der Zustandsänderungslinie und der Abszisse. Für ideale Gase ist laut Gl. 3.54 und 3.55 du = cV⋅dT und dh = cP⋅dT. Setzt man dies in Gl. 5.27 ein, so folgt daraus der Isentropenexponent für ideale Gase: κ dh du = = cP cV (Gl.5.34) Er ist identisch mit dem Verhältnis von isobarer und isochorer Wärmekapazität und damit eine Stoffgröße. Da stets cP > cV gilt, ist κ > 1. Geschlossenes System Eine isentrope Zustandsänderung in einem geschlossenen System kann man sich als verlustfreien Kompressionsprozess in einem sehr gut isolierten, d. h. adiabaten Zylinder vorstellen. Zur Berechnung der Volumenänderungsarbeit geht man ähnlich vor, wie bei der isothermen Zustandsänderung: Gl. 5.29 wird nach p(v) umgestellt und in das Integral der spezifischen Volumenänderungsarbeit eingesetzt. Schließlich erhält man, auch unter Zuhilfenahme der thermischen Zustandsgleichung des idealen Gases und der Isentropengleichungen 5.28, 5.32 und 5.33 diverse Berechnungsgleichungen für die spezifische Volumenänderungsarbeit bei isentroper Zustandsänderung eines idealen Gases mit konstanter spezifischer Wärmekapazität: wV 12 κ −1 R ⋅ T1 p 2 κ − 1 = ⋅ κ − 1 p1 (Gl. 5.35) wV 12 κ −1 R ⋅ T1 v1 − 1 = ⋅ κ − 1 v 2 (Gl. 5.36) wV 12 = R ⋅ (T − T1 ) = c V ⋅ (T2 − T1 ) κ −1 2 (Gl. 5.37) Welche dieser Gleichungen zur Berechnung herangezogen wird, hängt davon ab, welche Größen in der Aufgabenstellung gegeben sind. Der erste Hauptsatz für geschlossene Systeme reduziert sich wegen q12 = 0 und j12 = 0 für die isentrope Zustandsänderung auf die Beziehung: wV 12 = u2 − u1 (Gl. 5.38) 98 Stationärer Fließprozess Ein Beispiel für eine isentrope Zustandsänderung bei einem stationären Fließprozess ist ein verlustfreier Kompressionsprozess, der in einem sehr gut isolierten, d. h. adiabaten Turbokompressor stattfindet. Für die spezifische Druckänderungsarbeit bei einer isentropen Zustandsänderung eines idealen Gases mit konstanter spezifischer Wärmekapazität lassen sich die folgenden Berechnungsgleichungen finden: wP 12 κ −1 κ p κ 2 − 1 = ⋅ R ⋅ T1 ⋅ κ −1 p 1 (Gl. 5.39) w P 12 v κ − 1 − 1 = ⋅ R ⋅ T1 ⋅ 1 κ −1 v 2 (Gl. 5.40) wP 12 = κ κ ⋅ R ⋅ (T2 − T1 ) = cP ⋅(T2 − T1 ) κ −1 (Gl. 5.41) Vergleicht man die Gln. 5.39 bis 5.41 mit den Gln. 5.35 bis 5.37, so stellt man fest, dass für isentrope Zustandsänderungen wP12 = κ ⋅ wV12 gilt. Der erste Hauptsatz für stationäre Fließprozesse und die Gleichung für die spezifische technische Arbeit reduzieren sich und unter Vernachlässigung von äußeren Energien bei isentroper Zustandsänderung auf: wt 12 = h2 − h1 (Gl. 5.42) und wt 12 = wP 12 (Gl. 5.43) 99 5.6 Polytrope Zustandsänderung Wenn man die bisher behandelten speziellen Zustandsänderungen des idealen Gases zusammen in ein p,v-Diagramm und ein T,s-Diagramm einträgt, siehe Abb. 5.7, so zeigt sich, dass sich diese Zustandsänderungslinien als zu einem Kurvenbüschel gehörend ansehen lassen. Abb. 5.7: Spezielle Zustandsänderungen idealer Gase im p,v- und im T,sDiagramm (Langeheinecke et al., 1999, S. 148) Die speziellen Zustandsänderungen können als Spezialfälle eines allgemeinen Gesetzes aufgefasst werden: p ⋅ vn = konst . mit −∞ ≤ n ≤ +∞ (Gl. 5.44) Gl. 5.44 wird als Polytropengleichung und die durch sie beschriebenen Kurven als Polytropen bezeichnet. Der in Gl. 5.44 enthaltene Exponent n heißt Polytropenexponent. Es bedeuten: n n n n = = = = 0 1 κ ∞ p T s v = = = = konst. konst. konst. konst. isobare Zustandsänderung isotherme Zustandsänderung isentrope Zustandsänderung isochore Zustandsänderung Eine polytrope Zustandsänderung mit beliebigem Polytropenexponenten n kann praktisch zu jedem denkbaren Ort, d. h. Zustand im p,v-Diagramm und im T,sDiagramm führen. Der technisch wichtige Bereich polytroper Zustandsänderungen liegt jedoch zwischen 1 ≤ n ≤ κ, d. h. zwischen der isothermen und der isentropen Zustandsänderung. Es bedeutet n = 1 eine ideal gute Wärmeübertragung und n = κ eine ideal gute Isolierung. Beides ist in technischen Anlagen nur näherungsweise zu verwirklichen, weil weder eine exakte Temperaturkonstanz noch eine völlige Wärmeisolierung möglich sind. 100 Formal ist die Polytropengleichung, Gl. 5.44 — wenn man n mit κ identifiziert — wie die Isentropengleichung, Gl. 5.29, aufgebaut. Die Bedeutung der beiden Exponenten ist dabei aber völlig verschieden: Die Größe κ ist durch die thermodynamischen Eigenschaften des Fluids, beim idealen Gas durch die Wärmekapazitäten cP und cV, als Zahlenwert festgelegt. Durch den Polytropenexponenten n versucht man eine aufgrund eines technischen Prozesses vorliegende Zustandsänderung auf einfache Weise mathematisch zu approximieren und damit berechenbar zu machen. Polytrope Zustandsänderungen unterliegen zunächst keinen Beschränkungen. Für sie gilt im Allgemeinen, dass q12 und j12 nicht null sind. Im Speziellen können Zustandsänderungen jedoch auch durch adiabate Polytropen oder dissipationsfreie Polytropen beschrieben werden. Polytropengleichungen für ideale Gase Analog zu den Gleichungen der isentropen Zustandsänderung lassen sich mit Hilfe der thermischen Zustandsgleichung des idealen Gases verschiedene Darstellungen der Polytropengleichung angeben: n p v1 = 2 v2 p1 v p2 = 1 ; p1 v2 v T2 = 1 T1 v2 p T2 = 2 T1 p1 1 n (Gl. 5.45 a, b) 1 n −1 ; n −1 n T n −1 v1 = 2 v2 T1 (Gl. 5.46 a, b) n ; T n −1 p2 = 2 p1 T1 (Gl. 5.47 a, b) Manchmal muss der Polytropenexponent aus gegebenen Zustandsgrößen bestimmt werden. Das ist z. B. der Fall, wenn ein neuer Verdichter entwickelt und gebaut wurde. Für diese Maschine kennt der Hersteller den Polytropenexponenten zunächst nicht. Auf dem Prüfstand werden deshalb z. B. Eintrittsdruck und -temperatur sowie Austrittsdruck und -temperatur gemessen. Aufgrund dieser Daten lässt sich der Polytropenexponent mit Hilfe von Gl. 5.47 berechnen. Stellt man diese Gleichung nach n um, so folgt: ln n = p1 p2 p T ln 1 − ln 1 p2 T2 (Gl. 5.48) 101 Geschlossene Systeme Für die bei Prozessen in geschlossenen Systemen wichtige spezifische Volumenänderungsarbeit erhält man bei polytroper Zustandsänderung idealer Gase: wV 12 n −1 R ⋅ T1 p 2 n − 1 = ⋅ n − 1 p1 (Gl. 5.49) wV 12 n −1 R ⋅ T1 v1 − 1 = ⋅ n − 1 v 2 (Gl. 5.50) wV 12 = R ⋅ (T2 − T1 ) n −1 (Gl. 5.51) Für die polytrope Zustandsänderung gilt der erste Hauptsatz für geschlossene Systeme in seiner allgemeinen Form: q12 + w12 = u2 − u1 mit = wV 12 + j12 w12 (Gl. 5.52) Stationäre Fließprozesse Für die bei stationären Fließprozessen wichtige spezifische Druckänderungsarbeit erhält man bei polytroper Zustandsänderung idealer Gase:: w P 12 n −1 n p n 2 − 1 = ⋅ R ⋅ T1 ⋅ p1 n −1 (Gl. 5.53) w P 12 v n − 1 n − 1 = ⋅ R ⋅ T1 ⋅ 1 n −1 v 2 (Gl. 5.54) wP 12 = n ⋅ R ⋅ (T2 − T1 ) n −1 (Gl. 5.55) Vergleicht man die Gln. 5.53 bis 5.55 mit den Gln. 5.49 bis 5.51, so stellt man fest, dass für polytrope Zustandsänderungen wP12 = n ⋅ wV12 gilt. Für die polytrope Zustandsänderung gilt der erste Hauptsatz für stationäre Fließprozesse in seiner allgemeinen Form: 102 ( ) ( ) 1 2 2 ⋅ c 2 − c1 + g ⋅ z 2 − z1 2 1 2 2 = j12 + w P 12 + ⋅ c 2 − c1 + g ⋅ z 2 − z1 2 q12 + w t 12 = h2 − h1 + ( mit w t 12 5.7 Kreisprozesse ) ( ) (Gl. 5.56) Die bisher behandelten Zustandsänderungen wurden mit dem Fluid jeweils einmal durchgeführt, wobei sich sein Zustand von (1) nach (2) änderte. Aus einer bestimmten Arbeitsmittelmenge kann dabei nur einmalig ein gewisser Betrag an Arbeit gewonnen werden. Das gilt sowohl für offene, als auch für geschlossene Systeme. Viele Maschinen arbeiten periodisch, d. h. ein bestimmter Prozess wird immer wieder durchlaufen, wobei z. B. laufend Arbeit abgegeben werden kann. Um eine derartige Wiederholung zu erreichen, ist es erforderlich, den Ausgangszustand des Arbeitsmediums wiederherzustellen, d. h. den Anfangsdruck, die Anfangstemperatur usw.. Eine solche Folge von Prozessen, durch die schließlich der Anfangszustand wieder erreicht wird, nennt man Kreisprozess. Im p,v-Diagramm und im T,s-Diagramm ist er durch einen geschlossenen Linienzug darstellbar, Abb. 5.8. Abb. 5.8: Kreisprozess im p,v-Diagramm und im T,s-Diagramm Wir definieren: Ein Kreisprozess ist eine Folge von Zustandsänderungen, durch die der Ausgangszustand wieder hergestellt wird. Ein Prozess, der eine von (1) nach (2) abgelaufene Zustandsänderung auf demselben Weg von (2) nach (1) wieder rückgängig macht, wird dabei mindestens dieselbe Arbeit zugeführt werden müssen, wie zuvor auf dem Weg von (1) nach (2) abgeführt wurde. Bei der technischen Realisierung eines Kreisprozesses läuft häufig ein Arbeitsmittel als stationär strömendes Fluid um. Ein Beispiel dafür ist die in Abb. 5.9 skizzierte Dampfkraftanlage, bei der Wasserdampf als Arbeitsmittel im Dampferzeuger konti103 nuierlich Wärme aufnimmt und in der Turbine bei starker Enthalpieabnahme mechanische Arbeit abgibt. Im Kondensator wird dem Fluid Wärme entzogen, und die Speisepumpe pumpt das Kondensat wieder in den Dampferzeuger. Abb. 5.9: Dampfkraftanlage als Beispiel eines Kreisprozesses Bei diesem Prozess durchströmt das stationär umlaufende Fluid die hintereinander geschalteten offenen Systeme Dampferzeuger, Turbine, Kondensator und Speisepumpe. Wir betrachten einen Teilprozess des gesamten Kreisprozesses, z. B. die Turbine aus Abb. 5.9. Die Zustände am Ein- und Austritt sollen durch die Indizes i und i + 1 gekennzeichnet sein. Für das stationär umlaufende Fluid lässt sich für diesen Teilbereich der erste Hauptsatz in gewohnter Weise, z. B. in spezifischen Größen angeben: q i , i +1 + w t i , i +1 = h i + 1 − h i + ( ) ( 1 2 2 ⋅ c i +1 − c i + g ⋅ z i +1 − z i 2 ) (Gl. 5.57) Die Endgrößen des einen Teilprozesses sind die Anfangsgrößen des nächsten Teilprozesses. Summiert man über alle Teilprozesse und beachtet, dass der Endzustand des Fluids nach dem Durchlauf mit dem Ausgangszustand übereinstimmen muss, so verschwindet die rechte Seite von Gl. 5.57 und wir erhalten: ∑q i , i +1 + ∑w t i , i +1 = 0 (Gl. 5.58) Handelt es sich um differentiell kleine Zustandsänderungen, aus denen der Gesamtprozess zusammengesetzt ist, so tritt an die Stelle der Summation eine Integration (Kreisintegral) 104 ∫ dq + ∫ dw t = 0 (Gl. 5.59) Definition der spezifischen Kreisprozessarbeit: Als spezifische Kreisprozessarbeit wKP wollen wir die Summe der technischen Arbeiten der Teilprozesse bzw. das Kreisintegral über dwt definieren: w KP ≡ ∑w t i , i +1 = ∫ dw t (Gl. 5.60) Erster Hauptsatz für Kreisprozesse: Den ersten Hauptsatz für Kreisprozesse erhalten wir dann in der Schreibweise − w KP = ∑q i , i +1 = ∫ dq (Gl. 5.61) Die negative Kreisprozessarbeit ist gleich der algebraischen Summe aller vom Arbeitsfluid aufgenommenen und abgegebenen spezifischen Wärmen. Die gesamte bei einem Kreisprozess ausgetauschte spezifische Wärme lässt sich in einen Anteil qzu, der alle zugeführten Teilwärmen enthält, und einen Anteil qab, der alle vom Fluid abgegebenen Teilwärmen enthält, aufspalten: ∑q i , i +1 = q zu + q ab (Gl. 5.62) Die Energiebilanz für den Kreisprozess nimmt dann die Form an: − w KP = q zu + q ab 1. HS für Kreisprozesse (Gl. 5.63) Die spezifische Kreisprozessarbeit −wKP ist gleich der Summe aus der dem Arbeitsmittel zugeführten und der von ihm abgegebenen spezifischen Wärmen. Es ist zu beachten, dass sich hinter den abgegebenen spezifischen Wärmen negative Zahlenwerte verbergen. Wenn die Summe aus zu- und abgeführter Wärme qzu + qab > 0 ist, dann gibt der Kreisprozess Arbeit ab. Dies ist in Wärmekraftanlagen der Fall, wo kontinuierlich Wärme in Arbeit umgewandelt wird. Abb. 5.9 zeigt solch eine Anlage. Die Energieumwandlung in einer Wärmekraftanlage lässt sich in einem Energieflussdiagramm — einem sog. SANKEY-Diagramm — veranschaulichen, siehe Abb. 5.10. 105 Abb. 5.10: SANKEY-Diagramm des Kreisprozesses einer Wärmekraftanlage Die Güte der Energieumwandlung wird durch den thermischen Wirkungsgrad angeben. η th = abgeführte Kreisprozessarbeit energetischer Nutzen = zugeführte Wä rme energetischem Aufwand η th = w KP q zu = q zu − q ab q zu = 1 − q ab q zu (Gl. 5.64) Die Größe ηth ist ein Umwandlungsfaktor für Wärme in Arbeit. Er ist immer wesentlich kleiner als eins. Wenn die Summe aus zu- und abgeführter Wärme qzu + qab < 0 ist, dann nimmt der Kreisprozess Arbeit auf. Derartige Verhältnisse liegen in Kälteanlagen und Wärmepumpen vor. Aus Abb. 5.11 ist der prinzipiell ähnliche Aufbau wie bei einer Dampfkraftanlage erkennbar. 106 Abb. 5.11: Kälteanlage / Wärmepumpe als Beispiel eines Kreisprozesses Hier muss insgesamt Arbeit aufgewendet werden, um Wärme entgegen dem natürlichen Temperaturgefälle auf ein höheres Temperaturniveau zu transportieren. Die Güte des Transportes wird durch die Leistungsziffer ε angegeben. Obwohl Kälteanlagen und Wärmepumpen technisch identisch sind, ist die Leistungsziffer bei Kälteanlagen etwas anders definiert als bei Wärmepumpen: εK = q zu q zu = > 0 w KP q ab − q zu εW = q ab w KP = q ab q ab − q zu > 1 (Gl. 5.65) (Gl. 5.66) Der Unterschied der Leistungsziffern von Kälteanlage und Wärmepumpe ist in dem unterschiedlichen energetischen Nutzen begründet: Bei einer Kälteanlage arbeitet der Kreisprozess zwischen dem zu kühlenden Raum und der Umgebung, Abb. 5.12 a. Aus dem zu kühlenden Raum wird Wärme auf das Temperaturniveau der Umgebung gefördert. Der energetische Nutzen ist hierbei die Wärme, die dem Kreisprozess aus dem zu kühlenden Raum zugeführt wird. Bei einer Wärmepumpe arbeitet der Kreisprozess zwischen der Umgebung und einem zu beheizenden Raum, Abb. 5.12 b. Aus der Umgebung wird Wärme auf das höhere Temperaturniveau des zu beheizenden Raumes gefördert. Der energetische Nutzen ist in diesem Fall die vom Kreisprozess an den Raum abgegebene Wärme. 107 Abb. 5.12: SANKEY-Diagramme der Kreisprozesse einer Kälteanlage und einer Wärmepumpe Bei der bisherigen Behandlung wurde der Kreisprozess als aus einer Folge von stationären Fließprozessen bestehend angenommen. Man kann sich leicht vorstellen, dass die gleichen Überlegungen auch für ein geschlossenes System gelten, über dessen Grenzen in einem Zyklus nacheinander Energie in Form von Wärme und Arbeit wechseln, so wie es beispielsweise bei Kolbenmotoren der Fall ist. Rechtsläufige und linksläufige Kreisprozesse: Hinsichtlich des Umlaufsinns im p,v- und T,s-Diagramm unterscheidet man zwischen rechtsläufigen und linksläufigen Kreisprozessen. Bei einem rechtsläufigen Kreisprozess ist die spezifische Kreisprozessarbeit wKP < 0, d. h. das System gibt Arbeit ab. Bei einem linksläufigen Kreisprozess ist wKP > 0, d. h. das System nimmt Arbeit auf. In Wärmekraftanlagen laufen Rechtsprozesse ab. In Kälteanlagen und Wärmepumpen durchläuft das Arbeitsmedium einen Linksprozess. Dissipationsfreier Kreisprozess: Bei verlustfreien Kreisprozessen lässt sich die technische Arbeit jedes differentiellen Teilschritts unter Vernachlässigung äußerer Energien als 108 dw t = dw P = v ⋅ dp (Gl. 5.67) darstellen. Für die Kreisprozessarbeit folgt damit nach der Definition von Gl. 5.60: w KP = ∫ dw t = ∫ v dp (Gl. 5.67) Das bedeutet: Bei einem verlustfreien Kreisprozess eines stationär umlaufenden Fluids ist im p,v-Diagramm die von der Zustandsänderungslinie eingeschlossene Fläche mit dem Betrag der spezifischen Kreisprozessarbeit identisch. In ähnlicher Weise lässt sich mit Hilfe der Beziehungen des zweiten Hauptsatzes zeigen: Bei einem verlustfreien Kreisprozess ist im T,s-Diagramm die von der Zustandsänderungslinie eingeschlossene Fläche mit dem Betrag der spezifischen Kreisprozessarbeit identisch. Abb. 5.13: Darstellung der spezifischen Kreisprozessarbeit im p,v- und T,s-Diagramm Die bislang getroffenen Aussagen gelten für alle Kreisprozesse gleichermaßen. Möchte man nun z. B. wissen, wie groß der thermische Wirkungsgrad eines rechtsdrehenden Kreisprozesses ist, so hängt die Beantwortung dieser Frage von der konkreten Realisierung des Kreisprozesses ab. Es gibt einige technische Lösungen für Rechtsprozesse, die alle dasselbe Ziel haben, Wärme in Arbeit umzuwandeln, dies aber mit unterschiedlicher Effizienz tun. So ist bei gleicher abgeführter Kreisprozessarbeit der thermische Wirkungsgrad eines Dieselprozesses höher als 109 der eines Ottoprozesses, was sich beim Dieselmotor durch einen niedrigeren Treibstoffverbrauch bemerkbar macht. Im Folgenden sei der CARNOT-Prozess als Beispiel für einen rechtslaufenden Kreisprozess vorgestellt. Dieser historisch älteste Kreisprozess wurde 1824 von dem Franzosen CARNOT vorgeschlagen. Als Rechtsprozess ist er ein Arbeitsprozess für Wärmekraftanlagen, der aus den folgenden dissipationsfreien Teilprozessen besteht: Abb. 5.14: (1) (2) (3) (4) → → → → (2) (3) (4) (1) Darstellung des CARNOT-Prozesses im p,v- und T,sDiagramm sowie Verfahrensschema zu seiner Durchführung isentrope Kompression isotherme Expansion mit Wärmezufuhr isentrope Expansion isotherme Kompression mit Wärmeabfuhr Abb. 5.14 zeigt die Darstellung des Prozesses im p,v- und im T,s-Diagramm und das Schaltschema der Wärmekraftanlage. Bei der Expansion in der Turbine wird dem System Wärme bei konstanter Temperatur zugeführt. Bei der isothermen Kompression im Verdichter wird Wärme bei konstanter Temperatur abgeführt. Für die einzel110 nen Teilprozesse des stationär und verlustfrei umlaufenden Fluids können unter der Voraussetzung eines idealen Gases mit konstanter spezifischer Wärmekapazität (z. B. Helium) die spezifische technische Arbeit und die übertragene spezifische Wärme angegeben werden (äußere Energien sind vernachlässigt): (1) → (2): isentrope Kompression w t 12 = κ κ −1 q12 = 0 R (T2 − T1 ) (2) → (3): isotherme Expansion T2 = T3 w t 23 = − q 23 = R ⋅ T2 ⋅ ln (3) → (4): isentrope Expansion w t 34 = κ κ −1 q34 = 0 R (T4 − T3 ) = (4) → (1): isotherme Kompression w t 41 = − q 41 = R ⋅ T4 ⋅ ln Es gilt p3 p2 κ κ −1 R (T1 − T2 ) = − w t 12 T4 = T1 p1 p = R ⋅ T4 ⋅ ln 2 p4 p3 p1 p = 2 , weil für ideale Gase die Isobaren im p4 p3 T,s-Diagramm horizontal parallel verlaufen. Die spezifische Kreisprozessarbeit des CARNOT-Prozesses lässt sich sowohl aus der Summe der spezifischen technischen Arbeiten als auch aus der negativen Summe der spezifischen Teilwärmen q berechnen: wKP = w t 12 + w t 23 + w t 34 + w t 41 = R ⋅ (T2 − T4 ) ln p3 p2 = R ⋅ (T2 − T4 ) ln p3 p2 wKP = − q 23 − q 41 Der thermische Wirkungsgrad des rechtslaufenden CARNOT-Prozesses lautet damit: η th,C = wKP q zu η th,C = 1 − = T4 T2 − R (T2 − T4 ) ln p3 p 2 − R T2 ln p3 p 2 bzw. (Gl. 5.68) Der thermische Wirkungsgrad des CARNOT-Prozesses ist unabhängig von den Eigenschaften des Arbeitsmittels. Er hängt nur von den Temperaturen T2 (Temperatur 111 der Wärmezufuhr) und T4 (Temperatur der Wärmeabfuhr) ab, zwischen denen er verläuft. Für eine Temperatur der Wärmeabfuhr von T4 = 0 K wird er gleich eins, d. h. die gesamte zugeführte Wärme würde in Arbeit verwandelt werden. Im Allgemeinen ist die Temperatur T4 jedoch mit der Umgebungstemperatur identisch, so dass schon deswegen der thermische Wirkungsgrad deutlich kleiner als eins wird. Um einen guten Wirkungsgrad zu erzielen, muss die Wärme dem Prozess bei möglichst hoher Temperatur T2 zugeführt werden. Der CARNOT-Prozess ist der Kreisprozess, der den höchstmöglichen thermischen Wirkungsgrad liefert. Seiner technischen Realisierung stehen allerdings verschiedene verfahrenstechnische Hindernisse im Wege. Er hat damit lediglich akademischen Wert. Der auch als CARNOT-Faktor bezeichnete thermische Wirkungsgrad des CARNOT-Prozesses wird als Maßstab für die Wirkungsgrade von technisch realisierbaren Kreisprozessen verwendet. Er stellt die Wirkungsgradgrenze dar, die von einem wirklichen Prozess aufgrund der Beschränkungen, die durch den zweiten Hauptsatz der Thermodynamik vorgegeben sind, bestenfalls erreicht werden kann. Geht man z. B. von der höchsten und niedrigsten Temperatur im Kreisprozess eines Dampfkraftwerkes aus, tmax = 600 °C (873 K) und tmin = 30 °C (303 K), so hätte ein zwischen diesen Temperaturen geführter CARNOT-Prozess einen thermischen Wirkungsgrad von η th, C = 1 − 303 K = 0, 653 , 873 K d. h., maximal 65,3 % der zugeführten Brennstoffenergie, die in der Feuerung eines realen Kraftwerkes freigesetzt und an den Wasser-/Dampf-Kreisprozess übertragen wird, kann in Kreisprozessarbeit und damit in elektrischen Strom umgewandelt werden. Der tatsächliche thermische Wirkungsgrad eines Dampfkraftwerkes, das zwischen den angegeben Grenztemperaturen arbeitet, liegt mit etwa 48 % deutlich niedriger. Es ist für rechtsläufige Kreisprozesse charakteristisch, dass für ihre Durchführung nicht nur eine Wärmequelle mit möglichst hohem Temperaturniveau vorhanden sein muss, sondern ebenso eine Wärmesenke mit möglichst niedriger Temperatur, um Kreisprozessarbeit zu gewinnen. Die Wärmesenke, d. h. die Wärmeabfuhr an die Umgebung (Abwärme), ist für den Prozess zwingend erforderlich, da das Kreisprozessfluid ohne sie seinen Ausgangszustand nicht wieder erreichen kann. Es kann somit nicht gelingen die einem Kreisprozess zugeführte Wärme vollständig in Kreisprozessarbeit umzuwandeln. Im Gegensatz dazu ist es durchaus möglich, mechanische Energie über einen Reibungsvorgang vollständig in Wärme umzuwandeln. Es scheint offenbar ein grundsätzlicher Unterschied zwischen der Wandlung von Arbeit in Wärme und deren Umkehrung, der Wandlung von Wärme in Arbeit, zu bestehen. Kontrollfragen 112 5.1 Eine Gasflasche mit offenem Ventil erwärmt sich in der Sonne. Welche Systemeigenschaft und welche Zustandsänderung ist für dieses System zutreffend? 5.2 Bei welcher reversiblen Zustandsänderung ist die spezifische technische Arbeit gleich der spezifischen Volumenänderungsarbeit? 5.3 Ein ideales Gas soll in einem stationären Fließprozess verlustfrei verdichtet werden. Ist es hinsichtlich der aufzuwendenden technischen Arbeit günstiger, den Verdichtungsprozess isotherm oder isentrop zu führen? Benutzen Sie für Ihre Überlegungen ein p,v-Diagramm. 5.4 Eine Turbine gibt über ihre Welle technische Arbeit und über ihr Gehäuse Wärme ab. Bei der Expansion des Arbeitsmittels sinken Druck und Temperatur. Durch welche Zustandsänderung kann dieser Prozess beschrieben werden? Wie heißt die maßgebliche Größe? 5.5 Was versteht man unter einem Kreisprozess? Welche grundlegenden thermodynamischen Aufgaben können mit Hilfe von Kreisprozessen bewältigt werden? 5.6 Welchen Stellenwert hat der CARNOT-Prozess als Wärmekraftprozess für die Praxis und für die vergleichende Betrachtung? 113 Übungsaufgaben 5.1 In einem geschlossenen System sollen m = 5 kg Luft ausgehend von t1 = 20 °C, p1 = 1 bar auf p2 = 6 bar verdichtet werden, und zwar: a) isotherm b) isentrop c) polytrop mit n = 1,2 In allen Fällen soll die Zustandsänderung dissipationsfrei erfolgen. Die Luft soll sich wie ein ideales Gas mit R = 287 J/(kg K) und cP = 1006 J/(kg K) verhalten. Gesucht sind: wV12, T2, q12. 5.2 Ein Turboverdichter verdichtet Luft [ideales Gas, R = 287 J/(kg K), cP = 1004 J/(kg K) = konst.] von einem Zustand p1 = 2 bar, T1 = 293 K auf einen Druck von p2 = 5 bar. Die Zustandsänderung sei polytrop, der Polytropenexponent ist n = 1,2. Der Massenstrom der Luft beträgt 0,1 kg/s, die Durchmesser von Ansaugleitung und Druckleitung sind d1 = 100 mm bzw. d2 = 70 mm. Ein- und Austrittsstutzen befinden sich auf gleicher Höhe. a) Es sind die thermischen Zustandsgrößen sowie die Ein- und Austrittsgeschwindigkeiten zu berechnen. b) Wie groß ist die zuzuführende spezifische technische Arbeit wt12, wenn 5 % davon dissipiert werden? c) Wie groß ist die ausgetauschte spezifische Wärme q12? 114 • 5.3 Ein Luftstrom von V 1 = 10 m³/h wird von einer Kaltluftanlage zur Raumkühlung aus einem zu kühlenden Raum angesaugt. Der Zustand der Luft in dem Raum ist p1 = 1 bar, T1 = 278 K. Die Luft wird in aufeinander folgenden stationären Fließprozessen den nachstehenden Zustandsänderungen unterworfen (linkslaufender JOULEProzess): (1) (2) (3) (4) Isentrope Verdichtung im Turbokompressor auf p2 = 2 bar. Isobare Abkühlung in einem Wärmeübertrager auf T3 = 310 K. Isentrope Expansion in einer Turbine auf p4 = 1 bar. Isobare Wärmezufuhr im zu kühlenden Raum auf T1 = 278 K. Die Luft kann in dem betrachteten Zustandsbereich als ideales Gas mit konstanten spezifischen Wärmekapazitäten behandelt werden. R = 287 J / (kg K) cP = 1004 J / (kg K) κ = 1,4 Luftfeuchtigkeit, Dissipation und äußere Energien sind in allen Teilprozessen zu vernachlässigen. a) Zeichnen Sie das Verfahrensschema der Kaltluftanlage b) Stellen Sie den Kreisprozess im p,v- und im T,s-Diagramm dar. c) Wie groß ist die höchste und niedrigste Temperatur? d) Wie groß sind die zu- und abgeführten Wärmeströme? e) Welche Leistung benötigt der Verdichter? f) Welche Leistung gibt die Turbine ab? g) Berechnen Sie die Kreisprozessleistung PKP. h) Welche Leistungsziffer εK hat die Kälteanlage? 115 6. Thermische und kalorische Stoffeigenschaften realer Stoffe Die allgemeinen Beziehungen der Thermodynamik wie der erste und der zweite Hauptsatz können in der Praxis nur angewandt werden, wenn die physikalischen Eigenschaften der Stoffe, die in die Rechnungen eingehen, bekannt sind. Diese Eigenschaften der Stoffe sind in der thermischen und kalorischen Zustandsgleichung zusammengefasst. Während die thermische Zustandgleichung eines Stoffes durch Messung der Zustandsgrößen p, T und v bestimmt werden müssen, können die kalorischen Zustandgrößen auf der Basis der Beziehungen des 2. Hauptsatzes aus einer bekannten thermischen Zustandsgleichung berechnet werden (vgl. Baehr, 1973, S.157). 6.1 Das p,v,T-Diagramm für reine reale Stoffe Wie wir bereits in Abschn. 2.3 gesehen haben, gibt es für die Gleichgewichtszustände eines jeden Stoffes eine thermische Zustandsgleichung der Form F(p,v,T) = 0. Sie lässt sich geometrisch als Fläche im dreidimensionalen p,v,T-Raum darstellen, indem man über der v,T-Ebene den Druck p = p(v,T) als Ordinate aufträgt. Für den einfachen Modellfall des idealen Gases führt dies zu einer einfachen Zustandsfläche mit hyperbolischer Gestalt, siehe Abb. 2.9. Da im Gegensatz zum idealen Gas alle realen Stoffe in den Aggregatzuständen oder Phasen fest, flüssig und gasförmig vorkommen, nimmt die Zustandsfläche für diese Stoffe eine weitaus komplexere Gestalt an. Wie in Abb. 6.1 zu erkennen ist, lassen sich verschiedene, durch Knicke in der p,v,T-Fläche abgegrenzte Bereiche unterscheiden. Neben den Einphasengebieten – das sind die Flächen, auf denen der Stoff gasförmig, flüssig oder fest vorliegt – gibt es Gebiete, in denen zwei Phasen gleichzeitig vorhanden sind. Bei diesen so genannten Zweiphasengebieten handelt es sich um das Nassdampfgebiet (hier sind Gas und Flüssigkeit im Gleichgewicht), das Schmelzgebiet (Gleichgewicht zwischen Festkörper und Flüssigkeit) und das Sublimationsgebiet (Gleichgewicht zwischen Festkörper und Gas). Die Grenzlinien zwischen den einzelnen Gebieten tragen unterschiedliche Bezeichnungen. So heißt z. B. die Linie zwischen dem Gebiet des Festkörpers und dem Schmelzgebiet Schmelzlinie und diejenige zwischen dem Schmelzgebiet und dem Gebiet der Flüssigkeit Erstarrungslinie. Das Gebiet der Flüssigkeit ist vom Nassdampfgebiet durch die Siedelinie und das Nassdampfgebiet vom Gebiet der Gasphase durch die Kondensationslinie (Taulinie) getrennt. Die Siedelinie und die Kondensationslinie laufen mit steigenden Drücken und Temperaturen aufeinander zu und treffen sich im so genannten kritischen Punkt K. Die Isotherme und die Isobare, die durch diesen Punkt laufen, werden als kritische Isotherme T = Tk und als kritische Isobare p = pk bezeichnet. Die kritische Temperatur Tk, der kritische Druck pk und das kritische spezifische Volumen vk sind für jeden realen Stoff charakteristische Größen. 116 5 2 3 4 1 Abb. 6.1: p,v,T-Fläche eines reinen realen Stoffes (vgl. Baehr, 1973, S. 158) Die in Abb. 6.1 eingezeichnete Zustandsänderung führt auf einer Linie p = konst. vom Gebiet der Flüssigkeit (1) durch das Nassdampfgebiet bis ins Gebiet der Gasphase (5). Sie wird durch Zufuhr von Wärme verursacht und läuft folgendermaßen ab: (1) → (2): Erwärmung der Flüssigkeit bei konstantem Druck: Die Temperatur steigt an, das spezifische Volumen nimmt leicht zu. Im Zustandspunkt (2) wird die Siedelinie erreicht. (2) → (4): Weitere Wärmezufuhr, dabei Durchquerung des Nassdampfgebietes: Die Flüssigkeit siedet, und es bildet sich Dampf. Im Zustandspunkt (3) ist etwa die Hälfte der Flüssigkeit verdampft. Bei konstantem Druck bleibt während des Verdampfungsvorgangs auch die Temperatur konstant (Siedetemperatur). Das spezifische Volumen nimmt stark zu. Im Zustandspunkt (4) wird die Kondensationslinie erreicht. Der Stoff besteht nun vollständig aus Dampf (Gas). 117 (4) → (5): Weitere Wärmezufuhr bei konstantem Druck: Die Temperatur steigt nun wieder an, das spezifische Volumen nimmt weiter zu, allerdings nicht mehr so stark wie im Nassdampfgebiet. Abb. 6.2: p,v-Diagramm eines realen Stoffes mit den Grenzkurven der Zweiphasengebiete und den Isothermen T = konst. (Baehr, 1973, S.160) Eine ebene Darstellung der p,v,T-Fläche aus Abb. 6.1 erhält man im p,v-Diagramm, Abb. 6.2. Es entsteht durch Projektion der p,v,T-Fläche auf die p,v-Ebene und enthält neben den Grenzkurven der Zustandsgebiete die Isothermen T = konst. als Parameterlinien. Die Isothermen fallen im Nassdampfgebiet, im Schmelzgebiet und im Sublimationsgebiet mit den Isobaren zusammen, laufen dort somit horizontal. Projiziert man die p,v,T-Fläche auf die p,T-Ebene, so erhält man das p,T-Diagramm, Abb. 6.3. Hierin lassen sich wieder die Gebiete des Festkörpers, der Flüssigkeit und der Gasphase unterscheiden. Sie sind in diesem Diagramm durch die Schmelzdruckkurve, die Dampfdruckkurve und die Sublimationsdruckkurve voneinander getrennt. Die Schmelzdruckkurve entsteht aus der Schmelzlinie und der Erstarrungslinie des p,v,T-Diagramms. Durch die Projektion fallen die beiden Linien im p,TDiagramm zusammen. Ebenso vereinen sich im p,T-Diagramm die Siedelinie und die Kondensationslinie zur Dampfdruckkurve sowie die Sublimations- und Desublimationslinie zur Sublimationsdruckkurve. 118 Abb. 6.3: p,T-Diagramm eines realen Stoffes mit den Grenzkurven der drei Phasen und den Isochoren v = konst. (Baehr, 1973, S. 161) Im p,T-Diagramm treffen sich die Dampfdruckkurve, die Schmelzdruckkurve und die Sublimationsdruckkurve in einem Punkt, der als Tripelpunkt bezeichnet wird. Er ist die Projektion der Tripellinie aus dem p,v,T-Diagramm und entspricht jenem einzigen Zustand, in dem alle drei Phasen eines realen Stoffes — Gasphase, Flüssigkeit und Festkörper — miteinander im thermodynamischen Gleichgewicht stehen. Für Wasser liegt dieser Zustand bei Ttr = 273,16 K und ptr = 6,11⋅10-3 bar. Die Dampfdruckkurve endet im kritischen Punkt K, weil sich hier die Siede- und die Kondensationslinie treffen. Bei höheren Drücken als dem kritischen Druck wird das Gebiet der Flüssigkeit von dem der Gasphase formal durch die kritische Isotherme getrennt. Eine scharf definierte Grenze existiert allerdings nicht. Die Flüssigkeit geht dort praktisch unmerklich in die Gasphase über; man spricht von Phasenkontinuität. 6.2 Thermische Zustandsgleichungen für Feststoffe und Flüssigkeiten Die Zustandsfläche eines realen Stoffes lässt sich aufgrund ihrer Komplexität nicht mehr mit einer einzigen thermischen Zustandsgleichung beschreiben. Deshalb müssen für jedes der Zustandsgebiete auf der p,v,T-Fläche eigene Gleichungen formuliert werden. Alle diese Gleichungen sind recht kompliziert und nur mit Computerprogrammen handhabbar. Mit ihrer Hilfe hat man die Zustandsgrößen für technisch wichtige Stoffe in weiten Temperatur- und Druckbereichen berechnet und in Tafeln zusammengestellt. Lediglich für den Bereich der Feststoffe und näherungsweise für Flüssigkeiten lassen sich praktikable thermische Zustandsgleichungen formulieren. 119 Feststoffe — Das Zustandsgebiet des Festkörpers liegt auf der Zustandsfläche des p,v,T-Diagramms bei kleinen spezifischen Volumina, Abb. 6.1. In diesem Bereich ändert sich das spezifische Volumen selbst bei großen Druckänderungen kaum. Lediglich bei Zunahme der Temperatur ist erfahrungsgemäß eine Ausdehnung des Festkörpers, d. h. ein Anstieg seines Volumens und damit auch seines spezifischen Volumens zu verzeichnen. Geht man von einem Bezugsvolumen V0 bei der Temperatur t0 aus, so lässt sich die Abhängigkeit des Volumens V von der Temperatur t näherungsweise durch folgende lineare Beziehung beschreiben: V [ = V ( t ) = V0 1 + β 0 ⋅ ( t − t 0 )] (Gl. 6.1) In dieser Gleichung ist der Proportionalitätsfaktor β0 der thermische Volumenausdehnungskoeffizient des betreffenden Stoffes. Er muss experimentell bestimmt werden und ist abhängig von der jeweiligen Bezugstemperatur t0. In vielen technischen Fällen ist nur die Dehnung in einer Koordinatenrichtung von Interesse. Zu diesen Zweck kann Gl. 6.1 eindimensional geschrieben werden: L = [ ] L0 1 + α 0 ⋅ ( t − t 0 ) (Gl. 6.2) Hierin ist L0 die Bauteillänge bei der Bezugstemperatur t0 und L die Länge des Bauteils bei der Temperatur t. Der Proportionalitätsfaktor α0 ist der von der Bezugstemperatur t0 abhängige lineare Ausdehnungskoeffizient. Für einen isotropen Festkörper gilt der Zusammenhang α0 = 1/3 β0. Flüssigkeiten — Für reale Flüssigkeiten ändert sich das Volumen nicht nur bei einer Zu- oder Abnahme der Temperatur. Auch bei einer Zu- oder Abnahme des Druckes ist eine geringfügige Veränderung des Volumens zu verzeichnen. Da die Zustandsfläche des Flüssigkeitsgebietes für Drücke p < pk und Temperaturen T < Tk in weiten Bereichen nur schwach gekrümmt ist, siehe Abb. 6.1, kann das Zustandsverhalten der Flüssigkeit in diesem Bereich durch einen linearen Ansatz beschrieben werden. Zu diesem Zweck wird die für den Festkörper gültige Gl. 6.1 um einen Ausdruck erweitert, der die Abhängigkeit des Volumens vom Druck berücksichtigt: V [ = V ( t , p ) = V0 1 + β 0 ⋅ (t − t 0 ) − k 0 ⋅ ( p − p 0 )] (Gl. 6.3) In Gl. 6.3 ist k0 der für den Referenzpunkt geltende isotherme Kompressibilitätskoeffizient. Er muss für jede Flüssigkeit experimentell bestimmt werden, hängt aber vom Druck praktisch nicht und im Gegensatz zum thermischen Volumenausdehnungskoeffizienten β0 von der Temperatur nur geringfügig ab (vgl. Baehr, 1973, S.194). 120 6.3 Der isobare Verdampfungsvorgang Der Phasenübergang Flüssigkeit — Dampf und das zweiphasige Nassdampfgebiet haben große technische Bedeutung. Deshalb wird zur Verdeutlichung der in Abschn. 6.2 kurz angesprochene Phasenübergang bei konstantem Druck am Beispiel von 1 kg Wasser näher betrachtet. Das Wasser befindet sich zu diesem Zweck in einem beheizbaren Zylinder, der durch einen frei verschiebbaren Kolben verschlossen ist, Abb. 6.4. Der Kolben dichtet das System zur Umgebung hin ab und verhindert die Vermischung von Wasserdampf und Umgebungsluft. Abb. 6.4: Verdampfung bei konstantem Druck Im Ausgangszustand (1) liegt das Wasser in der flüssigen Phase vor. Bei Erwärmung steigt die Temperatur bei lediglich geringer Volumenausdehnung. Ab einer bestimmten Temperatur, die bei einem Druck von p = 1,0 bar bei ts = 99,63 °C liegt, bilden sich die ersten Dampfblasen, und das Wasser beginnt zu sieden, Zustandspunkt (2). Das spezifische Volumen der flüssigen Phase bei Siedebeginn wird mit v’ bezeichnet. Bei weiterer Wärmezufuhr bilden sich immer mehr Dampfblasen am beheizten Zylinderboden. Sie steigen in der siedenden Flüssigkeit auf und führen zu einem wachsenden Dampfvolumen unter dem Kolben, Zustand (3). Der während des Verdampfungsvorgangs im Phasengleichgewicht mit der siedenden Flüssigkeit stehende Dampf wird als gesättigter Dampf oder als Sattdampf und das heterogene Gemisch aus siedender Flüssigkeit und gesättigtem Dampf als Nassdampf bezeichnet. Die Temperatur liegt während des Phasenübergangs konstant bei ts = 99,63 °C. Das spezifische Volumen vx des Nassdampfes nimmt jedoch erheblich zu. 121 Im Zustandspunkt (4) ist der Verdampfungsvorgang gerade abgeschlossen und der letzte Flüssigkeitstropfen verschwunden. Das System besteht nun vollständig aus gesättigtem Dampf. Sein spezifisches Volumen wird mit v’’ bezeichnet. Wird der Sattdampf vom Zustandspunkt (4) aus weiter erwärmt, so steigt seine Temperatur bei gleichzeitiger Volumenzunahme weiter an. Man spricht nun von überhitztem Dampf oder von Heißdampf, was lediglich eine andere Bezeichnung für die Gasphase ist. Der beschriebene Prozess kann auch in umgekehrter Richtung ablaufen, wenn man dem Dampf ausgehend vom Zustand (5) Wärme entzieht. Im Zustandspunkt (4) wird dann der erste Flüssigkeitstropfen auftreten und im Zustand (2) die letzte Dampfblase kondensieren. Sowohl der Verdampfungsprozess als auch der Kondensationsprozess durchlaufen die gleichen Werte der thermischen Zustandsgrößen. Auch die Beträge der beim Verdampfungsprozess zu- bzw. beim Kondensationsprozess abzuführenden Wärmen sind gleich. 122 6.4 Die Zustandsgrößen im Nassdampfgebiet Bei der Verdampfung einer Flüssigkeit unter konstantem Druck bleibt, wie wir wissen, die Siedetemperatur der Flüssigkeit konstant. Die Höhe dieser Temperatur hängt von dem Druck ab, bei dem das Sieden bzw. die Verdampfung stattfindet. Zu jeder Siedetemperatur gehört ein ganz bestimmter Siededruck, tS = tS(pS), bzw. umgekehrt. Ebenso ist das spezifische Volumen der siedenden Flüssigkeit und das des Sattdampfes von diesem Druck abhängig, v’ = v’(pS) bzw. v’’ = v’’(pS). Für Wasser findet man diese Größen in den so genannten Dampftafeln tabelliert, siehe Abschn. 6.5. Abb. 6.5: Isobarer Verdampfungsprozess im p,v-Diagramm Da im Nassdampfgebiet die siedende Flüssigkeit und der Sattdampf im Gleichgewicht nebeneinander auftreten, benötigt man zur Beschreibung der Systemzusammensetzung eine geeignete zusätzliche Größe. Hierzu wird der relative Massenanteil des während des Verdampfungsprozesses aktuell vorhandenen Sattdampfes herangezogen. Er wird als Dampfgehalt x bezeichnet und ist nur im Nassdampfgebiet definiert: x = m '' m ' + m '' (G. 6.4) Entsprechend lässt sich der als Flüssigkeitsgehalt bezeichnete relative Massenanteil der aktuell vorhandenen siedenden Flüssigkeit berechnen: y = 1− x = m' m ' + m '' (Gl. 6.5) 123 Auf der Siedelinie gilt x = 0 wegen m’’ = 0, und auf der Kondensationslinie ist x = 1 wegen m’ = 0. Aufgrund dieses Zusammenhangs ist im p,v-Diagramm der Abb. 6.5 die Siedelinie mit x = 0 und die Kondensationslinie mit x = 1 bezeichnet. Neben diesen beiden Grenzlinien sind dort weitere Linien konstanten Dampfgehaltes x = konst. mit 0 < x < 1 eingetragen. Den Dampfgehalt x findet man auch unter den Darstellungen der Abb. 6.4 angegeben. Mithilfe des Dampfgehaltes x kann nun das spezifische Volumen des Nassdampfes berechnet werden. Für das extensive Volumen gilt: Vx = V ' + V '' = m '⋅ v ' + m ''⋅ v '' und für das spezifische Volumen: vx = Vx mx = m '⋅ v ' + m ''⋅ v '' m ' + m '' = m' m '' ⋅ v' + ⋅ v '' m ' + m '' m ' + m '' Somit folgt für das spezifische Volumen vx = (1 − x) ⋅ v ' + x ⋅ v '' (Gl. 6.6) bzw. nach kurzer Umformung vx = v ' + x ⋅ ( v '' − v ') (Gl. 6.7) Ebenso wie das spezifische Volumen des Nassdampfes lassen sich die spezifische Enthalpie und die spezifische Entropie von Nassdampf berechnen. Allerdings müssen hierzu die Werte der spezifischen Enthalpie und der spezifischen Entropie auf der Siedelinie, h’ und s’, bzw. auf der Kondensationslinie, h’’ und s’’, bekannt sein. Für die siedende Flüssigkeit werden diese Werte wieder mit einem Strich und für den gesättigten Dampf gleicher Temperatur und gleichen Drucks mit zwei Strichen gekennzeichnet. Für Wasser findet man diese Größen wieder als Funktion des Siededrucks, z. B. h’ = h’(ts), in den Dampftafeln tabelliert, siehe Abschn. 6.5. Dann gilt hx = (1 − x ) ⋅ h ' + = (1 − x) ⋅ s ' + x ⋅ s '' = s ' + x ⋅ ( s '' − s ') x ⋅ h '' = h ' + x ⋅ ( h '' − h ') (Gl. 6.8) und sx (Gl. 6.9) Die Differenz der spezifischen Enthalpien von gesättigtem Dampf und siedender Flüssigkeit bei gleichem Druck und gleicher Temperatur nennt man die spezifische Verdampfungsenthalpie ∆hV. Beim Wasser wird die spezifische Verdampfungsenthalpie aus historischen Gründen mit r bezeichnet. Somit ist ∆hV ( bzw. r) = h '' − h ' (Gl. 6.10) 124 Die spezifische Verdampfungsenthalpie ist identisch mit der spezifischen Wärme q, die erforderlich ist, um 1 kg einer Flüssigkeit bei konstantem Druck vom Zustand x = 0 bis zum Zustand x = 1 zu verdampfen. Die spezifische Verdampfungsenthalpie hängt in einfacher Weise mit der spezifischen Verdampfungsentropie zusammen. Aufgrund der bei konstantem Druck ebenfalls konstanten Temperatur im Nassdampfgebiet gilt ∆hV ( bzw. r) = h '' − h ' = TS ⋅ ( s '' − s ') (Gl. 6.11) Man beachte, dass es sich in Gl. 6.11 bei Ts um die Thermodynamische Temperatur und nicht um die CELSIUS-Temperatur handelt. Für die Berechnung von Verdampfungsprozessen in geschlossenen Systemen wird bei der Anwendung des ersten Hauptsatzes die Änderung der spezifischen inneren Energie bei der Verdampfung benötigt. Sie lässt sich mithilfe der bekannten Definitionsgleichung der spezifischen Enthalpie, h = u + p⋅v, wie folgt ermitteln: u '' − u ' = h '' − h ' − p ⋅ ( v '' − v ') 6.5 (Gl. 6.12) Die Zustandstafeln für Wasser Wie bereits in Abschn. 6.3 erwähnt, lässt sich das Zustandsverhalten der realen Stoffe für die einzelnen Phasengebiete nicht in einfacher Weise durch leicht handhabbare Gleichungen beschreiben. Aus diesem Grund werden dem Anwender die Zustandsgrößen der realen Stoffe in Form von Tabellen zur Verfügung gestellt. Derartige Zustandtafeln gibt es für technisch wichtige Stoffe, so auch für Wasser. Die Zustandstafeln für Wasser werden aus historischen Gründen auch als Wasserdampftafeln oder einfach als Dampftafeln bezeichnet. Diese Tafeln enthalten zwei Gruppen von Tabellen, die Tafeln für das Nassdampfgebiet und die Tafeln für die homogenen Gebiete Flüssigkeit und Dampf. Tafeln für das Nassdampfgebiet (Nassdampftafeln) mit dem Druck oder der Temperatur als der einzigen unabhängigen Zustandsgröße: a) Nassdampf-Drucktafel: Sie enthält in Abhängigkeit vom Druck Werte der Siedebzw. Sättigungstemperatur ts(p) sowie Werte des spezifischen Volumens, der spezifischen Enthalpie und der spezifischen Entropie auf der Siedelinie und der Kondensationslinie, also die Funktionen v’(p), v’’(p), h’(p), h’’(p), s’(p) und s’’(p). Zusätzlich findet man Werte der spezifischen Verdampfungsenthalpie r(p). Ein Auszug aus der Nassdampf-Drucktafel für Wasser ist in Tab. 6.1 zu sehen. 125 p ts v’ v’’ h’ h’’ r s’ s’’ bar °C m³/kg m³/kg kJ/kg kJ/kg kJ/kg kJ/(kg K) kJ/(kg K) 0,01 6,98 0,00100 129,209 29,3 2514,4 2485,0 0,1060 8,9767 0,10 45,83 0,00101 14,6746 191,8 2584,8 2392,9 0,6493 8,1511 1,00 99,63 0,00104 1,69373 417,5 2675,4 2257,9 1,3027 7,3598 5,00 151,84 0,00109 0,37468 640,1 2747,5 2107,4 1,8604 6.8192 10,00 179,88 0,00113 0,19429 762,6 2776,2 2013,6 2,1382 6,5828 20,00 212,37 0,00118 0,09954 908,6 2797,2 1888,6 2,4469 6,3367 50,00 263,91 0,00129 0,39429 1154,5 2794,2 1639,7 2,9206 5,9735 100,00 310,96 0,00145 0,01804 1408,0 2727,7 1319,7 3,3605 5,6198 150.00 342,13 0,00166 0,10340 1611,0 2615,0 1004,0 3,6859 5,3178 200.00 365,70 0,00204 0,00588 1826,5 2418,4 591,9 4,0149 4,9412 221,20 374,15 0,00317 0,00317 2107,4 2107,4 0,0 4,4429 4,4429 Tab. 6.1: Grober Auszug aus der Nassdampf-Drucktafel b) Nassdampf-Temperaturtafel: Sie enthält in Abhängigkeit von der Temperatur Werte des Dampf- bzw. Sättigungsdrucks ps(t) und die Funktionen v’(t), v’’(t), h’(t), h’’(t), s’(t), s’’(t) und r(t). Ein Auszug aus dieser Tafel ist in Tab. 6.2 dargestellt. Sowohl die Nassdampf-Temperaturtafel als auch die Nassdampf-Drucktafel enthalten dieselben Informationen, da sie dasselbe Zustandsgebiet beschreiben. t ps v’ v’’ h’ h’’ r s’ s’’ °C bar m³/kg m³/kg kJ/kg kJ/kg kJ/kg kJ/(kg K) kJ/(kg K) 0,01 0,0061 0,00100 206,162 0,0 2501,6 2501,6 0,0000 9,1575 50,00 0,1234 0,00101 12,0457 209,3 2592,2 2382,9 0,7035 8,0776 100,00 1,013 0,00104 1,67299 419,1 2676,0 2256,9 1,3069 7,3554 150,00 4,75 0,00109 0,39245 632,1 2745,4 2113,2 1,8416 6,8358 200,00 15,55 0,00116 0,12716 852,4 2790,9 1938,6 2,3307 6,4278 250,00 39,78 0,00125 0,05004 1085,8 2800,4 1714,7 2,7935 6,0708 300,00 85,93 0,00140 0,02165 1345,1 2751,0 1406,0 3,2552 5,7081 330,00 128,63 0,00156 0,01299 1526,5 2670,2 1143,6 3,5528 5,4490 350,00 165,35 0,00174 0,00880 1671,9 2567,7 895,7 3,7800 5,2177 370,00 210,54 0,00221 0,00497 1890,2 2342,8 452,6 4,1108 4,8144 374,15 221,20 0,00317 0,00317 2107,4 2107,4 0,0 4,4429 4,4429 Tab. 6.2: Grober Auszug aus der Nassdampf-Temperaturtafel 126 Nullpunktvereinbarung — Für die spezifische Enthalpie und die spezifische Entropie lassen sich keine Absolutwerte sondern lediglich Differenzen angeben. Zur tabellarischen Darstellung dieser Zustandgrößen in Abhängigkeit von der Temperatur und vom Druck muss deshalb ein Nullpunkt festgelegt werden. Für die Wasserdampftafeln hat man als Nullpunkt den Tripelpunkt des Wassers vereinbart. Für t = ttr = 0,01 °C und für p = ptr = 6,11 ⋅ 10-3 bar gilt damit h(t,p) = 0 und s(t,p) = 0. Tafeln für die homogenen Zustandsgebiete (Gas und Flüssigkeit) mit dem Druck und der Temperatur als den unabhängigen Zustandsgrößen: In diesen Tafeln sind die Angaben nach Isobaren p = konst. über einen weiten Druckbereich geordnet. Für jede tabellierte Isobare findet man in Abhängigkeit von diskreten Werten der Temperatur Werte von v, h und s. Tab. 6.3 zeigt ein Beispiel für die Isobaren p = 7,5 bar und p = 10,0 bar. t p = 7,5 bar p = ts= 167,76 °C °C 10,0 bar ts = 179,88 °C v h s v h s m³/kg kJ/kg kJ/(kg K) m³/kg kJ/kg kJ/(kg K) v’ = h’ = 0,001112 v’’ = s’ = 709,3 h’’ = v’ = 2,020 h’ = 0,001127 v’’ = s’’ = s’ = 762,6 h’’ = 2,138 s’’ = 0,255427 2764,8 6,682 0,194293 2776,2 6,583 0 0,001000 0,8 0.000 0,001000 1,0 0.000 5 0,001000 21,8 0.076 0,001000 22,0 0,076 10 0,001000 42,7 0.151 0,001000 43,0 0.151 15 0,001000 63,7 0.224 0,001000 63,9 0.224 20 0,001001 84,6 0,296 0,001001 84,8 0,296 : : 100 : 0,001043 : 419,6 1,306 0,001043 419,7 1,306 125 0,001065 525,3 1,581 0,001065 525,5 1,581 150 0,001091 632,3 1,841 0,001090 632,5 1,841 175 0,260884 2782,5 6,721 0,001121 741,1 2,091 200 0,279055 2841,4 6,849 0,205918 2826,1 6,692 225 0,296462 2897,7 6,965 0,219617 2886,2 6,815 250 0,313355 2952,2 7,072 0,232748 2943,0 6,926 : : : : 800 0,659385 8,633 0,494296 Tab. 6.3: : : 4155,2 : : 4154,1 : : 8,500 Auszug aus den Wasserdampftafeln für die homogenen Gebiete Flüssigkeit und überhitzter Dampf 127 In den Tafeln ist das Gebiet der Flüssigkeit von dem des überhitzten Dampfes (Gasphase) durch waagerecht durch das Zahlenfeld verlaufende Linien getrennt. Beispielsweise liegt für p = 7,5 bar diese Linie zwischen den Temperaturen 150 und 175 °C, siehe Tab. 6.3. Hinter diesen Linie verbirgt sich das gesamte Nassdampfgebiet. Somit liegt die Trennlinie für p = 7,5 bar exakt bei der Siedetemperatur ts(7,5 bar) = 167,76 °C. Nähert man sich der Trennlinie von der Flüssigkeitsseite, d. h. von den niedrigeren Temperaturen her, dann erreicht man die Siedelinie mit den Werten v’, h’ und s’. Nähert man sich der Tennlinie dagegen von der Heißdampfseite, d. h. von den höheren Temperaturen her, dann erreicht man die Kondensationslinie mit den Werten v’’, h’’ und s’’. Es ist nicht nötig, die Werte für ts, v’, v’’, h’, h’’, s’ und s’’ in den Nassdampftafeln nachzuschlagen; man findet sie für jede Isobare im Kopf der Tabellen für die homogenen Zustandsgebiete. Gegebenenfalls muss man beim Gebrauch der Tafeln für die homogene Zustandsgebiete zweifach, d. h. in Richtung p und in Richtung t interpolieren, um die Werte für v(p,t), h(p,t) und s(t,p) zu erhalten. Bei Interpolationen für p = konst. in t-Richtung ist darauf zu achten, dass in der Tabelle die Trennlinie zwischen dem Flüssigkeitsbereich- und dem Bereich des überhitzten Dampfes nicht überschritten wird. Es darf immer nur bis an die Trennlinie, d. h. bis an die Siedelinie bzw. die Kondensationslinie, heran interpoliert werden. Beispiel 6.1: Ein ölgefeuerter Flammrohr-Rauchrohr-Kessel zur Versorgung eines Krankenhauses mit Sattdampf wird zum Anfahren vorbereitet. Der Kessel hat einen Wasserraum-Inhalt von 12 m³, der im Zustand (1) zu 75 % mit siedendem Wasser und zu 25 % mit Sattdampf gefüllt ist. Der Druck beträgt p1 = 2 bar. Eine Zufuhr von Speisewasser und eine Entnahme von Sattdampf findet nicht statt. Durch Inbetriebnahme des Brenners wird dem Kessel Wärme zugeführt. Das Kesselwasser wird aufgeheizt, und der Druck steigt an. Nach Erreichen von p2 = 16 bar wird der Brenner wieder abgeschaltet. Für Berechnungen steht mit Tab. 6.4 ein Auszug aus den Wasserdampf-Tafeln zur Verfügung. 128 p ts vI v II hI h II bar °C m³/kg m³/kg kJ/kg kJ/kg 2,0 120,230 0,0010608 0,885441 504,7 2706,3 4,0 143,623 0,0010839 0,462224 604,7 2737,6 6,0 158,837 0,0011009 0,315473 670,4 2755,5 8,0 170,414 0,0011150 0,240257 720,9 2767,5 10,0 179,884 0,0011274 0,194292 762,6 2776,2 12,0 187,961 0,0011386 0,163200 798,4 2782,7 14,0 195,042 0,0011489 0,140721 830,1 2787,8 16,0 201,371 0,0011586 0,123686 858,6 2791,7 18,0 207,111 0,0011678 0,110317 884,6 2794,8 20,0 212,374 0,0011766 0,099536 908,6 2797,2 Tab. 6.4: Wasserdampf-Tafel für das Nassdampfgebiet (Auszug) Zu berechnen ist: a) für den Zustand (1) der Dampfgehalt x1, das spezifische Volumen v1 und die spezifische Enthalpie h1, b) für den Zustand (2) der Dampfgehalt x2, das spezifische Volumen v2 und die spezifische Enthalpie h2, c) die Wärme Q12, die dem Kessel während der Aufheizphase zugeführt wird, d) die erforderliche Brennstoffmasse mB, wenn Heizöl mit einem spezifischen Heizwert von Hu = 42 MJ/kg zum Einsatz kommt und der Kesselwirkungsgrad ηK = 0,9 beträgt. Zu a): Im Zustand (1) ist das siedende Kesselwasser mit dem Sattdampf im thermodynamischen Gleichgewicht. Es liegt Nassdampf vor. In der Nassdampf-Drucktafel findet man für p1 = 2 bar: ts,1 = ts(2 bar) = 120,23 °C vI1 = vI(2 bar) = 0,0010608 m³/kg hI1 = hI(2 bar) = 504,7 kJ/kg vII1 = vII (2 bar) = 0,885441 m³/kg hII1 = hII (2 bar) = 2706,3 kJ/kg 129 Nun gilt: VI 1 = VII1 = 0,75 ⋅ V = 0,25 ⋅ V = 0,75 ⋅ 12 m³ = 0,25 ⋅ 12 m³ = 9 m³ 3 m³ und v '1 v ''1 = V '1 m '1 = V ''1 m ''1 m '1 V '1 = v '1 → m ''1 V ''1 = v ''1 → = 9 m3 0,0010608 m 3 / kg = 3 m3 0,885441 m 3 / kg = 8484,16 kg = 3,39 kg Die Gesamtwassermasse im Kessel ist somit: m = m '1 + m ''1 = 8484,16 kg + 3,39 kg = 8487,55 kg Damit berechnet sich der Dampfgehalt im Zustand (1) zu x1 = m ''1 m = 3,39 kg 8487,55 kg = 0,0004 kg Sattdampf kg Wasser Für das spezifische Volumen im Zustand (1) gilt. 12 m 3 8487,55 kg V = m v1 = v1 = v '1 + v1 = 0,0010608 = m3 0,001414 kg oder auch x1 ⋅ ( v ''1 − v '1 ) m3 m3 + 0,0004 ⋅ ( 0,885441 − 0,0010608) kg kg = 0,001414 m3 kg Analog ergibt sich die spezifische Enthalpie im Zustand (1): h1 = h '1 + h1 = 504,7 kJ kg x1 ⋅ ( h ''1 − h '1 ) + 0,0004 ⋅ ( 2706,3 − 504,7) kJ kg = 505,6 kJ kg Zu b): Auch im Zustand (2) ist das siedende Kesselwasser mit dem Sattdampf im thermodynamischen Gleichgewicht. Jedoch befindet sich das System nun auf einem höheren Druckniveau, wodurch sich sämtliche Werte vI, vII sowie hI und hII verändert haben. In der Nassdampf-Drucktafel findet man für p2 = 16 bar: ts,2 = ts(16 bar) = 201,37 °C vI2 = vI(16 bar) = 0,0011586 m³/kg vII2 = vII (16 bar) = 0,123686 m³/kg hI2 = hI(16 bar) = 858,6 kJ/kg hII2 = hII (16 bar) = 2791,7 kJ/kg 130 Während der Zustandsänderung (1) > (2) wird kein Speisewasser zugeführt und kein Sattdampf entnommen. Das Volumen des Wasserdampfsystems im Kessel bleibt konstant, die Zustandsänderung ist isochor. Es gilt somit v2 = v1 = v = 0,001414 m³/kg. Da der Zustandspunkt (2) im Nassdampfgebiet liegt, gilt analog zum Zustandspunkt (1): v2 = v '2 + x 2 ⋅ ( v '' 2 − v ' 2 ) , woraus sich der Dampfgehalt im Zustand (2) berechnen lässt: x2 = v2 − v '2 v '' 2 − v ' 2 x2 = ( 0,001414 − 0,0011586) m 3 kg ( 0,123586 − 0,0011586) m 3 kg = 0,0021 kg Sattdampf kg Wasser Mit dem Dampfgehalt x2 folgt für die spezifische Enthalpie im Zustand (2): h2 = h '2 + h2 = 858,6 kJ kg x 2 ⋅ ( h '' 2 − h ' 2 ) + 0,0021 ⋅ ( 2791,7 − 858, 6) kJ kg = 862,7 kJ kg Zu c): Die während der isochoren Zustandsänderung (1) > (2) zugeführte Wärme ergibt sich aus dem 1. Hauptsatz für geschlossene Systeme: Q12 = m ⋅ ( u2 − u1 ) Q12 = Q12 kJ m3 kJ = 8487,55 kg ⋅ (862,7 − 505,6) − 0,001414 ⋅ (16 − 2) ⋅ 10 2 3 kg kg m Q12 = 8487,55 kg ⋅ (357,1 − 1,98) [ ] m ⋅ h2 − h1 − v ⋅ ( p 2 − p1 ) kJ kg = 3014099 kJ = 3014,1 MJ Zu d): Der Kesselwirkungsgrad ist ein energetischer Wirkungsgrad. Definiert ist er als Verhältnis von energetischem Nutzen zu energetischem Aufwand. Für ihn gilt stets 0 ≤ ηK ≤ 1. Beim Kessel ist der energetische Nutzen die an das Wasserdampfsystem übergebene Wärme. Der energetische Aufwand ist die in Form von Brennstoff zugeführte Energie. Die Differenz zwischen den beiden Werten ist der energetische Verlust. Das 131 ist die Energie, die vom Kessel in Form von heißem Abgas an die Umgebung abgegeben und deshalb auch als Abgasverlust bezeichnet wird. Es gilt: ηK = Q12 EB mB = Q12 ηK ⋅ Hu 6.6 = Q12 mB ⋅ H u = und somit 3014,1 MJ 0,9 ⋅ 42 MJ kg = 79,74 kg Die kalorischen Zustandsdiagramme T,s-Diagramm — Das T,s-Diagramm eines realen Stoffes zeigt Abb. 6.7. Siedelinie (x = 0) und Kondensationslinie (x = 1) streben zu höheren Temperaturen hin aufeinander zu und bilden im kritischen Punkt ein Maximum. Unterhalb der beiden Grenzkurven liegt das Nassdampfgebiet. Dort gilt auf einer Linie T = konst. auch p = konst.. Abb. 6.7: T,s-Diagramm realer Stoffe (Hahne, 1993, S. 243) Im Nassdampfgebiet verlaufen die Isobaren gemeinsam mit den Isothermen horizontal. Im Flüssigkeitsgebiet, das zwischen der Ordinate T und dem Nassdampfgebiet liegt, steigen die Isobaren mit wachsender spezifischer Entropie s an. Sie liegen dort sehr eng beieinander und schmiegen sich an die Siedelinie an. Im Gasgebiet sind die Isobaren mit wachsendem s progressiv steigende Kurven. 132 Die Isochoren sind im Nassdampfgebiet degressiv steigend, die Linien konstanter spezifischen Enthalpie – die Isenthalpen – degressiv fallend. Im Gasgebiet verlaufen die Isochoren ähnlich wie die Isobaren, sie sind jedoch steiler als diese. Im T,s-Diagramm erscheint die bei einem isobaren Verdampfungsprozess erforderliche spezifische Wärme als Rechteckfläche unter der Zustandsänderungslinie. Da die Zustandsänderungslinie eine Isobare ist, stellt diese Fläche gleichzeitig die spezifische Verdampfungsenthalpie dar. Es gilt: q12 = qV = ∆hV = TS ⋅ ( s '' − s ') (Gl. 6.13) Die spezifische Verdampfungsenthalpie wird deshalb auch als spezifische Verdampfungswärme bezeichnet. Anhand von Abb. 6.7 lässt sich nachvollziehen, dass die Rechteckfläche mit zunehmender Temperatur bzw. zunehmendem Druck immer höher, aber auch immer schmaler wird. Je näher man dem kritischen Punkt K kommt, desto kleiner wird die Fläche. Im kritischen Punkt verschwindet sie schließlich. Dort gilt sI = sII und damit ∆hV = 0. h,s-Diagramm — Das h,s-Diagramm wurde 1904 von R. MOLLIER eingeführt. Durch die Wahl seiner Koordinaten verknüpft es die Aussagen des ersten und zweiten Hauptsatzes. Dabei stellen sich die spezifischen Größen des ersten Hauptsatzes als senkrechte Strecken dar. So lässt sich mithilfe eines Diagramms für Wasserdampf z. B. die technische Arbeit von Dampfturbinen auf einfache Weise bestimmen. K Abb. 6.8: h,s-Diagramm für einen realen Stoff (Hahne, 1993, S. 243) Auch im h,s-Diagramm trennen die Siedelinie und die Kondensationslinie die Zustandsgebiete von Flüssigkeit und Gas vom Nassdampfgebiet. Der kritische Punkt stellt sich allerdings nicht mehr als Maximum der beiden Grenzkurven dar. Er liegt 133 auf dem mit wachsender spezifischer Entropie ansteigenden Ast der Grenzkurven und fällt dort mit deren Wendepunkt zusammen, siehe Abb. 6.8. Die Isobaren schmiegen sich im Flüssigkeitsgebiet sehr nah an die Grenzkurven. Im Heißdampfgebiet sind sie progressiv ansteigende Kurven, die umso steiler verlaufen, je höher der Druck ist. Im Nassdampfgebiet sind die Isobaren ansteigende Geraden. Je höher die Siedetemperatur und damit der zugehörige Dampfdruck ist, desto steiler steigen sie an. Die Isothermen fallen im Nassdampfgebiet mit den Isobaren zusammen. An der Kondensationslinie knicken sie ab und verlaufen im Heißdampfgebiet mit wachsender spezifischer Entropie immer flacher, bis sie in einiger Entfernung von der Kondensationslinie schließlich in die Horizontale übergehen. Für ideale Gase unterscheidet sich das h,s-Diagramm vom T,s-Diagramm nur durch den Ordinatenmaßstab. Da die spezifische Enthalpie idealer Gase nur von der Temperatur und nicht vom Druck abhängt, gilt für T = konst. bei idealen Gasen somit auch h = konst.. log–p,h-Diagramm — Im log–p,h-Diagramm lassen sich isobare Zustandsänderungen besonders einfach darstellen, da die Isobaren horizontale Linien sind. Der Druck ist logarithmisch aufgetragen, um einen größeren Druckbereich zu Abb. 6.9: log–p,h-Diagramm eines realen Stoffes (Baehr, 1973, S. 190) erfassen. Abb. 6.9 zeigt den typischen Aufbau eines log–p,h-Diagramms mit den Zustandsgebieten der reinen Phasen und dem Nassdampfgebiet. Neben den Isothermen enthält es noch die Isentropen als Parameterlinien, womit es dem h,sDiagramm praktisch gleichwertig ist. 134 Das Diagramm ist für Prozesse der Kältetechnik von besonderem Interesse. Sowohl die Verdampfung eines Kältemittels, z. B. im Kühlaggregat eines Kühlschranks, als auch seine Rückkühlung und Kondensation, z. B. im Wärmeübertrager auf der Rückseite eines Kühlschranks, verlaufen nahezu isobar. Die dabei umgesetzten Wärmen lassen sich in dem Diagramm als waagerechte Strecken ablesen. Kontrollfragen 6.1 Warum kann ein realer Stoff nicht mit der thermischen Zustandsgleichung des idealen Gases beschrieben werden? 6.2 In welchem Aggregatzustand liegt ein reiner Stoff im Tripelpunkt vor? 6.3 Wodurch unterscheidet sich Sattdampf von Nassdampf? 6.4 Wie groß ist der Dampfgehalt für Sattdampf? 6.5 Was stellt die spezifische Verdampfungsenthalpie eines Stoffes anschaulich dar? 6.6 Wie groß ist die Verdampfungsenthalpie im kritischen Punkt? 135 Übungsaufgaben 6.1 Für eine Wärmebehandlung wird ein erhitzter Stahl in ein offenes Ölbad von VÖl,1 = 0,2 m³ getaucht, dessen Druck überall mit dem Umgebungsdruck von pamb = 1 bar identisch ist. Das Ölbad dehnt sich dabei bis auf VÖl,2 aus, und seine Temperatur steigt von tÖl,1 = 20°C bis auf tÖl,2 = 70°C an. Der thermische Volumenausdehnungkoeffizient des Öls beträgt βÖl = 850 · 10-6 m³/(m³ K). Welches Volumen VÖl,2 in m³ nimmt das Ölbad nach der Erwärmung durch den Stahl ein? 6.2 Die Beheizung der Montagehalle eines Industriebetriebes erfolgt mit einem dampfbetriebenen Lufterhitzer: • Dem Apparat werden hierzu V 1 = 150000 m³/h Luft aus der Umgebung zugeführt. Er erwärmt sie bei konstantem Druck von p = 1 bar von t1 = 20 °C auf t2 = 60 °C: Der Heizdampf steht vor dem Regelventil mit p3 = 3 bar und t3 = 150 °C zur Verfügung. Er wird im Lufterhitzer bei p = 2 bar kondensiert. Das Kondensat verlässt den Apparat um 20 K unterkühlt (d. h., seine Temperatur liegt 20 K unter der Siedetemperatur). Alle Anlagenteile seien nach außen adiabat, äußere Energien sind zu vernachlässigen! a) Geben Sie die Temperatur t4 des abströmenden Kondensates in °C und seine spezifische Enthalpie h4 an. • b) Berechnen Sie den Luftmassenstrom m L . • c) Welchen Wärmestrom Q 12 nimmt die Luft auf? • d) Wie groß ist der erforderliche Massenstrom m D des Heizdampfes? 136