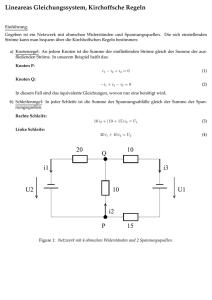
Lineare Algebra
Werbung

Günter M. Gramlich Mathematik-Studienhilfen Lineare Algebra Eine Einführung 2., aktualisierte Auflage Inhaltsverzeichnis 1 Lineare Gleichungssysteme und Matrizen 1.1 Lineare Gleichungssysteme . . . . . . . . . . . . . . . . 1.2 Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . 1.3 Elementare Umformungen und Zeilenstufenformen . . 1.4 Das Gauß- und Gauß-Jordan-Verfahren . . . . . . 1.5 Mehr uber Matrizen . . . . . . . . . . . . . . . . . . . ¨ 1.6 Operationen mit Matrizen . . . . . . . . . . . . . . . . 1.7 Die Matrixform eines linearen Gleichungssystems . . . 1.8 Losen quadratischer Systeme durch Matrixinvertierung ¨ 1.9 Weitere Bemerkungen und Hinweise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 9 12 13 16 22 24 37 38 45 2 Vektoren in der Ebene und im Raum 2.1 Geometrische Vektoren . . . . . . . . . . . . . . . . . . 2.2 Vektoren in Koordinatensystemen . . . . . . . . . . . 2.3 Rechenregeln fur ¨ Vektoren in Koordinatendarstellung 2.4 Die Lange von Vektoren . . . . . . . . . . . . . . . . . ¨ 2.5 Das Skalarprodukt . . . . . . . . . . . . . . . . . . . . 2.6 Das Kreuzprodukt . . . . . . . . . . . . . . . . . . . . 2.7 Weitere Bemerkungen und Hinweise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 48 52 57 58 60 69 73 Ebenen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76 76 79 86 3 Analytische Geometrie von Geraden und 3.1 Darstellungen von Geraden . . . . . 3.2 Darstellungen von Ebenen . . . . . . 3.3 Weitere Bemerkungen und Hinweise 4 Reelle Vektorraume und Unterraume ¨ ¨ 4.1 Die Vektorraum-Definition . . . . . . . . . . . . . 4.2 Der Vektorraum Rn . . . . . . . . . . . . . . . . 4.3 Weitere Beispiele von reellen Vektorraumen . . . ¨ 4.4 Untervektorraume . . . . . . . . . . . . . . . . . ¨ 4.5 Der Nullraum einer Matrix . . . . . . . . . . . . 4.6 Linearkombinationen . . . . . . . . . . . . . . . . 4.7 Die vier Fundamentalraume einer Matrix . . . . ¨ 4.8 Der Spaltenraum und lineare Gleichungssysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 . 87 . 90 . 91 . 92 . 94 . 96 . 100 . 101 8 Inhaltsverzeichnis 4.9 4.10 4.11 4.12 4.13 4.14 4.15 4.16 4.17 4.18 4.19 Lineare Unabhangigkeit . . . . . . . . . . . . . . ¨ Basis und Dimension . . . . . . . . . . . . . . . . Die Struktur der Losungsmenge von Ax = b . . ¨ Basen des Zeilen-, Spalten- und Nullraumes einer Die Dimensionen der vier Fundamentalraume . . ¨ Der Euklidische Vektorraum Rn . . . . . . . . . . Die Orthogonalitat . ¨ der vier Fundamentalraume ¨ Orthogonale Projektionen . . . . . . . . . . . . . Lineare Ausgleichsrechnung . . . . . . . . . . . . Orthogonal- und Orthonormalbasen . . . . . . . Weitere Bemerkungen und Hinweise . . . . . . . 5 Determinanten 5.1 Die Determinante einer (2, 2)-Matrix . 5.2 Verallgemeinerung auf (n, n)-Matrizen 5.3 Determinanten und lineare Systeme . 5.4 Weitere Bemerkungen und Hinweise . . . . . . . . . . . . . . . . Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103 105 108 111 115 117 119 121 128 132 138 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144 144 146 149 154 6 Eigenwerte und Eigenvektoren 6.1 Wie berechnet man Eigenwerte und Eigenvektoren? 6.2 Diagonalisierung einer Matrix . . . . . . . . . . . . . 6.3 Orthogonale Matrizen . . . . . . . . . . . . . . . . . 6.4 Diagonalisierung mit orthogonalen Matrizen . . . . . 6.5 Weitere Bemerkungen und Hinweise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156 158 163 168 172 176 . . . . . . . . . . . . . . . . . . . . . . . . 7 Lineare Abbildungen und Matrizen 178 7.1 Lineare Abbildungen von Rn nach Rm . . . . . . . . . . . . . 178 7.2 Beispiele linearer Abbildungen . . . . . . . . . . . . . . . . . 183 7.3 Weitere Bemerkungen und Hinweise . . . . . . . . . . . . . . 185 Losungen ¨ 187 Literaturverzeichnis 195 Sachwortverzeichnis 196 1 Lineare Gleichungssysteme und Matrizen The simplest model in applied mathematics is a system of linear equations. It is also by far the most important. Gilbert Strang In vielen realen, aber auch innermathematischen Problemen treten lineare Gleichungssysteme auf; ihre Behandlung ist eines der wichtigsten Themen der Linearen Algebra. In der Elektrotechnik etwa fuhrt die Anwendung ¨ der Kirchhoffschen Knotenregel fur Schaltkreise auf lineare Gleichungs¨ ¨ systeme, Bilanzaufgaben in Technik und Okonomie werden mit linearen Systemen modelliert. Innerhalb der Mathematik werden Losungen nichtlinea¨ rer Gleichungssysteme und Optimierungsaufgaben mit linearen Systemen gesucht (Quasi-Newton-Verfahren). Interpolationen und Approximationen von Kurven und Flachen mittels Spline- und anderer Funktionen fuhren ¨ ¨ auf lineare Systeme. Die Integration von Anfangswertaufgaben bei Systemen gewohnlicher Differenzialgleichungen, die Diskretisierung von Randwertauf¨ gaben bei gewohnlichen und partiellen Differenzialgleichungen mittels Dif¨ ferenzenverfahren oder finiter Elemente oder das Losen von Anfangs- und ¨ Randwertaufgaben bei partiellen Differenzialgleichungen fuhrt uber lineare ¨ ¨ Gleichungssysteme zur Losung. ¨ Zur sachgerechten Behandlung mathematischer Probleme der Technik und Wirtschaft, etwa zu Netzwerkberechnungen in der Elektrotechnik oder zur Berechnung von Fachwerken in der Statik, zur Losung von Transportproble¨ men oder anderen Optimierungsaufgaben, zur qualitativen und quantitativen Diskussion mechanischer dynamischer Systeme bedient man sich der Matrizenrechnung. 1.1 Lineare Gleichungssysteme Die Gleichung 2x − 5 = 3 ist eine lineare Gleichung, weil die Variable x linear in ihr vorkommt. Lost ¨ man die Gleichung 2x − 5 = 3 nach der Unbekannten x auf, so erhalt ¨ man die Losung x = 4. ¨ p 10 1 Lineare Gleichungssysteme und Matrizen Allgemein ist eine lineare Gleichung in einer Variablen x von der Form ax = b, wobei a, b reelle Konstanten sind. Fur 0 ist x = b/a die Losung. Eine ¨ a = ¨ lineare Gleichung in n Variablen x1 , x2 , . . . , xn hat die Gestalt a1 x1 + a2 x2 + · · · + an xn = b, wobei a1 , a2 , . . . , an und b gegebene reelle Konstanten sind. Die reellen Zahlen ai nennt man die Koeffizienten der Gleichung und b ∈ R ist die rechte Seite der Gleichung (Zur Schreibweise sei bemerkt, dass wir fur ¨ die Variablen x1 , x2 , x3 einer Gleichung auch x, y oder z schreiben. Kommen mehr als drei Unbekannte vor, so schreiben wir x mit Index, also x1 , x2 usw.). Eine Losung der linearen Gleichung a1 x1 + a2 x2 + · · · + an xn = b ist eine ¨ endliche Folge (n-Tupel) von n Zahlen x̄1 , x̄2 , . . ., x̄n mit der Eigenschaft, dass die Gleichung durch die Substitution x1 = x̄1 , x2 = x̄2 , . . ., xn = x̄n erfullt heißt allgemeine Losung ¨ wird. Die Gesamtheit aller Losungen ¨ ¨ (Losungsmenge) der Gleichung. ¨ Beispiel 1.1 Finden Sie die allgemeine Losung der Gleichung ¨ 4x − 2y = 1. Losung: Um Losungen dieser Gleichung zu finden, konnen wir fur ¨ ¨ ¨ ¨ x einen beliebigen Wert aus R wahlen und nach y auflosen; alternativ konnen wir ¨ ¨ ¨ auch irgendeinen Wert fur und nach x auflosen. Der erste Ansatz ¨ y wahlen ¨ ¨ liefert fur ¨ x = t, wobei t ∈ R beliebig ist, y = 2t − 1/2. Die derart bestimmte parameterabhangige Losung ¨ ¨ x = t, y = 2t − 1/2 ist die allgemeine Losung, jede spezielle Wahl des Parameters t ergibt ¨ eine spezielle Losung (Teillosung). Einzelne Losungen erhalten wir durch ¨ ¨ ¨ Einsetzen entsprechender Zahlen fur t. Beispielsweise liefert t = 3 die Losung ¨ ¨ x = 3, y = 11/2. Schlagen wir die zweite Losungsstrategie ein, so erhalten ¨ wir x = 1/2t + 1/4, y = t. Obwohl sich diese Formeln von den ersten unterscheiden, beschreiben sie dieselbe allgemeine Losung. Zum Beispiel liefert hier t = 11/2 genau die ¨ Losung x = 3, y = 11/2, die wir oben fur ¨ ¨ t = 3 erhalten haben. 1.1 Lineare Gleichungssysteme 11 ¨ Ublicherweise treten lineare Gleichungen mit mehreren Variablen nicht einzeln auf. Kommen endlich viele Gleichungen mit den Variablen x1 , x2 , . . ., xn vor, so spricht man von einem linearen Gleichungssystem. Die m linearen Gleichungen a11 x1 + a12 x2 + · · · + a1n xn = b1 a21 x1 + a22 x2 + · · · + a2n xn = .. . b2 am1 x1 + am2 x2 + · · · + amn xn = bm ergeben ein lineares Gleichungssystem mit n Variablen. Die beiden Gleichungen x1 − 2x2 = 1 3x1 + 2x2 = 11 bilden ein lineares Gleichungssystem mit zwei Unbekannten, das heißt, es ist m = 2 und n = 2. Eine Losung des linearen Gleichungssystems ist eine endliche Folge von ¨ n Zahlen (n-Tupel) x̄1 , x̄2 , . . ., x̄n mit der Eigenschaft, dass jede Gleichung erfullt ¨ ist, wenn man x1 = x̄1 , x2 = x̄2 , . . ., xn = x̄n in das Gleichungssystem einsetzt. Besitzt ein lineares System keine Losung, so sagt ¨ man, es ist unlosbar (inkonsistent); hat es eine Losung, so ist es losbar ¨ ¨ ¨ (konsistent). Sind die rechten Seiten des Gleichungssystems Null, das heißt b1 = b2 = · · · = bm = 0, so heißt das System homogen. Beachten Sie, dass ein homogenes Gleichungssystem stets die Losung x1 = x2 = · · · = xn = 0 ¨ hat; man nennt sie die triviale Losung. ¨ Zwei Gleichungssysteme sind ¨ aquivalent, wenn sie dieselbe Losungsmenge ¨ haben. Das lineare System x1 − 3x2 = −7 2x1 + x2 = 7 hat die Losung x1 = 2 und x2 = 3. Das lineare System ¨ 8x1 − 3x2 = 7 3x1 − 2x2 = 0 10x1 − 2x2 = 14 hat ebenfalls die Losung x1 = 2 und x2 = 3. Daher sind die beiden Systeme ¨ ¨aquivalent. 12 1 Lineare Gleichungssysteme und Matrizen 1.2 Matrizen Das rechteckige Zahlenschema ⎡ a11 a12 · · · a1n ⎢ a21 a22 · · · a2n ⎢ ⎢ .. .. .. .. ⎢ . . . . ⎢ ⎢ ai1 ai2 · · · ain ⎢ ⎢ . .. .. .. ⎣ .. . . . am1 am2 · · · amn ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ mit aij ∈ R, i = 1, 2, . . . , m, j = 1, 2, . . . , n heißt Matrix mit m Zeilen und n Spalten oder (m, n)-Matrix. Die reellen Zahlen aij sind die Elemente der Matrix. Zum Beispiel ist √ 1 2 −2 7 −3 π eine Matrix mit 2 Zeilen, 3 Spalten und insgesamt 6 Elementen. Ein lineares Gleichungssystem mit m Gleichungen und n Unbekannten konnen wir als ¨ Matrix in der Form ⎡ ⎤ a11 a12 · · · a1n b1 ⎢ a21 a22 · · · a2n b2 ⎥ ⎢ ⎥ ⎢ .. .. .. .. .. ⎥ ⎢ . ⎥ . . . . ⎢ ⎥ ⎢ ai1 ai2 · · · ain bi ⎥ ⎢ ⎥ ⎢ . .. .. .. .. ⎥ ⎣ .. . . . . ⎦ am1 am2 · · · amn bm schreiben, wenn wir uns merken, dass die Matrixelemente in der j-ten Spalte mit der Variablen xj zu multiplizieren sind, zwischen zwei Spalten ein Pluszeichen + und zwischen der vorletzten und letzten Spalte ein Gleichheitszeichen = steht. Wir nennen diese Matrix die erweiterte Koeffizientenmatrix des linearen Gleichungssystems. Erweitert deshalb, weil die rechte Seite des Gleichungssystems mit in die Matrix aufgenommen wird. Ist dies nicht der Fall, so spricht man nur von der Koeffizientenmatrix des linearen Systems. Zum Beispiel hat das lineare Gleichungssystem x1 + x2 + 2x3 = 9 2x1 + 4x2 − 3x3 = 1 3x1 + 6x2 − 5x3 = 0 1.3 Elementare Umformungen und Zeilenstufenformen 13 die erweiterte Koeffizientenmatrix ⎤ ⎡ 1 1 2 9 ⎣ 2 4 −3 1 ⎦ . 3 6 −5 0 Mit Hilfe von Matrizen konnen wir lineare Gleichungssysteme ubersichtlicher ¨ ¨ und kompakter schreiben und behandeln. 1.3 Elementare Umformungen und Zeilenstufenformen Wir entwickeln nun ein Losungsverfahren fur ¨ ¨ lineare Gleichungssysteme. Die grundlegende Idee dieses Verfahrens besteht darin, das gegebene System in ein aquivalentes System zu bringen, das einfacher gelost ¨ ¨ werden kann. Systeme, die einfach zu losen sind, sind zum Beispiel Systeme in Diagonalform“, ¨ ” Dreiecksform“ oder Orthogonalform“. Wir betrachten folgende drei grund” ” legende Operationen. Elementare Gleichungsumformungen: • Vertauschen von zwei Gleichungen, • Multiplikation einer Gleichung mit einer von Null verschiedenen Konstanten, • Addition eines Vielfachen einer Gleichung zu einer anderen Gleichung. Unter einer elementaren Gleichungsumformung versteht man solch eine Operation. Satz 1.1 Elementare Gleichungsumformungen andern nicht die Losungsmenge eines ¨ ¨ linearen Gleichungssystems. Anders ausgedruckt: Lineare Systeme, die durch elementare Gleichungsum¨ formungen auseinander hervorgehen, sind ¨aquivalent; sie haben die gleiche Losungsmenge. Da die Zeilen der erweiterten Koeffizientenmatrix den Glei¨ chungen des zugehorigen Systems entsprechen, liefern die elementaren Glei¨ chungsumformungen folgende elementare Zeilenumformungen innerhalb der erweiterten Koeffizientenmatrix. Sachwortverzeichnis Alle fett gedruckten Seitenzahlen sind Referenzen auf die Definition des jeweiligen Begriffs. Demgegenüber geben normal gedruckte Seitenzahlen die Seiten der Verwendung des jeweiligen Begriffs wieder. Abbildung affin-lineare, 180 identische, 183 lineare, 178, 179 Abgeschlossenheit gegenüber der skalaren Multiplikation, 92 gegenüber der Vektoraddition, 92 Addition von Vektoren, 50, 53 äquivalente Gleichungssysteme, 11 affin-lineare Abbildung, 180 allgemeine Lösung eines Gleichungssystems, 10 Approximation, 9 Ausgleichsproblem lineares, 128 Basis, 105, 105, 132, 134, 151, 161, 163, 170, 173, 174, 181, 193, 194 orthogonale, 133 orthonormale, 133 Betrag eines Vektors, 59 Bildraum, 138 Blockmatrix, 29 charakteristische Gleichung, 158 charakteristisches Polynom, 158 Cramersche Regel, 152 Darstellungsmatrix, 182 Determinante, 144–148, 151, 159, 176 einer (2, 2)-Matrix, 144 einer (3, 3)-Matrix, 146 diagonalisierbare Matrix, 164 Diagonalmatrix, 23, 24, 166, 172 Dimension, 108 Drehimpuls, 69 Drehmoment, 69, 73 Drehungen, 185 Dreiecksungleichung, 180 dyadisches Produkt, 32, 73 Ebenengleichung in Parameterform, 79 Eigenpaar, 156 Eigenraum, 161, 162, 168 Eigenvektor einer Matrix, 156 Eigenvektoren, 158–166, 172, 173, 176 Eigenvektorenmatrix, 163, 166, 167, 173, 174 Eigenwert, 157–162, 166 einer Matrix, 156 Eigenwertaufgabe, 160, 160, 176 Eigenwertmatrix, 166 Einheitsmatrix, 24, 169 Einheitsvektor, 59 elementare Gleichungsumformung, 13 elementare Zeilenumformung, 13, 111 Elemente der Matrix, 12 endlich dimensionaler Vektorraum, 108 endliche Folge, 10, 11 Erzeugendensystem, 100 Euklidische Länge, 119 Sachwortverzeichnis 197 Euklidische Norm, 119 Euklidischer Vektorraum, 117 Hauptdiagonale, 23 Hintereinanderausführung, 50, 50 führende Eins, 14, 14, 115 führende Variablen, 16, 115 Falksches Schema, 27 Fehlervektor, 126 Folge endliche, 10, 11 freie Variablen, 16, 115 Fundamentalräume, 101 Fundamentalsatz der Algebra, 158 Funktion lineare, 178 reelle, 178 Funktionalanalysis, 185 identische Abbildung, 183 inkonsistentes Gleichungssystem, 11 Interpolation, 9 Inverse, 38 Moore-Penrose, 129 inverse Matrix, 38 invertierbare Matrix, 38 Gauß-Jordan-Verfahren, 16 Gauß-Verfahren, 17 Gegenvektor, 49, 88 Geometrie, 48, 69, 73, 86, 156 geordnete Paare, 52 Geradengleichgung in Parameterform, 77 gleiche Vektoren, 49 Gleichung charakteristische, 158 lineare, 10 Gleichungssystem homogenes, 11 inhomogenes, 11 inkonsistentes, 11 konsistentes, 11 lösbares, 11 lineares, 11 unlösbares, 11 Gleichungssysteme äquivalente, 11 Gleichungsumformung elementare, 13 Gram-Schmidtsches Orthogonalisierungsverfahren, 137 Gram-Schmidtsches Orthonormalisierungsverfahren, 138 kartesisches Koordinatensystem, 52 kartesisches Produkt, 52 Kehrmatrix, 38 Kern, 138 Koeffizienten einer linearen Gleichung, 10 einer Linearkombination, 96 Koeffizientenmatrix, 12, 94, 111 eines linearen Systems, 12 erweiterte, 12 Komplement orthogonales, 120 komplexe Zahlen, 88 komplexer Vektorraum, 88 konsistent, 11 konsistentes Gleichungssystem, 11 Koordinaten, 53 Koordinatendarstellung, 81 der Ebene, 80 der Geraden, 76 Koordinatenebenen, 55 Koordinatengleichung, 78, 81, 82 Koordinatengleichung der Ebene, 80 Koordinatensystem kartesisches, 52 rechtwinkliges, 52 Koordinatentransformationen, 180 Koordinatenursprung, 98, 109 Kosinussatz, 62 Kraft nach Lorentz, 69 Kraftfeld, 73 Kreuzprodukt, 69, 69, 73 198 Sachwortverzeichnis Länge Euklidische, 118 eines Vektors, 118 lösbares Gleichungssystem, 11 Lösung eines linearen Gleichungssystems, 11 linearer Gleichungen, 10 Lösungsraum, 95 linear abhängig, 103 linear unabhängig, 103 lineare Abbildung, 178, 179 lineare Funktion, 178 lineare Gleichungen, 10 lineare Hülle, 97, 98, 123 lineare Transformation, 179, 183, 185 linearer Operator, 185 lineares Ausgleichsproblem, 128 lineares Gleichungssystem, 11, 37, 82, 96 Linearkombination von Matrizen, 27 von Vektoren, 96 Matlab, 74, 176 Matrix Diagonal-, 23 diagonalisierbare, 164 Einheits-, 24 inverse, 38 invertierbare, 38 Null-, 23 obere Dreiecks-, 24 orthogonale, 124, 168 quadratische, 23 reguläre, 38 symmetrische, 24, 124, 163, 173 transponierte, 23 untere Dreiecks-, 24 Matrixelemente, 12 Matrixprodukt skalares, 26 Matrizen gleiche, 24 ungleiche, 24 Matrizenaddition, 25 Matrizengleichung, 40, 42, 164 Matrizenprodukt, 42, 63 Matrizensubtraktion, 26 Menge von Vektoren, 132 orthogonale, 132 orthonormale, 132 Modalmatrix, 163 Multiplikation von Matrizen, 27 Multiplikation eines Skalars mit einem Vektor, 54 Multiplikation mit Skalaren, 51 Multipliklation skalare, 88 natürliche Basis, 106 negativer Vektor, 88 Norm Euklidische, 118 eines Vektors, 59, 118 Normalenform einer Ebenengleichung, 82 Normalenvektor, 83 Normalenvektor der Ebene, 82 Normalgleichungssystem, 126 normalisierter Vektor, 133 Normalsystem, 126 Nullabbildung, 183 Nullmatrix, 23, 34 Nullpunkt, 52 Nullraum, 95, 95, 96, 100, 101, 109, 111–114, 116, 117, 120, 126, 138, 151, 162 Nullunterraum, 95 Nullvektor, 49, 88 der Translationen, 49 der Verschiebungen, 49 Nullvektorraum, 93, 93 numerisch stabil, 171 obere Dreiecksmatrix, 24 Operator Sachwortverzeichnis linearer, 185 orthogonal, 65 Orthogonalbasis, 133, 135, 136 orthogonale Basis, 133 orthogonale Matrix, 124, 168 orthogonale Menge, 132 orthogonale Projektion, 66, 121, 128 orthogonale Projektionsmatrix, 124, 126 orthogonale Unterräume, 119 orthogonales Komplement, 120 Orthogonalprojektion, 66, 68 Orthonormalbasis, 133, 172, 173 orthonormale Basis, 133 orthonormale Menge, 132 orthonormale Vektoren, 119 Ortsvektor, 53 Parallelogramm, 50, 70 Parallelogrammregel, 50 parameterfreie Ebenengleichung, 83 Parametergleichung, 78, 80, 81 einer Ebene, 79 einer Geraden, 77 Pfeil eines Vektors, 48 Polynom charakteristisches, 158 Produkt, 54 dyadisches, 32, 73 kartesisches, 52 Skalar mit Vektor, 54 skalares Matrix-, 26 von Matrizen, 27 Produktmenge, 52 Projektion, 181 orthogonale, 66, 121 Projektionsmatrix orthogonale, 124, 126 Pseudoinverse, 129 Punkt-Normalenform einer Ebenengleichung, 82 199 quadratische Matrix der Ordnung n, 23 Rückwärtssubstitution, 17, 17, 19 Rang, 115, 116, 124 Raum reeller linearer, 87 Rechenregeln, 48 rechte Seite einer linearen Gleichung, 10 rechtwinkliges Koordinatensystem, 52 reduzierte Staffelform, 45 reduzierte Zeilenstufenform, 15, 22, 45 reelle Funktion, 178 reeller linearer Raum, 87 reeller Vektorraum, 87 reguläre Matrix, 38 Repräsentant eines Vektors, 48, 48 Residuenvektor, 126 Richtungsvektor, 77, 78, 188 Rotation, 181 Satz des Pythagoras im Rn , 119 Schema nach Falk, 27 Skalare, 23, 88 skalare Multiplikation, 51, 54, 55, 88 skalares Matrixprodukt, 26 skalares Produkt, 54 skalares Vektorprodukt, 61, 61 skalares Vielfaches, 51 Skalarmultiplikation, 88 Skalarprodukt, 61, 69, 73, 118, 171 Spaltenmatrix, 22 Spaltenraum, 99, 99, 100–103, 108, 112, 115–117, 120, 122–126, 128 spaltenweise Berechnung des Matrizenproduktes, 31 Spannvektoren, 79 Spektraldarstellung, 174, 174 Spektralsatz, 174 200 Sachwortverzeichnis Spiegelungen, 183 Stützvektor der Ebene, 79 Stützvektor der Geraden, 77 Staffelform, 45 reduzierte, 45 Standardbasis, 106 Standarddarstellungsmatrix, 182 Standardmatrix, 182, 184 Summe, 53 einer Matrix, 25 von Vektoren, 55 symmetrische Matrix, 24, 124, 163, 173 Transformation, 183 lineare, 179, 183, 185 Translationen, 48 transponierte Matrix, 23 triviale Lösung eines Gleichungssystems, 11 unlösbares Gleichungssystem, 11 untere Dreiecksmatrix, 24 Untermatrizen, 29 Unterräume orthogonale, 119 triviale, 93 Unterraum, 92, 93, 98, 99, 101, 109, 122, 124, 162, 174 aufgespannter, 100 erzeugter, 100 Untervektorraum, 92 Ursprung, 52 Variablen führende, 16 freie, 16 Vektor, 55 geometrischer, 48 in der Ebene, 52 in der Geometrie, 48 negativer, 88 normalisiert, 133 Vektoraddition, 50, 50, 53, 88 Vektoren, 48, 87 gleiche, 49 orthogonale, 65, 119 orthonormale, 119 senkrechte, 65, 119 Vektorgleichung, 78, 103, 158–160, 188 Vektorraum, 119, 156, 178 Euklidischer, 117 endlich dimensionaler, 108 reeller, 87 Vektorraumhomomorphismus, 185 verallgemeinerte Inverse, 129 Verfahren nach Gauß-Jordan, 16 nach Gauß, 17 Verschiebungen, 48 vier Fundamentalräume, 101 Winkel zwischen Vektoren, 60 Zahlen komplexe, 88 Zeilenmatrix, 22, 63 Zeilenraum, 99, 99, 100, 101, 111, 112, 114–117, 120 Zeilenstufenform, 14, 14, 15–22, 45, 46, 113 Zeilenumformung elementare, 13, 111 zeilenweise Berechnung des Matrizenproduktes, 31