Grundwissenskatalog der 06. Jahrgangsstufe G8

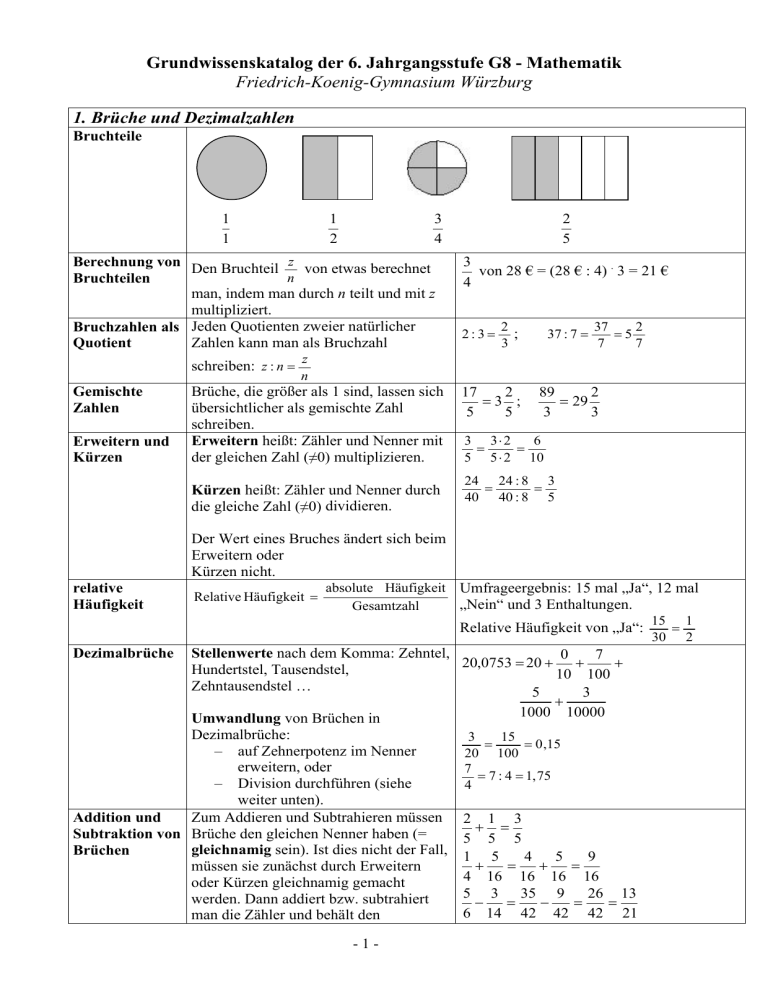
Grundwissenskatalog der 6. Jahrgangsstufe G8 - Mathematik
Friedrich-Koenig-Gymnasium Würzburg
1. Brüche und Dezimalzahlen
Bruchteile
1
1
1
2
3
4
Berechnung von Den Bruchteil z von etwas berechnet
n
Bruchteilen
man, indem man durch n teilt und mit z
multipliziert.
Bruchzahlen als Jeden Quotienten zweier natürlicher
Zahlen kann man als Bruchzahl
Quotient
schreiben: z : n =
Gemischte
Zahlen
Erweitern und
Kürzen
2
5
3
von 28 € = (28 € : 4) . 3 = 21 €
4
2:3=
2
;
3
37 : 7 =
37
2
=5
7
7
z
n
Brüche, die größer als 1 sind, lassen sich
übersichtlicher als gemischte Zahl
schreiben.
Erweitern heißt: Zähler und Nenner mit
der gleichen Zahl (≠0) multiplizieren.
Kürzen heißt: Zähler und Nenner durch
die gleiche Zahl (≠0) dividieren.
17
2
=3 ;
5
5
89
2
= 29
3
3
3 3⋅ 2
6
=
=
5 5 ⋅ 2 10
24 24 : 8 3
=
=
40 40 : 8 5
Der Wert eines Bruches ändert sich beim
Erweitern oder
Kürzen nicht.
relative
Häufigkeit
Relative Häufigkeit =
absolute Häufigkeit Umfrageergebnis: 15 mal „Ja“, 12 mal
„Nein“ und 3 Enthaltungen.
Gesamtzahl
15 1
Relative Häufigkeit von „Ja“:
=
30 2
Stellenwerte nach dem Komma: Zehntel,
0
7
20,0753 = 20 + +
+
Hundertstel, Tausendstel,
10 100
Zehntausendstel …
5
3
+
1000 10000
Umwandlung von Brüchen in
Dezimalbrüche:
3
15
=
= 0 ,15
– auf Zehnerpotenz im Nenner
20 100
erweitern, oder
7
= 7 : 4 = 1, 75
– Division durchführen (siehe
4
weiter unten).
Zum Addieren und Subtrahieren müssen 2 1 3
Addition und
+ =
Subtraktion von Brüche den gleichen Nenner haben (=
5 5 5
gleichnamig sein). Ist dies nicht der Fall, 1 5
Brüchen
4 5
9
+
=
+
=
müssen sie zunächst durch Erweitern
4 16 16 16 16
oder Kürzen gleichnamig gemacht
5 3 35 9 26 13
werden. Dann addiert bzw. subtrahiert
−
=
−
=
=
6 14 42 42 42 21
man die Zähler und behält den
Dezimalbrüche
-1-
gemeinsamen Nenner bei:
a b a+b
a b a−b
+ =
bzw. − =
c c
c
c c
c
Nach dem Gleichnamigmachen addiert
2 23 + 3 12 = 2 64 + 3 63 = 5 76 = 6 16
man die Ganzen und die Brüche.
Möglicherweise lässt sich aus dem Bruch
5
3
10
61 −2 =6 −2
=
noch ein Ganzes herausnehmen. Das
4
6
12
12
Subtrahieren erfolgt genauso.
15
10
5
=3
5 −2
Möglicherweise muss zuvor ein Ganzes
12
12
12
des Minuenden in einen Bruch
verwandelt werden.
Wie bei den natürlichen Zahlen wird
Addition und
13, 039
13, 447
Subtraktion von auch bei Dezimalbrüchen stellenweise
+ 7, 48
- 7, 48
Dezimalbrüchen addiert bzw. subtrahiert. Beim
20, 519
5, 967
Untereinanderschreiben muss man
deshalb Komma unter Komma
schreiben.
Addition und
Subtraktion von
gemischten
Zahlen
Multiplikation
von Brüchen
Multipliziere Nenner mit Nenner und
Zähler mit Zähler:
a c a⋅c
⋅ =
b d b⋅d
Vor dem Multiplizieren in Zähler und
Nenner ist soweit möglich zu kürzen.
b a⋅b
Sonderfall: a ⋅ =
c
c
2 3 2⋅3
6
=
⋅ =
7 5 7 ⋅ 5 35
5 18
5 ⋅ 18
1⋅3
3
⋅
=
=
=
12 25 12 ⋅ 25 2 ⋅ 5 10
9⋅
1
Division von
Brüchen
5 9 ⋅ 5 3 ⋅ 5 15
1
=
=
=7
=
6
6
2
2
2
3 2 7 2 7⋅2 1
⋅ = ⋅ =
=
4 7 4 7 4⋅7 2
Faktoren in gemischter Schreibweise sind
vor dem Multiplizieren in Brüche
umzuwandeln.
35 10 35 ⋅ 11 7 ⋅ 1 7
Multipliziere den Dividenden mit dem
:
=
=
=
Kehrbuch des Divisors.
44 11 44 ⋅ 10 4 ⋅ 2 8
Gemischte Zahlen müssen erst in Brüche
2
7
11 22 11 ⋅ 15 1 ⋅ 5
1
umgewandelt werden.
3 :1
:
=2
=
=
=
a
a
Sonderfall: : c =
(c ≠ 0)
b
b⋅c
Multiplikation Multipliziere zunächst ohne
Berücksichtigung der Kommas und setze
von
Dezimalbrüchen das Komma im Ergebnis so, dass es
ebenso viele Nachkommastellen wie die
beiden Faktoren zusammen besitzt.
-2-
3
15
3
15
3 ⋅ 22
1⋅2
6
6
2
:3 =
=
7
7⋅3 7
2, 1 · 6, 3 4
1 2 6
6 3
1
1 8 4
1 3, 3 1 4
0,23·0,4
92
0,092
2
Verschiebe das Komma bei beiden
Division von
Dezimalbrüchen Zahlen um gleich viele Stellen so weit
nach rechts, bis der Divisor eine
natürliche Zahl ist, und führe dann die
Division aus. Setze beim Überschreiten
des Kommas auch im Ergebnis ein
Komma.
Das Ergebnis einer Division kann auch
ein periodischer Dezimalbruch sein. Das
erkennst du, wenn sich beim
Divisionsverfahren ein Rest wiederholt.
3,78:1,4= 37,8:14 = 2,7
-28
98
-98
0
0,41:0,11= 41:11 = 3,72
-33
80
-77
30
-22
80
2. Flächeninhalte
Parallelogramm Ein Parallelogramm ist ein Viereck mit je
zwei parallelen Gegenseiten. Die Höhe h
steht senkrecht zur Grundlinie g und für
den Flächeninhalt A gilt:
A = g ⋅h
4cm
6cm
A = 4cm ⋅ 6cm
h
= ( 4 ⋅ 6)cm 2
g
Dreieck
= 24cm 2
Ein Dreieck ist ein halbes
Parallelogramm. Für seinen
Flächeninhalt A gilt:
1
A = ⋅ g ⋅h
2
4cm
6cm
A=
1
⋅ 4cm ⋅ 6cm
2
1
= ( ⋅ 4 ⋅ 6)cm 2
2
= 12cm 2
h
g
-3-
Trapez
3cm
c
a'
5cm
h
a
Vielecke
c'
7cm
Ein Trapez ist ein Viereck mit parallelen
1
Gegenseiten. Es lässt sich zu einem
A = ⋅ (3cm + 7cm ) ⋅ 5cm
2
Parallelogramm mit Grundlinie a+c und
Höhe h ergänzen. Für seinen
1
= ( ⋅ 10 ⋅ 5)cm 2
Flächeninhalt A gilt deshalb:
2
1
1
= 25cm 2
A = ⋅ AParallelogramm = ⋅ (a + c) ⋅ h
2
2
Den Flächeninhalt von Vielecken kann
man berechnen, indem man sie in die
oben genannten Grundformen zerlegt, die
einzelnen Flächeninhalte berechnet und
Dreieck 2
addiert..
Trapez
Dreieck 1
3. Volumen und Volumenmessung
Bedeutung
Einheiten
Das Volumen gibt an, welchen Raum ein Ein Würfel mit der Kantenlänge
Körper einnimmt.
1 cm hat das Volumen 1 cm3.
1 000 mm 3 = 1 cm 3
0,020 dm3 = 20 cm3 = 20 ml
1000 cm 3 = 1 dm 3
50 hl = 5000 l = 5000 dm3 = 5 m3
1000 dm 3 = 1 m 3
1l = 1 dm 3
1 ml = 1 cm 3
1000 ml = 1l
1 hl = 100 l
Volumen von
Quader und
Würfel
VQ = l ⋅ b ⋅ h („ Länge ⋅ Breite ⋅ Höhe “)
= G ⋅ h („Grundfläche · Höhe“)
VW = a ⋅ a ⋅ a = a 3
(„Kantenlänge hoch 3“)
Ein Würfel ist ein besonderer Quader.
Ein Quader ist 1,2 m lang, 38 cm
breit und 2,5 dm hoch. Für sein
Volumen gilt:
V Q = 12 dm ⋅ 3,8 dm ⋅ 2,5 dm =
= ( 12 ⋅ 3,8 ⋅ 2,5 ) dm 3
= 114 dm 3
-4-
4. Prozentrechnung
Festlegung
Prozent ist eine andere Schreib- und
Sprechweise für Hundertstel.
Grundgleichung Prozentwert = Prozentsatz · Grundwert
PW = PS · GW
25 1
= ;
100 4
120
1
=1
120% =
100
5
25% =
30%
von
PS
300 €
sind
90 €.
PW
GW
Von 40 Schülern sind 18 weiblich.
Das sind
1. 18
45
Berechnung des
PW
1. mit Formel PS =
Prozentsatzes
GW
2. mit Dreisatz
40
2.
=
100
= 45%
40 Schüler a 100%
100
%
40
100
18Schüler a 18 ⋅
% = 45%
40
1Schüler a
Berechnung des 1. mit Formel PW = PS ⋅ GW
Prozentwertes
2. mit Dreisatz
Von 40 Tomaten waren 35% faul.
Das sind
1. 35% ⋅ 40Tomaten =
35
⋅ 40Tomaten = 14Tomaten
100
2. 100% a 40Tomaten
40
Tomaten
100
40
Tomaten
35% a 35 ⋅
100
= 14Tomaten
1% a
Der Eintritt verteuerte sich um 15%,
so dass jetzt 4,60EUR zu bezahlen
sind. Früher kostete der Eintritt
1.
4,60
4,60
Berechnung des
PW
1. mit Formel GW =
Grundwertes
PS
2. mit Dreisatz
115%
=
2.
EUR =
115
100
EUR
460
EUR = 4,00 EUR
115
115% a 4,60 EUR
4,60
EUR
115
4,60
100% a 100 ⋅
EUR
115
= 4,00 EUR
1% a
-5-
5. Rationale Zahlen
Zahl und
Gegenzahl
Zahl und Gegenzahl sind auf der
Zahlengeraden gleich weit von der 0
entfernt.
Rationale
Zahlen
Bruchzahlen und ihre Gegenzahlen bilden − 2 ; 17 ; − 3; 5 2 sind
7
3
zusammen die rationalen Zahlen.
rationale Zahlen
Der Betrag |a| einer Zahl a ist ihr Abstand
3 3
=
|-3,8| = +3,8,
zur 0 auf der Zahlengeraden.
7 7
Betrag
Addition
Subtraktion
Multiplikation
7
7
und − 5
8
8
oder auch − 0, 41 und 0, 41 .
Gegenzahlen sind 5
Gleiche Vorzeichen:
Verschiedene
Vorzeichen:
(+ 1,2) + (+ 0,4) = +1,6
Subtrahiere den
(− 1,2) + (− 0,4) = −1,6
kleineren Betrag
vom größeren
Verschiedene Vorzeichen:
Betrag.
(− 1,2) + (+ 0,4) = −0,8
Gib der Differenz
das Vorzeichen des (+ 1,2) + (− 0,4 ) = +0,8
Summanden mit
dem größeren
Betrag.
Subtrahieren einer Zahl bedeutet dasselbe (− 1,2) − (− 0,4) = (− 1,2 ) + (+ 0,4)
wie Addieren ihrer Gegenzahl.
= −0,8
Gleiche
Vorzeichen:
Addiere die
Beträge.
Gib der Summe
das gemeinsame
Vorzeichen.
Multipliziere die Beträge.
Gib dem Ergebnis bei gleichen
Vorzeichen der Faktoren das
Vorzeichen +, bei verschiedenen
Vorzeichen der Vorzeichen das
Vorzeichen -.
(+ 0,5) ⋅ (+ 0,3) = +0,15 = 0,15
(− 0,5) ⋅ (− 0,3) = +0,15 = 0,15
(+ 0,5) ⋅ (− 0,3) = −0,15
(− 0,5) ⋅ (+ 0,3) = −0,15
Für alle rationalen Zahlen a gilt:
a ⋅ 0 = 0⋅ a = 0
a ⋅1 = 1 ⋅ a = a
Division
Dividieren durch eine Zahl bedeutet
dasselbe wie Multiplizieren mit ihrer
Kehrzahl.
Für alle rationalen Zahlen a ≠ 0 gilt:
0: a = 0.
Durch Null kann man nicht dividieren.
-6-
3  3 3  4
3⋅ 4
1
: −  = ⋅−  = −
=−
8  4 8  3
8⋅3
2
0 : (− 1,5) = 0
Verbindung der 1. Klammern haben absoluten Vorrang.
Grundrechenar- 2. Es gilt "Potenz vor Punkt vor Strich".
3. Ansonsten wird von links nach rechts
ten
gerechnet.
Die letzte auszuführende Rechnung legt
die Termart fest.
  1  2  2 
1 +  − 2  ⋅ 3  :  − 5 

  
 
  1   5 
= 1 +  −  ⋅  −  =
  3   2 
2
2  5
5
⋅  −  = − = −1
3
3  2
3
2,5 − 0,5 2 = 2,5 − 0,25 = 2,25
3 2 2 1 2
1
− − = − =−
5 5 5 5 5
5
  1  2  2 
Der Term 1 +  −  ⋅  :  − 
  2  3  5 
ist ein Quotient.
-7-