7 Basis und Dimension eines reellen Vektorraums

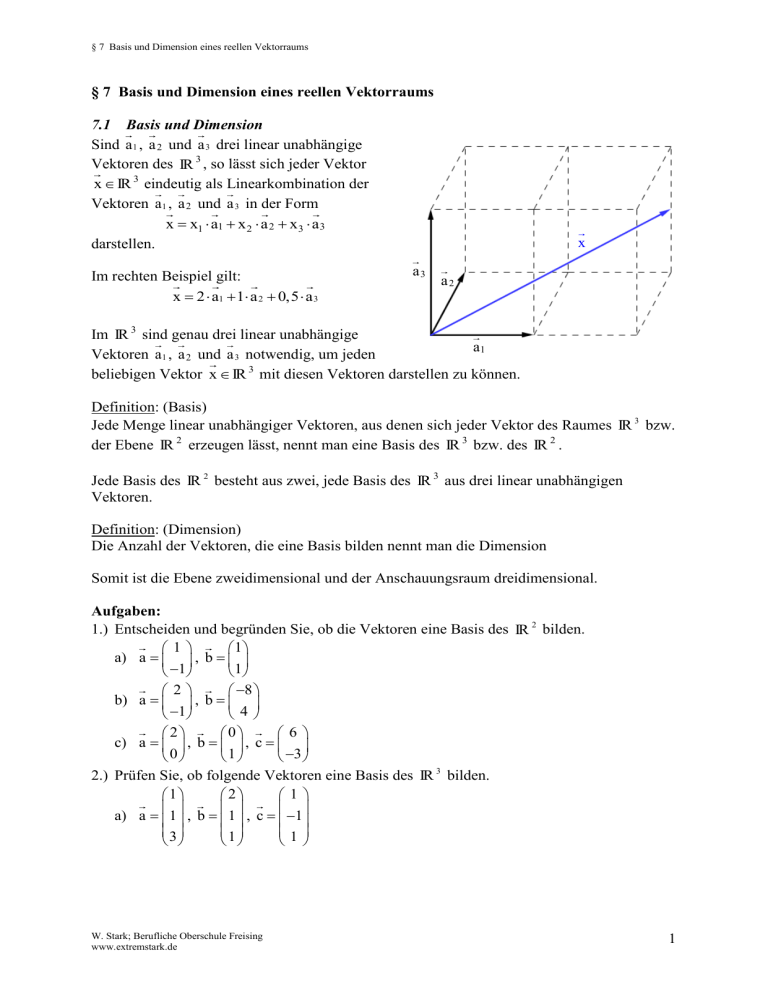
§ 7 Basis und Dimension eines reellen Vektorraums
§ 7 Basis und Dimension eines reellen Vektorraums
7.1 Basis und Dimension
Sind a1 , a 2 und a 3 drei linear unabhängige
Vektoren des IR 3 , so lässt sich jeder Vektor
x  IR 3 eindeutig als Linearkombination der
Vektoren a1 , a 2 und a 3 in der Form
x  x1  a1  x 2  a 2  x3  a 3
darstellen.
Im rechten Beispiel gilt:
x  2  a1  1 a 2  0,5  a 3
x
a3
a2
Im IR 3 sind genau drei linear unabhängige
a1
Vektoren a1 , a 2 und a 3 notwendig, um jeden
beliebigen Vektor x  IR 3 mit diesen Vektoren darstellen zu können.
Definition: (Basis)
Jede Menge linear unabhängiger Vektoren, aus denen sich jeder Vektor des Raumes IR 3 bzw.
der Ebene IR 2 erzeugen lässt, nennt man eine Basis des IR 3 bzw. des IR 2 .
Jede Basis des IR 2 besteht aus zwei, jede Basis des IR 3 aus drei linear unabhängigen
Vektoren.
Definition: (Dimension)
Die Anzahl der Vektoren, die eine Basis bilden nennt man die Dimension
Somit ist die Ebene zweidimensional und der Anschauungsraum dreidimensional.
Aufgaben:
1.) Entscheiden und begründen Sie, ob die Vektoren eine Basis des IR 2 bilden.
1
 1
a) a    , b   
 1
 1
2
 8 
b) a    , b   
 1
4
6
 2
0
c) a    , b    , c   
 3 
0
1
2.) Prüfen Sie, ob folgende Vektoren eine Basis des IR 3 bilden.
1
 2
1
 
 
 
a) a   1  , b   1  , c   1
1
 3
1
 
 
 
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
1
§ 7 Basis und Dimension eines reellen Vektorraums
 2
 1 
3
 
 
 
b) a   1  , b   4  , c   3 
6
 2 
5
 
 
 
1
 2
 1 
 
 
 
c) a   1  , b   1  , c   0 
 3
 2
 1 
 
 
 
3.) Bestimmen Sie k  IR so, dass die Vektoren a , b und c eine Basis des IR 3 bilden.
1
 2
k
 
 
 
a) a   0  , b   0  , c   1 
1
1
0
 
 
 
 2
1
4
 
 
 
b) a   1  , b   3  , c   1 
0
0
k
 
 
 
7.2 Koordinatendarstellung bezüglich einer Basis
Betrachtet man eine Basis B  b1 , b2 , b3 des IR 3 , so lässt sich jeder beliebiger Vektor


x  IR 3 eindeutig in der Form
x  x1  b1  x 2  b2  x 3  b3
mit reellen Zahlen x1, x 2 , x 3  IR darstellen.
Die reellen Zahlen x1 , x 2 und x 3 nennt man Koordinaten des Vektors x bezüglich der Basis
B.
1
 
Beispiel: Ermitteln Sie die Koordinaten des Vektors x   2  bezüglich der Basis B mit den
 3
 
1
1
1
 
 
 
Vektoren a   1  , b   0  und c  1 .
0
1
1
 
 
 
Der Ansatz
1
1
1
 1
 
 
 
 
 2   x1   1   x 2   0   x 3   1 
 3
0
1
 1
 
 
 
 
führt zu dem linearen Gleichungssystem
x1  x 2  x 3  1

x1
 x3  2
x 2  x3  3
x1  x 2
x2
x2
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
 x3
 x3
 1
 1
 3

x1  2
x 2  1
 x3  4
2
§ 7 Basis und Dimension eines reellen Vektorraums
Somit folgt: x  2  a  1 b  4  c
Bemerkung: Bezüglich unterschiedlicher Basen besitzt ein Vektor im Allgemeinen auch
unterschiedliche Koordinaten.
Aufgaben:
4.) Bestimmen Sie die Koordinaten der folgenden Vektoren bezüglich der Basis B mit den
 1
1
Vektoren a    und b    .
1
 3
 5 
a) x   
 7 
1
b) c   
0
5.) Bestimmen Sie die Koordinaten der folgenden Vektoren bezüglich der Basis B mit den
1
1
0
 
 
 
Vektoren a   1  , b   0  und c   1 
0
1
1
 
 
 
 3
 
a) d   1 
0
 
1
 
b) x   3 
 4 
 
7.3 Standardbasis
Eine besonders einfache (kanonische) Basis des IR 3 ist gegeben durch die Vektoren
1
0
0
 
 
 
e1   0  , e 2   1  und e3   0 
0
0
1
 
 
 
2
 
Die Koordinatendarstellung eines beliebigen Vektors a   1  IR 3 bezüglich dieser
3
 
Basisvektoren ist sehr einfach:
2
1
 0
 0
 
 
 
 
 1  2   0   1  1   3   0  bzw.
3
 0
 0
1
 
 
 
 
a  2e1  e2  3e3
Man bezeichnet die Basisvektoren e1 , e 2 und e3 auch als Standardbasis des IR 3 .
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
3
§ 7 Basis und Dimension eines reellen Vektorraums
Diese Vektoren bilden zusammen mit dem Punkt O (Ursprung) das uns schon bekannte
kartesische (benannt nach dem französischen Mathematiker René Descartes; 1596-1650)
Koordinatensystem. Diese Basisvektoren haben alle die Länge 1 und stehen paarweise
aufeinander senkrecht.
Aufgaben:
1
2
 1
 
 
 
6.) Zeigen Sie, dass die Vektoren c1   1 , c 2   1 und c3   1  eine Basis des IR 3
0
 1
2
 
 
 
2
 
bilden und geben Sie die Koordinaten des Vektors a   1 bezüglich dieser Basis an.
3
 
 3 
 
7.) Geben sie die Koordinaten des Vektors a   1  bezüglich der Standardbasis an.
4
 
 3
1
1
 
 
 
8.) Gegeben sind die Vektoren a   0  , b   1 und c  1
1
0
1
 
 
 
3
a) Zeigen Sie, dass diese Vektoren eine Basis des IR bilden.
b) Stellen Sie die Vektoren e1 , e 2 und e3 als Linearkombination der Vektoren
a , b und c dar.
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
4