Analysis für Informatiker - ReadingSample - Beck-Shop

eXamen.press
Analysis für Informatiker
Grundlagen, Methoden, Algorithmen
Bearbeitet von
Michael Oberguggenberger, Alexander Ostermann
1. Auflage 2005. Buch. XII, 326 S.
ISBN 978 3 540 21991 0
Format (B x L): 15,5 x 23,5 cm
Zu Inhaltsverzeichnis
schnell und portofrei erhältlich bei
Die Online-Fachbuchhandlung beck-shop.de ist spezialisiert auf Fachbücher, insbesondere Recht, Steuern und Wirtschaft.
Im Sortiment finden Sie alle Medien (Bücher, Zeitschriften, CDs, eBooks, etc.) aller Verlage. Ergänzt wird das Programm
durch Services wie Neuerscheinungsdienst oder Zusammenstellungen von Büchern zu Sonderpreisen. Der Shop führt mehr
als 8 Millionen Produkte.
1
Zahlen
Die aus dem Alltagsleben bekannten rationalen Zahlen (Bruchzahlen) reichen nicht
aus, um Analysis rigoros betreiben zu können. Die historische Entwicklung zeigt
vielmehr, dass für die Belange der Analysis der Zahlenbereich der rationalen Zahlen
zum Bereich der reellen Zahlen erweitert werden muss. Der Anschaulichkeit halber
führen wir die reellen Zahlen als Dezimalzahlen mit unendlich vielen Stellen ein.
Wir illustrieren exemplarisch, wie sich Rechenregeln und die Ordnungsrelation in
natürlicher Weise von den rationalen auf die reellen Zahlen übertragen.
Ein weiterer Abschnitt ist den Gleitpunktzahlen gewidmet, welche als praktikable
Approximation an die reellen Zahlen in den meisten Programmiersprachen implementiert sind. Insbesondere besprechen wir die optimale Rundung und die damit
zusammenhängende relative Maschinengenauigkeit.
1.1 Die reellen Zahlen
In diesem Buch setzen wir die folgenden Zahlensysteme als bekannt voraus:
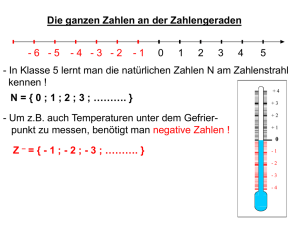
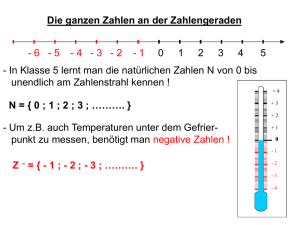
N = {1, 2, 3, 4, . . .}
die Menge der natürlichen Zahlen;
N0 = N ∪ {0}
die Menge der natürlichen Zahlen mit Null;
Z = {. . . , −3, −2, −1, 0, 1, 2, 3, . . .}
die Menge der ganzen Zahlen;
k
Q = n ; k ∈ Z und n ∈ N
die Menge der rationalen Zahlen.
sind genau dann gleich, wenn km = n gilt.
Zwei rationale Zahlen nk und m
Weiters identifiziert man eine ganze Zahl k ∈ Z mit der Bruchzahl k1 ∈ Q.
Offensichtlich gelten dann die Inklusionen N ⊂ Z ⊂ Q.
Seien M und N beliebige Mengen. Eine Abbildung von M nach N ist eine
Vorschrift, die jedem Element von M genau ein Element von N zuordnet1 .
1
In dieser Allgemeinheit werden wir den Begriff der Abbildung selten verwenden. Der für uns wichtige Spezialfall reellwertiger Funktionen wird im Kapitel 2
ausführlich besprochen werden.
2
1 Zahlen
Eine Abbildung heißt bijektiv, falls umgekehrt zu jedem Element n ∈ N genau
ein Element in M existiert, das n zugeordnet wird.
Definition 1.1 Zwei Mengen M und N werden gleich mächtig genannt,
wenn es eine bijektive Abbildung zwischen diesen Mengen gibt. Eine Menge M heißt abzählbar unendlich, wenn sie gleich mächtig wie N ist.
Die Mengen N, Z und Q sind gleich mächtig, in einem gewissen Sinn also gleich
groß. Alle drei Mengen haben unendlich viele Elemente, die abgezählt werden
können. Jede Abzählung stellt eine bijektive Abbildung zu N her. Die Abzählbarkeit von Z sieht man aus der Darstellung Z = {0, 1, −1, 2, −2, 3, −3, . . .}.
Für den Beweis der Abzählbarkeit von Q verwendet man das Diagonalverfahren nach Cantor2 :
3
1
2
4
1 → 1
1 → 1 ...
2
3
4
1
2
2
2
2 ...
↓ 2
3
4
1
3
3
3
3 ...
2
3
4
1
4
4
4
4 ...
..
..
..
..
.
.
.
.
Man zählt hier in Richtung der Pfeile ab, wobei jede rationale Zahl nur bei
ihrem ersten Auftreten berücksichtigt wird. Damit ist die Abzählbarkeit der
positiven rationalen Zahlen (und damit aller rationalen Zahlen) nachgewiesen.
Zur Veranschaulichung der rationalen Zahlen verwenden wir die Zahlengerade, welche man sich als (unendlich langes) Lineal vorstellen kann, bei dem
ein (beliebiger) Punkt als Null ausgezeichnet ist. Die ganzen Zahlen sind
äquidistant von Null ausgehend aufgetragen. Ebenso findet jede rationale
Zahl entsprechend ihrer Größe einen eindeutigen Platz auf der Zahlengeraden, vgl. Abb. 1.1.
−2
− 12
−1
0
1
3
1
2
1
a
2
Abb. 1.1. Die Zahlengerade.
Die Zahlengerade besitzt aber auch Punkte, die nicht rationalen Zahlen zuordenbar sind. (Man sagt, dass Q nicht vollständig ist.) Beispielsweise ist die
Länge der Diagonale d im Einheitsquadrat (vgl. Abb. 1.2) mit dem Lineal ab√
messbar. Bereits den Pythagoreern war bekannt, dass d2 = 2 gilt, aber d = 2
keine rationale Zahl ist.
2
G. Cantor, 1845–1918.
1.1 Die reellen Zahlen
Satz 1.2
√
2∈
/ Q.
√
3
2
1
Beweis: Der Beweis dieser
√ Aussage wird indirekt
2
wäre
rational.
Dann
geführt. Angenommen,
√
√
könnte man 2 als gekürzten Bruch 2 = nk ∈ Q
1
schreiben. Quadrieren ergibt k 2 = 2n2 und somit
Abb. 1.2. Diagonale
wäre k 2 eine gerade Zahl. Das ist nur möglich, wenn
im Einheitsquadrat.
k selbst gerade ist, also k = 2l. Dies oben eingesetzt
2
2
2
2
ergibt 4l = 2n und nach Kürzen 2l = n . Somit wäre n ebenfalls gerade,
was im Widerspruch zur Annahme steht, dass der Bruch nk gekürzt war. √
2
Bekanntlich ist 2 die eindeutige positive Nullstelle des Polynoms x − 2.
Die nahe liegende Vermutung, dass alle nicht rationalen Zahlen Nullstellen
von Polynomen mit ganzzahligen Koeffizienten sind, erweist sich jedoch als
falsch. Es gibt weitere nicht rationale Zahlen (die so genannten transzendenten
Zahlen), welche sich nicht so darstellen lassen. Beispielsweise ist die Kreiszahl
π = 3.141592653589793... ∈
/Q
transzendent, kann aber auf der Zahlengeraden dargestellt werden als der
halbe Umfang des Kreises mit Radius 1 (z.B. durch Abrollen).
Wir nehmen im Folgenden einen pragmatischen Standpunkt ein und konstruieren die fehlenden Zahlen als Dezimalzahlen.
Definition 1.3 Eine endliche Dezimalzahl x mit l Stellen hat die Form
x = ± d0 .d1 d2 d3 . . . dl
mit d0 ∈ N0 und den Ziffern di ∈ {0, 1, ..., 9}, 1 ≤ i ≤ l, wobei dl = 0 gilt.
Satz 1.4 (Darstellung rationaler Zahlen als Dezimalzahlen) Jede rationale
Zahl lässt sich als endliche oder periodische Dezimalzahl schreiben.
Beweis: Sei q ∈ Q, folglich q = nk mit k ∈ Z und n ∈ N. Man erhält die
Darstellung von q als Dezimalzahl durch sukzessive Division mit Rest. Da der
Rest r ∈ N jeweils die Bedingung 0 ≤ r < n erfüllt, wird der Rest spätestens
nach n Schritten Null oder periodisch.
Beispiel 1.5 Nehmen wir beispielsweise q = − 57 ∈ Q. Fortgesetzte Division
mit Rest zeigt, dass q = −0.71428571428571... mit Divisionsresten 5, 1, 3, 2,
6, 4, 5, 1, 3, 2, 6, 4, 5, 1, 3, . . . gilt. Die Periode dieser Dezimalzahl ist sechs.
Jede von Null verschiedene Dezimalzahl mit endlich vielen Stellen lässt sich
als periodische Dezimalzahl (mit unendlich vielen Stellen) schreiben. Dazu
vermindert man die letzte Dezimalstelle, die ja verschieden von Null ist, um
eins und ergänzt als weitere Dezimalen unendlich oft die Ziffer 9. Beispielsweise ist dann − 17
50 = −0.34 = −0.3399999... ab der dritten Stelle periodisch.
Damit kann Q als Menge jener Dezimalzahlen aufgefasst werden, deren Dezimalentwicklung ab einer bestimmten Stelle periodisch wird.
4
1 Zahlen
Definition 1.6 Als Menge der reellen Zahlen R bezeichnet man alle Dezimalzahlen der Form
± d0 .d1 d2 d3 ...
mit d0 ∈ N0 und den Ziffern di ∈ {0, ..., 9}, d.h. Dezimalzahlen mit unendlich
vielen Stellen. Die Menge R \ Q heißt Menge der irrationalen Zahlen.
Offensichtlich gilt Q ⊂ R. Nach dem bisher Gesagten sind die Zahlen
√
0.1010010001000010... und
2
irrational. Es gibt aber sehr viel mehr irrationale als rationale Zahlen, wie der
folgende Satz zeigt.
Satz 1.7 R kann nicht abgezählt werden, ist also mächtiger als Q.
Beweis: Der Beweis wird indirekt geführt. Wir nehmen an, man könnte die
reellen Zahlen zwischen 0 und 1 abzählen und schreiben eine Aufzählung an:
1
2
0. d11 d12 d13 d14 ...
0. d21 d22 d23 d24 ...
3
4
.
0. d31 d32 d33 d34 ...
0. d41 d42 d43 d44 ...
...
.
...
Mit Hilfe dieser Liste definieren wir nun die Dezimalstellen
1 falls dii = 2,
di =
2 sonst.
Dann ist x = 0.d1 d2 d3 d4 ... nicht in obiger Aufzählung enthalten im Widerspruch zur Annahme der Abzählbarkeit.
Obwohl R also bedeutend mehr Zahlen als Q enthält, lässt sich jede reelle Zahl
beliebig genau durch rationale Zahlen approximieren, z.B. π auf 9 Stellen
π≈
314159265
∈ Q.
100000000
Für praktische
√ Anwendungen genügen gute Approximationen an die reellen
Zahlen. Für 2 waren solche bereits den Babyloniern bekannt
√
2 ≈ 1; 24, 51, 10 = 1 +
51
24
10
+ 2 + 3 = 1.41421296... ,
60 60
60
vgl. Abb. 1.3. Die etwas ungewohnte Schreibweise kommt daher, dass die Babylonier in einem Zahlensystem zur Basis 60 rechneten.
1.2 Ordnungsrelation und Arithmetik auf R
5
30
1;24,51,10
5
42;25,3
Abb. 1.3. Babylonische Keilschrifttafel YBC 7289 (Yale Babylonian Collection, mit
Genehmigung) von 1900 vor unserer Zeit mit Übersetzung der Inschrift, nach [1].
Es ist ein Quadrat√mit Seitenlänge 30 und Diagonale 42; 25, 35 dargestellt. Das
Verhältnis beträgt 2 ≈ 1; 24, 51, 10.
1.2 Ordnungsrelation und Arithmetik auf R
Im Folgenden schreiben wir reelle Zahlen (eindeutig) als Dezimalzahlen mit
unendlich vielen Stellen, beispielsweise also 0.2999... statt 0.3.
Definition 1.8 (Ordnungsrelation) Seien a = a0 .a1 a2 ... und b = b0 .b1 b2 ...
nichtnegative reelle Zahlen in Dezimaldarstellung, d.h. a0 , b0 ∈ N0 .
(a) Man nennt a kleiner gleich b (und schreibt a ≤ b), falls a = b ist oder es
einen Index j ∈ N0 gibt mit aj < bj und ai = bi für i = 0, . . . , j − 1.
(b) Weiters legt man fest, dass −a ≤ b gilt und schreibt −a ≤ −b, falls b ≤ a.
Diese Definition setzt die bekannte Ordnung von N und Q auf R fort. Die
Ordnungsrelation ≤ besitzt folgende Interpretation auf der Zahlengeraden:
Es gilt a ≤ b, falls a auf der Zahlengeraden links von b liegt, wobei a = b
möglich ist.
Die Relation ≤ hat offenbar folgende Eigenschaften: Für alle a, b, c ∈ R gilt
a ≤ a (reflexiv),
a ≤ b und b ≤ c
⇒
a≤c
(transitiv),
a≤b
⇒
a=b
(antisymmetrisch).
und b ≤ a
Im Fall a ≤ b und a = b schreibt man a < b und nennt a kleiner b. Weiters
definiert man a ≥ b, falls b ≤ a ist (in Worten: a größer gleich b), und a > b,
falls b < a ist (in Worten: a größer b).
In ähnlicher Weise wie die Ordnung können Addition und Multiplikation von
Q auf R fortgesetzt werden. Anschaulich verwendet man, dass jeder reellen
Zahl eine Strecke auf der Zahlengeraden entspricht. Man definiert die Addition
reeller Zahlen dann als Addition der entsprechenden Strecken.
6
1 Zahlen
Eine rigorose und gleichzeitig algorithmische Definition der Addition geht
von der Beobachtung aus, dass reelle Zahlen beliebig genau durch rationale
Zahlen approximiert werden können. Seien a = a0 .a1 a2 ... und b = b0 .b1 b2 ...
zwei nichtnegative reelle Zahlen. Durch Abschneiden nach der k-ten Dezimale erhalten wir zwei rationale Approximationen a(k) = a0 .a1 a2 ...ak ≈ a
und b(k) = b0 .b1 b2 ...bk ≈ b. Dann ist a(k) + b(k) eine monoton wachsende
Approximation an die zu definierende Zahl a + b. Das erlaubt, a + b als Supremum dieser Approximationen zu definieren. Zur rigorosen Rechtfertigung
dieser Vorgangsweise verweisen wir auf Kap. 5. In gleicher Weise wird auch
die Multiplikation reeller Zahlen definiert. Es zeigt sich, dass die reellen Zahlen mit der Addition und der Multiplikation (R, +, ·) einen Körper bilden. Es
gelten somit die üblichen Rechenregeln, z.B. das Distributivgesetz
(a + b)c = ac + bc.
Der folgende Satz fasst einige wichtige Rechenregeln für ≤ zusammen. Die
Behauptungen können leicht mit Hilfe der Zahlengeraden verifiziert werden.
Satz 1.9 Für alle a, b, c ∈ R gilt
a≤b
a≤b
a≤b
⇒
a + c ≤ b + c,
und c ≥ 0
und c ≤ 0
⇒
⇒
ac ≤ bc,
ac ≥ bc.
Man beachte, dass a < b nicht a2 < b2 impliziert. Beispielsweise ist −2 < 1,
aber trotzdem gilt 4 > 1. Für a, b ≥ 0 gilt jedoch stets a < b ⇔ a2 < b2 .
Definition 1.10 (Intervalle) Die folgenden Teilmengen von R bezeichnet
man als Intervalle:
[a, b] = {x ∈ R ; a ≤ x ≤ b}
abgeschlossenes Intervall;
(a, b] = {x ∈ R ; a < x ≤ b}
[a, b) = {x ∈ R ; a ≤ x < b}
links halboffenes Intervall;
rechts halboffenes Intervall;
(a, b) = {x ∈ R ; a < x < b}
offenes Intervall.
Intervalle lassen sich, wie durch Abb. 1.4 illustriert wird, anschaulich auf der
Zahlengeraden darstellen.
a
b
c
d
e
f
Abb. 1.4. Die Intervalle (a, b), [c, d] und (e, f ] auf der Zahlengeraden.
Bemerkung 1.11 Es erweist sich als praktisch, die Symbole −∞ (minus
Unendlich) und ∞ (Unendlich) einzuführen, mittels der Eigenschaft
1.2 Ordnungsrelation und Arithmetik auf R
7
∀a ∈ R : −∞ < a < ∞.
Man definiert damit beispielsweise die uneigentlichen Intervalle
[a, ∞) = {x ∈ R ; x ≥ a}
(−∞, b) = {x ∈ R ; x < b}
und weiters (−∞, ∞) = R. Man beachte aber, dass −∞ und ∞ nur Symbole
und keine reellen Zahlen sind.
Als Anwendung der in Satz 1.9 gegebenen Eigenschaften der Ordnungsrelation
lösen wir exemplarisch einige Ungleichungen.
Beispiel 1.12 Man bestimme alle x ∈ R mit −3x − 2 ≤ 5 < −3x + 4.
In diesem Beispiel sind zwei Ungleichungen enthalten, nämlich
−3x − 2 ≤ 5
und
5 < −3x + 4.
Die erste Ungleichung wird umgeformt zu
−3x ≤ 7
⇔
7
x≥− .
3
Das ergibt eine erste Bedingung an x. Die zweite Ungleichung lautet
3x < −1
⇔
x<−
1
3
und ergibt eine zweite Bedingung an x. Die Lösung des ursprünglichen Problems muss beide Bedingungen erfüllen. Daher lautet die Lösungsmenge
1
7
7 1
L= x∈R; − ≤x<−
= − ,−
.
3
3
3 3
Beispiel 1.13 Man bestimme alle x ∈ R mit x2 − 2x ≥ 3.
Durch quadratisches Ergänzen formt man die Ungleichung um zu
(x − 1)2 = x2 − 2x + 1 ≥ 4.
Durch Wurzelziehen ergeben sich die zwei Fälle
x−1≥2
oder
x − 1 ≤ −2.
Die Vereinigung beider Fälle ergibt die Lösungsmenge
L = {x ∈ R ; x ≥ 3 oder x ≤ −1} = (−∞, −1] ∪ [3, ∞).
8
1 Zahlen
1.3 Maschinenzahlen
Die reellen Zahlen können nur unvollständig am Computer realisiert werden.
In exakter Arithmetik wie beispielsweise
√ in maple sind reelle Zahlen durch
symbolische Ausdrücke gegeben, z.B. 2 = RootOf( Z^2-2). Mit Hilfe des
Befehls evalf können diese auf sehr viele Stellen genau ausgewertet werden.
Die in Programmiersprachen üblicherweise als Modell für die reellen Zahlen
verwendeten Gleitpunktzahlen (floating point numbers) haben feste relative
Genauigkeit, z.B. double precision mit 52 Bit Mantissenlänge. Für diese Maschinenzahlen gelten die Rechenregeln von R nicht, z.B. ist
1 + 10−20 = 1
in double precision. Gleitpunktzahlen sind normiert durch das Institute of
Electrical and Electronics Engineers IEEE 754-1985 sowie durch die International Electrotechnical Commission IEC 559:1989. Im Folgenden geben wir
einen kurzen Abriss dieser Maschinenzahlen. Weiter gehende Informationen
findet man in [20, 27].
Man unterscheidet zwischen einfach langem und doppelt langem Format. Das
einfach lange Format (einfache Genauigkeit, single precision) benötigt 32 Bit
Speicherplatz
V
e
1
8
M
23
Das doppelt lange Format (doppelte Genauigkeit, double precision) benötigt
64 Bit Speicherplatz
V
e
1
11
M
52
Hier bezeichnet V ∈ {0, 1} das Vorzeichen, emin ≤ e ≤ emax ist der Exponent
(eine ganze Zahl mit Vorzeichen); schließlich ist M die Mantisse der Länge p
M = d1 2−1 + d2 2−2 + . . . + dp 2−p ∼
= d1 d2 . . . dp ,
dj ∈ {0, 1}.
Diese Darstellung entspricht der folgenden Zahl x:
x = (−1)V 2e
p
dj 2−j .
j=1
Normalisierte Gleitpunktzahlen in der Basis 2 haben stets d1 = 1. Deshalb
muss man d1 nicht speichern und enthält für die Mantissenlängen
einfach genau
doppelt genau
p = 24 ;
p = 53 .
1.4 Rundung
9
Der Einfachheit halber betrachten wir nur normalisierte Gleitpunktzahlen.
Mit M = Mmax und e = emax erhält man die größte Gleitpunktzahl
xmax = 1 − 2−p 2emax .
Mit M = Mmin und e = emin ergibt sich die kleinste positive (normalisierte)
Gleitpunktzahl
xmin = 2emin −1 .
Die Gleitpunktzahlen liegen nicht gleichmäßig auf der Zahlengeraden verteilt,
ihre relative Dichte ist aber annähernd konstant, vgl. Abb. 1.5.
2emin
2emin −1
0
2emin +1
Abb. 1.5. Gleitpunktzahlen auf der Zahlengerade, nach [27].
Im IEEE Standard gelten näherungsweise folgende Werte:
xmax
xmin
−38
einfach genau
1.18 · 10
3.40 · 1038
doppelt genau
2.23 · 10−308
1.80 · 10308
Weiters gibt es noch spezielle Symbole wie z.B.
±INF
...
±∞
NaN
...
not a number; z.B. bei Null dividiert durch Null.
Mit diesen Symbolen kann auch ohne Programmabbruch weitergerechnet werden.
1.4 Rundung
Sei x = a·2e ∈ R mit 1/2 ≤ a < 1 und xmin ≤ x ≤ xmax . Weiters bezeichne u, v
zwei Gleitpunktzahlen, welche x einschließen, d.h. u und v seien benachbarte
Maschinenzahlen mit u ≤ x ≤ v. Dann ist
u= 0
e
b1 . . . bp
und
v =u+ 0
e
00 . . . 01 = u + 0
e − (p − 1)
10 . . . 00
10
1 Zahlen
Somit gilt v − u = 2e−p . Für die optimale Rundung rd(x) von x ist daher
|rd(x) − x| ≤
1
(v − u) = 2e−p−1 .
2
Damit lässt sich der relative Fehler der Rundung angeben. Wegen
1
a
≤ 2 gilt
2e−p−1
|rd(x) − x|
≤
≤ 2 · 2−p−1 = 2−p .
x
a · 2e
Dieselben Überlegungen gelten für negative x (indem man den Betrag nimmt).
Definition 1.14 Die Zahl eps = 2−p heißt relative Maschinengenauigkeit.
Eine wichtige Anwendung dieses Konzepts ist der folgende Satz.
Satz 1.15 Sei x ∈ R mit xmin ≤ |x| ≤ xmax . Dann existiert ε ∈ R mit
rd(x) = x(1 + ε) und |ε| ≤ eps.
Beweis: Wir definieren
rd(x) − x
.
x
Nach der obigen Rechnung gilt |ε| ≤ eps.
ε=
Experiment 1.16 (Experimentelle Bestimmung von eps)
Sei z die kleinste positive Maschinenzahl, für die 1 + z > 1 gilt.
1= 0
1
100 . . . 00
,
z= 0
1
000 . . . 01 = 2 · 2−p .
Somit folgt z = 2 eps. Die Zahl z lässt sich experimentell bestimmen, und damit
auch eps. (Man beachte, dass in MATLAB die Zahl z als eps bezeichnet wird.)
Im IEC/IEEE Standard gilt:
einfach genau :
eps = 2−24 ≈ 5.96 · 10−8 ,
doppelt genau :
eps = 2−53 ≈ 1.11 · 10−16 .
Bei doppelt genauer Arithmetik hat man in etwa 16 Stellen Genauigkeit zur
Verfügung.
1.5 Übungen
1. Zeigen Sie, dass
√
3 irrational ist.
2. Beweisen Sie für alle a, b ∈ R die Dreiecksungleichung
|a + b| ≤ |a| + |b|.
1.5 Übungen
11
Hinweis: Unterscheiden Sie die Fälle, dass a und b entweder dasselbe oder verschiedenes Vorzeichen haben.
3. Lösen Sie die folgenden Ungleichungen sowohl händisch als auch mit maple (mittels solve). Geben Sie die Lösungsmenge in Intervallschreibweise an.
(a)
4x2 ≤ 8x + 1,
(c)
2 − x2 ≥ x2 ,
(e)
x2 < 6 + x,
1
> 3 + x,
3−x
1+x
(d)
> 1,
1−x
(f) |x| − x
≥ 1,
(g)
|1 − x2 | ≤ 2x + 2,
(h)
(b)
4x2 − 13x + 4 < 1.
4. Berechnen Sie die Binärdarstellung der Gleitpunktzahl x = 0.1 in einfach genauer
IEEE-Arithmetik (32 Bit Speicherplatz).
5. Bestimmen Sie experimentell die relative Maschinengenauigkeit eps.
Hinweis: Schreiben Sie in der Programmiersprache Ihrer Wahl ein Computerprogramm, das Ihnen die kleinste Maschinenzahl z mit 1 + z > 1 berechnet.