Ziel Rausausder Verlustzone! Grobziele Gewinne machen!
Werbung

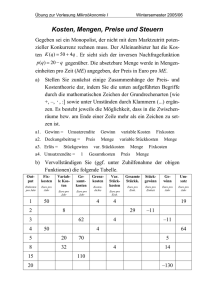
11.4.1 Break-even-Point-Analyse (Gewinnschwellenanalyse) 3 Wann schreibt ein Unternehmen „schwarze Zahlen“? Erstellen Sie eine kleine Formelsammlung, die Sie im Folgenden zur Durchführung der Break-even-Point-Analyse benötigen werden. Der Unternehmer eines kleinen Einproduktunternehmens möchte wissen, ab welcher Ausbringungsmenge das Unternehmen beginnt, „schwarze Zahlen“ zu schreiben. 1 Wie können Unternehmen die Grobziele, z.B.: „Wir müssen raus aus der Verlustzone!“ oder „Wir müssen endlich Gewinne machen!“ erreichen? Grobziele Rausausder Verlustzone! Ziel 4 Gewinne machen! 2 Der Break-even-Point (Deckungspunkt, Gewinnschwelle, Nutzenschwelle) bezeichnet den Schnittpunkt von Umsatz- und Kostenfunktion. Rechnerisch wird der Break-even-Point durch folgend Gleichungen ermittelt: [1] [2] [3] [4] U K p x xkrit KV kV KF db Umsatz U p·x p·x = = = = = = = = = = = = = Umsatz Kosten Fixe Kosten Variable Kosten Gewinn Break-even-Menge Break-even-Umsatz Kosten K KF + KV KF + kV·x Umsatz Kosten Stückpreis, Nettoverkaufspreis Stückzahl, Menge Produktionsmenge am Break-even-Point Variable Gesamtkosten (proportionale) variable Stückkosten Fixe Gesamtkosten Stückdeckungsbeitrag U= K= KF = KV = G= xkrit = Ukrit = Vervollständigen Sie die auf der folgenden Seite abgebildete Wertetabelle unter Berücksichtigung folgender Daten: Menge: Kapazitätsgrenze: Stückpreis: Variable Stückkosten: Fixe Kosten: 0 bis 800 ME/Periode (Schrittweite 100 ME) 800 ME/Periode 60,00 €/ME 20,00 €/ME 20.000,00 Euro/Periode 5 Bei welcher Produktionsmenge (xkrit) würde der Betrieb alle Kosten decken und die Gewinnschwelle erreichen? 6 Zeichnen Sie die Umsatzfunktion U und die Kostenfunktion K in ein Koordinatensystem (Gesamtkostendiagramm) und bestimmen Sie grafisch den Break-even-Point (Break-even-Menge, Break-even-Umsatz)! 7 Schraffieren Sie die Verlustzone und die Gewinnzone! Verwenden Sie möglichst die Farben rot und schwarz. 8 Zeichnen Sie in das Koordinatensystem auch die Gewinnfunktion G ein. 9 Erstellen Sie anhand der obigen Ausgangsdaten eine Wertetabelle für Lösen Sie die Gleichung [4] nach der Stückzahl (Menge) x auf. Wie lautet folglich die Formel zur Berechnung der kritischen Menge xkrit? die gesamten Stückkosten k, die fixen Stückkosten kF, die variablen Stückkosten kV, den Preis pro Stück, den Gewinn pro Stück, die Grenzkosten K’ = den Grenzumsatz U’ = dK dx Kritische Menge xkrit = (= erste Ableitung der Kostenfunktion K), dU dx (= erste Ableitung der Umsatzfunktion U) und stellen Sie die Graphen in einem Stückkostendiagramm dar. 10 Helmut Preis Arbeitsblätter Ökonomie 157 Erstellen Sie ein Arbeitsblatt mit einem Tabellenkalkulationsprogramm (z.B. Microsoft Excel®), mit dem Sie die Break-even-Point-Analyse (Gewinnschwellenanalyse) durchführen können. Helmut Preis Arbeitsblätter Ökonomie 158 12 Beantworten Sie schriftlich folgende Fragen: (1) Wie wird der Break-even-Point errechnet? (2) Wozu wird die Break-even-Point-Analyse eingesetzt? (3) Welche Informationen sind für die Break-even-Point-Analyse erforderlich? Der Absatzpreis eines Produkts beträgt 100 EUR/Stück (p) und die variablen Kosten betragen 40 EUR/Stück (kV). Pro Periode fallen dem Profit-Center zuordenbare fixe Kosten in Höhe von 80.000 EUR (KF) an. Die Produktionskapazität liegt bei 10.000 Stück (x). 13 Wie hoch sind der Umsatz und die Gesamtkosten sowie das Betriebsergebnis (Gewinn oder Verlust), wenn die höchstmögliche Produktionsmenge verkauft werden kann. 14 Bei welcher Absatzmenge (Break-even-Point) werden die Gesamtkosten dieses Profit-Centers gedeckt? Menge Umsatz Fixe Kosten x 0 100 200 300 400 500 600 700 800 U KF Menge Stückkosten x k Variable Stückkosten kV Variable Kosten KV Preis pro Stück p Gewinn pro Stück g Kosten Gewinn K G Grenzkosten K’ Menge Umsatz Fixe Kosten x 0 100 200 300 400 500 600 700 800 U KF Variable Kosten KV Kosten Gewinn K G GrenzUmsatz U’ 0 100 200 300 400 500 600 700 800 Helmut Preis Arbeitsblätter Ökonomie 159 Helmut Preis Arbeitsblätter Ökonomie 160 Menge Stückkosten x 0 100 200 300 400 500 600 700 800 k Variable Stückkosten kV Preis pro Stück p Gewinn pro Stück g Grenzkosten K’ GrenzUmsatz U’ Stückpreis: €/ME Variable Stückkosten: €/ME Fixe Kosten: €/Periode Kapazitätsgrenze: ME/Periode Menge x Umsatz U Kosten K Gewinn E–K 0 100 200 300 400 500 600 700 800 Helmut Preis Arbeitsblätter Ökonomie 161 Break-even-Point: ME Break-even-Umsatz: €/Periode Helmut Preis Arbeitsblätter Ökonomie 162 Menge x Stückpreis p Umsatz U 0 100 200 300 400 500 600 700 800 Menge Fixe Kosten x KF Variable Stückkosten kV Variable Kosten Kosten KV K 0 100 200 300 400 500 600 700 800 Helmut Preis Arbeitsblätter Ökonomie 163 Helmut Preis Arbeitsblätter Ökonomie 164