Kosten Umsatz a) Ermitteln Sie rechnerisch und grafisch den

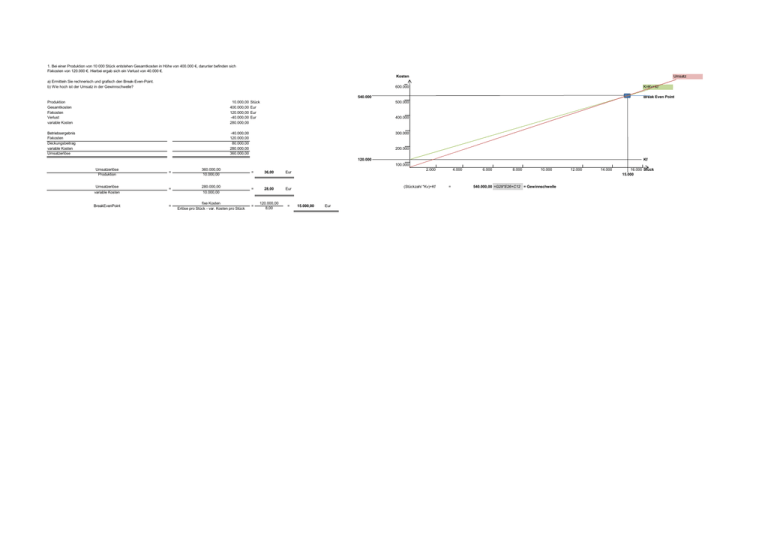
1. Bei einer Produktion von 10 000 Stück entstehen Gesamtkosten in Höhe von 400.000 €, darunter befinden sich
Fixkosten von 120.000 €. Hierbei ergab sich ein Verlust von 40.000 €.
Kosten
a) Ermitteln Sie rechnerisch und grafisch den Break-Even-Point.
b) Wie hoch ist der Umsatz in der Gewinnschwelle?
Umsatz
600.000
K=Kv+Kf
540.000
Produktion
Gesamtkosten
Fixkosten
Verlust
variable Kosten
10.000,00
400.000,00
120.000,00
-40.000,00
280.000,00
Betriebsergebnis
Fixkosten
Deckungsbeitrag
variable Kosten
Umsatzerlöse
-40.000,00
120.000,00
80.000,00
280.000,00
360.000,00
Stück
Eur
Eur
Eur
Break Even Point
500.000
400.000
300.000
200.000
120.000
Kf
100.000
Umsatzerlöse
Produktion
=
360.000,00
10.000,00
=
36,00
Eur
Umsatzerlöse
variable Kosten
=
280.000,00
10.000,00
=
28,00
Eur
BreakEvenPoint
=
fixe Kosten
Erlöse pro Stück - var. Kosten pro Stück
=
120.000,00
8,00
=
2.000
(Stückzahl *Kv)+Kf
15.000,00
Eur
4.000
=
6.000
8.000
10.000
540.000,00 =G29*E26+C12 = Gewinnschwelle
12.000
14.000
16.000 Stück
15.000
Ermitteln Sie die Gemeinkostenzuschlagssätze:
Kosten
Materialeinzelkosten
=+ Materialgemeinkosten
=+ Fertigungseinzelkosten
=+ Fertigungsgemeinkosten
= Herstellkosten
=+ Verwaltungs- und Vertriebsgemeinkosten
= Selbstkosten
Gemeinkostenzuschlagssätze in
%
Kosten in €
146,25
21,95
21,26
27,63
217,09
75,98
293,07
MEK
MGK
FEK
FGK
HK
VwGK / VtGK
SK
+
+
+
=
+
=
146,25
21,95
21,26
27,63
217,09
75,98
293,07
15,01 =E8*100/E7
MGK*100/MEK
129,96 =E10*100/E9
FGK*100/FEK
35,00 =E12*100/B11
VeGK/VtGK*100/HK
Erläutern Sie den Begriff Fixkostendegression. Stellen Sie diesen Effekt grafisch dar.
Die Fixkostendegression ist eine Abnahme der Fixkosten (die fixen Stückkosten) pro getätigte Leistungseinheit bei steigender Beschäftigung.
Die Fixkostendegression in die Kostentheorie. SIe sagt aus dass die gesamten fixen Kosten bei gestiegener Ausbringung auf eine größere Menge von
Kostenträgern verteilt werden und als folge dessen die Stückkosten rückläufig verlaufen (Kostenverlauf).
Die Fixkostendegression, auch Beschäftigungsdegression genannt, bennzeichnet das Sinken der fixen Kosten pro Stück mit zunehmender Beschäftigung. Je
größer die Beschäftigung ist, desto niedriger sind die fixen Kosten pro Stück.
Stückkosten / Preis
Nachfrage des Marktes
Fixkostendegression
produzierte Menge in Stück
Ein Unternehmen verkaufte 5 000 Pumpen und erzielte hierbei einen Umsatz
von 600.000 €. Die Fixkosten beliefen sich in diesem Zeitraum auf 200.000 €,
die variablen Stückkosten betrugen 70 € je Pumpe.
Durch den Markteintritt eines neuen Mitbewerbers kann zurzeit nur noch ein
Verkaufspreis von 105 € je Pumpe erzielt werden. Aufgrund des Preisverfalls
überlegt die Geschäftsführung, diese Pumpe aus dem Produktionsprogramm
zu nehmen. Was würden Sie der Geschäftsführung empfehlen?
5.000,00
600.000,00
200.000,00
70,00
105,00
Pumpen
Umsatz in Euro
Kf
kv
Euro MaxErlösMarktpreis
Umsatzerlös
variable KostenDeckungsbeitrag
fixe KostenErgebniss
Break-Even-Point:
Break-Even-Point =
=
=
525.000,00 zum MaxErlösMarktpreis
350.000,00 5000*70
175.000,00
200.000,00
-25.000,00 Verlust
fixe Kosten / Erlöse pro Stück - variable Kosten pro Stück
5.714,29
5.714 Stück
Der Break-Even-Point wäre hier bei 5.714 Stück.
Die Produktion dieser Pumpen trägt mit 87,5% (also die 175.000,00) zur Deckung der fixen Kosten bei.
Somit hat das Unternehmen die Aufgabe Ihren Vertrieb zu erweitern um 14,28% zu erhöhen und auch die Beschaffung der Vormaterialien auf die Probe zu
stellen ob da nicht Optimierungspotential durch neuauswahl der Lieferanten herrscht.
Bruttoverkaufspreis
Skonto
USt
Gewinnaufschlag
799,00
127,57
671,43
13,17
658,26
59,84
598,42
799,00
2,00
19,00
10,00
Euro
%
%
%
Der Bruttoverkaufspreis eines Produktes beträgt 799,00 €. Das Unternehmen
gewährt ein Skonto von 2 %. Die Umsatzsteuer beträgt 19 %. Der Gewinnaufschlag beträgt 10 %. Wie hoch sind die Selbstkosten des Produkts?
Bruttoverkaufspreis
-USt
Nettovrkaufspreis
Skonto
Barverkaufpreis
-Gewinnaufschlag
Selbstkostenpreis vom Umsatz
Der Selbstkostenpreis vom Umsatz beträgt 598,42 Euro
Blechstärke
2
4
5
8
Äquivalenz- ziffer
1
2
2,5
4
Ein Walzwerk stellt vier Arten von Blechplatten her. Die Kosten der Blechplatten unterscheiden sich durch ihre Stärke. Die jeweiligen Stärken sind:
A: 2 mm, B: 4 mm, C: 5 mm, D: 8 mm
Bestimmen Sie die Äquivalenzziffern für die vier Blechplattenarten.
Produkt
A
B
C
D