2. Stegreifaufgabe aus der Mathematik, Klasse 7c, 05.05.2015

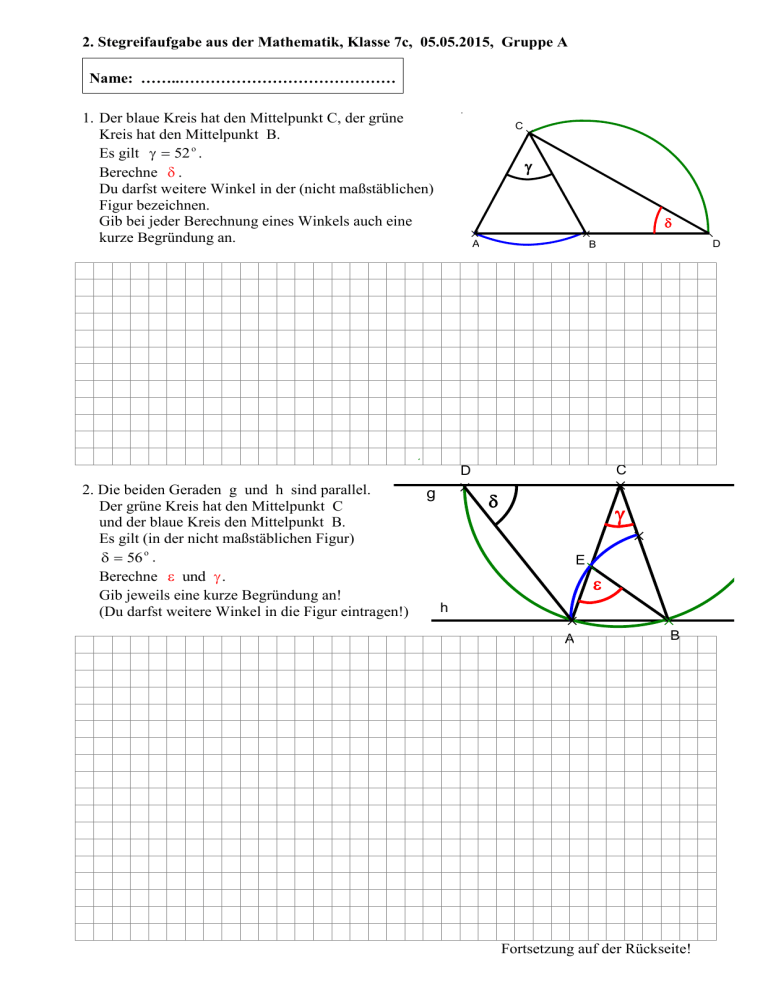
2. Stegreifaufgabe aus der Mathematik, Klasse 7c, 05.05.2015, Gruppe A
Name: ……..……………………………………
1. Der blaue Kreis hat den Mittelpunkt C, der grüne
Kreis hat den Mittelpunkt B.
Es gilt   52 o .
Berechne  .
Du darfst weitere Winkel in der (nicht maßstäblichen)
Figur bezeichnen.
Gib bei jeder Berechnung eines Winkels auch eine
kurze Begründung an.
C
g
d
A
D
B
E
C
D
2. Die beiden Geraden g und h sind parallel.
Der grüne Kreis hat den Mittelpunkt C
und der blaue Kreis den Mittelpunkt B.
Es gilt (in der nicht maßstäblichen Figur)
  56 o .
Berechne  und  .
Gib jeweils eine kurze Begründung an!
(Du darfst weitere Winkel in die Figur eintragen!)
g
d
g
E
e
h
A
B
B
Fortsetzung auf der Rückseite!
C
3. Das Bild zeigt ein gleichschenkliges
Dreieck ABC mit der Basis [AB].
Es gilt:   2    15 o
Berechne ß.

A
Aufgabe
1
2
3
Summe
Punkte
5
7
5
17

B
Erreichte Punkte
Gutes Gelingen! G.R.
2. Stegreifaufgabe aus der Mathematik, Klasse 7c, 05.05.2015, Gruppe B
Name: ……..……………………………………
1. Der blaue Kreis hat den Mittelpunkt C, der grüne
Kreis hat den Mittelpunkt B.
Es gilt   56 o .
Berechne  .
Du darfst weitere Winkel in der (nicht maßstäblichen)
Figur bezeichnen.
Gib bei jeder Berechnung eines Winkels auch eine
kurze Begründung an.
C
g
d
A
D
B
E
C
D
2. Die beiden Geraden g und h sind parallel.
Der grüne Kreis hat den Mittelpunkt C
und der blaue Kreis den Mittelpunkt B.
Es gilt (in der nicht maßstäblichen Figur)
  54 o .
Berechne  und  .
Gib jeweils eine kurze Begründung an!
(Du darfst weitere Winkel in die Figur eintragen!)
g
d
g
E
e
h
A
B
B
Fortsetzung auf der Rückseite!
C
3. Das Bild zeigt ein gleichschenkliges
Dreieck ABC mit der Basis [AB].
Es gilt:   2    25 o
Berechne ß.

A
Aufgabe
1
2
3
Summe
Punkte
5
7
5
17
Erreichte Punkte

B
2. Stegreifaufgabe aus der Mathematik, Klasse 7c, 05.05.2015, Gruppe A
C
1. 1  2 (  ABC gleichschenklig)
2  (180o  ) : 2  (180o  52o ) : 2  64o
(Winkelsumme im Dreieck ABC)
3   (  DCB gleichschenklig)
64o  2  3    2     32o
(Außenwinkel im Dreieck DCB)
g
j3
E
d
j2 j4
j1
A
D
B
C
D
2. 56 o    1 (  DAC gleichschenklig)
g
d
56    2 ( Wechselwinkel)
o
g
3  180o  (2  1 )  180o 112o  68o
E
68  3   (  EAB gleichschenklig)
o
e
j1
68  3  4 (  ABC gleichschenklig)
o
j2
h
j4
j3
  180o  2 3  180o  2  68o  44o
(Winkelsumme im Dreieck ABC)
B
A
C

3.   2    15 o und    (  ABC gleichschenklig)
180o        2    15 o  2    15 o   (Winkelsumme im  ABC)
180o  5    30 o  5    210 o    42 o und und   2  42o  15o  69o
B

A
B
2. Stegreifaufgabe aus der Mathematik, Klasse 7c, 05.05.2015, Gruppe B
C
1. 1  2 (  ABC gleichschenklig)
2  (180o  ) : 2  (180o  56o ) : 2  62o
(Winkelsumme im Dreieck ABC)
3   (  DCB gleichschenklig)
62o  2  3    2     31o
(Außenwinkel im Dreieck DCB)
2. 54 o    1 (  DAC gleichschenklig)
g
j3
E
d
j2 j4
j1
A
D
B
C
D
g
d
54 o    2 ( Wechselwinkel)
g
3  180o  (2  1 )  180o 108o  72o
E
72 o  3   (  EAB gleichschenklig)
72  3  4 (  ABC gleichschenklig)
o
  180  2 3  180  2  72  36
(Winkelsumme im Dreieck ABC)
o
o
o
o
j1
h
j2
e
j4
j3
B
A
C

3.   2    25 o und    (  ABC gleichschenklig)
180o        2    25 o  2    25 o   (Winkelsumme im  ABC)
180o  5    50 o  5    230 o    46 o und   2  46o  25o  67o
B
A

B