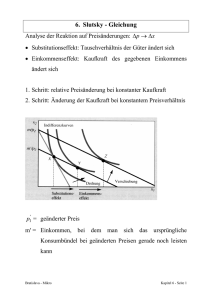
5. Die Nachfrage
Werbung

5. Die Nachfrage Æ Nachfragefunktion x1=x1(p1,p2,m) Æ komparative Statik: Was passiert, wenn sich eine Variable ändert? 5.1 Normale und inferiore Güter • ∆m → ∆x1 ? • ∆x1 >0 ∆m Bratislava - Mikro Æ normale Güter Kapitel 5 - Seite 1 • ∆x1 <0 ∆m Æ inferiore Güter 5.2 Einkommens-Konsumkurven und Engel-Kurven Æ Preise bleiben konstant Bratislava - Mikro Kapitel 5 - Seite 2 Beispiele • Perfekte Substitute angenommen: p1<p2 Æ x1=m/p1 Steigung der Engelkurve: p1 • Perfekte Komplemente Æ x1=m/(p1+p2) Bratislava - Mikro Steigung der Engelkurve: p1+p2 Kapitel 5 - Seite 3 • Cobb-Douglas Präferenzen Æ x1=a m/p1 Steigung der Engelkurve: p1/a Æ Verdoppelung von m Æ Verdoppelung von x1 Æ Verdreifachung von m Æ Verdreifachung von x1 Æ Einkommens-Konsumkurve ist ein lineare Funktion von x1 und geht durch den Ursprung (=homothetische Präferenzen) Æ realistischer: • Nachfrage steigt schneller als Einkommen (=Luxusgut) • Nachfrage steigt langsamer als Einkommen (=notwendiges Gut) Bratislava - Mikro Kapitel 5 - Seite 4 • Quasilineare Präferenzen = "parallel verschobene Indifferenzkurven" Æ mehr Einkommen ändert die Nachfrage nach Gut 1 nicht Æ kein Einkommenseffekt bezüglich Gut1 Æ Güter, die nur einen kleinen Teil des Budgets ausmachen Bratislava - Mikro Kapitel 5 - Seite 5 5.3 Gewöhnliche Güter und Giffen-Güter • ∆p → ∆x ? • ∆x1 <0 ∆p1 Æ gewöhnliches Gut • ∆x1 >0 ∆p1 Æ Giffen Gut Bratislava - Mikro Kapitel 5 - Seite 6 5.4 Preis-Konsumkurve und die Nachfragekurve • Perfekte Substitute Æ wenn p1 > p2 Æ x1=0 Æ wenn p1 = p2 Æ beliebiges x1 auf der Budgetgeraden Æ wenn p1 < p2 Æ x1=m/p1 • Perfekte Komplemente Æ x1=m/(p1+p2) Bratislava - Mikro Kapitel 5 - Seite 7 • Unteilbare Güter und Reservationspreis Vorbehaltspreis (auch Reservationspreis) = Preis, bei dem der Konsument zwischen Konsum und Nicht-Konsum indifferent ist 5.5 Substitute und Komplemente bis jetzt: perfekte Substitute und Komplemente "fast" formale Definition für Substitute und Komplemente: x1=x1(p1,p2,m) • ∆x1 >0 ∆p2 Æ Substitut • ∆x1 <0 ∆p2 Æ Komplement Bratislava - Mikro Kapitel 5 - Seite 8 5.6 Inverse Nachfrage und marginale Zahlungsbereitschaft x1=x1(p1,p2,m) (= direkte Nachfragefunktion) p1=p1(x1,p2,m) (= inverse Nachfragefunktion) 5.7 Inverse Nachfrage und marginale Zahlungsbereitschaft Optimum: MRS = p1 p2 • p1 = p2 MRS (= inverse Nachfragefunktion) • angenommen p2 = 1 und x2 = Geld für andere Güter • MRS = um welchen Geldbetrag bin ich bereit zu verzichten, um eine zusätzliche Einheit von Gut 1 zu bekommen (= marginale Zahlungsbereitschaft) Æ inverse Nachfrage mißt die marginale Zahlungereitschaft für Gut 1 Bratislava - Mikro Kapitel 5 - Seite 9