IV. Oligopolmärkte: Cournot-, Bertrand-, Stackelbergwett

IV. Oligopolmärkte: Cournot-, Bertrand-, Stackelbergwettbewerb
IV.1. Cournot-(Mengen)wettbewerb (Cournot [1838])
n ≥ 2 Anbieter stehen auf einem Markt mit inverser Nachfragekurve P(x) in
Wettbewerb. Sie entscheiden simultan über die Produktions- bzw.
Angebotsmengen x1 , ..., x n , wobei sie damit rechnen, daß sich am Markt der
markträumende Preis
p = P( x1 + ... + x n )
ergibt.
Für die Firma i ergibt dies die Profitfunktion
Π i ( x i , X −i ) = x i P( x i + X −i ) − Ci ( x i ) ,
(4.1)
wobei X −i ≡ ∑ x i als gegeben angenommen wird (Nashverhalten).
j≠i
Diese Situation entspricht einem nichtkooperativen simultanen Spiel mit
Spielermenge N = {1, ..., n}, Strategien x i ∈[0, x i ] und Auszahlungsfunktionen
Π i .1
Das Ergebnis dieses Wettbewerbs wird durch das Nashgleichgewicht des
entsprechenden Spiels beschrieben.
Jeder Spieler (Anbieter) wählt seine Strategie xi so, daß sie eine beste Antwort
(‘best reply’, ‘best response’) auf die Strategien x − i ≡ ( x1 ,..., x i −1 , x i +1 ,..., x n ) der
anderen darstellt. Die besten Antworten Ri ( x − i ) werden Best response- (Best
reply-) Korrespondenz bzw., wenn sie eindeutig sind, Reaktionsfunktion genannt.
Ein Spiel in Normalform G = (N, S, Π) ist definiert durch die Spielermenge N, dem aus den
resultierenden
Strategienraum
und
den
Strategiemengen
S = S1 × ... × Sn ,
Si
1
Auszahlungsfunktionen Π i : S → R , die für jedes mögliche Strategienprofil x = ( x1 , ..., x n ) ∈ S
angibt, welche Auszahlung jeder Spieler erhält.
IV-1
Im Falle des Cournotwettbewerbs sind diese besten Antworten durch die firstorder-conditon zu (4.1) definiert:
∂ Πi
Π ≡
=
∂ xi
P ′( x + X − i )
14i243
i
i
xi +
P( x i + X− i ) − Ci′( xi )
144
42444
3
= 0,
(4.2)
Profit einer zusätzlichen Einheit
Profitverlust bei inframarginalen Einheiten
i = 1, … , n.
Die second-order-condition ∂ 2 Π i / ∂ 2 x i < 0 ist erfüllt, wenn die Nachfragekurve
„nicht zu konvex“ gekrümmt ist (siehe die Diskussion in II.1.)
Ein Nashgleichgewicht ist als beste Antwort auf sich selbst definiert, d.h. x1 , ..., x n
ist ein Nashgleichgewicht genau dann wenn für alle i = 1, …, n gilt: xi ∈Ri ( x − i ) .
Kein Spieler kann sich in diesem Fall durch Abweichen von xi verbessern.2
(4.2) definiert n Reaktionsfunktionen xi = R( x − i ). Die Lösung dieses
Gleichungssystems ergibt das (Nash)-Cournotgleichgewicht x1NC , ..., x nNC und
n
p NC = P( X NC ), wobei X NC ≡ ∑ x i
NC
.
i =1
2
Mathematisch gesprochen bedeutet dies, daß ( x1 , ..., x n ) ein Fixpunkt der Korrespondenz
R ( x1 , ..., x n ) = ( R1 ( x −1 ), ... Rn ( x − n )) ist.
Hinreichende Bedingungen für die Existenz so eines Fixpunktes sind: i) Si ist kompakt
(abgeschlossen und beschränkt) und konvex, ii) Π i ist stetig in ( x1 , ..., x n ) und quasi-konkav in
xi . Bei endlichen Si erfüllt das entsprechende Spiel mit gemischten Strategien immer diese
Voraussetzungen. Für die durch (4.1) definierten Π i ist ii) nicht immer erfüllt. Hinreichende
Bedingungen sind z.B. C ′′ ≥ 0, P ′′ ≤ 0 .
Hinreichend für die Eindeutigkeit des Fixpunktes ist, daß R eine kontrahierende Funktion
(Kontraktion) ist, d.h.: Für alle i gilt Ri ( x −i + dx −i ) − Ri ( x −i ) < dx −i für eine Norm
z.B. erfüllt wenn
∑ ∂Ri / ∂x j dx j < max dx j . Da ∂Ri / ∂x j =
j ≠i
daß
∑ ∂Π / ∂x
j ≠i
i
i
j
j ≠i
∂Πii / ∂x j
∂Πii / ∂xi
. Ist
, ist dafür hinreichend,
< ∂Πii / ∂xi .
(Ist z.B. beim Cournotwettbewerb für n > 2 keine „problemlose“ Bedingung. Vgl. Friedman
[1977].)
IV-2
(4.2) kann umgeformt werden zu:3
p − Ci′
X
= − P′
p
p
123
1/ε
Durch
Vergleich
mit
der
inversen
m
m
Monopolmarktgleichgewicht p , x sehen wir:
i)
p NC < p m bzw.
xi
X
{
(4.3)
αi < 1
Elastizitätsregel
für
das
X NC > x m
Der Vergleich mit dem vollkommenen Wettbewerbsgleichgewicht p∗ , x ∗ ergibt
ii)
p NC > p ∗ bzw.
X NC < x ∗
Für identische Firmen reduziert sich (4.3) zu
p − C′
1
=
p
nε
n
Für Ci′ = ci folgt aus (4.3): Π = ∑ ( p − ci ) xi = p
ε
i =1
den Herfindahlindex bezeichnet.
3
IV-3
n
∑α
i =1
i
xi
H
X = pX
X
ε
(4.4)
n
wobei
H ≡ ∑α
i=1
2
i
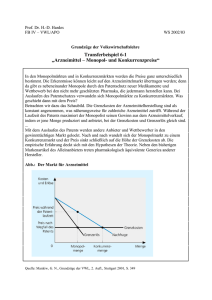
Im Falle von 2 Firmen (Duopol) kann das Cournotgleichgewicht graphisch
illustriert werden:
xj
αi
Ri ( x j )
x mj
x jNC
Rj ( x i )
α i′
xiNC
xim
xi
Für x j = 0 würde i die Monopolmenge x im wählen.
Die Steigung α i der Reaktionskurve x i = Ri ( x j ), i = 1,2, erhalten wir durch
implizite Differentiation von (4.2):
 dx i 
∂ Π ii / ∂x j
P ′′x i + P′


=−
=−
Ri′  =
i

P′′x i + 2 P ′ − Ci′′
∂Π i / ∂x i
 dx j 
Daher gilt für Ci′′≥ 0, P ′ < 0 und P′′ ≤ 0 :
Ri′ < 0
, d.h. x i , x j sind strategische Substitute
Ri′ < 1
, d.h. das Nashgleichgewicht ist eindeutig (Vgl. FN 2)
IV-4
(4.5)
Die Profitsituation der Firma i kann anhand der Isoprofitlinien diskutiert werden.
Den höchsten Profit erreicht i, wenn er auf x j mit x i = Ri ( x j ) antwortet. Für
x i < Ri ( x j ) bzw. x i > Ri ( x j ) kann i das Profitniveau Π i ( Z ) nur erreichen, wenn
j Marktanteile abgibt, d.h. wenn x j < x j . Dies erklärt die Form der Isoprofitlinien.4
Mit absteigendem x j nimmt i’s Profitniveau zu. In x im erreicht es das
Monopolprofitniveau Π i ( x im ) .
4
Formal: dx j
dxi
=−
Π = constant
wenn x i <, =, > Ri ( x j )
∂ Π i / ∂ x i ∂ Π i / ∂ xi
=
>, =, < 0
∂ Πi / ∂ x j
− xi P ′
(Benütze (4.2) und ∂ 2Πi / ∂xi2 < 0 ).
IV-5
Im Cournotgleichgewicht sieht daher die Profitsituation der beiden Firmen wie
folgt aus.
xj
Ri ( x j )
x mj
Π j (N)
x jNC
Πi ( N )
Rj ( x i )
xiNC
xim
xi
Die Profitsituation in N ist nicht effizient. Alle Allokationen in der schraffierten
Linse würden ein „besseres“ Profitergebnis bringen. (Spielraum für Absprachen
bzw. Kollusion zur Marktaufteilung, z.B. durch x i = x j = x m / 2) .
IV-6
IV.2. Stackelberg-Mengenführerschaft (Stackelberg [1934])
Gegeben die Menge xi des leaders i, wählt follower j seine Menge xj=Rj (xi).
Entscheidungssituation des leaders:
max Π i ( x i , x j )
s. t. x j = R j ( xi ) ,
xi
wobei Π i und Rj wie in IV.1 diskutiert.
Dies ergibt die Bedingung erster Ordnung:
∂ Πi
∂ Πi
+
R ′j = 0 .
∂ xi
∂ xj
Da gemäß (4.1) Π i = x i P( xi + x j ) − Ci ( xi ) , ist diese Bedingung äquivalent zu:
xi P ′ (1 + R ′j ) + P − Ci′ = 0
bzw.
xi + x j
P − Ci′
xi
= − P′
(1 + R′j )
P
P 3 xi + x j
1424
123
1/ε
αi
Beachte: −1 < R ′j < 0
IV-7
(4.6)
Graphische Illustration
xj
Ri ( x j )
Πi ( N )
x Sj
Π i ( S)
xi
xiS
Profitvergleich:
Rj ( x i )
Πi (S) > Πi ( N )
Π j (S) < Π j ( N )
Also leader sein ist besser als follower sein (gilt weil xi und xj strategische
Substitute sind. Bei strategischen Komplimenten wollen keinesfalls beide leader
sein. Siehe z.B. das Problem der Preisführerschaft, Kapitel VI.2.2.).
IV-8
IV.3. Bertrand-(Preis)wettbewerb (Bertrand [1883])
IV.3.1. Preiswettbewerb bei konstanten Grenzkosten und homogenem
Gut
n ≥ 2 Firmen bieten ein homogenes Gut an. Die Nachfragekurve nach diesem Gut
ist x(p). Die Grenzkosten sind konstant und zwar c1, ..., cn.
Die Firmen treten in Preiswettbewerb. Wenn die von ihnen gesetzten Preise p1, ...
pn sind, entfällt auf Firma i die Nachfrage
 x ( pi ),
wenn

xi ( p1 ,..., pn ) = α i x ( pi ), wenn
0,
wenn

n
mit α i > 0, ∑ α i = 1
i =1
und
pi < p−min
i
min
=
pi p− i
pi > p−min
i
{ }
p−min
i ≡ min p j .
j ≠i
Das Nashgleichgewicht pB des simultanen nichtkooperativen Preissetzungsspiels
(Bertrandgleichgewicht) ist wie folgt charakterisiert:
Fall 1: identische c1 = ... = cn.
Für alle i mit xi >0, mindestens jedoch für zwei Firmen, gilt piB = c . (Also für
Duopol (n = 2) ist p1B = p2B = c das einzige Nashgleichgewicht.)
Grund: pi < c bringt Verlust. pi > c wird unterboten und bringt keinen Markt.
Angenommen pi = c und pj > c für j ≠ i , dann würde pi nach p−min
i −ε
abweichen und trotzdem den Markt behalten. Also mindestens für 2 Firmen pi
= pj = c. Die Tatsache, daß bei oligopolistischem Preiswettbewerb bereits im
Duopol (n = 2) die effiziente Lösung (Grenzkostenpreis + Nullprofit)
zustandekommt, wird auch Bertrandparadox genannt.
Fall 2: ci < cj für alle j ≠ i und c j ≤ c k , k ≠ i, j .
Firma i bekommt den Markt.
Falls p m ( ci ) < c j , ist p B = p m ( ci ) und Π i = Π m (ci ) .
Falls p m (ci ) ≥ c j , gilt p B → c j und Π i → ( c j − ci ) x ( c j ).
( p m ( ci ), Π m ( ci ) bezeichnen Monopolpreis bzw. Monopolprofit bei
Grenzkosten ci. p B → c j bedeutet, daß ein diskretes Preisraster unterstellt wird
und p B der am knappsten unter c j liegende Preis ist.)
Grund: Jede andere Firma würde durch Unterbieten von cj Verlust machen. Ein
Preis über cj kann profitabel unterboten werden, so daß es zu so einem Preis
keine Nachfrage gibt.
IV-9
Das Bertrandparadox hat verschiedene Antworten provoziert, die zeigen, wieso
doch nicht schon bei 2 Firmen das vollkommene Wettbewerbsergebnis
zustandekommt, nämlich bei: Preiswettbewerb mit Kapazitätsgrenzen (IV.3.2.,
IV.4.), Kollusion (V.) und Produktdifferenzierung (VI.).
IV.3.2.
Preiswettbewerb
bei
steigenden
Grenzkosten
Kapazitätsschranken (Edgeworth [1897])
bzw.
Fall 1: 2 Firmen Ci′( x ) = C ′j ( x ) = c aber nur für x ≤ x i , x j .
pi = p j = c ist kein Nashgleichgewicht,
wenn x ( c ) > max{x i , x j } . Denn Abweichen auf ~
pi > c ergibt
x (~
p , c ) > 0 und Π i > 0 .
i
i
Fall 2: 2 Firmen mit Ci ( x ) = C j ( x ) = C( x ) mit C ′′( x ) > 0 .
 x( p* ) 
pi = p j = p* = C ′ 
 ist kein Nashgleichgewicht
 2 
(außer x(p) wäre unendlich elastisch in p*).
Abweichen auf ~
pi > p j = p∗ lohnt sich. Denn für j bleibt x(p*)/2 die bei pj = p*
profitmaximale Menge, so daß für i eine Residualnachfrage x R ( ~
pi ) mit x ′R < 0
5
*
*
und x R ( p ) = x( p ) / 2 verbleibt. Der resultierende Profit ist
Πi ( ~
pi , p* ) = p~i x R ( ~
pi ) − C ( x R ( ~
pi )) .
Ableitung nach ~
pi ergibt
∂ Πi
= xR ( ~
pi ) + ~
pi − C ′ ( x R ( ~
pi )) x R′ ( ~
pi ) .
~
∂ pi
[
]
5
xR ist die Nachfragekurve auf dem der Firma i verbleibendem Markt, nachdem j zu einem
bestimmten Preis (im vorliegenden Fall p* ) Nachfrage in einem bestimmten (im vorliegenden
Fall x(p*)/2) befriedigt hat. Die genaue Form von xR hängt vom Rationierungsschema ab, das
festlegt, welche Kundschaft bei Rationierung zuerst bedient wird. Die hier benötigten
Eigenschaften
x R′ < 0 und xR (p*)= x (p*)/2 sind jedoch nicht vom speziellen
Rationierungsschema abhängig.
IV-10
Also
∂ Πi
∂~
pi
=
~
pi = p*
x ( p* )  *
x ( p∗ )
pi ) > 0
+ p − C ′ 2   x ′R ( ~

23 144
12
42444
3
>0
0
und daher ist es profitabel zu einem ~
pi > p* abzuweichen. (Zwar geht der
marginale Konsument verloren; dieser hat aber ohnehin Kosten in Höhe des Preises
p * verursacht [second-order effect]. Dafür höherer Profit durch höheren Preis bei
inframarginalen Konsumenten [first-order effect].)
Graphische Illustration:
x R ( p)
~
pi
pi = p *
pj = p *
~
xi x ( p*)
x( p*)
2
2
Schlußfolgerung:
i) Bei Kapazitätsschranken oder steigenden Grenzkosten stellt der
Grenzkostenpreis kein (Bertrand-)Nashgleichgewicht dar (kein Bertrandparadox
mehr). Oligopolistischer Preiswettbewerb führt zu Preisen, die über den
Grenzkosten liegen.
ii) Wie das (Bertrand-)Nashgleichgewicht aussieht hängt im allgemeinen vom
zugrundeliegenden Rationierungsschema6 ab und auch davon, wie groß die
vorhandene (Gesamt)kapazität im Vergleich zur Marktnachfrage ist. Es kann auch
sein, daß überhaupt kein Bertrand-Nashgleichgewicht existiert.
6
Dieses legt fest, welche Kundschaft bei rationierter Nachfrage bedient wird, z.B. diejenige mit
der höchsten Zahlungsbereitschaft (effiziente Rationierung), oder diejenige, die bereit ist, sich
anzustellen (Rationierung über Warteschlangen), oder eine zufällig ausgewählte (proportionale
Rationierung).
IV-11
Das nachfolgende Beispiel 1 zeigt, daß auf einem Markt mit „mäßigen
Überkapazitäten“ kein Gleichgewicht existiert. Beispiel 2 zeigt, daß bei „kleinen
Kapazitäten“ der zur Vollauslastung führende Preis ein eindeutiges
Bertrandgleichgewicht darstellt.
Beispiel 1: Nichtexistenz eines Bertrandgleichgewichtes bei mäßigen
Überkapazitäten (Vgl. Basu, S. 41/42)
2 Firmen mit Grenzkosten Ci′ = C ′j = c und Kapazitätsgrenzen x i , x j , so daß
x ( p m (c)) < x i , x j < x (c) < x i + x j .
(pm(c) bezeichnet den Monopolpreis bei
Grenzkosten c und Nachfragekurve x(p)).
Angenommen pi = pj = c sei ein Nashgleichgewicht:
Abweichen zu ~
p > c profitabel, weil trotzdem positive Residualnachfrage
i
verbleibt ( x ( c ) > x j ).
Angenommen pi = pj > c sei ein Nashgleichgewicht:
Wegen x (c) < xi + x j ist zumindest eine Firma nicht ausgelastet. Für sie ist
ein Abweichen zu einem niedrigeren Preis profitabel.
Angenommen pi > pj ò c sei ein Nashgleichgewicht:
Wenn j ausgelastet ist, muß laut Annahme pj < pm(c) sein, so daß ein
Abweichen nach ~
p j > p j profitabel ist.
Wenn j nicht ausgelastet ist, muß laut Annahme pj > c sein und Firma i ohne
Nachfrage sein. Es ist daher für i profitabel zu einem pi mit c < ~
pi < p j
abzuweichen. Q.E.D.
IV-12
Beispiel 2: Bertrandgleichgewicht bei „knappen“ Kapazitäten
(Vgl. Tirole 5.3.2.1 und 5.7.2.1)
Markt mit inverser Nachfragekurve P(x) . 2 Firmen mit Ci′ = C ′j = c und kleinen
Kapazitäten x i , x j , so daß x ( c ) > x i + x j aber auch x Rm,i > x i und x Rm, j > x j , wobei
x Rm,i die Monopolmenge auf dem Residualmarkt bezeichnet, der i verbleibt,
nachdem j die Kapazitätsmenge x j auf den Markt gebracht hat (analog ist x Rm, j
definiert).
π
(
Π i x R ,i , x j
)
x Rm,i
xi
In dieser Situation ist der kapazitätenräumende Preis pi = p j = p B = P( x i + x j )
ein eindeutiges Nashgleichgewicht:7
Keine Firma hat wegen der ausgelasteten Kapazität einen Anreiz, den Preis zu
senken.
Firma i hat keinen Anreiz, den Preis zu erhöhen, da x i auf dem i verbleibenden
Residualmarkt x R,i eine bindende Restriktion darstellt. i würde ohne diese
Restriktion ja x Rm,i > x i , also pi < p B wählen. (Analoges gilt für j).
π
(
)
Π i pi , p B = ( pi − c) x R,i ( pi )
pm
pB
7
pi
Man beachte, daß die Gültigkeit dieser Aussage nicht vom verwendeten Rationierungsschema
abhängt.
IV-13
IV.4. Ex ante Kapazitätswahl und ex post Preiswettbewerb.
Neufundierung des Cournotgleichgewichts.
(Kreps/Scheinkman [1983])
Beispiel 2 in IV.3.2. zeigt, daß auf einem Duopolmarkt mit inverser
Nachfragekurve P(x) und bei „kleinen“ Kapazitäten x i , x j der kapazitätsräumende
Preis
p B = P ( xi + x j )
ein eindeutiges Bertrandgleichgewicht darstellt.
Dies impliziert Profitfunktionen
Π i ( xi + x j ) = xi P( xi + x j ) − cx i − c0 xi ,
die exakt die Form der Profitfunktionen beim Cournotwettbewerb haben (siehe
4.1). c0 bezeichnet die Investitionskosten.
Dies suggeriert folgendes 2-stufiges Spiel:
Stage 1: i, j wählen simultan die Kapazitäten x i , x j
Stage 2: i, j wählen simultan die Preise pi , p j bei gegebenen Kapazitäten
xi , x j .
Falls x i , x j klein genug gewählt würden, könnte man das Gleichgewicht dieses
Spiels durch backward induction wie folgt lösen:
Da in Stage 2 das einzige Gleichgewicht p B = P( xi + x j ) ist, läuft das Spiel in
Stage 1 auf ein Cournotmengenspiel hinaus. Das teilspielperfekte Gleichgewicht
dieses 2-stufigen Spiels würde so mit dem Cournotgleichgewicht zusammenfallen,
wobei die Gleichgewichtsmengen xi NC , x jNC als Kapazitäten interpretiert werden
müssen.
IV-14
Problem:
Es ist nicht garantiert, daß im Kapazitätsspiel die Kapazitäten tatsächlich so „klein“
gewählt werden, daß im Preisspiel p B = P( xi + x j ) ein eindeutiges Gleichgewicht
ist.
Ad hoc Lösung:
Hinreichend hohe Investitionskosten c0 .
Allgemeine theoretische Lösung:
Kreps und Scheinkman (1983) haben gezeigt, daß unabhängig von der Höhe der
Investitionskosten c0 bei konkaven Nachfragefunktionen ( P ′′ ≤ 0 ) und effizienter
Rationierung8 das einzige teilspielperfekte Gleichgewicht des 2-stufigen Spiels mit
Kapazitätswahl und folgendem Preiswettbewerb das Cournotergebnis ist, also
xi = x iNC , x j = x jNC und p = P( xi + x j ).
8
Effiziente Rationierung bedeutet, daß zuerst diejenigen mit der höheren Zahlungsbereitschaft
bedient werden. Die Residualnachfrage ist in diesem Fall
x(p ) − x j
x R,i (p i ) =  i
0
, wenn x(p i ) > x j
, sonst .
x ( p)
xj
xR,i
pi
pj
xj
x R,i ( pi )
IV-15