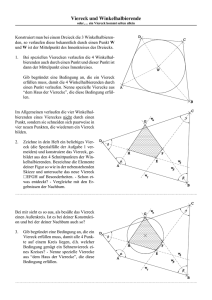
06 Geometrie
Werbung

Materialien zum Modellversuch: Vorschläge und Anregungen zu einer veränderten Aufgabenkultur (6) Zum Themengebiet Geometrie (Schwerpunkt Jahrgangsstufe 8) Vorschlag Nr. 6.1: Firmenlogos ............................................................................. 3 Einführung oder Vertiefung von Symmetriebetrachtungen anhand verschiedener Firmenlogos Vorschlag Nr. 6.2: Haus der Vierecke ................................................................... 5 Wiederholung bekannter und Einführung neuer Vierecke mit dem Ziel der Systematisierung Vorschlag Nr. 6.3: Projekt Vierecke ..................................................................... 7 Selbstständige Erarbeitung der Eigenschaften verschiedener Vierecke Vorschlag Nr. 6.4: Was muss gegeben sein, um ein ... konstruieren zu können? .................................................................................................................... 8 Untersuchung der notwendigen Stücke, um ein Viereck eindeutig konstruieren zu können Vorschlag Nr. 6.5: Flächeninhaltsformel des Parallelogramms ......................... 9 Selbstständige Erarbeitung der Flächeninhaltsformel des Parallelogramms Vorschlag Nr. 6.6: Mathematische Erkundung eines Neubaugebietes ............ 11 Fächerübergreifende und handlungsorientierte Behandlung von geometrischen Figuren im Alltag Vorschlag Nr. 6.7: Kino- und Theatersäle .......................................................... 12 Einstieg in die Behandlung von Sätzen am Kreis Vorschlag Nr. 6.8: Umfang des Fahrradreifens ................................................. 14 Näherungsweise Bestimmung von Vorschlag Nr. 6.9: Körpereigenschaften ............................................................. 15 Anhand einer Tabelle sollen verschiedene Körper auf selbstgewählte Eigenschaften untersucht werden Vorschlag Nr. 6.10: Verpackungen ..................................................................... 16 Anhand von Verpackungen sollen Körper auf ihre unterschiedlich großen Oberflächen und dem damit in der Realität damit verbundenen Materialverbrauch untersucht werden Vorschlag Nr. 6.11: Toblerone-Packung ............................................................. 17 Untersuchung der Toblerone-Packung (mit Variationen) zur Anwendung der Volumenformel von Prismen Vorschlag Nr. 6.12: Gelenkvierecke ................................................................... 18 Mithilfe eines selbstgebauten Pantographen sollen Zeichnungen vergrößert bzw. verkleinert werden Vorschlag Nr. 6.13: Maßstäbe.............................................................................. 19 Anhand verschiedener Bilder sollen Maßstäbe geschätzt werden Vorschlag Nr. 6.14: Fliegende Häuser................................................................. 20 Verbindung von geometrischen Figuren in der Architektur Vorschlag Nr. 6.15: Parkette ................................................................................ 21 Bei Parkettierungen wird die ästhetische Komponente der Mathematik besonders deutlich Vorschlag Nr. 6.16: Scheibenwischer .................................................................. 23 Beobachtung von Mechanismen mit Gelenkvierecken in der Realität und Simulation am Computer Vorschlag Nr. 6.17: Aufgaben zur Anwendung ................................................. 24 Sammlung verschiedener Aufgaben zur Anwendung geometrischer Inhalte Die Arbeit entstand im Rahmen des BLK-Modellversuchsprogramms "Steigerung der Effizienz des mathematisch-naturwissenschaftlichen Unterrichts", das vom Bund und den Ländern gefördert wird. 2 Vorschlag 6.1: Firmenlogos 1. Wie ist dieses Logo aufgebaut? Beschreibe es so genau, dass dein Nachbar es zeichnen könnte, ohne es zu sehen. 2. Wie groß sind Inhalt und Umfang bestimmter Teilflächen? 3. Ist dieses Logo schön? Begründe deine Antwort möglichst vielfältig. Quelle: Hörniger, E.: Firmenlogos. In der BLK-Lieferung vom November 1999 3 Firmenlogos: Anregungen für den Unterrichtseinsatz Ziele: Einführung oder Festigung von Symmetrieeigenschaften Am Ende einer Einheit als praktische Anwendung des Gelernten Vernetzungen Variationen der Aufgabe: (2) Inhalt und Umfang absolut und auch relativ – als Anteil bzw. Prozentsatz – zur Gesamtfläche Schüler produzieren selbst Logos aus geometrischen Figuren Schüler suchen selber zusätzliche Firmenlogos oder ein Arbeitsblatt mit weiteren Logos wird ausgeteilt (siehe vorne) Welche Logos sind dargestellt? Gibt es Gemeinsamkeiten bzw. Unterschiede? Wie groß ist der Anteil an achsensymmetrischen (punktsymmetrischen) Figuren (als Bruch oder in Prozent)? Fächerverbindenes Arbeiten mit Kunst bedenken (Mögliche) Lösungen: Anhand von Logos verschiedener (Automobil-)Konzerne lassen sich Symmetriebetrachtungen durchführen. Das folgende Diagramm verdeutlicht die dabei möglicherweise interessanten Aspekte bei der Behandlung des BMW-Logos. Das BMW-Logo besteht aus vier Kreissegmenten und einem äußeren konzentrischem Kreis mit größerem Radius. Der äußere Kreis nimmt ca. 56%, die Kreissegmente jeweils 11% der Gesamtfläche ein. Da sowohl Punkt- als auch Achsensymmetrie vorliegt und sich infolgedessen ein „harmonisches“ Bild bietet, wird das Logo i.a. als schön empfunden. ... Eignung, (mögliche) Methoden: Einzel- bzw. Partnerarbeit (Umfangreichere) Hausaufgabe Rückmeldungen von (Modellversuchs-)Lehrern: „Die Schüler waren sehr motiviert. Die Hausaufgabe, weitere Firmenlogos o.ä. zu finden, wurde von den Schülern mit großer Beispielvielfalt erledigt.“ 4 Vorschlag 6.2: Haus der Vierecke a) . d) . c) b) 1. Übertrage die oben abgebildeten Teilfiguren in dein Heft. 2. Ergänze sie jeweils zu einem Viereck. Welche Möglichkeiten findest du? Welche besonderen Vierecke kannst du jeweils herstellen? 3. Ordne den jeweiligen Figuren (eventuell mit Hilfe einer Formelsammlung) den zugehörigen Standard-Namen zu. 4. Überlege Dir, welche Charakteristika die Vierecke aufweisen. Du kannst für deine Mitschüler dazu “Steckbriefe“ aufschreiben, z.B.: Gesucht ist ein Viereck mit vier rechten Winkeln. Welche Möglichkeiten gibt es? Gesucht ist ein Viereck, bei dem jeweils zwei gegenüberliegende Seiten parallel sind. 5. Aufgabe 4 zeigt dir, was verschiedene Vierecke gemeinsam haben und was sie unterscheidet. Versuche nun, die Vierecke nach gewissen Eigenschaften zu sortieren. Beginne mit dem Quadrat. 5 Haus der Vierecke: Anregungen für den Unterrichtseinsatz Ziel: Wiederholung bekannter und Kennenlernen neuer Vierecke Verbalisierung / Beschreibung von Eigenschaften Eigenständige Klassifizierung durch die Schüler Erkenntnis, dass verschiedene Klassifizierungen möglich sind Variationen der Aufgabe: Verwendung eines Nagel- oder Geobrettes Vierecke in Gruppen anfertigen und ausschneiden lassen. Zur Ergebnissicherung Vierecke auf Moosgummi vorbereiten (Moosgummi haftet über Stunden an der Tafel, wenn man es leicht befeuchtet). Gruppen stellen ihre Ergebnisse vor. Ergänzung: „Welche Drei- oder Vierecke lassen sich mit zwei gegebenen kongruenten Dreiecken legen?“ Kann auch auf kongruente rechtwinklige Dreiecke beschränkt werden. (Mögliche) Lösungen: Ordnungsprinzipien: Vierecke mit einem, zwei oder vier rechten Winkeln, Anzahl der von einander unabhängigen Besonderheiten, Anzahl der zur eindeutigen Konstruktion benötigten Stücke Eignung, (mögliche) Methoden: Anfangs Einzelarbeit, dann Partner- bzw. Gruppenarbeit Präsentation der Ergebnisse durch die Schüler (z.B. in Gruppen an der Tafel) Rückmeldungen von (Modellversuchs-)Lehrern: „Die Schüler-Reaktionen waren positiv. Sie waren überrascht, wie viele Möglichkeiten zum Ergänzen es gibt“ 6 Vorschlag 6.3: Projekt Vierecke Alternativ zu Vorschlag 6.2 bietet sich an, dass die Schüler arbeitsteilig Eigenschaften verschiedener Vierecke (z.B. Trapezeigenschaften) erarbeiten und im Anschluss daran ihre Ergebnisse präsentieren. (Vgl. Reiß, Angelika: Das Projekt „Vierecke“ in einer 8.Klasse, in: MU (1999) Heft 6, S. 23-31.) Projekt Vierecke: Anregungen für den Unterrichtseinsatz Ziel: Verschiedene Unterrichtsmethoden (auch Gruppenarbeit) Vielfältige Schüleraktivitäten Wahl einer adäquaten Darstellung der erarbeiteten Inhalte Eignung, (mögliche) Methoden: Projektarbeit über einen längeren Zeitraum Overhead: Schüler fertigen Folien an Auch für schwächere Lerngruppen Expertengruppe (s.u.) Rückmeldungen von (Modellversuchs-)Lehrern: „Es wurden drei Stunden gearbeitet, danach erfolgte die Präsentation (sieben Stunden). Die Schüler haben gut zusammengearbeitet, teilweise auch am Nachmittag zu Hause. Es wurden vielfältige Arbeitsmaterialien eingesetzt (Arbeitsblätter, Folien mit der Hand gezeichnet oder am Computer erstellt, Tafel). Der mathematische Gehalt einiger Vorträge war sehr dürftig“ „Schüler kritisieren sich untereinander“ „Lernen ist ernsthafter, müssen Produkt vorstellen“ „Bei der Einführung der Flächeninhaltsformel für Parallelogramm, Trapez, Dreieck und Raute hat sich bewährt, in einer Doppelstunde die Methode »Expertengruppe« zu verwenden. Vorgehen: Jeder Schüler bekommt eine zufällig gezogene Spielkarte (Skatspiel); es werden Expertengruppen gebildet (7er und 8er Parallelogramm; 9er und 10er Dreieck, etc.), die sich (z.B. aus dem Schulbuch) ihr Expertenwissen aneignen, aufschreiben, wie die Herleitung geht, und Übungsaufgaben dazu heraussuchen (und lösen). Dauer: ca. 30 Minuten. Danach werden vier Gruppen (Herz, Karo, Pik, Kreuz) gebildet, in denen jetzt Experten für alle Formeln sitzen. Diese Experten haben nacheinander die Aufgabe, den anderen der Gruppe ihre Formel nahe zu bringen und die Aufgaben zu stellen. Je Gruppe ca. 10 Minuten. Hausaufgabe: Eintrag ins Regelheft (z.T. bereits während der Gruppenarbeit) und die Flächeninhaltsberechnung eines n-Ecks, das durch Zerlegen in o.g. Teilflächen zerfällt.“ 7 Vorschlag 6.4: Was muss gegeben sein, um ein ... konstruieren zu können? Was muss eigentlich gegeben sein, um ein Quadrat konstruieren zu können? Klar, es genügt die Angabe einer Seitenlänge, denn die Seiten sind alle gleich lang und wir wissen, dass alle Winkel im Quadrat 90 groß sind. Aber wie ist das beim Rechteck, bei einer Raute, bei einem Drachen...? Dabei bezeichnen wir Seitenlängen und Winkel allgemein als Stücke. Was muss gegeben sein, um ein ... konstruieren zu können?: Anregungen für den Unterrichtseinsatz Ziel: Wiederholung oder Erarbeitung von Kongruenzsätzen Vielfältige Schüleraktivitäten (Mögliche) Lösungen: - Parallelogramm: 3 Stücke (z.B.: - Trapez: 4 Stücke (z.B.: nach SWS, Rest aufgrund Parallelität) nach SWS, dann noch ein Winkel erforderlich, es sei denn Trapez ist gleichschenklig) - Rechteck: 2 Stücke (Seitenlängen, z.B.: nach SWS, wobei W 90° ist, Rest aufgrund Parallelität) - Quadrat: 1 Stück (Seitenlänge, z.B.: nach SWS, wobei W 90° und 2. Seite gleich lang ist, Rest aufgrund Parallelität) - Raute: 2 Stücke (Seitenlänge und einer der Winkel, z.B. nach SWS, wobei 2. Seite gleich lang ist, Rest aufgrund Parallelität) - Drachenviereck: 3 Stücke (z.B. nach SWS, wobei 2. Seite gleich lang ist, und dann noch eine davon verschiedene Seite nach SSS) Hierbei können insbesondere die Kongruenzsätze SWS und SSS integriert wiederholt werden. Außerdem können die S. selbst Konstruktions-Aufgaben erfinden und z.B. von anderen S. lösen lassen (eine Idee wäre: Erfinde vier Konstruktionsaufgaben, davon sollen zwei nicht eindeutig lösbar sein). 8 Vorschlag 6.5: Flächeninhaltsformel des Parallelogramms Zeichnet man ein Parallelogramm an die Tafel und fragt die Schüler nach dem Flächeninhalt, so wird man sehr schnell als Antwort a·b erhalten. Damit die Schüler eine Möglichkeit erhalten, ihre Vermutung zu überprüfen, könnte man ihnen folgenden Arbeitsauftrag erteilen: „Zeichnet ein Parallelogramm mit a = 3cm und b = 5cm und bestimmt den Flächeninhalt, indem ihr die Kästchen zählt (Kästchen links und rechts werden zu ganzen Kästchen zusammengefügt)“. b a Als alternativer Einstieg in die Unterrichtsstunde ist auch eine Abwandlung des eben erwähnten Arbeitsauftrags möglich, wobei die Schüler lediglich den Auftrag erhalten, den Flächeninhalt zu bestimmen, nicht aber auf welche Art und Weise dies geschehen soll. Da man davon ausgehen kann, dass nicht alle Schüler kongruente Parallelogramme zeichnen, ist mit verschiedenen Flächeninhalten als Lösung zu rechnen, so dass die vermutete Formel a·b verworfen werden muss. Durch die verschiedenen Lösungen wird aber die Frage aufgeworfen, welche Angaben man über ein Parallelogramm benötigt, so dass damit nur kongruente Figuren entstehen können? Bei der Diskussion mit den Schülern sollte herauskommen, dass anscheinend nicht nur die Seitenlängen, sondern auch die Höhe von Bedeutung ist und somit auch diese in die Formel zur der Berechnung des Flächeninhaltes eines Parallelogramms mit einfließen muss. Sollte an dieser Stelle keiner der Schüler eine weiterführende Idee haben, so muss man sie eventuell darauf aufmerksam machen, dass es bei einem Problem von Nutzen sein kann, wenn man versucht, es auf etwas Bekanntes zurückzuführen. In diesem Fall wäre dies der Flächeninhalt eines Rechtecks, wodurch die Schüler nun relativ schnell sehen sollten, dass man die eine Seite des Parallelogramms ’abschneiden’ kann und, wenn man sie an der anderen anfügt, ein ha Rechteck erhält mit dem Flächeninhalt ha·b b (Durchführen!!!, d.h. ein Parallelogramm a ausschneiden, teilweise abschneiden und an der anderen Seite wieder anfügen). Quelle: Michael Arendt (Gesamtschule Obersberg, Bad Hersfeld) 9 Flächeninhaltsformel des Parallelogramms: Anregungen für den Unterrichtseinsatz Ziel: Flächeninhaltsformel des Parallelogramms selbstständig ermitteln Variationen der Aufgabe: Auslegen des Parallelogramms mit kleinen Quadraten oder Dreiecken mit bekanntem Flächeninhalt (Mögliche) Lösungen: AParallelogramm = Grundseite Höhe Eignung, (mögliche) Methoden: Gruppen- bzw. Partnerarbeit Unsinnigkeit von a b mit Hilfe eines Zollstocks verdeutlichen. Dabei wird unmittelbar anschaulich klar, dass bei gleichen Seitenlängen die Flächeninhalte nicht gleich groß sein müssen. Rückmeldungen von (Modellversuchs-)Lehrern: „Auslegen mit Quadraten aufwendig“ „Kann in der Unterrichtseinheit später aufgegriffen werden“ 10 Vorschlag 6.6: Mathematischer Erkundung eines Neubaugebietes Mithilfe eines Zollstocks, einer Schreibunterlage, Papier, eines Bleistifts und eventuell eines Kassettenrecorders (für Interviews) kann man eine mathematische Erkundung eines Neubaugebietes durchführen. Ziel der Erkundung soll das Erstellen von bemaßten Skizzen, Lesen von Bauplänen und das Berechnen von auftauchenden Fragestellungen sein (z.B. Preis pro Quadratmeter etc.). (Vgl. Vaupel, Dieter: Tigerenten und Neubaugebiete, in: Praxis Schule (1996) Heft 3.) Mathematischer Erkundung eines Neubaugebietes: Anregungen für den Unterrichtseinsatz Ziel: Anwendung der gelernten Formeln Vernetzung (Gesellschaftslehre, Maßstab, Flächeninhalt, Prozentrechnung,...) Variationen der Aufgabe: Vor (oder statt) dem Ausflug in ein Neubaugebiet können zunächst ähnliche vorgegebene Aufgaben gelöst werden. z.B.: - Berechne die Größe jedes einzelnen Grundstücks - Der Grundstückpreis beträgt 62,50 DM pro m2. Wie viel muss ein Wohnungsbauunternehmen bezahlen, wenn es alle Grundstücke aufkaufen will? - Das Unternehmen will nur dann Grundstücke an Privatleute wieder verkaufen, wenn sie dabei 20% Gewinn machen. Wie teuer wären in diesem Fall die Grundstücke A2 und A5? Eignung, (mögliche) Methoden: Ausflug in ein Neubaugebiet Interviews mit Bauarbeitern Längerfristiges Projekt Als Partner- oder Kleingruppenarbeit Rückmeldungen von (Modellversuchs-)Lehrern: „außerschulischer Lernort wäre schön und motivierend“ „Die Aufgaben sind leicht, auch die %-Aufgaben und die proportionalen Zuordnungen“ (bezieht sich auf die Aufgaben aus Praxis Schule (1996) Heft 3 S. 14f.) 11 Vorschlag 6.7: Kino- und Theatersäle 1. Dir stehen nur noch Sitzplätze in der 10. Reihe des Kinos zur Verfügung. (Abstand zur 12,5 m breiten Leinwand 9,5 m) Welchen Platz wählst Du? Begründe! 2. Überlege Dir eine sinnvolle Preisstaffelung für die verschiedenen Sitze unter Berücksichtigung der aus Aufgabe 1 gewonnenen Erkenntnisse. 12 3. Im Marcellus-Theater in Rom (11500 Plätze; 11 v.Chr.; erbaut von Augustus) wurde in der gesamten dreizehnten Sitzreihe derselbe Preis verlangt, obwohl die Sitzplätze unterschiedlich weit von der Bühne entfernt waren. Was könnte der Grund dafür gewesen sein? Bühne Sitzreihe 13 Kino- und Theatersäle: Anregungen für den Unterrichtseinsatz Ziel: Einführung in die Behandlung von Winkelsätzen am Kreis Variationen der Aufgabe: Reale Pläne und Preise von Theater bzw. Kinosälen mit den in dieser Aufgabe angestellten Überlegungen vergleichen oder gar anstelle dieser beiden Beispiele einsetzen. (Mögliche) Lösungen: (1) Sinnvoll ist es einen Platz in der Mitte am Gang in Reihe 5 oder 6 zu wählen, da man dadurch fast die gesamte Leinwand im Blickfeld hat. Der Sehwinkel kann leicht ermittelt werden (Vernetzung Kongruenzsätze). Sichtbreite messen, Entfernungen vom Auge messen, Dreieck zeichnen, Sehwinkel ausmessen) (2) Von der Sitzreihe 1 bzw. 11 zur Mitte hin ansteigen. Eventuell prozentual nach dem Anteil an Leinwand im Blickfeld. Aber: Mathematik kann die Beliebtheit der Plätze nur unzureichend beschreiben. (3) Obwohl die äußeren Sitzplätze der Reihe 13 sehr nah an der Bühne waren und die inneren relativ weit weg, hatten alle aufgrund der kreisförmigen Anordnung der Sitzreihe den gleichen Anteil an Bühne im Blickfeld. Eignung, (mögliche) Methoden: Partner- oder Gruppenarbeit Vielfältige Schüleraktivitäten 13 Vorschlag 6.8: Umfang des Fahrradreifens Das glaub ich nicht. Höchstens 1,5 m so anstrengend wie das ist. „Das Rad hat einen Durchmesser von 70 cm. Mit einer Umdrehung fahren wir mindestens 2 m.“ a) Betrachte das Bild. Was meinst du, wer hat recht? b) Schätze: Wie oft passt der Durchmesser in die Strecke, die man mit einer Umdrehung zurücklegt? Überprüfe bei einem Rad, ob du richtig vermutet hast. Umfang des Fahrradreifens: Anregungen für den Unterrichtseinsatz Ziel: Experimentelle Bestimmung eines möglichst guten Näherungswerts für Variationen der Aufgabe: Untersuchung weiterer Gegenstände aus dem Alltag (z.B. Dosen, Markstücke etc.), indem man um sie ein Seil wickelt. Diskussion der Messmöglichkeiten Größe des Rades (wie üblich) in Zoll angegeben. Handelsüblich sind 26’’ (ca. 66cm) und 28’’ (ca. 71 cm) Reifen Vernetzung der Längenangaben (Mögliche) Lösungen: a) “Natürlich“ hat der Erwachsene recht, da ca. 2,2 m das richtige Ergebnis ist. b) Der Durchmesser passt genau -mal in den Umfang. Näherungsformel für die Praxis: U 3,1 d bzw. U 3 d Eignung, (mögliche) Methoden: Partnerarbeit Stationenarbeit mit verschiedenen Gegenständen 14 Vorschlag 6.9: Körpereigenschaften „Eigenschaften der Körper“ Zwei gegenüberliegende Flächen sind parallel. Alle gegenüberliegenden Flächen sind parallel. Zwei gegenüberliegende Flächen sind deckungsgleich. Die Seitenflächen stehen senkrecht zu den Grundflächen. Der Körper ist ein Prisma. Kreuzt an, auf welche Körper die vorgegebene Eigenschaft zutrifft. Überlegt euch dann selbst andere geometrische Eigenschaften Quelle: Mathematik – Denken und Rechnen 8 Hessen (1988), S. 81 (verändert). Körpereigenschaften: Anregungen für den Unterrichtseinsatz Ziel: Vertiefung von Körpereigenschaften Verbalisierung Variationen der Aufgabe: Körper bauen lassen (Strohhalme und Pfeifenreiniger) Aufgabe: Baut möglichst verschiedene Körper Analog zum Vorschlag „Haus der Vierecke“ können die Körper nach verschiedenen Kriterien klassifiziert werden So kann man auch bei Vierecken und anderen Polygonen vorgehen Eignung, (mögliche) Methoden: Partner- oder Gruppenarbeit 15 Vorschlag 6.10: Verpackungen a) Beschreibe die Körper, in denen Flüssigkeiten „verpackt“ werden b) In welchem Behälter ist die Flüssigkeit umweltfreundlich verpackt? c) Warum werden Flüssigkeiten in weniger umweltfreundlichen Verpackungen verkauft? d) Unter allen Quadern mit gleichen Volumen hat der Würfel die kleinste Oberfläche. Kennst du Lebensmittel, die in Würfelform verpackt sind? Warum sind Flüssigkeiten oft nicht in Würfelform verpackt? In dem Zehnerpack mit Orangengetränken enthält jedes Päckchen 0,2l. a) b) Der Zehnerpack kostet 1,13 €. In der 1-l-Packung kostet dasselbe Getränk 0,45€. Vergleiche! Vergleiche auch den Bedarf an Verpackungsmaterial. (Quelle: Welt der Zahl (1994), S. 103.) Verpackungen: Anregungen für den Unterrichtseinsatz Ziel: Vernetzung (Zuordnungen, Prozentrechnung) Variationen der Aufgabe: „Wie verpacke ich 20 Pralinen mit möglichst wenig Abfall?“ (siehe Aufgabe „Toblerone“) Analyse von Verpackungen, wenn z.B. die Werbung sagt: „um 20% mehr“: „Wie wird dies auf der Verpackung dargestellt?“ Eignung, (mögliche) Methoden: Material sammeln lassen Partner- oder Gruppenarbeit Vielfältige Schüleraktivitäten Gegenstände sollten präsent sein 16 Vorschlag 6.11: Toblerone-Packung 25 cm a) Was kannst du an der vorliegenden Toblerone-Packung berechnen? b) Gib 2 vierseitige Prismen mit der gleichen Höhe an, die das gleiche Volumen wie die Toblerone-Packung besitzen. Vergleiche die Oberflächen! c) Welche Prismen besitzen eine andere Höhe als die TobleronePackung und trotzdem das gleiche Volumen? Vergleiche die Oberfläche! Toblerone-Packung: Anregungen für den Unterrichtseinsatz Ziel: Anwendung der Formel zur Berechnung des Volumens von Prismen Erkennen des Zusammenhangs zwischen gleichen Volumen und unterschiedlichen Oberflächeninhalten Variationen der Aufgabe: Vergleich mit anderen Verpackungen von Süßigkeiten wie z.B. Duplo oder Hanuta. Vergleich Volumen der Verpackungen mit dem tatsächlichen Inhalt (selbst in die kompakte Hanuta-Verpackung würden theoretisch 13 statt 12 Hanutas passen!) Rückmeldungen von (Modellversuchs-)Lehrern: „Einige Gruppen benötigen Hilfestellungen bei der Suche nach einem zu dem Dreieck flächeninhaltsgleichen Viereck“ 17 Vorschlag 6.12: Gelenkvierecke Der Pantograph, der „Alleszeichner“, auch Storchenschnabel genannt, ist ein Gerät, mit dem Zeichnungen vergrößert bzw. verkleinert werden können. Versucht nicht gleich das auf dem Foto abgebildete Profimodell nachzubauen. Die Löcher haben nämlich nicht die gleichen Abstände voneinander. Deshalb baut aus Kartonstreifen mit drei bzw. zwei Löchern einen einfachen Pantographen bzw. eine Doppelraute und probiert sie aus. Die beiden folgenden Skizzen sollen euch den Bau und die Benutzung der beiden Geräte ermöglichen: Gerät 2: Gerät 1: a) Suche dir eine Zeichnung und versuche, sie wie auf dem Bild dargestellt zu vergrößern bzw. zu verkleinern. Wie vergrößert man? Wie verkleinert man? b) Versuch zu erklären, warum mit den beiden Geräten vergrößert bzw. verkleinert wird. c) In welchem Maßstab wird bei dieser Doppelraute eine Zeichnung vergrößert? d) Versucht anhand der eben angestellten Überlegungen selbst ein Gerät zu konstruieren, mit dem eine Zeichnung dreimal so groß gezeichnet werden kann. e) Schaut in eurer Umwelt, wo in alltäglichen Dingen Gelenkvierecke eine Rolle spielen, und versucht, deren Funktionsweise zu beschreiben. Quelle: MatheLive 8 (2001), S. 78f. 18 Vorschlag 6.13: Maßstäbe Schätze den Maßstab der jeweiligen Abbildung! Quelle: MatheNetz 8 (2000), S. 163. Maßstäbe: Anregungen für den Unterrichtseinsatz Ziel: Behandlung von maßstabsgetreuen Darstellungen Variationen der Aufgabe: Maßstabsgetreue Zeichnungen anfertigen (Mögliche) Lösungen: Gepard – 1 : 60 Euro – 1:1 Karte – 1 : 18000 Zelle – 1 : 8000 Chip – 2:1 Zimmer – 1 : 100 Eignung, (mögliche) Methoden: Einzel- oder Partnerarbeit 19 Vorschlag 6.14: Fliegende Häuser Die hier abgebildeten Häuser sind so konstruiert, dass sie mit einem speziellen Hubschrauber von einem Ort zum anderen transportiert werden können. Um ihnen auf dem Boden genug Standfestigkeit zu geben, gibt es in der Mittelsäule und in den Decken ein Röhrensystem, das mit Wasser gefüllt wird und so das Haus schwer genug macht. Die wassergefüllten Rohre dienen gleichzeitig als Heizungs- und Kühlsystem. a) Überlegt euch, welche Zimmerformen bei solchen sechseckigen Häusern möglich sind. b) Entwerft ein solch sechseckiges Haus in dem alle wichtigen Räume (Küche, Bad, etc.) vorhanden sind und zeichnet einen maßstäblichen Grundriss zu euren Ideen. c) Berechnet die Quadratmeteranzahl der einzelnen Zimmer und der gesamten Wohnung. d) Baut aus Pappe und anderen Materialien ein Modell eures fliegenden Hauses im Maßstab 1:50. Quelle: MatheLive 8 (2001), S. 118f. Fliegende Häuser: Anregungen für den Unterrichtseinsatz Ziel: Anwendung und Handlungsorientierung Wiederholung von n-Ecken Variationen der Aufgabe: Hausumriss vorgeben (z.B. Viereck, Trapez, etc.) und lediglich Zimmer einzeichnen lassen Eignung, (mögliche) Methoden: Partner- oder Kleingruppenarbeit Projekt- oder umfangreiche Hausarbeit 20 Vorschlag 6.15: Parkette Parkette aus Quadraten oder Rechtecken sind für den Betrachter nichts Besonderes. Aber auch Parallelogramme oder andere symmetrische Vierecke lassen sich lückenlos aneinanderlegen. Sogar mit Drachen kann parkettiert werden. Man kann aber nicht nur mit gleichartigen (d.h. untereinander kongruenten Objekten eine Ebene parkettieren, sondern auch mit verschiedenartigen geometrischen Figuren, wie z.B. mit einem großen und einem kleinen Quadrat. Wenn ihr alle Ecken mit gleichen Winkeln in derselben Farbe markiert, könnt ihr etwas über die Winkelsumme im Viereck aussagen und das hinter der Parkettierung stehende Prinzip herausfinden. a) Erklärt, wie das Prinzip der Parkettierung bei Vierecken funktioniert. Info: Es geht mit beliebigen Vierecken. b) Versucht selber eine Parkettierung der Ebene mit Vierecken zu zeichnen oder mit Papierschnipseln zu legen. c) Das nebenstehende Bild einer Parkettierung hat der Künstler M.C. Escher entworfen. Die beiden unten abgebildeten Grafiken zeigen, wie diese sogenannten Escher-Bilder aus symmetrischen Figuren entstehen. Versucht ebenfalls eine Parkettierung der Ebene mit nicht symmetrischen Figuren zu erstellen. 21 Parkette: Anregungen für den Unterrichtseinsatz Ziel: Anwendung und Handlungsorientierung Wiederholung von verschiedenen geometrischen Körpern mit dem Ziel der Parkettierung Darstellung der Mathematik als ästhetisches Mittel Variationen der Aufgabe: Untersuchung realer Parkettierungen Aus einem „Werbetext“ des Mathematikmuseums: Im Eingangsbereich des Mathematikmuseum wird ein mathematisches Kunstwerk entstehen, nämlich ein "PenroseParkett". Das ist eine besonders attraktive und interessante Überdeckung der Ebene durch "Fliesen", die erst 1974 von dem englischen Physiker und Mathematiker Sir Roger Penrose entdeckt wurde. Der Reiz dieses Parkett, das aus schmalen und großen Rauten aufgebaut ist, besteht in der Spannung aus vielen lokalen Symmetrien und seiner globalen Asymmetrie. Im Mathematikmuseum wird ein großer Ausschnitt dieses Parketts zu sehen sein, etwa 1000 Fliesen, aber die genaue Anzahl der Fliesen werden Sie bestimmen! Diese Fliesen können Sie nämlich erwerben. Die schmalen Rauten für DM 100,-.die großen für DM 200,- (oder mehr). Auf "Ihrer" Fliese kann dann auch Ihr Name stehen. Damit zeigen Sie auf Dauer Ihre Verbundenheit mit dem Mathematikmuseum. Eignung, (mögliche) Methoden: Partner- oder Gruppenarbeit Hausaufgabe Projektarbeit 22 Vorschlag 6.16: Scheibenwischer Das Skizzieren des Wischfeldes eines Scheibenwischers beim PKW (auch bei zwei Wischerblättern) ist noch relativ einfach. Schwieriger wird die Beschreibung, wie ein Wischer angetrieben wird und wie das unter der Motorhaube verborgene Gestänge aussieht. Physikalisch-mechanisch steckt hinter dem Scheibenwischermechanismus ein besonderes Kurbelgetriebe, die Kurbelschwinge, die eine Drehbewegung in eine „Hin- und Her“-Bewegung umwandelt. Die nebenstehende Skizze des Gelenkvierecks soll den Mechanismus des Scheibenwischer eines Autos darstellen. Dabei sind die Gelenke A und B fest aber drehbar gelagert. a) Konstruiere im Heft eine Figur mit folgenden Maßen: AD 3cm; AB 8cm; BC 4,5cm; CD 8,5cm. b) Wie bewegt sich die Schwinge BC (und damit der Schweibenwischer), wenn sich die Kurbel AD um A dreht? Skizziere die Bewegung der Schwinge BC! d) Konstruiere mit einem Geometrieprogramm (z.B. EUKLID) das Modell eines Scheibenwischers, der von einem Elektromotor angetrieben wird, und ermittle mit der Ortslinienfunktion den Bereich, den dein Wischermodell putzt. (Quelle: Schwarze, Monika: Von beweglichen Vierecken und Scheibenwischern, in: mathematik lehren (1997) Heft 82, S. 9-12.) Scheibenwischer: Anregungen für den Unterrichtseinsatz Ziel: Realitätsbezüge Behandlung von Gelenkvierecken Verdeutlichung von Eigenschaften geometrischer Figuren, auch mithilfe des Computers Variationen der Aufgabe: Bauen eines Modells Simulation anderer mechanischer Prozesse mit Gelenkvierecken, z.B. Eignung, (mögliche) Methoden: Partner- oder Gruppenarbeit Kleine Projektarbeit 23 Vorschlag 6.17: Aufgaben zur Anwendung 1 2 Zwei Läufer und zwei Springer eines Schachspiels stehen so auf einem Schachbrett, dass sie durch ein gedachte Verbindungslinien ein Quadrat bilden. Die Springer werden so gesetzt: zwei Felder geradeaus und eins nach rechts oder links. Du darfst zwei beliebige Schachzüge durchführen. Welche Vierecke können dabei entstehen? Die Kurbel des Wagenhebers kann so lange gedreht werden, bis das Stück d nur noch 10cm lang ist. Welche Höhe vom Boden aus kann der Punkt c höchsten erreichen? 3 Entscheide ob die Aussage wahr oder falsch ist. Begründe. (1) Jedes Quadrat ist ein Trapez. (6) Jedes Trapez ist ein Parallelogramm. (2) Es gibt Trapeze, die Rauten sind. (7) Jedes Parallelogramm ist ein Trapez. (3) Manche Rauten sind Quadrate. (8) Es gibt Quadrate, die Rechtecke sind. (4) Jede Raute ist ein Quadrat. (9) Manche Trapeze sind Quadrate. (5) Jedes Quadrat ist ein Parallelogr. (10) Manche Drachenvierecke sind Quadrate. 4 Finde die größt mögliche Anzahl von Rauten, die in dem Muster gesehen werden können. 5 Maren, Inge und Silke wohnen in der Hauptstraße Nr. 76, 77 und 79. In ihrem Matheunterricht müssen sie die Größe ihres Grundstücks berechnen. Dazu zeichnen sie jeweils einen maßstabsgetreuen Plan ihre Grundstücke. Die Maße entnehmen sie der Flurkarte. a) Wie viele Maße müssen sie mindestens bestimmen? b) Welche Art von Vierecken stellen die Grundstücke jeweils dar? d) Und dein Grundstück? e) Wie genau kann man z.B. im Maßstab 1:1000 die Längen messen? Wie groß sind die (prozentualen) Abweichungen? 24 1 Reichen Längenmessungen aus, um festzustellen, ob ein Vorfahrtsschild ein Quadrat ist? 2 Beim nächsten Schulfest will die Klasse 8c ein selbst erstelltes Quartett verkaufen. Auf den Spielkarten sind die Personen doppelt abgebildet, entweder wie in Bild 1 oder wie in Bild 2. a) Durch welche Abbildung wird jeweils der obere Teil der Karte auf den unteren abgebildet? b) Warum ist es günstiger, die Karten so wie in Bild 2 zu gestalten? 3 Welche der Fahnen sind achsensymmetrisch, welche punktsymmetrisch? 4 Entwirf ein „Parkett“ aus Rauten und Quadraten. Wähle auf Kästchenpapier ein Quadrat mit 4cm Seitenlänge, in dem du eine Grundform entwirfst. Ein Beispiel, wie das gestalten werden kann, siehst du hier. 5 In dieser Figur gibt es nur Winkel von 60° und 120°. Zeichne die Figur in dein Heft. Dabei sollen alle Strecken 2cm lang sein. Wenn du dieser Zeichnung intensiv betrachtest, kannst du auch räumliche Darstellungen erkennen. Beschreibe, was du erkennst. 6 Ideenwettbewerb: Wer entwirft das schönste Muster aus 12 bis 20 kongruenten Parallelogrammen, deren benachbarte Seiten 2cm bzw. 4cm lang sind, und bei denen die spitzen Winkel 30° betragen sollen? Zeichnet bis zu 20 Parallelogramme auf Zeichenkarton (kann auch farbig sein). Schneidet die Figuren aus und legt sie zu symmetrischen Figuren zusammen. Eine mögliche Figur seht ihr hier abgebildet (Eure Figuren müssen aber keine Pflanzen oder Tiere darstellen, sondern können auch symmetrische Muster sein). 25 1 Ein Bücherregal soll aus Holz mit mehreren Regalböden gebaut werden. a) Zunächst werden die Regalbretter und die beiden Seitenwände zurechtgesägt. Man muss darauf achten, dass die beiden Seitenwände die gleiche Länge und die Bretter alle die gleiche Breite haben. Angenommen, wir stellen das Regal so an die Wand. Steht es gut und sicher? b) Um die (rechteckige) Form zu kontrollieren, misst man am besten den Abstand von der Ecke links oben zur Ecke rechts unten und von rechts oben nach links unten. Diese beiden Maße müssen übereinstimmen. Warum? Welche Vorteile hat dieses Verfahren? c) Zur Stabilität werden meistens am Ende noch eine oder mehrere Latten diagonal an der Rückseite befestigt. Welches geometrische Prinzip steckt dahinter? 2 In ein Einfamilienhaus wird eine Treppe eingebaut. Da sie um eine rechtwinklige Ecke herumführt, müssen mehrere Stufen besonders angefertigt werden. Zeichne die Stufen maßstabsgetreu für den Steinmetz. 3 In einem Mathematik-Lexikon findet man folgende Definition des Drachenvierecks: Ein Viereck, in dem (wenigstens) zwei Paare gleich langer Nachbarseiten vorkommen, heißt Drachenviereck. Stelle alle Eigenschaften des Drachenvierecks zusammen. Mache weitere Definitionsvorschläge. 4 Überprüfe die folgenden Definitionsvorschläge für den Begriff Raute daraufhin, - ob sie den Begriff Raute auch tatsächlich definieren; - falls ja, ob sie überflüssige Forderungen enthalten. Ein Viereck heißt Raute, (1) falls die Diagonalen einander halbieren; (2) falls die beiden Diagonalgeraden Symmetrieachsen sind; (3) falls die Diagonalen orthogonal zueinander sind und einander halbieren. 5 Zeichne das Viereck A (0/0), B(12/4), C(11/11), D(4/12) in ein Koordinatensystem (1LE = 5mm). Gib die Art des Vierecks an und zeichne die Diagonalen ein. a) Was für ein Viereck entsteht, wenn du die Mittelpunkte der Seiten verbindest? b) Bestimme die Längen der Diagonalen. 26 Quellen: MatheNetz 8 (2000), Lambacher Schweitzer 8 (1996), Schnittpunkt 8 (1994), Mathematik heute 8 (1995), Zahlen und Größen 8 (2000), Mathematik 8 (1994), Die Welt der Zahl (1994), Elemente der Mathematik 8 (1994), Produktive Aufgaben für den Mathematikunterricht in der Sek. I (2001). Aufgaben zur Anwendung: Anregungen für den Unterrichtseinsatz Ziel: Übung / Anwendung Vertikale Vernetzung (Mögliche) Lösungen: Blatt (1) (1) mögliche Springerfelder: C5-F5 oder A5-H5 oder D8-E8 oder D6-E6 (jeweils weiß-schwarz) (2) ungefähr 59 cm (3) 1. w 6. f 2. w 7. w 3. w 8. w 4. f 9. w 5. w 10. w (4) a) 21 b) 2 c) schwer zu entscheiden: 3 b) 14 (5) Nr. 76 und 77 – Trapez mit 3 Maßen Nr. 79 – Rechteck mit 2 Maßen Blatt (2) (1) Ja (Seiten- und Diagonalenlängen messen) (2) a) Bild 1-Spiegelung / Bild 2-Drehung b) Man muss nur ein Bild pro Karte herstellen, da man es umgedreht aufkleben kann. (3) Deutschland – achsensymmetrisch Australien – keine Symmetrie Tansania – keine Symmetrie Jamaika – achsen- und punktsymmetrisch Israel – achsen- und punktsymmetrisch (5) Man kann – je nach Blick – zwei oder drei Würfel sehen. Blatt (3) (3) Eine Diagonale ist Symmetrieachse des Vierecks Winkelsumme ist gleich 360° ... (4) 1. keine Definition 2. Definition 3. Definition (5) Es entsteht ein Drachenviereck a) Rechteck b) BD 5,6 cm AC 7,8 cm 27