Vorlesung Teil Mechanik 2
Werbung
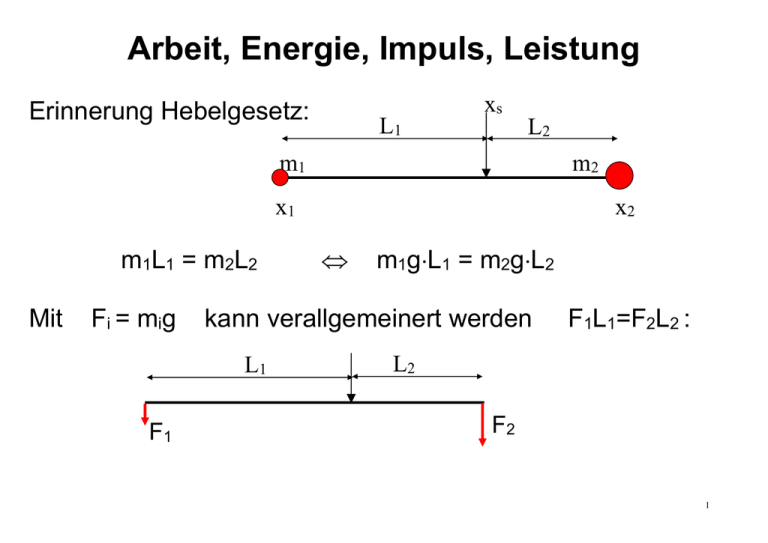
Arbeit, Energie, Impuls, Leistung xs Erinnerung Hebelgesetz: L1 L2 m1 m2 x1 m1L1 = m2L2 Mit Fi = mig m1gL1 = m2gL2 kann verallgemeinert werden L1 F1 x2 F1L1=F2L2 : L2 F2 1 Sei z.B. F1 gegeben (z.B. die Kraft, die man selber aufbringen kann) und sei L1 = 2L2 F2 = F1L1/L2 = 2F1 d.h.: Man hat eine Kraftverdoppelung. D.h. z.B., dass man doppelt so schwere Lasten heben kann, als ohne Gebrauch des Hebels. L2 L1 ABER: h2 h1 F2 F1 L1sin() = h1 und L2sin() = h2 also: h2 = h1/(L1/L2) = h1/2 L1/L2 = h1/h2 Man hebt nur die Hälfte der Strecke !!! 2 Grund: Die sogenannte Arbeit muss links und rechts die selbe sein (es wird einem nichts geschenkt!!!) Einheit: [J] Joule Bei einem räumlich konstanten Kraftfeld (z.B. Gravitation) gilt: W = Fr (Skalarprodukt von F und Abstandsvektor r) z.B. Hebe einen Gegenstand von Punkt r1=(0,0,0) nach r2=(r2x ,r2y ,r2z ) direkter Weg (1) z F r2 ein indirekter Weg (2) z r4 r3 y r2 F y x x 3 Direkter Weg (1): F = (0,0,-mg) r=r2-r1= r2 also W = (0,0,-mg)(r2x ,r2y ,r2z ) = -mgr2z Indirekter Weg (2): F = (0,0,-mg) mit r2 = r3+ r4 Zuerst von Punkt r1 nach Punkt r3 : r=r3-r1= r3 also Wteil1 = (0,0,-mg)(r3x ,r3y ,r3z ) = -mgr3z Dann von Punkt r3 nach Punkt r2 : r=r2-r3= r4 also Wteil2 = (0,0,-mg)( r2x -r3x , r2y-r3y , r2z-r3z ) = -mg( r2z -r3z) Gesamtarbeit: W = Wteil1+Wteil2 = -mgr3z -mg( r2z -r3z)= -mgr2z selbes Ergebnis: Für sog. konservative (gegenteil : dissipativ) Kraftfelder gilt, dass die Arbeit unabhängig vom Weg ist, nur Ausgangs und Endpunkt spielen eine Rolle!!! 4 Beachte: Um einen Gegenstand von a nach b zu bringen, muss man zum einen gegen das Kraftfeld anarbeiten [bzw es hilft einem]. Zum anderen muss man auch den Körper erst selber beschleunigen, aber dann wieder abbremsen. Die letzten beiden Prozesse bedeuten natürlich auch Kräfte, die sich aber in der Arbeit exakt kompensieren (zuerst muss man Arbeit aufbringen, die man beim Abbremsen aber wiedererhält). Konservative Kräfte: z.B. Gravitation, elektrostatische Kraft Dissipative Kräfte: z.B. Reibungskraft (Anschaulich: Wenn ein Körper von a nach b bewegt wird und Reibung auftaucht, dann ist es NICHT egal, wie weit der Weg ist. Je weiter der Weg ist, desto mehr Arbeit muss aufgebracht werden). 5 Bemerkung: Für räumlich nicht konstante Kraftfelder (z.B. Elektrostatik: je kleiner der Abstand zwischen geladenen Objekten, desto größer die Kraft) gilt nicht im Allgemeinen (d.h. auch für große Abstände r ) W F(r)r (allgemein) aber: Zerlegung eines Pfads in kleine Abstände dri und Aufsummieren möglich: W F (ri ) dri F (r ) dr N i 1 Was bedeutet Arbeit für den Körper, auf den sie aufgebracht wird? 6 z.B. a) Fallbeil, senkrecht stehend Hochziehen des Beils: Bei Loslassen kann das Beil Arbeit verrichten. Man hat das Beil gegen das Gravitationsfeld angehoben (Höhe h) (ein-dimensional) : W = Fr = mgh a) Fallbeil, waagerecht liegend mit Feder zu spannen Das Kraftfeld einer Feder ist F (Hook’sches Gesetz, Federkonstante D) F = -Dx ( ein-dimensional) h x F ist NICHT unabhängig vom Ort : W = Fdx = ½ Dx2 Trotzdem: Bei Entspannen der Feder kann das Beil Arbeit verrichten. 7 b) Fallbeil, waagerecht liegend, ohne Feder. Ein Verschieben des Beils in eine andere Ruheposition bewrikt nichts. Beil kann keine Arbeit verrichten. nix passiert c) Fallbeil, waagerecht liegend, ohne Feder. Wird das Beil verschoben, aber nicht in eine Ruheposition, sondern auf halber Strecke losgelassen, dann hat das Beil eine Geschwindigkeit v0. Das sich bewegende Beil kann Arbeit verrichten. v0 D.h. Manchmal kann ein ruhendes Fallbeil Arbeit verrichten, ein sich bewegendes Fallbeil kann immer Arbeit verrichten. 8 Einführung des Energie-Begriffs (Die Arbeit, die man in einen Körper steckt, erhöht die Energie des Körpers). Kann ein Gegenstand Arbeit aus einer Ruheposition verrichten: Potentielle Energie Epot z.B. im Gravitationsfeld Epot = mgh Eine bewegter Gegenstand hat Kinetische Energie Ekin= ½ mv2 Potentielle Energie und kinetische Energie können beliebig ineinander umgewandelt werden 9 z.B. Gravitationsfeld: Epot = mgh = mg ½gt2 = ½ m (gt)2 = ½ mv2 = Ekin Ganz wichtig: Energieerhaltung In einem abgeschlossenen System (es kommt nichts von Aussen hinzu und es verschwindet nichts) und bei konservativen Kraftfeldern ist die Summe aller Energien konstant!! Die Energieerhaltung kann dazu verwendet werde, um Pendel etc zu berechnen: 10 z.B.: Versuch Federpendel : Bei Auslenken der Masse m schwingt das Federpendel (Schwingungsperiode?) Je kleiner die Masse, desto schneller schwingt die Feder Energie-Erhaltung heisst hier : Summe aus a ) potentieller Energie der Gravitation mgh(t) b ) potentieller Energie der Feder ½Dh(t)2 c ) kinetischer Energie der Bewegung ½mv(t)2 ist konstant. und : dh(t ) v(t ) dt 11 also : 1 1 2 2 konst E0 mg h(t ) Dh(t ) mh 2 2 1 1 0 mgh D(2h h) m(2h h) 2 2 |:m 0 mg Dh(t ) mh(t ) d dt : h D 0 g h(t ) h(t ) m Sogenannte Differentialgleichung: Hier taucht die doppelte Abbleitung und die eigentliche Funktion auf sowie eine Konstante (g). Lösung ist : D m h(t ) A sin t g m D 12 D D cos t Beweis: h(t ) A m m und h(t ) A D sin t D m m D D D D D m g A sin t Einsetzen oben: 0 g A sin t m m m m m D Also ein schwingendes Objekt mit der Winkelgeschwindigkeit 0 D / m [ wegen (Kreisfrequenz) sin(0t) ] Schwingen tut es um die Ruheposition -(m/D)g und: je kleiner die Masse, desto größer 0 und wegen wegen T = 2/ (T Schwingungsperiode): Je größer desto kleiner T : Je kleiner m desto kleiner T 13 Versuch ballistisches Pendel Kanone schießt in Pendel Pendellänge L=1.9m Pendelmasse mp=8.5kg Kanonenmasse mk=6.7kg Geschossmasse mg=170g Laufstrecke für Kanone: D = 1m Messung: Schwingungsperiode: Tp=2.7s Laufzeit Kanone Tk=1s Auslenkung der Messstange für Winkelmessung: d=35cm 14 Es geschehen mehrere Dinge: 1) Das Geschoss verlässt die Kanone, die Kanone wird zurückgetrieben: Actio=Reactio 2) Das Geschoss trifft das Pendel, das Pendel wird ausglenkt. Teil 2: (Faden)pendel : Bei Auslenken der Masse m=mp schwingt das Fadenpendel (Schwingungsperiode?) Energie-Erhaltung heisst hier : Summe aus a ) potentieller Energie der Gravitation mgh(t) b ) kinetischer Energie der Bewegung ½mv(t)2 ist konstant. (t) L h(t) v(t) 15 Also: : 1 konst E0 mg h(t ) m[v(t )]2 2 Problem jetzt: h(t) und v(t) zeigen in verschiedene Richtungen, d.h. v(t) ist hier nicht einfach die Abbleitung von h(t). Aber man hat : h(t) = L-Lcos([t]) also: und v(t) = (t)L = Ld/dt 1 2 2 d E0 mgL[1 cos([t ])] mL 2 dt 0 mgL (t ) sin[ (t )] mL2 (t )(t ) |: mL2 (t ) g 0 sin[ (t )] (t ) L 16 Ist nicht geschlossen lösbar, aber für kleine Winkel (t) : g 0 (t ) (t ) L ist sogenannte Schwingungsgleichung g (t ) A sin t mit 0 g / L Lösung ist also: L Die Schwingungsperiode hängt nicht von der Masse ab, sondern nur von der Fadenlänge! Für die Schwingungsperiode ergibt sich im Beispiel mit L=1.9m (0 = 2.3 s-1) T = 2/0 = 2.7s ( Ergebnis siehe oben ) 17 Zusammenfassung geschlossenes System + konservatives Kraftfeld ( W F ds unabhängig vom Weg) Energieerhaltung (Summe aus potentieller und kinetischer Energie konstant) Kann z.B. für die Berechnung des Pendels verwendet werden: Ableiten der Energieerhaltung nach der Zeit ergibt 2 d x(t ) 2 2 Schwingungsgleichung : 0 0 x(t ) x(t ) 0 x(t ) 2 dt D Federpendel : m 2 0 mit der Lösung : g Fadenpendel : L 2 0 x(t) = Asin(0t) 18 Versuch : elastischer Stoss (Luftkissenbahn) v1 m v2=0 m v3=0 m v4=v1 m Ersatzweise: Versuch ClickClack / Kugelreihe Warum bleibt der erste Körper stehen und der zweite bewegt sich nach dem Stoß mit der Geschwindigkeit des ersten?? 19 Energieerhaltung würde lediglich ergeben: vor dem Stoß: E0 = ½ mv12 + 0 nach dem Stoß: E0 = ½ mv32 + ½ mv42 also : ½ mv12 = ½ mv32+½ mv42 v12 = v32+v42 keine konkrete Bedingung für v3 und v4 Es muss also zusätzliche Bedingung geben. Diese folgt aus dem 3. Newton’schen Axiom (Aktio=Reaktio) Für die Kräfte, die auf zwei Körper wirkt, gilt F1=-F2 also : F1+F2 = 0 m1a1 m2 a2 m1r1 m2 r2 0 wenn man einmal die Zeit durchintegriert, dann gilt: 20 m1 r1dt m2 r2 dt m1r1 m2 r2 m1v1 m2 v2 const Die Größe mv wird Impuls (p) genannt. Es wurde der Satz der Impulserhaltung hergeleitet: In einem abgeschlossenen System ist die Summe aller Impulse konstant. Die Impulserhaltung ergibt eine zusätzliche Bedingung (s.o.) Energieerhaltung: vor dem Stoß: nach dem Stoß: E0 = ½ mv12 + 0 E0 = ½ mv32 + ½ mv42 v12 = v32+v42 21 Impulserhaltung: vor dem Stoß: nach dem Stoß: p0 = mv1 + 0 p0 = mv3 + mv4 v1 = v3+v4 v12 = v32+2v3v4+v42 Energieerhaltung und Impulserhaltung muss erfüllt sein: Einsetzen der Impulserhaltung in Energieerhaltung: v32+v42 = v32+2v3v4+v42 0 = 2v3v4 entweder v3=0 oder nur v3=0 sein. v4=0 . Logisch kann nach Stoß Dann folgt aus Impulserhaltung: v4=v1 22 Versuch : vereinigender (vollständig inelastischer) Stoss (Luftkissenbahn) v1 m v3<v1 v2=0 2m m Ersatzweise: ClickClack mit Knetgummi oder ähnlichem zum Vereinigen der Kugeln Impulserhaltung: vor dem Stoß: nach dem Stoß: p0 = mv1 + 0 p0 = (2m)v3 v3 = ½ v1 23 Energiebetrachtung: vorher: E0 = ½ mv12 + 0 nachher: E1 = ½ (2m)v32 = ¼ mv12 Energieerhaltung gilt bei inelastischen Stößen nicht! Ein Teil der Energie wird in Wärme umgewandelt. Weiter mit der Interpretation Versuch ballistischem Pendel Kanone lief mit der Geschwindigkeit mk=6.7kg v= 1m/s zurück mg=170g = 0.17kg Impulserhaltung: 0 = mkvk –mgvg vg=vk(mk/mg)40m/s 24 Impulserhaltung bei Aufschlag ins Pendel (mp=8.5kg) mgvg + mp0 = (mg+mp)vgp vgp=vg(mg/[ mg+mp])0.8m/s d.h. Kinetische Energie des Pendels: Ekin= ½(mg+mp)vgp2 wird am Hochpunkt der Schwingung vollständig in Epot=(mg+mp)gh umgesetzt, also (mg+mp)gh = ½(mg+mp)vgp2 h = vgp2/(2g)=0.033m und also h = LLcos() (L=1.9m) =arccos(1-h/L) 10.7° L d L h 25 Die Messstange wurde d=35cm =0.35m ausgezogen. für gilt hier (Cosinus-Satz) d2 = 2L2[1-cos()] also: d2/(2L2) = 1-cos cos=1-d2/(2L2) = arccos[1-d2/(2L2)]10.6° Perfekte Übereinstimmung mit Experiment Im Prinzip kann aus der Pendelbewegung und der rückwärtslaufenden Kanone sowohl mg als auch vg bestimmt werden: ( Zwei unabhängige Versuche ) 26 Leistung (Arbeit/Energie pro Zeit) dW (t ) P(t ) dt Einheit : Watt [W] = [J/s] d.h. das kWh (Kilowattstunde) auf der Stromrechnung ist eine Energie-Einheit 1kWh = 1000Wh = 1000W(3600s) = 3.6106J = 3.6MJ Und beim Auto: 1PS = 0.7355kW 3/4kW Beispiel: Ein Mensch, der nicht viel körperlich arbeitet, nimmt am Tag Nahrungsmittel mit einem Brennwert (Energie) von ca E=2500kcal zu sich. 27 1cal entspricht der Energie, die nötig ist, um 1g Wasser von 14.5°C auf 15.5°C zu erwärmen und entspricht in Joule (also in SI-Einheiten): 4.19J = 4.19kgm2s-2 In SI-Einheiten verbraucht der Mensch pro Tag also ca W=E=10500kJ = 10.5MJ Diese Energie setzt er im Wesentlichen in Wärme um. Eine herkömmliche Glühlampe setzt nur etwa 2% der Leistung in Licht um, den Rest in Wärme. Für eine 100W Lampe (Leistung P0=100W) die konstant leuchtet gilt: dW P(t ) P0 dt W (t ) P(t )dt P0 dt P0t 28 D.h., die Energie, die eine kontinuierlich brennende 100W Lampe am Tag (t=606024s=86400s) verbraucht ist: W = P0t = 100W86400s = 8.64MJ Der Mensch verbraucht pro Tag also etwa so viel, wie eine 100W Glühlampe. Beispiel: Um seinen eigenen Körper (70kg) 1000m in die Höhe zu bewegen (Bergsteigen) benötigt man lediglich: W = mgh 70kg10m/s21000 = 700000J = 700kJ also etwa 1/10 des menschlichen Tagesverbrauchs. ABER: Wirkungsgrad ist nicht 100%. 29 Dynamik des ausgedehnten Körpers, Drehimpuls Versuch Schiefe Ebene: Zylinder verschiedener Massenverteilung aber gleicher Massen rollen unterschiedlich schnell. Massenpunktvereinfachung versagt 30 Bisher zwei Erhaltungsgrößen : Energie + Impuls Beispiel : rotierendes Rad (vereinfacht auf zwei Massepunkte mit Radius R), Winkelgeschwindigkeit 0 sei konstant. m/2 R R m v r1(t) = R(cos[0t] , sin[0t] , 0) v m/2 r2(t) = R(-cos[0t] , -sin[0t] , 0) = -r1(t) Bahngeschwindigkeiten: v1,2(t) = dr1,2/dt v1(t) = R0(-sin[0t], cos[0t], 0) v2(t) = -R0(-sin[0t], cos[0t], 0) = -v1(t) : 31 Also kinetische Energie der Rotation: E = ½(m/2)|v1(t)|2 +½(m/2)|v2(t)|2= ½m|v1(t)|2 mit Zusammenhang Bahngeschwindigkeit und Winkelgeschwindigkeit: |v(t)| = 0R ergibt sich: E = ½mR202 ist in der Tat unabhängig von t und deshalb konstant. Versuch Rotationsenergie: Mgh = ½ mR1,221,22 also: bei gleicher Energie gilt, je größer R desto kleiner 32 Impuls: p = mv1(t)+mv2(t) = mv1(t)+m[-v1(t)] = 0 Impuls ist auch konstant (nämlich 0 : Schwerpunkt des Objekts bewegt sich nicht!!) D.h. also : Energie ist 0 und konstant (Rotationsenergie), aber die Energie der Schwerpunktsbewegung (Translationsenergie) ist 0 (Schwerpunkt ruht) Frage: Gibt es einen Rotations-Impuls, der konstant aber verschieden von 0 ist? Ansatz: Bilde Vektorprodukt von r1,2 mit den einzelnen Impulsen: 33 r1([m/2]v1) = [m/2]R(cos[0t],sin[0t],0) 0R(-sin[0t],cos[0t],0) = [m/2]R20(sin[0t]0-0cos[0t], -0sin[0t]-cos[0t]0, cos2[0t]+sin2[0t]) = [m/2]R20(0,0,1) und r2([m/2]v2) = (-r1)([m/2](-v1)) = r1([m/2]v1) = [m/2]R20(0,0,1) Die Summe aus beiden Größen ergibt: r1([m/2]v1)+ r2([m/2]v2) = mR20(0,0,1) = mR2 0 34 mit vektorieller Winkelgschwindigkeit 0 : Vektor zeigt in Drehachsenrichtung. Wert ist unabhängig von der Zeit und damit konstant. r r 2 L r p mr r mr mit 2 Drehimpuls: r Drehimpulserhaltung: In einem abgeschlossenen System ist die Summe aller Drehimpulse konstant. Versuch Drehimpulserhaltung Übertragen von Drehimpuls 35 Beispiel : Fahrrad a) Ruhendes Fahrrad. Räder drehen sich nicht kein Drehimpuls. Masseschwerpunkt liegt etwa in der Mitte. von der Seite von vorne/hinten Fahrrad kippt Blauer Kreis: Schwerpunkt! Wenn das Lot vom Schwerpunkt über die Standfläche hinausragt, kippt das Objekt: Geringste seitliche Verkippung Fahrrad kippt um. 36 b) Sich bewegendes Fahrrad. Räder drehen sich. Drehimpuls 0. Ein Kippen des Rades würde zwar nicht den Betrag aber die Richtung des Drehimpulses ändern. Widerspruch zur Drehimpulserhaltung J J Drehimpuls würde sich beim Kippen verändern. Dies erfordert eine zusätzliche Kraft. Versuch Fahrradkreisel: Ein schnell rotierendes Rad bleibt aufrecht stehen. 37 Genauere Betrachtung (Vergleich der Formeln): Analogien zwischen Rotation und Translation sind möglich: Translation Größe Formel Weg s Geschwindigkeit v s Beschleunigung a s Rotation Größe Formel Winkel Winkelgeschw. Winkelbeschl. N 2 J r Masse Trägheitsmoment m i mi i 1 Kraft Drehmoment F ma M J p mv L J r p Impuls Drehimpuls 1 2 1 2 Ekin mv rot. Energie Erot J kin. Energie 2 2 ri : Abstand von der Drehachse 38 Bedeutung des Trägheitsmoments J J = ri2mi ist bei Rotation das Analogon der Masse bei translatorischen Bewegungen. Wichtig: ri ist der Abstand zur Drehachse, d.h. J ist für einen Körper unterschiedlich, je nach Drehachse, im Gegensatz zu der Masse bei einer Translation, wo die Richtung der Translation für m keine Rolle spielt!!! z y x Drehung um x und y: Massen m1= m2=m sind r1=r2=r von Drehachse entfernt (siehe fette Vektoren). Also Jx = Jy = r12m1+ r22m2= 2r2m Drehung um z : Radius ist 0 Jz=0 Objekt kann bei Drehung um z keinen Drehimpuls aufnehmen. 39 Beispiel: Schiefe Ebene Drei zylinderförmige Objekte mit Radius R und gleicher Masse m rollen eine schiefe Ebene herunter. a) Objekt ist lediglich ein Rahmen. Die eigentliche Masse ist auf der Drehachse zentriert. b) Objekt ist ein homogener Vollzylinder c) Objekt ist ein Hohlzylinder, d.h. die Masse ist auf die Aussenwand konzentiert. Der Wanddurchmesser sei sehr dünn. a) b) c) R h v 40 Am Ende der Ebene: Objekte haben Höhenunterschied h zurückgelegt, alle Objekte haben Energie E=mgh getankt. Energie verteilt sich auf eine kinetische (translative) Energie Ekin und Rotationsenergie Erot. Also für alle Fälle gilt: mgh = E = Ekin+Erot = ½mv2+½J2 Ausserdem gilt hier: Translationsgeschwindigkeit v = Bahngeschwindigkeit der Zylinderwand (Rollverhalten eines Reifens) (Erinnerung: Bahngeschwindigkeit v = R ) Fall a): Masse ist auf der Drehachse konzentriert R=0 J=0 mgh = ½mv2+0 v2 = 2gh 41 Fall b): Formelsammlung sagt : J = ½mR2 mgh = ½mv2 + ½(½mR2)2 = ½mv2 + ¼mv2 v2 = (4/3)gh Fall c): Formelsammlung sagt : J = mR2 mgh = ½mv2 + ½(mR2)2 = ½mv2 + ½mv2 v2 = gh D.h. Hohlzylinder nimmt am meisten Energie auf. Die Translationsgeschwindigkeit ist am geringsten. Noch eine nette Sache zum Trägheitsmoment: a) sei Schwerpunkt s eines Objekts bekannt und setze das Koordinatensystem so, dass s=(0,0,0) b) sei das Trägheitsmoment für eine Achse durch den Schwerpunkt bekannt 42 gesucht ist Trägheitsmoment durch eine parallele Achse: mi Ri b ri s es gilt : Punkt in der Mitte : Schwerpunkt s, Drehachse läuft senkrecht hindurch Punkt oben rechts: Anderer Punkt mit Verbindungsvektor b zum Schwerpunkt, die andere Drehachse. Punkt oben links: Massepunkt i mit Verbindungsvektor ri zum Schwerpunkt und Ri zur anderen Drehachse. Ri = ri +b 43 JR N mi Ri2 i 1 N Also: N i 1 mi Ri Ri N mi (ri b ) (ri b ) i 1 mi (ri b 2b ri ) 2 2 i 1 1 2 2 mi ri mi b 2mb m i 1 i 1 N N N m r i i i 1 Der letzte Summand ist 2mbs (Berechnung des Schwerpunkts). Da der Schwerpunkt in die Koordinate (0,0,0) gelegt wurde, fällt dieser weg und es bleibt der Satz von Steiner J R J Schwerpunkt Mb 2 : M Gesamtmasse 44 Gravitation Bisher : Erdanziehungskraft F=mg = m(0,0,-g) mit g=9.81m/s2 wobei die Erdbeschleunigung zum Zentrum der Erde zeigt. (sog. Zentralfeld) Wie groß wäre die Arbeit zum vollständigen Entfernen eines Objekts der Masse m=1kg aus dem Bereich der Erde? Arbeit ist : W = Fdr = Epot wenn dr in Richtung der Kraft zeigt, gilt : Also hier : Epot = Fdr Epot=mgdr = mgdr = mgr 45 Epot am Erdradius (Erdoberfläche) r0=6360km : Epot=6.24e7J Epot im Unendlichen : r Epot Epot – Differenz (Potentialdifferenz) Epot()-Epot(r0) d.h. man könnte einen Körper nicht aus dem Bereich der Erde entfernen absurd!! d.h. das oben angenommene Kraftgesetz F=mg kann nur eine Näherung sein, welches in der Umgebung des Erdradius gilt. Sinnvoll ist nur : Z.B. Epot() = const (z.B. 0) Epot(r) 0 Epot(r) = const/r oder Epot(r) = const/r2 etc 46 Daraus folgt für das Gravitationskraftfeld: F = dW/dr = dEpot/dr : F = -const/r2 oder -2const/r3 etc Wenn man mit diesen Kraftgesetzen versucht, z.B. Planetenbewegungen zu beschreiben, dann gibt nur F = -const/r2 zeitlich stabile Bahnen (Umkreisen der Erde um die Sonne). Aller anderen Gesetze führen entweder zum sofortigen Kollaps oder zu einer Inflation. also : F = -const/r2 wie wird die Konstante beschaffen sein? Sie beschreibt die Wechselwirkung zweier Massen, also müssen die Massen und die Stärke der WW drin sein. 47 Es zeigt sich, dass für zwei Massepunkte m1 und m2 m1m2G F 2 r oder vekto riell : gilt: m1m2G F r 3 r r ist der Abstandsvektor zwischen beiden Massen und G die Gravitationskonstante G=6.67210-11 Nm2/kg2 Wichtig: Es zeigt sich, dass exakt dieses Gesetz auch für homogene kugelförmige ausgedehnte Objekte gilt!! G ist sehr klein, also braucht man entweder winzige Abstände oder riesige Massen, damit F groß ist. was heißt „winzig Abstände“ bzw. „riesige Massen“ 48 neue Größe: Dichte d.h. für eine Kugel gilt : = m/V (Masse / Volumen) m = V = (4/3)R3 Annahme: zwei gleich große Kugeln (Radius R) mit gleicher Dichte . Wie groß ist die Kraft, wenn sich beide Kugeln berühren (also Abstand 2R) 2 4 3 G R 2 2 4 Gm1m1 4 G R 3 F 2 2 9 (2 R) 4R d.h. wenn Abstände winzig sein sollen, muss im Ausgleich die Dichte riesig werden. Höchste Dichte von Materie ist aber: Iridium 22400 kg/m3 49 Soll zwischen zwei gleich großen sich berührenden Iridiumkugeln eine Kraft von 1N wirken, dann müssen sie einen Radius von R = (9F/[4G22])1/4 = 1.615m haben. (Entspricht 400t Iridium je Kugel) Annahme: Erste Kugel habe einen Radius von r1=6378km und eine Masse von m1=5.9971024kg. Ein zweites sehr kleines Objekt (m2, r2) liegt auf der Oberfläche der ersten Kugel F = -(Gm1m2)/(r1+r2)2-(Gm1/r12)m2 = -9.83[m/s2]m2 Erdanziehungskraft !! 50 Satellit in Umlaufbahn: Kräftegleichgewicht zwischen Erdanziehungskraft und Fliehkraft? Erinnerung: Gleichförmige Kreisbewegung r(t) = R(cos[t],sin[t],0) v(t)=dr/dt=R(-sin[t],cos[t],0) a(t) = dv/dt = -2r(t) (Bemerkung: Kreisförmige Bewegung hat für einen auf der Masse ruhenden Beobachter eine sog Scheinkraft zur Folge : Er fühlt sich nach außen gezogen, Fliehkraft) F(t)=ma(t)=-m2r(t) Es ändert sich nur die Richtung: Fradial = -m2R z.B. stabile Bahn auf Höhe der Erdoberfläche: -m02R0 = -GmErdem/R02 02=GmErde/R03 T0=2/0 also T0=5057s = 84min 17sec 51 Beispiel: Bestimmung der Dichte der Sonne Fakt: 1) Erde dreht sich um Sonne in T=365.25 Tagen = 31.56106s also ist = 2/T = 210-7 s 2) wenn man den Winkeldurchmesser der Sonnenscheibe misst, dann erhält man : =0.54° rs /2 Erde R Also : tan(/2) = rs/R Dichte der Sonne : =ms/Vs ms = Vs = (4/3)rs3 Kräftegleichgewicht: GmEmS/R2=mE2R Gms/R3=2 2=G([4/3]rs3)/R3 = (4/3)Gtan3(/2) =32/[4Gtan3(/2)] = 1.4g/cm3 52 Für die Planetenbewegungen gelten aufgrund des Kraftgesetzes die drei Keplerschen Gesetze 1. Gesetz: Planeten bewegen sich in ellipsenförmigen Bahnen um die Sonne. Sonne liegt in einem Brennpunkt. 2. Gesetz: In gleichen Zeiten wird die gleiche Fläche der Ellipse überstrichen (Flächensatz, folgt aus Drehimpulserhaltung L=rp=mrv=const, d.h. wenn r klein, dann wird v groß). Planet Sonne beide Flächen sind gleich groß 3. Gesetz (Große Bahnachse)3 ~ (Umlaufzeit)2 53