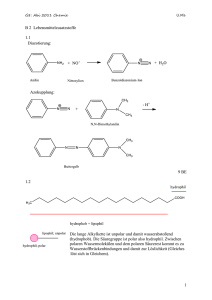
Rangsummen pro Gruppe

Nagl, Einführung in die Statistik
Seite 157
4.7 Prädiktion mit Quantils-Bereichsregeln
Der Prädikand (y) muss hier mindestens ordinales Skalenniveau haben; das ist die Voraussetzung für die
Berechnung von Quantilen.
Die Quantilsbereiche werden auf Grund der Randverteilung des Prädikanden gebildet (z.B. unterhalb des
Medians, des 1. Terzils usw. bzw. oberhalb bestimmter Quantile bzw. zwischen bestimmten Quantilen).
Implizit wird dadurch eine neues y-Merkmal gebildet, das etwa dichotom (z.B. falls die Bereichsregel darin
besteht, dass die ursprünglichen y-Werte unterhalb vs. oberhalb des Medians liegt) oder polytom ist (z.B.
trichotom, falls die Bereichsregel darin besteht, dass die ursprünglichen y-Werte unterhalb des ersten Terzils,
zwischen dem 1. Terzil und unterhalb des 2. Terzils bzw. über dem 2. Terzil liegt). Dieses neue Merkmal könnte
auch als das Quantilsbereichsmerkmal für y bezeichnet werden. Je nach Art der Formulierung des
Quantilsbereichsmerkmals ist es selbst als nominales bzw. ordinales Merkmal interpretierbar.
Für das Quantilsbereichsmerkmal können in der Folge alle Prädiktionsverfahren verwendet werden, die bisher
besprochen wurden. Auch das Prädiktor-Merkmal(x) kann in Quantilsbereiche eingeteilt werden (siehe bei den
Beispielen unten). Aus der Vielzahl dieser Art von Regeln seien hier einige in Form von Beispielen als
Anregung vorgestellt.
4.7.1 Prädiktion und Test mit Medianhalbierung
Vorgehensweise bei der Medianhalbierung für den
Prädikanden (=y):
 Berechne den Median für die gesamte
Stichprobe.
 Bilde das neue dichotome
Quantilsbereichsmerkmal mit den beiden
Ausprägungen: der Prädikand ist kleiner oder
gleich dem Median vs. größer als der Median
ist.
 Erzeuge die Häufigkeits-Kreuztabelle
Für die Prädiktion des ‚neuen dichotomen’ y könnte
eine Vielzahl der besprochenen Prädiktionsverfahren
angewandt werden (z.B. Modalregeln, a-priori-Regeln,
logistische Analysen)
Beispiel (Daten die ersten 16 Werte der Studentenuntersuchung):
Studieneintrittsalter sei der Prädikand. Prädiktor sei die Ausbildung
des Vaters. Für die diversen Ausprägungen soll prognostiziert
werden, ob der Alterswert kleiner bzw. größer als der (bzw. gleich
dem) Median ist.
Berechne den Median der 15 Alterswerte, bei denen beide Variablen
beantwortet wurden. Der Median ist dann der 8. Wert der
eindimensional sortierten Liste: 21, 21, 21, 21, 21, 21, 22, 22, ... .
med(y) = 22.
Bilde die
Kreuztabelle
Alter
zweidim.
Kreuztabelle
der Häufigkeiten < med(y)  med(y)
für die
VS, 1
0
5
5
Merkmale:
x
HS, 2
2
3
5
Abi, 3
3
0
3
Abi+, 4
1
1
2
6
9
15
Hier sei nur an die Modalregel mit dem PRE-Maß  als Regel OHNE Berücksichtigung von x: y ist größer als oder gleich
dem Median; Fehler(OHNE x)= 6/15.
eine mögliche Prädiktionsregel erinnert.
Regel MIT Berücksichtigung von x: y ist größer als oder gleich dem
Median, wenn x=VS oder HS; sonst kleiner als der Median.
Fehler(MIT x)= 3/15.  =1 – (3/6) = 0.50.
Durch Verwenden des Prädiktors: Ausbildung des Vaters kann der
Prädiktionsfehler um 50 % reduziert werden.
Problem bei der Dichotomisierung: Falls das y-Merkmal diskret ist und mehrere Werte pro Ausprägung
vorhanden sind (man spricht in diesem Falle von Ties (engl. für Bindungen) ), kann die Dichotomisierung nicht
so durchgeführt werden, dass die beiden y-Gruppen (unterhalb des Medians vs. oberhalb) gleich groß sind. In
solchen Fällen wird i. a. versucht, die Dichotomisierung so durchzuführen, dass die beiden y-Gruppen möglichst
nahe an die Gleichverteilung rankommen.
Mediantest. Im Zusammenhang mit der Fragestellung, inwiefern mit Hilfe des x-Merkmals prognostiziert
werden kann, dass in manchen Gruppen viel mehr UE unterhalb (bzw. oberhalb) des Medians liegen, steht die
Hypothese, dass der Median in allen I Gruppen (auf die Population bezogen) gleich ist:
~ 
~  
~ ( 
~ )
H0: 
1
2
I
0
Nagl, Einführung in die Statistik
Seite 158
Diese Hypothese kann in eine andere Hypothese umformuliert werden, die sich auf den Anteil der Fälle bezieht,
~ sind. Dieser Anteil sei in der i. Gruppe mit
die kleiner (bzw. kleiner oder gleich) dem Gesamtmedian 
0
 i1 bezeichnet. Dieser Anteil muss bei Geltung der Null-Hypothese in allen Gruppen gleich sein (falls keine Ties
vorhanden sind, müsste der Anteil exakt 0.50 sein, da beim Median die Gruppen halbiert werden). Daher kann
die obige Nullhypothese umgeschrieben werden:
H0: 11   21     I1 ( 1 )
Mit  1 ist der Anteil in der y-Randverteilung gemeint. Die Hypothese wird nicht mit dem Anteil von 0.50
formuliert, da eventuell Ties vorhanden sein könnten. Umgekehrt kann auch gezeigt werden, dass aus dieser
zweiten Formulierung der Nullhypothese die erste Formulierung folgt; daher sind die beiden Formulierungen
äquivalent.
Die Formulierung der MedianNullhypothese in Form der Hypothese
der gleichen Anteile in den
verschiedenen Gruppen ist die Hypothese
der stochastischen Unabhängigkeit
zwischen dem Merkmal x und dem
medianhalbierten Merkmal y.
Für den Test dieser Hypothese wurde
bereits der Chi**2 Test vorgeschlagen.
Beispiel (Fortsetzung): Die Nullhypothese, dass in der Population alle Mediane gleich
sind, entspricht dem Test der Hypothese, dass x und das medianhalbierten y
unabhängig sind. Als Test dieser Hypothese wurde der Chi**2-Test vorgeschlagen:
Die Erwartungswerte sind leider
alle kleiner als 5. Daher sollte im
vorliegenden Fall ein sogenannter
‚exakter’ Test der Hypothese verwendet werden (n zu klein in Anbetracht der vielen Zellen der
Kreuztabelle).
Häufigkeiten,
< med(y)  med(y)
Erwartungswerte
VS, 1
0, 2
5, 3
x
HS, 2
2, 2
3, 3
Abi, 3
3, 1.2
0, 1.8
Abi+, 4
1, 0.8
1, 1.2
6
9
5
5
3
2
15
Zu Übungszwecken soll der Test aber durchgeführt werden: LR2=10.69 (bei 3
Freiheitsgraden) oder P2 =7.917. Der kritische Bereich ist der  7.81. Nach beiden
Testwerten wird H0 abgelehnt.
Medianhalbierung des Prädiktors.
Auch der Prädiktor kann beim Median halbiert werden
(wiederum beim Median der gesamten Stichprobe); in diesem Fall wird auch für das x-Merkmal ein neues
medianhalbiertes x-Merkmal gebildet.
4.7.2 Andere Quantilsbereichsdefinitionen
Die gleiche Vorgehensweise wie in 4.7.1 kann für andere Einteilungen gewählt werden.
4.7.2.1
Lagefragestellung
Die Lage der Werte kann auch mit Hilfe anderer Quantile in völlig gleicher Weise wie in 4.7.1 untersucht
werden. Dies schließt auch Test der Hypothesen bezüglich der Gleichheit anderer Quantile in verschiedenen
Gruppen mit ein.
Zudem können auch Bereichseinteilungen gebildet werden, die mehr als zwei Bereiche enthalten (z.B.:
Einteilung in 3 Bereiche mit Hilfe der Terzile).
4.7.2.2
Streuungsfragestellung
Mit Quantilsbereichsdefinitionen können auch Fragestellungen bearbeitet werden, die die Streuung einer
Variablen betreffen, indem Bereiche gebildet werden, die extremen Werte (vs. den mittleren Bereich) enthalten
(z.B.: Einteilung in 2 Bereiche: ein Bereich: Werte bis zum 1. Quartil und größer als das 3. Quartil versus
innerhalb des 1. und 3. Quartils).
Nagl, Einführung in die Statistik
Seite 159
4.8 Prädiktion mit ordinalen Grad-2-Regeln
Die bisher eingeführten Prädiktionsregeln sind so formuliert, dass in jeder Prädiktionssituation genau eine UE
betrachtet wird. Aufgrund der Kenntnis des x-Wertes dieser UE wird ihr der y-Wert zugeordnet. Diese Art der
Prädiktion nennen HILDENBRAND u. a. (1975) Grad-1-Prädiktion, die dazugehörigen Regeln Grad-1-Regeln.
Diese Prädiktionskonstellation kann erweitert werden. Statt eine einzige UE zu betrachten, sollen nun jeweils
zwei UEen in einer Prädiktionssituation vorhanden sein (die i. und die j. UE). Aus der Kenntnis der x-Werte der
beiden UEen soll das ordinale Verhältnis ihrer y-Werte erraten werden. Mit ordinalem Verhältnis in y ist
gemeint, ob der y-Wert der i. UE kleiner (bzw. gleich oder größer) als der y-Wert der i. UE ist. Diese Art von
Prädiktionsregeln werden ordinale Grad-2-Regeln genannt.
Zwei Typen von ordinalen Prädiktionsregeln sollen unterschieden werden:
Typ 1: die x-Werte der
beiden UEen sind
bekannt; das ordinale
Verhältnis in y ist
gesucht.
i. UE
xi bekannt
xj bekannt
gesucht
y
o i, j
yi
Bezeichnung für den
ordinalen Vergleich, der wobei o y =
i, j
<, = oder größer sein
yj
Beispiel: Das y-Merkmal sei IQ; das xMerkmal seien Berufsgruppen. Von den beiden
betrachteten UEen sei der x-Wert der i. UE
Kellner, der x-Wert der j. UE Mechaniker.
Gesucht auf Grund der Berufgruppen das
ordinale IQ-Verhältnis: Ist der Kellner weniger,
gleich intelligent oder intelligenter als der
Mechaniker?
< wenn yi < yj
= wenn yi = yj
> wenn yi > yj
y
kann: o i , j .
Typ 2: nur das ordinale
Verhältnis der x-Werte
der beiden UEen ist
bekannt; das ordinale
Verhältnis in y ist
gesucht
j. UE
i. UE
j. UE
xi
< = > bekannt
gesucht
yi
o i, j
y
xj
yj
Beispiel: Das y-Merkmal sei IQ; das xMerkmal sei Soziale Schicht. Von den beiden
betrachteten UEen sei die Schicht der i. UE
höher als die der j. UE. Gesucht auf Grund des
ordinalen x-Verhältnisses (niedriger) das
ordinale IQ-Verhältnis: ist die i. UE auch
intelligenter als die j. UE?
Die ordinale Prädiktion erfordert nur die Ordinaleigenschaft des Prädikanden. Der erste Typ ordinaler Grad-2Prädiktion soll im folgenden für x-Merkmale angewandt werden, die als nominal betrachtet werden, der zweite
Typ soll bei ordinalen x-Merkmalen Verwendung finden.
Paarvergleichstabellen aller UEen für ein Merkmal
Damit die Möglichkeit ordinaler Grad-2-Prädiktion untersucht und beurteilt werden kann, sind Paarvergleiche
zwischen allen UEen bezüglich beider Merkmale erforderlich. Vorerst sollen die Paarvergleiche für ein
Merkmal vorgestellt werden.
Jede Untersuchungseinheit
wird mit jeder anderen
paarweise verglichen (hier
im Sinne eines ordinalen
Vergleichs bezüglich des
Merkmals y).
Der Vergleich der UE mit
sich selbst kann entfallen.
Von den insgesamt n*n-n
ordinalen Vergleichen ist
eine Hälfte zur anderen
’konter’-asymmetrisch ( das
Kleiner-Zeichen wird zum
Größer-Zeichen; und
umgekehrt)
Beispiel: Gegeben seien die y-Werte für n=5 UEen.
12, 12, 11, 11, 30
j
UE
y
i
1
2
…
n
y1
y2
...
yn
...
y
o 1, n
1
y1

y
o 1, 2
2
y2
y
o 2 ,1

...
y
o 2, n
...
...
...
...
...
...
n
yn
y
o n ,1
y
o n ,2
...

Konterasymmetrie der ordinalen
Relation (Spezialform von
Asymmetrie):
 

  
  
y
y
Wenn o i , j =   , gilt o j,i =    .
j
UE
i
1
2
3
4
5
y
12
12
11
11
30
1
2
3
4
5
12

=
<
<
>
12
=

<
<
>
11
>
>

=
>
11
>
>
=

>
30
<
<
<
<

Insgesamt sind hier bei n=5 UEen 25 - 5
Paarvergleiche vorhanden.
Die Konterasymmetrie zeigt sich etwa beim
Vergleich der 1. mit der 3. UE: > . Der Vergleich der
3. UE mit der 1. muss aber < ergeben. An den
Stellen, an denen die obere Hälfte der Vergleiche >
hat, hat die untere Hälfte der Vergleiche < an den
entsprechenden Stellen; entsprechendes gilt auch für
>. Das Gleichheitszeichen bleibt erhalten.
Nagl, Einführung in die Statistik
Seite 160
Die Tabelle der UE-Paarvergleiche kann summarisch durch Ränge (Rangplätze oder Mittelränge) beschrieben
werden bzw. könnte umgekehrt verwendet werden zur Definition von Rängen.
Die Rangplätze für ein Merkmal
y sind die Positionen in der
Reihenfolge der sortierten yWerte.
Falls manche y-Werte gleich
sind (d.h. Ties sind vorhanden),
werden jeweils die Ränge für
die gleichen y-Werte gemittelt.
Die so entstehenden Ränge sind
die Mittelränge (engl.
Meanranks oder Midranks).
Die Rangposition innerhalb yWerte y1, ... , yi ,... ,yn wird als
Rangplatz bezeichnet.
Andererseits besagen die
Rangplätze implizit, wie viele
Werte kleiner sind (plus 1, für
die eigene Position).
Mittelränge (Definition auf
Grund der ordinalen
Paarvergleiche):
Genau diese Information ist
auch in der Tabelle aller
Paarvergleiche mit enthalten:
als Anzahl der Vergleiche pro
Spalte, die Kleiner-Zeichen
haben.
Bei Vorhandensein von Ties ist
zusätzlich noch die Anzahl der
Gleichheitszeichen relevant.
Über Rangplätze mit gleichen yWerten wird gemittelt. Der so
gebildete Wert heißt
Mittelrang der i. UE : r(yi)
bzw. ri , falls der
Bezug zu y klar ist (entsprechend
bei Verwendung des Index j)
r(yj ) = 1
+ (Anzahl der Vergleiche,
für die o iy, j gleich ‚<’ ist)
+ (Anzahl der Vergleiche,
für die
y
o i , j gleich
‚=’ ist)/2;
wobei i alle UE-Nummern
sind (außer j)
Beispiel: Die y-Werte enthalten Ties (Bindungen); 11
kommt zweimal und 12 zweimal vor. Im ersten
Schritt werden fortlaufend Rangplätze vergeben.
Danach werden die Rangplätze der UEen gemittelt,
die gleiche Ränge haben:
UE
Rangplatz
j
1
yj
2
3
4
5
12 12 11 11 30
3 4 1 2 5
r(yj) 3.5 3.5 1.5 1.5 5
Mittelrang
j
UE
1
2
3
4
5
y
12
12
11
11
30
12

=
<
<
>
12
=

<
<
>
11
>
>

=
>
11
>
>
=

>
30
<
<
<
<

<
Anzahl
Vergleiche =
>
2
1
1
2
1
1
0
1
3
0
1
3
4
0
0
i
1
2
3
4
5
r1= 1 + 2 + 0.5(1) =3.5. r3= 1 + 0 + 0.5(1) =1.5.
r5= 1 + 4 + 0=5
4.8.1 Prädiktion mit ordinalen Grad-2-Regeln für nominale Prädiktoren
Für nominale Prädiktoren kann der 2. Typ ordinaler Grad-2-Prädiktion nicht verwendet werden, da der 2. Typ
auch für das x-Merkmal einen ordinalen Vergleich vorsieht; daher wird der 1. Typ von ordinalen Grad-2Prädiktion verwendet.
Die Paarvergleiche zwischen allen UEen müssen jeweils die beiden Merkmale (x und y) in den Vergleich mit
einbeziehen, bezüglich y interessiert nur das ordinale Verhältnis der UE-Paare, bezüglich x sollen die
Eigenschaften beider UEen beachtet werden (wegen Typ 1).
Beispiel: Studieneintrittsalter sei der Prädikand. Prädiktor sei die Ausbildung des Vaters (1: VS, 2: HS, 3: Abi, 4: Abi+), die vorerst als
nominales Merkmal behandelt wird. n=15.
(j)
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15)
(UE)
Die 15 UEen wurden
x, y 1, 22 1, 22 1, 24 1, 24 1, 30 2, 21 2, 21 2, 22 2, 22 2, 23 3, 21 3, 21 3, 21 4, 21 4, 23
formal nach den Codes
(1) 1, 22 
=
<
<
<
>
>
=
=
<
>
>
>
>
<
sortiert, wobei die
(2) 1, 22 =
<
<
<
>
>
=
=
<
>
>
>
>
<

Verbindung zwischen x
und y beibehalten werden
(3) 1, 24 >
>
=
<
>
>
>
>
>
>
>
>
>
>

müssen.
(4) 1, 24 >
>
=
<
>
>
>
>
>
>
>
>
>
>

(5) 1, 30 >
>
>
>
>
>
>
>
>
>
>
>
>
>

Bei den einzelnen
(6)
2,
21
<
<
<
<
<
=
<
<
<
=
=
=
=
<

Vergleichen werden die
(7) 2, 21 <
(i)
<
<
<
<
=
<
<
<
=
=
=
=
<

ordinalen
(8) 2, 22 =
=
<
<
<
>
>
=
<
>
>
>
>
<
Vergleichsergebnisse für y

in alle Zellen eingetragen
(9) 2, 22 =
=
<
<
<
>
>
=
<
>
>
>
>
<

(<, =, >).
(10) 2, 23 >
>
<
<
<
>
>
>
>
>
>
>
>
=

(11) 3, 21 <
<
<
<
<
=
=
<
<
<
=
=
=
<

Vergleiche der UE mit sich
(12)
3,
21
<
<
<
<
<
=
=
<
<
<
=
=
=
<

selbst sind nicht nötig.
(13) 3, 21 <
<
<
<
<
=
=
<
<
<
=
=
=
<

Insgesamt sind 15*15-15
(14) 4, 21 <
Vergleiche durchgeführt
<
<
<
<
=
=
<
<
<
=
=
=
<

worden.
(15) 4, 23 >
>
<
<
<
>
>
>
>
=
>
>
>
>

Nagl, Einführung in die Statistik
Seite 161
Wenn Untersuchungseinheiten gleiche Werte in beiden Merkmalen haben, können die Werte in Form einer
zweidimensionalen Häufigkeits-Verteilung in Vektorform zusammengefasst werden.
Die in den x- und y-Werten
übereinstimmenden
Wertekonstellationen (auch
Konfiguration genannt) werden
zusammengefasst und geordnet nach
den Codes von x (innerhalb gleicher x
nach y) dargestellt. Zusätzlich muss
vermerkt werden, wie oft die
Konfigurationen vorkommen
(=Häufigkeiten).
Häufigkeitsverteilung in
Vektorform:
Konfigurat Häufigk
Index
ionen
eit
x1, y1
...
xi, yi
...
xm, ym
1
...
i
...
m
n1
...
ni
...
nm
Beispiel(Fortsetzung):
Konfigurationen
i
xi, yi
1
1, 22
2
1, 24
3
1, 30
4
2, 21
5
2, 22
6
2, 23
7
3, 21
8
4, 21
m= 9
4, 23
Zweidimensionale
HäufigkeitsVerteilung in
Vektorform.
ni
2
2
1
2
2
1
3
1
1
Paarvergleiche zwischen den Konfigurationen
I. a. sind wesentlich weniger Vergleiche notwendig, wenn Paarvergleiche nur für die Konfigurationen
durchgeführt werden, sind; allerdings muss dann die zugrundeliegende Anzahl der Paar-Vergleiche der UEen
berechnet werden.
Beispiel(Fortsetzung): Paarvergleiche zwischen allen Konfigurationen.
Berechnung der Anzahl der
Paarvergleiche aller UEen auf Grund
j
1
2
3
4
5
6
Konfigurationen
der Konfigurationen:
Den gleichen Konfigurationen (in der
Diagonale) entsprechen ni*(ni-1)
Paarvergleiche zwischen den
verschiedenen UEen.
Die Anzahl der UE-Vergleiche
zwischen verschiedenen
Konfigurationen (i, j) entspricht dem
Produkt der Häufigkeiten der beiden
Konfigurationen: ni*nj.
4.8.1.1
i
1
2
3
4
5
6
7
8
9
7
8
9
x, y, n 1, 22, 2 1, 24, 2 1, 30, 1 2, 21, 2 2, 22, 2 2, 23, 1 3, 21, 3 4, 21, 1 4, 23, 1
1, 22, 2 =, 2
<, 4
<, 2
>, 4
=, 4
<, 2
>, 6
>, 2
<, 2
1, 24, 2 >, 4
=, 2
<, 2
>, 4
>, 4
>, 2
>, 6
>, 2
>, 2
1, 30, 1 >, 2
>, 2
=, 0
>, 2
>, 2
>, 1
>, 3
>, 1
>, 1
2, 21, 2 <, 4
<, 4
<, 2
=, 2
<, 4
<, 2
=, 6
=, 2
<, 2
2, 22, 2 =, 4
<, 4
<, 2
>, 4
=, 2
<, 2
>, 6 * >, 2
<, 2
2, 23, 1 >, 2
<, 2
<, 1
>, 2
>, 2
=, 0
>, 3
>, 1
=, 1
3, 21, 3 <, 6
<, 6
<, 3
=, 6
<, 6
<, 3
=, 6
=, 3
<, 3
4, 21, 1 <, 2
<, 2
<, 1
=, 2
<, 2
<, 1
=, 3
=, 0
<, 1
4, 23, 1 >, 2
<, 2
<, 1
>, 2
>, 2
=, 1
>, 3
>, 1
=, 0
Dem Vergleich der 5. Konfiguration mit der 7. entsprechen 6 (=2*3) UE-Vergleiche (siehe
Pfeile).
Die Anzahl der UE-Vergleiche zwischen verschiedenen UEen bei der 5. Konfiguration (in
der Diagonalen) sind gleich 2 (=2*(2-1)). Vergleichen Sie auch die hier verzeichnete Anzahl
mit der vorherigen Tabelle der UE-Paarvergleiche.
Gruppenpaarvergleichshäufigkeitstabelle
Damit die Möglichkeit der
komparativen Prädiktion auf
Grund der
Gruppenzugehörigkeit beurteilt
werden kann, müssen die
Paarvergleiche zwischen den
Gruppen zusammenfassend
dargestellt werden.
Symbole für die
Paarvergleichsanzahl:
n i, j = Anzahl der UEPaarvergleiche, bei denen der yWert aus der i. kleiner ist als der
y-Wert aus der j. Gruppe.
Entsprechend ebenfalls: n i, j
Für jedes Gruppenpaar kann die und n i, j .
Anzahl der verschiedenen yPaarvergleichsergebnisse (<, =
oder >) dargestellt werden.
Die Tabelle rechts stellt die
Dadurch werden die
Bezeichnungen der Vergleiche
Paarvergleiche zwischen den
zwischen diversen Gruppen dar.
UEen (bzw. den
Konfigurationen) weiter
Beispiel (Fortsetzung): In Form einer Matrix alle
Paarvergleichsergebnisse:
1
2
3
4
5
5
3
2
xGruppe ni
n
< = > < = > < = > < = >
1: VS
2: HS
3: Abi
4: Abi+
8
19
15
8
5
5
3
2
4
4
0
0
8
2
0
2
2 4 19 0
8 4 8 0
9 6 0 0
3 3 4 0
0 15 2
6 9 4
6 0 3
3 3 1
0 8
3 3
3 0
0 1
z.B. Die Anzahl der Paarvergleiche zwischen HS und Abi,
bei denen die HS-Kinder einen kleineren Alters-Wert als die
Abi-Kinder haben, ist gleich 0 = n(2,3)<.
Index
<
1
..
i
..
I
1
=
j
>
<
n(1,1)< n(1,1)= n(1,1)> … n(1,I)<
…
…
…
…
…
n(i,1)< n(i,1)= n(i,1)> … n(i,I)<
…
…
…
…
…
n(I,1)< n(I,1)= n(I,1)> … n(I,I)<
I
=
>
n(1,I)= n(1,I)>
…
…
n(i,I)= n(i,I)>
…
…
n(I,I)= n(I,I)>
Nagl, Einführung in die Statistik
Seite 162
zusammengefasst.
Eigenschaften der Gruppenpaarvergleichshäufigkeiten:
 Konterasymmetrie: n(i,j)> = n(j,i)< für alle Paare i und j.
 Bei den Vergleichen der Gruppen mit sich selbst wird die Homogenität der Gruppe untersucht (Wie
viele Vergleiche enden in Gleichheit?)
4.8.1.2
Modalprädiktionsregeln und Fehlermaße
Als Prädiktionsregeln könnten hier alle Regeln auf Paarvergleiche (damit konkret auf die
Gruppenpaarvergleichshäufigkeitstabelle) angewandt werden, die auch auf die Prädiktion von 1-GradZusammenhängen zwischen Variablen angewandt wurden.
Hier soll mit Hilfe von 2-Grad-Modalregeln auf Grund des x-Paares auf die ordinale Relation in y geschlossen
werden. Das Ergebnis entspricht der Vorgehensweise für das Lambda-Maß.
In Form einer PaarvergleichsKreuztabelle, bei der die
Paarrelation zwischen dem xMerkmal in den Zeilen der yPaarrelation als Spalten
gegenübergestellt gestellt wird,
können die
Paarvergleichshäufigkeiten
ebenfalls dargestellt werden.
Beispiel (Fortsetzung): PaarvergleichsFür jedes Gruppenpaar in der xVariablen, das durch das Indexpaar Kreuztabelle
Fehleranzahl
x-Gruppen
Alter
(i,j) identifiziert werden kann,
bei Regel
y
paare
wird eine Zeile verwendet.
i j
<
=
>
Pro Zeile werden die drei
12
8
4
8
VS VS
Gruppenpaarvergleichshäufigkeiten
2
4
19
6
VS HS
0
0
15
0
bezüglich y dargestellt.
VS Abi
VS
HS
HS
HS
HS
Abi
Abi
Abi
Abi
Abi+
Abi+
Abi+
Abi+
Für jede Zeile kann die
Modalkategorie für y-Paare
gefunden werden (<,= oder >).
In dieser Form wird der
Zusammenhang zwischen x und
y besser sichtbar.
Als Fehler (MIT x) wird nun die
Anzahl der Fehlprädiktionen
Die Modalregeln prädizieren
berechnet (das ist die Summe über
die modale y-Relation (<,= oder alle nicht prädizierten Zellen).
>)
Für die Bewertung der Güte der
Prädiktionsregeln, die x
berücksichtigen, muss als
Vergleich eine ‚Trivialregel’
herhalten.
Die OHNE x Regel ist die
Modalregel, die auf Grund der yRandverteilung gewonnen wird.
Der Fehler (OHNE x) ist dann
ebenfalls die Anzahl der
Fehlprädiktionen in der
Randverteilung.
Beispiel:
In Form eines Ordnungs-Diagramms, das
Beispiel:
die Gruppen in eine auf Grund der
Paarvergleiche gefundenen Ordnung
bezüglich y darstellt, vom kleinsten
(unten) bis zum größten Wert (oben). Eine
xGruppen
VS,
HS,
Abi,
Abi+,
1
2
3
4
8
2
8
9
3
0
0
0
0
2
4
3
1
82
46
82
2
6
12
6
6
0
6
0
3
2
6
3
1
71 MIT
128 OHNE
xy =1 - 71/128 = 0.45
HS
2
Abi Abi+
3
4
Ht.
5
5
3
2
5
5
3
2
<
<
<
<
>
<
<
>
>
>
=
>
>
<
<
<
Y: niedrig
0
4
4
6
3
0
6
6
3
0
3
3
0
In der Randzeile ist ebenfalls die Modalzelle
markiert (=Regel OHNE x). Die Summe über die
beiden nichtmarkierten Randhäufigkeiten ist der
Fehler OHNE x d.h. F(OHNE x)=128.
VS
1
Y: hoch
2
19
8
0
4
15
9
0
3
8
3
0
1
Die Modalregeln sind pro Zeile markiert. Der
Fehler MIT x ist die Summe über je zwei Zellen der
Zeile, die nicht prädiziert wird. Abschließend
werden die Fehler aus allen Zeilen summiert:
F(MIT x)=71.
Das PRE-Maß kann als Grad-2xy=1- F(MIT x) / F(OHNE x)
Lambda bezeichnet werden
Darstellung der Modalregeln
In Matrixform kann die Prädiktionsregel
für jedes Gruppenpaar dargestellt werden.
Dabei wird auch die
Konterasymmetrieeigenschaft sichtbar.
Abi+
VS
HS
Abi
Abi+
VS
HS
Abi
Abi+
VS
HS
Abi
Abi+
Die Modalausprägungen der
Paarvergleiche wurden in der
Matrix eingetragen (der
Vollständigkeit halber auch in
der Diagonalen).
VS ist ‚älter’ als alle anderen
Gruppen; Abi+ ist ‚älter’ als hS
und Abi; hS ist ‚älter’ als Abi.
Abi+
Die Einzelinformationen über
die y-Beziehung der Gruppen
zueinander werden im
Ordnungsdiagramm gebündelt.
hS
Umgekehrt kann der Vergleich
zwischen je zwei Gruppen
VS
Abi
Nagl, Einführung in die Statistik
Seite 163
direkt abgelesen werden: VS
etwa ist ‚älter’ als Abi, weil VS
über Abi angeordnet ist.
solche Darstellung wird auch als HASSEDiagramm bezeichnet.
4.8.1.3
Gruppen-Paarvergleichshäufigkeiten und Gruppen-Rangsummen
In diesem Abschnitt soll gezeigt werden, wie die Randsumme der Gruppen-Paarvergleichshäufigkeitsmatrix
verwendet werden kann, recht einfach die Gruppen nach y zu sortieren; andererseits soll gezeigt werden, dass
aus dieser Randsumme auch die Rangsumme der einzelnen Gruppen berechnet werden kann.
Zeilen- und
Spaltenrandsummen:
Für die Feststellung der
Ordnung zwischen den
Gruppen ist die
Randsumme der
GruppenPaarvergleichshäufigkeit
en hilfreich.
Zeilen-Randsumme:
I
n i,   n i, j ;
j1
analog auch für > und =.
Spalten-Randsumme:
I
n , j   n i, j ;
i 1
analog auch für > und =.
Konterasymmetrie der
Zeilen- und
Spaltenrandsummen
Interpretation: Anzahl
von ordinalen
Paarvergleichen
bestimmter Art (<, =
oder >) aller Mitglieder
einer Gruppe.
Sortieren der Gruppen
nach y ist auf Grund der
relativen Randsummen
möglich (relativ zur
Anzahl der Vergleiche
pro Gruppe)
n i, = n ,i 
xGruppe ni
n
1: VS
2: HS
3: Abi
4: Abi+
1
2
3
4
5
5
3
2
ZeilenrandSumme
< = > < = > < = > < = >
5
5
8 4
19 4
8
2
3
15 0
0
8
9
2
8
2
3
0
2
< = >
4 19 0
4 8 0
0 15 2 0
6 9 4 3
8
3
12 8 50
31 17 22
70
80
6
0
0
27 15 0
42
4
6 0
3 3
3 3
3
1 0
1
12 6 10
0
0
S.Randsumm
50 8 12 22 17 31 0 15 27 10 6 12
e
82 46 82
28
210
Für alle Ordinalrelationen (<,=,>) wurden die Zeilenrandsummen gebildet,
ebenfalls die Spaltenrandsummen.
Die Zeilenrandsumme n(1,)> = 50. Zudem ist auch in der
Spaltenrandsumme n(,1)< = 50.
Aus der Spaltenrandsumme wird ersichtlich: Die Mitglieder der Gruppe 1
(HS) sind bei allen Paarvergleichen 50 (=n(,1)< ) mal größer . Dieselbe
n , j : Anzahl von
allen Paarvergleichen,
bei denen ein Mitglied
der j. Gruppe größer ist
Für ni Mitglieder der i.
Gruppe gibt es ni(n -1)
Paarvergleiche.
Die relative
Vergleichsposition =
n i, / (ni(n -1))
Information erhält man aus der Zeilenrandsumme: n (1,)> = 50 (wegen der
Konterasymmetrieeigenschaft).
Weil die Gruppengrößen verschieden sind, müssen auch die
Vergleichssummen relativiert werden.
xGruppen
1: VS
2: HS
3: Abi
4: Abi+
ni
<
=
5
5
3
2
>
12
31
27
12
8 50
17 22
15 0
6 10
Vergleich
e
insgesamt
pro
Gruppe
70
80
42
28
Anteil der
>Vergleiche an den
Vergleichen
pro Gruppe
0.71
0.28
0
0.36
Am größten
(0.71) ist VS,
auf 2.
Position
Abi+(mit
0.36), auf der
dritten HS
(mit 0.28).
Rangsummen pro Gruppe
Zuerst werden die
Die y-Werte seien fortlaufend
Summe der
xy-Werte
y-Mittelränge
Mittelränge
Gruppen ng
Mittelränge gebildet auf nummeriert (die ersten n1
59
Grund der y-Werte.
Werte seien die der 1. Gruppe 1: VS 5 22, 22, 24, 24, 30 8.5, 8.5, 13.5, 13.5, 15
2:
HS 5 21, 21, 22, 22, 23 3.5, 3.5, 8.5, 8.5, 11.5
35.5
usw.)
3:
Abi 3 21, 21, 21
3.5, 3.5, 3.5
10.5
Die Rangsumme pro
Die Rangsumme der 1.
4: Abi+ 2 21, 23
3.5, 11.5
15
n
Gruppe ist die Summe
Gruppe: R1 =  j11 r ( y j ) .
15
Gesamtsumme
120
über die Mittelränge
innerhalb jeder Gruppe
Entsprechend können die
Die Gesamtsumme der Ränge ist auch bei Mittelrängen gleich der
Summe der Zahlen 1+2+...+n (hier ist n=15). Daher nach dem
anderen Rangsummen
GAUß’schen Schultrick (n+1)*n/2. Für n=15: 16*15/2 = 120
definiert werden
Rangsumme berechnen R = n1
(4)
1
 j1 r( y j ) kann auch
(1)
(4)/(1)
(2) (3)
auf Grund der
=(1)+(2)/2+(3)
Summe der
Rangmittel
so berechnet werden:
Zeilenrandsumme der
g
<
=
>
ng
Mittelränge
werte
Gruppenn1 + n , j + n , j /2.
11.8
1: VS 5
8 50
59
12
PaarvergleichsGenerell für die g. Gruppe:
7.1
2: HS 5
35.5
31 17 22
Häufigkeiten
3.5
3: Abi 3
0
10.5
27 15
Rg = ng + n ,g  + n , j /2
4: Abi+ 2
12
6
10
15
7.5
Nagl, Einführung in die Statistik
Seite 164
Bei den Rängen (und Rangsummen) werden auch die ‚=’ Vergleiche verwendet (allerdings nur zur Hälfte).
Damit unterschiedliche Gruppengrößen Vergleiche zwischen den Gruppen nicht beeinträchtigen, werden für den
Gruppenvergleich oft die Mittelwerte der Ränge gebildet.
4.8.2 Ordinaler Prädiktor und ordinaler Prädikand
Wenn der Prädiktor selbst auch ordinal ist, kann die Grad-2-Prädiktionsregel so formuliert werden, dass aus dem
‚kleiner-gleich-größer’ - Verhältnis der beiden Prädiktorwerte auf das entsprechende Verhältnis des
Prädikanden geschlossen wird (Prädiktionsregel des Typ 2). Bei der Übersicht über alle Vergleiche interessiert
nun bei beiden nur das ordinale Verhältnis.
4.8.2.1
Kreuztabelle der ordinalen Paarvergleiche
Zuerst ist die Berechnung der
Anzahl der Paarvergleiche aller
UEen etwa auf Grund der
Konfigurationen wie oben (bei
qualitativem Prädiktor
durchgeführt) notwendig.
Zusätzlich zur ordinalen Beziehung
in y wird hier noch die ordinale
Beziehung zwischen dem Prädiktor
(x-Merkmal) eingefügt.
Beispiel(Fortsetzung): Paarvergleiche zwischen allen Konfigurationen. Studienantrittsalter soll
nun als ordinale Information gewertet
j
Konfigurationen
x, y, n
1 1, 22, 2
2 1, 24, 2
3 1, 30, 1
i 4 2, 21, 2
5 2, 22, 2
6 2, 23, 1
7 3, 21, 3
8 4, 21, 1
9 4, 23, 1
1
2
3
Bezeichnung: Die Anzahl der
konkordanten und diskordanten
Vergleiche (kurz: c und d)
5
6
7
8
9
1, 22, 2 1, 24, 2 1, 30, 1 2, 21, 2 2, 22, 2 2, 23, 1 3, 21, 3 4, 21, 1 4, 23, 1
=,=, 2 =,<, 4 =,<, 2 <,>, 4 <,=, 4 <,<, 2 <,>, 6 <,>, 2 <,<, 2
=,>, 4 =,=, 2 =,<, 2 <,>, 4 <,>, 4 <,>, 2 <,>, 6 <,>, 2 <,>, 2
=,>, 2 =,>, 2 =,=, 0 <,>, 2 <,>, 2 <,>, 1 <,>, 3 <,>, 1 <,>, 1
>,<, 4 >,<, 4 >,<, 2 =,=, 2 =,<, 4 =,<, 2 <,=, 6 <,=, 2 <,<, 2
>,=, 4 >,<, 4 >,<, 2 =,>, 4 =,=, 2 =,<, 2 <,>, 6 <,>, 2 <,<, 2
>,>, 2 >,<, 2 >,<, 1 =,>, 2 =,>, 2 =,=, 0 <,>, 3 <,>, 1 <,=, 1
>,<, 6 >,<, 6 >,<, 3 >,=, 6 >,<, 6 >,<, 3 =,=, 6 <,=, 3 <,<, 3
>,<, 2 >,<, 2 >,<, 1 >,=, 2 >,<, 2 >,<, 1 >,=, 3 =,=, 0 =,<, 1
>,>, 2 >,<, 2 >,<, 1 >,>, 2 >,>, 2 >,=, 1 >,>, 3 =,>, 1 =,=, 0
Die Kreuztabelle der ordinalen
Symbole in der Kreuztabelle der
Paarvergleiche stellt in den Zellen ordinalen Paarvergleiche:
die Anzahl der
y
Vergleichsergebnisse dar, die
Summe
<
=
>
sowohl der Zeilen- und
< n<< n<= n<>
n<
Spaltenausprägung entsprechen. In
x = n=< n== n=>
n=
den Zeilen werden die drei x> n>< n>= n>>
n>
Vergleichsergebnisse als
Summe n< n= n>
Ausprägungen (<, =, >)
n
unterschieden, in den Spalten die
drei Ausprägungen der yn  = Anzahl der UEVergleichsergebnisse (<, =, >).
Paarvergleiche, bei denen sowohl der
erste x-Wert als auch der y-Wert
kleiner als die jeweiligen zweiten sind.
Entsprechend können ebenfalls die
anderen Paarvergleichshäufigkeiten
beschrieben werden.
Die Eigenschaft der radialen
<
=
>
Symmetrie erleichtert das
n<=
n <>
< n<<
Erstellen der Kreuztabelle, da sich
= n=<
n=
n=>
==
ein Teil der Tabelle aus dieser
Eigenschaft ergibt.
n>=
n>>
> n><
Die Randsummen selbst sind
symmetrisch.
4
Beispiel (Fortsetzung): Kreuztabelle der
ordinalen Vergleiche
Paaranzahl
<
y
=
>
<
=
>
11
17
54
16
14
16
54
17
11
Summe
81
48
81
Summe
82
46
82
210
x
n<< = 11. Von den Vergleichen zwischen
allen Paaren der UEen gilt 11 mal: sowohl
beim x-Wertepaare als auch beim yWertepaare ist jeweils der 1. Wert kleiner als
der 2. Wert.
n<> = 54. D.h. 54 mal: beim x-Wertepaar ist
der 1. Wert kleiner als der 2. Wert, aber beim
y-Wertepaare der 1. Wert größer als der 2.
Wert.
<
=
>
<
11
16
54
=
17
14
=
17
>
54
16
11
Spaltenrandsymmetrie: n< = n> und Beim Spaltenrand (unten) ist 82= n<= n>
Beim Zeilerand (rechts) ist 81= n<= n>B
Zeilenrandsymmetrie: n< = n>
Die Häufigkeit n<< (=n>>) wird als die
<
=
>
Anzahl der konkordanten, n<> (=n><)
16
< 11 =c
d=54
=
17
17
14
wird als die Anzahl der diskordanten
> 54=d
c=11
16
Vergleiche bezeichnet
Nagl, Einführung in die Statistik
Seite 165
Die Häufigkeiten können wie Fall von Grad-1-Häufigkeiten relativiert werden. Zeilen- und Spaltenanteile
erleichtern die Interpretation:
Beispiel(Fortsetzung): Als Wahrscheinlichkeit interpretiert: Falls
z.B. Prozentuierung pro Zeile.
<
=
>
<
=
>
4.8.2.2
13.6 19.8 66.7
35.4 29.2 35.4
66.7 19.8 13.6
bekannt ist, daß für das x-Paar ‚<’ gilt, gilt mit einer
Wahrscheinlichkeit von 0.667 für das y-Paar : ‚>’ .
Prädiktionsregeln, Fehlermaße und Zusammenhangsmaße
Die meisten ordinalen Zusammenhangsmaße untersuchen die sogenannte Konkordanzaussage, einfach
formuliert: ’Je größer der x-Wert, desto größer der y-Wert’. Da die x-Werte mit den y-Werten im allgemeinen
nicht direkt vergleichbar sind, kann die Konkordanzaussage nur in Form einer UE-Paarvergleichsaussage exakt
formuliert werden, etwa (A und B seien zwei UEen):
‚Hat A einen kleineren (bzw. größeren) x-Wert als B,
<
<
so hat A auch einen kleineren (bzw. größeren) y-Wert als B’: xA > xB  yA > yB
Etwas abgeschwächt postuliert die Konkordanzaussage, dass bei Vergleichen zwischen zwei UEen die Anzahl
der konkordanten Vergleiche (n<<) weit größer als die Anzahl der nicht konkordanten (n< >) ist.
Unterschiedliche Art der Berücksichtigung der Gleichheit der Paare führt zu verschiedenen
Zusammenhangsmaßen.
Die gebräuchlichsten Zusammenhangsmaße für ordinale Merkmale verwenden im Zähler die Differenz
zwischen der Anzahl konkordanter und diskordanter Vergleiche ( n   n   ):
Name
Formel
n   n  
n (n  1) / 2
KENDALLs a
KENDALLs b
n   n  
(n   n    n  )( n   n    n  )
n   n  
n (min( I, J)  1) /(2 min( I, J))
STUARTs c
2
n   n  
n   n  
GOODMAN-KRUSKALs 
KIMs d x y  SOMERs d x y
n 
n   n  
 n    (n   n  ) / 2
Beispiel (Ausbildung des Vater und
Studienantrittsalter):
11  54
= -0.4095
15 (151) / 2
11 54
(11 54  16)(11 54  17)
11  54
152 ( 41) /( 2*4)
= -0.52762
= -0.5096
11  54
= -0.6615
11  54
11 54
= -0.52761
11 54  (1617) / 2
KIMs d x y  SOMERs d x y
n   n  
(n   n    n  )
1154
= -0.5309
11 54  16
KIMs d x y  SOMERs d x y
n   n  
(n   n    n  )
1154
= -0.5244
11  54  17
n   n  
n   n    n   n 
11  54
=-0.4388
11  54  16  17
WILSONs e  DEUCHLERs r
Die Häufigkeiten n<<, n<>, n>= usw. repräsentieren Werte der Kreuztabelle der ordinalen Paarvergleiche. n ist die Anzahl der UEen, I
bzw. J sind die Anzahl der x-Ausprägungen bzw. der y-Ausprägungen.
Bei allen Maßen ist im Zähler die Differenz zwischen der Anzahl konkordanter und diskordanter Vergleiche zu
finden, nur die Zähler sind verschieden. Vorwiegend die unterschiedliche Behandlung der Ties führen zu
verschiedenen Maßen. Vor allem KENDALLs a wird immer sehr klein, wenn Ties vorhanden sind.
Die Zusammenhangsmaße variieren zwischen –1 und +1. Ein negatives Maß signalisiert, dass für die Prädiktion
eher eine Diskordanzregel verwendet werden sollte.
4.8.2.3
Prädiktionsregeln und Fehlermaße
Die Zusammenhangsmaße können besser interpretiert werden, wenn sie in das Schema von PRE-Maßen
eingepasst werden. Diesen Versuch haben unter anderen Autoren HILDENBRANDT, ROSENTHAL u. LAING (1975)
Nagl, Einführung in die Statistik
Seite 166
und KIM (1971) unternommen und fanden, dass die meisten ordinalen Zusammenhangsmaße im Sinne von PREMaßen interpretierbar sind.
Hier soll für einige ordinale Zusammenhangsmaße die PRE-Interpretation vorgeführt werden. Da die
Prädiktionsregeln meist a-priori gesetzt werden, bietet sich vornehmlich die Interpretation der Maße als kappa
für bestimmte Regeln unter bestimmten Randbedingungen an.
GOODMAN-KRUSKALs 
Es wird unterstellt, dass entweder
Kreuztabelle der ordinalen
keine Ties vorhanden sind bzw. die Paarvergleiche ohne Ties:
Ties aus den
y
Prädiktionsüberlegungen
<
>
ausgeschlossen werden. Daher wird
x < c=n<<
d=n<>
nur ein Teil der
> d=n><
c=n>>
Paarvergleichskreuztabelle
c+d
c+d
Summe
betrachtet.
Als a-priori-Prädiktionsregel wird
die Konkordanzaussage
verwendet
Die Fehlerzellen sind die Zellen,
die der Prädiktionsaussage
widersprechen.
Als Fehler MIT wird der
gemeinsame Anteil in den
Fehlerzellen definiert.
Beispiel (Fortsetzung): Kreuztabelle der
ordinalen Vergleiche ohne Ties
y
Summe
<
>
<
>
11
54
54
11
Summe
65
65
Summe
65
65
130
x
c+d
c+d
2(c+d)
y
Für die Prädiktionsaussage
<
xi > xj  yi <> yj
x
<
>
sind die Fehlerzellen die ‚diskordant’Zellen in der Kreuztabelle.
Die Fehlerzellen sind die Zellen, die
als diskordant bezeichnet werden.
Fehler OHNE für kappa-Maße und PRE-Maß
Anteile unter Unabhängigkeit
Zur Berechnung des Fehlers
(OHNE) sind die gemeinsamen
y
Randanteil
<
>
Anteile unter Unabhängigkeit
0.25
0.25
0.5
x <
(fiktive Anteile) in den
0.25
0.25
0.5
>
Fehlerzellen erforderlich (oder die
0.5
0.5
1
Randant.
unter Unabhängigkeit erwartete
Anzahl)
Als Fehler OHNE wird als
F(OHNE)=0.25 + 0.25 = 0.50
Summe der fiktiven Anteile in den
Fehlerzellen definiert.
Das PRE-Maß ist die anteilige
PRE =1- (d/(c+d))/0.50= 1- 2d/(c+d)=
Reduktion des Fehlers durch die
= c  d  2d = c  d
Prädiktionsaussage= 1- F(M)/F(O)
cd
cd
= GOODMAN-KRUSKALs 
Ein negatives PRE (=GK)
Bei negativem  liefert der Betrag von
bedeutet, dass die
 die anteilige Reduktion des Fehlers
Diskordanzaussage zu bevorzugen durch die Diskordanzaussage
ist.
>
11
54
54
11
y
x
Fehleranteil(MIT)= 2d/(2 (c+d)) =
d/(c+d)= F(MIT)
<
<
>
<
>
11
54
54
11
Markiert
sind die
Zellen der
Prädiktionsaussage
Markiert
sind die
Fehlerzellen
Fehleranteil(MIT)=54/65=0.831= F(MIT)
y
<
>
Randanteil
<
>
0.5*0.5
0.5*0.5
65/130
0.5*0.5
0.5*0.5
65/130
Randant.
65/130
65/130
1
x
Die Summe in den Fehlerzellen über die
fiktiven Anteile (Anteile unter
Unabhängigkeit) = 0.5.
PRE=
c  d = 11  54 = -0.6612 ist
c  d 11  54
genau GK; hier aber abgeleitet als kappaPRE-Maß der Konkordanzaussage. D.h.
durch die Konkordanzaussage wird der Fehler
um 66.12% größer als bei Zufallszuordnung
werden
Die Diskordanzaussage reduziert den Fehler
um 66.12%
Entsprechende Überlegungen zur Interpretation sind ebenfalls für KENDALLs a möglich, sie sind aber nur dann
richtig, wenn wirklich keine Ties vorhanden sind.
SOMERs dxy
Die Ties werden bei der Prädiktionsinterpretation dieses Maßes nicht vollständig ausgeblendet. Die Prädiktions<
<
aussage ist ebenfalls die Konkordanzaussage ( xi > xj  yi > yj ).
Die verschiedenen möglichen Fehler werden aber unterschiedlich gewichtet.
Nagl, Einführung in die Statistik
Seite 167
Falls bei x ‚<’ der y-Wert ‚=’ (statt des prädizierten ‚<’) ist, wird der
Fehler nur halb gewichtet. Entsprechend bei x ‚>’.
Zu den Fehlergewichte bei x ‚=’ gibt es zwei mögliche Begründungen, die
zum gleichen Ergebnis führen:
a) Prädiktionen werden in dieser Situation nicht durchgeführt, daher 0 als
Fehlergewichte.
b) Sie werden zwar durchgeführt, Fehlprädiktionen aber nicht ‚bestraft’
-Fehlergewichte:
F(MIT x): gewichteter Fehleranteil
MIT Prädiktionsaussage.
Beispiel (Fortsetzung)
Damit die Formel bündiger
geschrieben werden können, sollen
die Anzahl der Paarvergleiche
durch c, d, a, b, e im folgenden
abgekürzt werden.
Jede Anzahl durch Gesamtvergleichsanzahl
g (Resultat: gemeinsame Anteile)
<
x =
>
Summe
<
c
b
d
y
=
a
e
a
k=
b+c+d
m=
e+2a
>
d
b
c
<
=
>
0
½
1
0
0
0
1
½
0
<
y
=
>
<
=
>
11
17
54
16
14
16
54
17
11
Summe
81
48
81
Summe
82
46
82
210
Summe
h=c+d+a
f= 2b+e
x
h=c+d+a
F (MIT)= (a*1/2+ d +
d
+ a*1/2)/g=
(2*d+a)/g
Fehler(MIT)= (16*1/2+ 54 +
54 + 16*1/2)/210=
(2*54+16)/210 =
=124/210
Fiktive Häufigkeiten:
Summe
h=c+d+a
x
f= 2b+e
h=c+d+a
PRE= (F(O)-F(M))/F(O)
= ((c+d+a) -(2*d+a) )/ c+d+a
= (c – d) / ( c+d+a)
in ursprünglicher Bezeichnung
<
=
>
Summe
g=e+
2(c+d+a+b)
F(OHNE): gewichtete Summe der F(OHNE)= (2*k*h/g + m*h/g) / g =
fiktiven Anteile (unter
(h(2k+m)/g) /g = (weil gilt: 2k+m=g)
Unabhängigkeit).
h /g = (c+a+d)/g
SOMERs dxy
y
<
x =
>
k=
g=e+
b+c+d 2(c+d+a+b)
Fehler OHNE.
Für die Berechnung des OHNEFiktive Häufigkeiten:
Fehlers werden die fiktiven Anteile
y
(unter Unabhängigkeit) benötigt.
<
=
>
Die fiktiven Anteile können aus
< k h/g m h /g k h/g
den fiktiven Häufigkeit berechnet
x = k f /g m f /g k f /g
werden durch Division durch die
> k h /g m h /g k h /g
Gesamtanzahl (=g). Die fiktiven
k=
m=
k=
Summe
Häufigkeiten sind die Produkte aus
b+c+d e+2a b+c+d
den Randhäufigkeiten durch
Gesamtanzahl.
Die Prozentuale Reduktion (PRE)
in dieser Interpretation ergibt:

z.B.
<
y
=
>
31.6
18.7
31.6
17.7
10.5
17.7
31.6
18.7
31.6
Summe
81
48
81
82
46
82
210
31.6 = 81*82 / 210
F(OHNE)= (2*82*81/210 + 46*81/210) /
210 (Anteilsbildung =diese zweite Division
durch 210)
= (81 (164 + 46) / 210) /210
81 /210 = (c+a+d)/g
PRE= (F(O)-F(M))/F(O) =
= (81 /210 - 124 /210) / (81 /210)
= -0.5309
=(11-54)/(11+54+16) = -0.5309
= (n<<-n<>)/(n<<+n<>+ n<=)
Entsprechend läuft die Interpretation von SOMERs dyx; dabei ist die Prädiktionsrichtung die von y nach x. Das
symmetrische dxy betrachtet als Szenario die Hintereinanderschaltung beider Richtungen.
KIMs dyx
KIM(1971) betrachtet folgende modifizierte Konkordanzaussage, die auch die Gleich-Bedingung mit einschließt
und bei der Konsequenz kleiner gleich bzw. größer gleich vorsieht:
<

>

yi = yj  xi = xj
Diese Prädiktionsaussage führte KIM zu folgenden Fehlergewichten:
Wird bei der y-Bedingung ‘<’ als x ‘’ prognostiziert, ist nur ‘>’ eine
Fehlprognose (mit Gewicht 1).
Wird bei der y-Bedingung ‘>’ als x ‘’ prognostiziert, ist nur ‘<’ eine
Fehlprognose (mit Gewicht 1).
Bei der y-Bedingung ‘=’ als x ‘=’ prognostiziert, ist ‘>’ oder auch ‘<’ eine
Fehlprognose (mit Gewicht ½).

<
x =
>
y
<
=
>
0
½
1
0
0
0
1
½
0
Diese Gewichte-Überlegungen begründen die gleiche Fehlergewichtematrix wie die, die zu SOMERs dxy geführt
haben. Daher sind beide Maße identisch.
Nagl, Einführung in die Statistik
Seite 168
4.9 Prädiktion und Kausalität
Wir haben bisher viele Formen des Zusammenhangs zweier Merkmale kennengelernt. Unter ‚Zusammenhang‘
kann sehr Verschiedenes gemeint sein. Hier sollen zwei wichtige Aspekte der Beziehung zwischen Merkmalen
herausgegriffen werden:
- KAUSALEr Aspekt: Ein Merkmal ‚beeinflusst‘ das andere (‚verursacht‘, ‚bewirkt‘ usw.)
- PRAEDIKTIVEr Aspekt: Die Kenntnis des einen Merkmals ermöglicht, die Ausprägung des andern zu
erschließen, oder zumindest die Chance für das Erschließen zu erhöhen.
In vielen Formulierungen der Umgangssprache sind beide Aspekte einer Beziehung undifferenziert gemeinsam
enthalten. Das kann zu Missverständnissen führen, zumal bei fast allen Konzepten der Beziehung zweier
Merkmale im Rahmen mengentheoretischer und logischer Betrachtungen nur der prädiktive Aspekt
berücksichtigt wird.
4.9.1 Prädiktive Beziehung zweier Merkmale
Prädiktion als Möglichkeit, die Werte eines Merkmals im Einzelfall mit Hilfe einer Regel richtig zuzuordnen,
wurde bereits eingeführt. Die Güte der Regel wird mit Hilfe von Fehlermaßen beurteilt.
Die zweidimensionalen Verteilungen zeigen, inwiefern
es möglich ist, aus der Kenntnis der x-Ausprägung die
y-Ausprägung im Einzelfall zu erschließen. Wenn
bestimmte Zellen exakt 0 sind (sei es aus logischdefinitorischen oder faktischen Gründen) kann eine
Regel für das Schließen bestimmter Ausprägungen des
einen Merkmals auf bestimmte Ausprägungen des
andern Merkmals erstellt werden, die in keinem
Einzelfall zu Fehldiagnosen führt. Eine solche
Beziehung zwischen x und y ( bzw. zwischen bestimmten
Ausprägungen von x und bestimmten Ausprägungen von y) sei als
deterministisch-prädiktive Beziehung zwischen x
und y (bzw. zwischen bestimmten Ausprägungen von x und
bestimmten Ausprägungen von y).
Mensch
Beispiele:
ja
nein
Die Tabelle erlaubt folgende Schlußre- Säugeja
>0
>0
geln: Falls eine UE ein Mensch ist, ist
tier
nein
0
>0
sie ein Säugetier (m  s).
Umgekehrt auch: Falls UE kein Säugetier ist, ist sie kein Mensch (s
 m). Diese Regeln führen ausnahmslos zu fehlerlosen Diagnosen.
Barometer steigt
ja
nein
Die Tabelle erlaubt folgende Schlußre- Wetter
ja
>0
0
wird
geln: Falls Barometer steigt, wird das
nein
0
>0
Wetter besser (bs  wb). Zudem noch: besser
Falls Barometer nicht steigt, wird das
Wetter nicht besser (bs  wb). Ebenfalls kann umgekehrt aus der
Wetterveränderung auf das Steigen des Barometers geschlossen
werden.
In vielen Bereichen wissenschaftlicher Forschung (Quantentheorie, Biologie, Sozial- und
Wirtschaftswissenschaften) sind deterministisch-prädiktive Beziehungen zwischen Merkmalen sogar eher die
Ausnahme.
Trotzdem können ‚Tendenzen‘ festgestellt werden und Beispiel: Prädiktion der Anteile, real
Angst vor
darauf aufbauend Prädiktionsregeln entwickelt werden, ‚Angst vor neuen
neuen Aufgaben
Aufgeben’ auf Grund
ja
nein
die zwar fehlerhaft sind, aber immerhin Rechenschaft
der Schulausbildung des
0.50
0.50
VS
0.50
über die Fehler geben und dadurch die Güte der Regeln Vaters (Volksschule vs. Vater
0.25
0.75
Ausbildung
HS+
0.50
Höhere
beurteilen. Solche Prädiktionsregeln können die Form
0.375
0.625
Schulausbildung).
logischer Aussagen annehmen (oder auch
Zumindest eine Tendenz ist hier vorhanden für die Aussage: höhere
Mittelwertsprädiktionsregeln, Regressionsregeln usw.) Schulausbildung reduziert die Angst des Kindes vor neuen Aufgaben.
In einer speziellen Situation, die als stochastische
Unabhängigkeit zwischen zwei Merkmalen
beschrieben wird, kann keine Prädiktionsregel
gefunden werden, die die Chance einer Verbesserung
der Prädiktion bei Kenntnis der Werte des einen
Im Beispiel: Falls die
bedingten Anteile bei
beiden
Ausbildungsarten gleich
groß sind, wäre die
spezielle Situation der
stochastischen
Anteile, fiktiv
Angst vor
neuen Aufgaben
ja
nein
Vater
VS
Ausbildung HS+
0.375 0.625
0.375 0.625
0.375
0.625
0.50
0.50
Nagl, Einführung in die Statistik
Merkmals für die Prädiktion einer Ausprägung des
anderen Merkmals erhöhen kann.
Seite 169
Unabhängigkeit gegeben. So wäre die Kenntnis der Vaterausbildung
nicht informativ für die Prädiktion der Angst
Solange aber die Merkmale abhängig sind, kann auch irgendeine eine Regel gefunden werden, bei der die Kenntnis des einen Merkmals die Chance einer Fehlerreduktion für der Diagnose des anderen Merkmals erhöht.
Eine stochastisch-prädiktive Beziehung zwischen zwei Merkmalen liegt genau dann vor, wenn die beiden
Merkmale stochastisch abhängig sind. Dann sind entweder die y-Verteilungen bei verschieden x-Ausprägungen
zumindest in Teilaspekten unterschiedlich (bei der Behandlung der Unabhängigkeit wurde gezeigt, dass dann
auch die x-Verteilung verschiedenen y-Ausprägungen verschieden sein müssen). Da die deterministischprädiktive Beziehung als Spezialfall einer stochastisch-prädiktiven dargestellt werden kann, wird in der Folge
nur von prädiktiver Beziehung gesprochen, daher:
Eine Beziehung zwischen x und y heiße prädiktiv, wenn die beiden Merkmale stochastisch abhängig sind.
4.9.2 Kausale Beziehung zweier Merkmale
‚Inhaltlich arbeitende Wissenschaftler finden oft Ursachen für die Phänomene, die sie untersuchen, ohne zu berücksichtigen, dass die
Wissenschaftstheoretiker den Begriff noch nicht hinreichend geklärt haben‘ (nach E. NAGEL, 1965).
Mit dem Begriff der Ursache sind sehr verschiedenartige Bedeutungen verbunden. Es wurde schon
vorgeschlagen, ihn für wissenschaftliche Zwecke überhaupt aufzugeben (RUSSEL, 1914); andererseits ist die
'Idee' von Kausalität in vielen wissenschaftlichen Konzepten indirekt und auch in Formulierungen der
Umgangssprache enthalten (siehe dazu z.B.: NAGEL(1966), SUPPES(1970), RUBIN(1978) und SKYRMS(1980)).
Mit ‚Ursache‘ ist mehr gemeint als nur eine Bedingung, die es erlaubt, auf die ‚Wirkung‘ zu schließen bzw.
umgekehrt.
z.B.: Zwar kann man unter einigen Zusatzvoraussetzungen aus der Tatsache, dass viele Leute den Regenschirm aufspannen, darauf
schließen, dass es regnet (bzw. umgekehrt); trotzdem ist das Schirmaufspannen niemals die Ursache für das Regnen.
z.B.: Auch beim Beispiel: Ausbildung des Vaters und Angst des Sohnes kann in beide Richtungen eine prädiktive Beziehung festgestellt
werden. Als Ursache für die Ausbildung des Vaters kommt aber die Angst des Sohnes kaum in Frage.
Damit soll aber nicht ausgeschlossen werden, dass im Rahmen einer Sequenz von Abläufen ein und dasselbe
Merkmal Ursache und Wirkung sein kann. Einige weitere bekannte, reale Beispiele aus der Forschung zeigen
sogar, dass trotz starker prädiktiver Abhängigkeit keines der beiden Merkmale die Ursache des andern sein
muss:
z.B.: Je größer die Storchendichte in einem Gebiet, desto höher die Geburtenrate.
z.B.: Je mehr Kirchen in einem Gebiet, desto mehr Diebstahlsdelikte gibt es dort.
z.B.: Mit steigender Lehreranzahl nimmt der Alkoholkonsum zu (die Lehrer sind wohl nicht Ursache des Alkoholkonsums).
z.B.: Je größer die Anzahl der Feuerwehrleute bei einem Brand, desto höher der Brandschaden. (Sind daher die Feuerwehrleute die
Brandschadenverursacher? Sollte daher die Zahl der Feuerwehrleute bei einem Brand eingeschränkt werden?)
Dieser Typ von Zusammenhang, bei dem eine dritte Variable für Zusammenhang verantwortlich ist, wird auch
als ‚Scheinkorrelation‘ bezeichnet (adäquater wäre wohl die Bezeichnung: ‚Scheinkausalität‘; denn die
Korrelation ist ja vorhanden).
Aus diesen Beispielen folgt:
Aus dem Vorliegen einer prädiktiven Beziehung folgt NICHT zwingend das Vorliegen einer kausalen.
Mit 'ein Merkmal ist Ursache für ein anderes' ist eher gemeint: Die Veränderung des ‚ursächlichen‘ Merkmals
löst (ohne weiteres Zutun) nach einer gewissen Reaktionszeit eine Veränderung im andern aus. Oft wird daher
(zusätzlich zur Existenz einer prädiktiven Beziehung) verlangt, dass die Ursache zeitlich vor der Wirkung
liegen muss (das trifft auch auf das Ausbildungs-Angstbeispiel zu).
Doch auch diese Forderung (zusätzlich zur Prädiktion) reicht nicht aus, Kausalität zu definieren, wie etwa das
Barometerbeispiel zeigt: steigt das Barometer, ändert sich die künftige Wetterlage; trotzdem ist die Höhe des Barometerstandes selbst
nicht die Ursache für die spätere Wetterlage.
Zu meinen, weil immer ein Ereignis B nach einem Ereignis A auftrete, müsse A die Ursache von B sein, wäre
daher falsch ( das ist der ‚post hoc, ergo propter hoc' -fehlschluss).
Weiters wird für das Vorliegen einer kausalen Beziehung meist eine raum-zeitliche Nähe von Ursache und
Wirkung verlangt; allerdings gibt es keine exakten Kriterien, was damit genau gemeint ist (siehe E. NAGEL,
1966).
Nagl, Einführung in die Statistik
Seite 170
Während bei der 'klassischen' Formulierung der Kausalität, die im wesentlichen von G. GALILEO, D. HUME und
J. S. MILL geprägt wurde, die Relation zwischen dem ursächlichen Merkmal und dem bewirkten Merkmal
deterministisch exakt sein muss (oder anders ausgedrückt: das Fehlermaß für die Prädiktion des bewirkten
Merkmals muss bei Berücksichtigung von x null sein), begnügen sich heute viele Wissenschafter mit einer
stochastischen Relation (z.B.: LAZARSFELD(1955), GALTUNG(1965), WOLD(1966), SUPPES(1975),
RUBIN(1978), SKYRMS(1980)).
4.9.2.1 Stimulus-Response-Definition der Kausalität von WOLD
Die folgende Definition wurde von H. O. A. WOLD(1966) vorgeschlagen und wird hier leicht modifiziert
wiedergegeben. Sie erfüllt die Forderung nach raum-zeitlicher Nähe (zw. Ursache und Wirkung), nach der
zeitlichen Priorität der Ursache und lässt eine stochastische Relation zwischen dem ursächlichen und dem
bewirkten Merkmal zu.
Zudem stellt sie nicht nur eine Begriffsklärung dar, sie zeigt konstruktiv, wie überprüft werden kann, ob eine
kausale Relation vorliegt. Sie orientiert sich am Experiment im engeren Sinn und kann als S-R-Kausalität
bezeichnet werden (Stimulus-Response). Da sie auf nichtexperimentelle ebenso wie auf experimentelle
Untersuchungssituationen anwendbar sein soll, werden zwei Fälle unterschieden. Sie beginnt mit der
Charakterisierung des Experiments im engeren Sinn.
Bei einem EXPERIMENT im engeren Sinn sind drei Gruppen
von Variablen vorhanden:
1.
2.
3.
Die Stimulusvariablen sind die Variablen, deren
Ausprägungen vom Untersucher systematisch variiert
werden,
Die Responsevariablen sind die Variablen, die nur beobachtet
werden,
Die ‚Stör-Größen‘, die im Exp. je nach Art der Variablen
unterschiedlich behandelt werden:
a) Zufallsstörgrößen: Variablen, von denen auf Grund
theoretischen Wissens angenommen werden kann, dass
sie keinen systematischen Einfluss auf den Response
haben,
b) Systematische Störgrößen: Variablen, von denen ein
systematischer Einfluss erwartet wird und daher:
b1) konstant gehalten werden oder,
b2) deren Einfluss mit Hilfe von Zufallsvariation
(Randomisierung) neutralisiert wird.
Beispiel: Durchführung eines Experiments im engeren
Sinn zur Überprüfung der Frage, ob Studenten Statistik
besser lernen können, wenn ihnen ein Skript vorliegt.
Stimulusvariable: Lehrmittel Skript (ja/nein); einige
Studenten bekommen ein Skript, andere nicht.
Responsevariable: Ergebnis der Klausur (in
Leistungspunkten).
Störvariablen:
a) wohl irrelevant: Körpergröße, Augenfarbe usw.
b) eventuell relevant: Intelligenz, Lesefähigkeit,
Motivation.
b1) Konstanthalten: z.B. nur diejenigen vergleichen, die
gleich intelligent (motiviert etc.) sind usw.
b2) damit die beiden Gruppen ungefähr gleich
zusammengesetzt sind, sollte per Zufall (z.B.
Münzwurf, Kugeln aus Urne ziehen) festgelegt werden,
wer ein Skript bekommt und wer nicht (das wäre eine
Form von Randomisierung und würde mit hoher
Wahrscheinlichkeit unerwünschte Störeffekte
verhindern, wie z.B. dass sich die freiwillig für die
Skriptgruppe melden (etwa hochmotivierte), die auch
ohne Skript gute Leistungen brächten, usw.)
Die Ausprägungen der Stimulusvariablen werden auch als Stimuli oder Behandlungen (engl. Treatments)
bezeichnet; es sind wohldefinierte Aktionen des Experimentators.
S-R-Definition
Fall I (die Untersuchung ist ein Experiment im engeren Sinn):
Sind bei den unterschiedlichen Stimuli unterschiedliche
Verteilungen der Responsevariablen feststellbar, liegt eine
KAUSALE Beziehung vor. Die Stimulus-Variablen werden als
URSACHEN, die Response-Variablen als WIRKUNGEN
bezeichnet.
Fall II (es liegt KEIN Experiment vor; Gedankenexperiment):
Falls kein Experiment im engeren .Sinn durchgeführt wurde oder
bei der gegebenen Problemstellung nicht durchführbar ist, soll
ein solches Experiment GEDANKLICH durchexerziert werden
unter Verwendung allen bis dato verfügbaren Wissens und auf
diese Art entschieden werden, ob bzw. in welchem Ausmaß eine
fragliche Variable (als Stimulus fungierend) bei systematischer
Variation ‚automatisch‘ Unterschiede in der Verteilung des (als
Response-Variable betrachteten) Merkmals nach sich zieht.
Nach Durchführung des Experiments würden die beiden (Mit/Ohne Skript) Verteilungen der
Leistungsergebnisse verglichen.
Ergäben sich Unterschiede (bzw. gravierende
Unterschiede), könnte man sagen, dass die
Skriptausgabe die Leistung beeinflusst.
Beispiel: Bei ‚Vater-Ausbildung und Angst’ seien
Verteilungsunterschiede gesichert festgestellt.
Die Untersuchung ist kein kontrolliertes Experiment.
Das Experiment wird gedanklich durchgeführt. Was ist
Ursache?
Sei Ausbildung des Vaters Stimulusvariable; kann das
zu Unterschieden in der Angst der Kinder (als
Responsevariable) führen?
Bzw. umgekehrt: Ist es vorstellbar, dass bei Angst der
Kinder als Stimulusvariable die Verteilung der
Väterausbildung (bei Angst ja) verschieden ist vom
Nagl, Einführung in die Statistik
Seite 171
Treatment(Angst nein) verschieden wären, falls ein
solches Experiment durchgeführt würde?
Statt nur zu fordern, dass zwischen den verschiedenen Verteilungen Unterschiede vorhanden sein müssen,
könnte auch gefordert werden, dass die Unterschiede ein bestimmtes Ausmaß überschreiten sollen, wenn von
kausaler Beziehung gesprochen werden soll.
Aus der Definition folgt für das Verhältnis zwischen kausaler und prädiktiver Beziehung (abgesehen von der
Gesamtheit-Stichproben-Problematik): Falls Merkmal x Ursache für ein Merkmal y ist, so sind bei
unterschiedlichen Ausprägungen von x die bedingten Verteilungen unterschiedlich (d.h. stochastische
Abhängigkeit, daher auch eine prädiktive Beziehung); kurz:
Falls eine Beziehung zwischen x und y kausal ist, ist sie auch prädiktiv.
4.9.2.2 RUBINs Konzeption der Kausalität als virtueller Unterschied
Sehr grundlegend ist die Konzeption, die D. B. RUBIN in einer Reihe von Artikeln entwickelt hat (1974, 1977,
1978, 1980) und von P. W. HOLLAND(1986) im Vergleich mit anderen Konzeptionen dargestellt wurde. In der
nachfolgenden Darstellung sollen nur zwei Stimuli (spezielle Behandlung versus ‚Vergleichs’-Behandlung)
betrachtet werden.
Eine Vergleichsbehandlung könnte auch eine Nicht- oder Kontroll-Behandlung sein; es soll grundsätzlich beachtet werden, dass auch eine
Kontroll-Behandlung prinzipiell eine Behandlung darstellt.
Die zentrale Idee dabei ist, dass die Auswirkung einer bestimmten Behandlung nur dann eindeutig festgestellt
werden könnte, wenn die UE zur gleichen Zeit sowohl behandelt als auch nicht behandelt würde. Der Response-Unterschied zwischen diesen beiden Zuständen (behandelt und nicht behandelt) wird als die Auswirkung
der Behandlung angesehen; dieser Unterschied ist wird als der kausale Effekt der Behandlung bezeichnet. Allgemeiner kann von einem Vergleich zweier Behandlungen (Behandlung und Vergleichsbehandlung) gesprochen
werden.
Die Differenz in der
Responsevariablen zwischen
behandeltem und vergleichsbehandeltem Zustand wird als der
kausale Effekt der Behandlung
(relativ zur Vergleichsbehandlung)
für eine Untersuchungseinheit
definiert
D bv (u ) := Yb (u)  Yv (u) Die Differenz D bv (u ) im Response Y für UE
(=u) zwischen Behandlung(=b) und
Vergleichsbehandlung(=v) ist der
kausale Effekt von b auf u bezüglich
der Responsevariablen Y im Vergleich
zur Behandlung v.
Beispiel(Skriptbeispiel): Das
Prüfungsergebnis (=Response) für Herrn
Franz im WS 2000 (=u) sei 80 Punkte, falls
er ein Skript (=Behandlung b) erhält; wenn er
keines erhält (=v) erzielte er nur 60 Punkte.
Daher ist der kausale Effekt des Skripts
gegenüber ohne Skript für Herrn Franz im
WS 2000 bezüglich des Prüfungsergebnisses
Y: Dbv(u):= 80 – 60 =20; mit Yb(u)=80 und
Yn(u)=60
Statt der Differenz könnte grundsätzlich auch eine andere Vergleichsoperation für den Response beider Behandlungen verwendet werden.
Die kausalen Effekte
(Unterschiede) müssen
für die verschiedenen
UEen der Population
nicht alle gleich sein.
Dann kann die Verteilung der kausalen Effekte erstellt werden.
Eventuell wird nur ein
bestimmter Parameter
dieser Verteilung (z.B.
der Mittelwert) betrachtet.
100
Yv
Differenzen
Yb
90
50
80
40
70
30
60
20
50
10
40
0
30
20
10
0
v
b
Virtuelle Positionen
Der durchschnittliche kausale
Effekt der Behandlung für die
Population der UEen kann als
Erwartungswert der Differenz geschrieben werden
b-v
Verteilungsdiagramm:
Jeder kleine Punkt
repräsentiert die Differenz einer Person
 = E( D bv )=E( Yb  Yv ) =
(da der Erwartungswert der Differenz gleich der
Differenz der Erwartungswerte ist) =
E(Yb )  E(Yv ) =  b   v
Beispiel(Skriptbeispiel): Der
Übersichtlichkeit halber bestehe die
Population, aus der Herr Franz im WS 2000
gezogen wurde, nur aus 10 Personen.
Für jede der 10 Personen wurden im
Diagramm ganz links jeweils beide
Ergebnisse als kleine Punkte eingetragen (das
hypothetische Ergebnis mit Skript (=b) und
das hypothetische Ergebnis ohne Skript (=v))
und jeweils mit einer Linie verbunden.
Für jede Person wurden kausale Effekte
berechnet (Differenzen) berechnet und ein
Verteilungsdiagramm erstellt.
Die fetten Punkte stellen die jeweiligen
Mittelwerte dar.
Der über die Differenzen berechnete
Mittelwert ist = 25.
Der Mittelwert über die v-Werte ist 39 =v.
Der Mittelwert über die b-Werte ist 64 =b.
Daher auch:  = 25 = 64 – 39.
Nagl, Einführung in die Statistik
Seite 172
Das zentrale Problem ist aber, dass eine UE nicht zugleich beide Behandlung erhalten kann bzw. dass pro UE
nicht beide Arten von Responses beobachtet werden können: das ist das virtuelle an der Konzeption. HOLLAND
bezeichnet dieses Problem denn auch als das Fundamentalproblem des kausalen Schließens.
Die Konzeption erlaubt aber, die mit dem kausalen Schließen verbundenen Probleme besser zu veranschaulichen. Sie ist eine idealtypische Vorstellung, an der die Güte der praktizierten Lösungen des kausalen Schließproblems gemessenen werden können.
Die üblichen Lösungen des Problems liegen darin, Experimentalbedingungen zu realisieren, die der idealtypischen Situation sehr nahe kommen. Dabei sind Invarianzannahmen notwendig, die aus inhaltlich-theoretischen
Gründen gerechtfertigt werden sollten. Die Lösungen können in zwei Typen eingeteilt werden:, Messungen mit
verbundenen (Wiederholungs- bzw. ‚Zwillings’-Messungen) oder unverbundenen UEen (Gruppenmessungen).
4.9.2.2.1 Verbundene Messungen
Im wissenschaftlichen und alltäglichen Anwendungsbereich ist diese Form der Annäherung an die idealtypische
Situation die üblichste. Beide Behandlungsarten werden appliziert und gemessen, entweder zeitlich leicht verschoben oder an fast gleichen UEen.
Wiederholungsmessungen
Falls die Wirkung einer Behandlung keine bleibende Veränderung in der UE nach sich zieht, kann die gleiche
UE zeitlich verschoben beiden Behandlungen ausgesetzt und der Response jeweils wiederholt gemessen werden.
Annahmen: Die Anwendung
mindestens einer Behandlung ist
nur vorübergehend (kausal
transient), damit die andere
Behandlung auf eine quasi
unveränderte UE angewandt
werden kann; zudem sollte der
vorher gemessene Response
zeitlich stabil sein, damit der
Vergleich mit dem nachfolgenden
Behandlungsresponse so berechnet
werden kann, als ob die beiden
Behandlungen simultan
durchgeführt würden.
Spezialfall: Verlaufsmessung. Die
Vergleichsbehandlung sei die Nichtbehandlung. Der Y-Anfangszustand (oder auch zu
mehreren Zeitpunkten) werde gemessen (vor
der Behandlung). Ab einem bestimmten
Zeitpunkt beginnt die Behandlung b
(eventuell liegen auch mehrere Messungen
vor).
Die Bestimmung des kausalen Effekts erfordert auch hier Annahmen über den
Verlauf des Y-Zustands, der ohne Behandlung zu erwarten wäre. Je nach
angenommenem (bzw. begründet hochgerechnetem) Verlauf kann eine Behandlung
eventuell einen negativen oder positiven
Effekt haben.
Kausale Transienz: Die UE wird
durch Behandlung v nicht nachhaltig
verändert. Die nachfolgende Behandlung b würde das gleiche Responseergebnis erbringen, wenn es vor der
Behandlung v angewandt würde.
Zeitliche Stabilität: Wegen der
Forderung des zeitlich simultanen
Vergleichs muß das Responseergebnis
von v zeitlich konstant bleiben (oder
zumindest hochgerechnet werden können für den Zeitpunkt, zu dem b evaluiert wird).
b-Behandlung
b-Behandlung
100
100
Y
Y
+
50
50
0
0
100
100
Y
+
Y
50
0
-20
Beispiel (Knipsen eines Lichtschalters in
einem Raum u): Unter der Randbedingung,
dass die Leitung unter Strom steht, kann der
kausale Effekt des Anschaltens (Behandlung
b) mit dem des Ausschaltens (Behandlung v)
bezüglich des Lichteffekts (Response)
bestimmt werden.
Hier gilt wohl, dass die Behandlung v den
Raum u nicht nachhaltig verändert und der
kurze Zeitraum zwischen v und b wohl
irrelevant ist. Daher kann der ResponseUnterschied so beurteilt werden, als ob der
Schalter gleichzeitig an oder aus wäre.
-10
0
10
20
30
Zeit
50
+
0
-20
-10
0
10
20
30
Zeit
Beispiel: Zwei Verlaufsarten des YResponse über die
Zeit (Bilder oben
bzw. unten) sind
fett gezeichnet.
Die b-Behandlung
läuft ab Zeitpunkt 0.
Der ab Zeitpunkt 0
gedachte(extrapolierte) Verlauf ist
dünn gezeichnet.
Der kausale Effekt
von b wird nach Ende der Behandlung
festgestellt.
Paar-Messungen
Einer andere Art der Annäherung an den Idealzustand besteht dann, wenn Paare von UEen vorhanden sind, die
in ihrer Struktur gleichartig sind. Dann kann bei der einen UE der Response der einen Behandlung, bei der
anderen UE der der anderen Behandlung gemessen werden.
Nagl, Einführung in die Statistik
Seite 173
Beispiel (KöchIn untersucht zwei Varianten
des Zubereitens von Broccoli; 5 Minuten versus 7 Minuten Kochen): als UEen können
zwei verschiedene Broccolis (u1, u2)
verwendet werden. Hier ist es sicher möglich,
zwei völlig gleichartige Broccolis zu finden,
die unterschiedlich behandelt werden können.
Annahme: Gleichartigkeit der
beiden UEen (UE-Homogenität),
auf die die unterschiedlichen
Behandlungen angewandt werden
Homogenitätsannahme:
Yv (u 1 )  Yv (u 2 ) und
Spezialfall: Matching. Zu jeder UE,
Seien X1, X2, … , Xm Merkmale, die für die
Responsevariable Y relevant sind. Auf Grund
dieser Merkmale wird eine UE u2 aus einem
Pool von UEen gesucht, für die die Distanz von
u2 bezüglich der m X-Merkmale zu u1 minimal
ist.
Yb (u 1 )  Yb (u 2 )
für jedes Paar u 1 , u 2
die mit b behandelt werden soll, wird eine
UE gesucht,die in vielen für Y relevanten
Eigenschaften möglichst ähnliche Werte hat
und mit v behandelt wird.
Beispiel: Für den Therapieerfolg könnten
Alter, Geschlecht, Ausbildung,
Therapieerfahrung, Motivation usw. wichtig
sein. Für den Vergleich zweier Therapien soll
zu jedem Teilnehmer der einen Therapieform
ein bezüglich dieser Eigenschaften gleicher
für die andere Therapieform gesucht werden.
4.9.2.2.2 Unverbundene Messungen
In allen anderen Fällen (nachhaltige Veränderung der Untersuchungseinheiten durch eine Behandlung bzw.
Mangel an gleichartigen UEen) müssen die Responsewerte für die eine Behandlung an einer Gruppe von UEen,
die Responsewerte für die andere Behandlung an einer anderen Gruppe von UEen durchgeführt werden.
Unabhängigkeitsforderung
Jede UE muß nun alterna- 100
Yv
Yb
Yv
Yb
100
tiv entweder der Behand- Y 90
90
lung oder der Vergleichs80
80
behandlung zugeordnet
70
70
werden. Diese Selektion
60
60
führt dazu, dass für jede
50
50
UE nun nur die Response40
40
variable Y und die Grup30
30
penzugehörigkeit (=X)
20
20
vermerkt wird. Die Grup10
10
penzugehörigkeit
0
0
v
b
v
b
repräsentiert implizit die
X: Gruppe
X: Gruppe
Selektion des
entsprechenden Yv bzw.
Y b.
Für jede Gruppe kann die VerteiBezeichnung der Mittelwerte:
lung für die jeweils ausgewählten M. in Behandlungsgruppe= E(Yb| X=b)
Werte berechnet werden. Hier sol- M. in Vergleichsgruppe = E(Yv| X=v)
len nur die beiden Gruppenmittel- (bedingte Mittelwerte, oder
werte betrachtet werden.
Gruppen-Mittelwerte)
Bei dieser Selektion der
Responsewerte in die entsprechenden Gruppen
kann manches schief laufen, so daß völlig falsche
Vorstellungen über die
kausalen Effekte entstehen.
Der Grund liegt meist in
nicht adäquater
Zuordnung der UEen zu
den Gruppen
Überschätzen des Effekts
bei ‚Hochmotivierten’
100
90
80
80
70
70
60
60
50
50
40
40
30
30
20
20
10
10
v
b
X: Gruppe
Um den Bezug zu den virtuell
vollständigen Responsewertepaaren
herzustellen, wurden im linken Bild
zu den Punkten, die die Y-Messwerte repräsentieren, auch die Linien
zum fehlenden Paarwert dargestellt
(sie sind aber in der vorliegenden
Situation leider nicht mehr
vorhanden).
Im vorliegenden Beispiel sind die beiden
Mittel der selegierten Werte:
E(Yb | X=b) = 64 und E(Yv | X=v) = 39
Diese Mittelwerte stimmen hier
‚glücklicherweise’ exakt mit den obigen
Mittelwerte E(Yv) und E(Yb) überein.
Unterschätzen des Effekts
bei ‚Förderzwang’
100
90
0
Der Y-Messwert (hier die
Prüfungsergebnisse) jeder
Untersuchungseinheit ist nun
entweder der Yv- oder der Yb-Wert
und zwar je nachdem, ob die UE der
v- oder b-Gruppe zugeordnet wurde
(rechtes Bild).
0
v
b
X: Gruppe
Angenommen, das Skript wird jenen
Personen gegeben, die sich zuerst
melden. Dabei würden wohl die
hochmotivierten das Skript bekommen, die auch ohne Skript hohe Responsewerte hätten. Für die bGruppe sind daher besonders hohe
Responsewerte vorhanden (der
kausale Effekt würde überschätzt).
Im zweiten Fall bekommen nur diejenigen das Skript, die schlechte
Abiturnoten haben (sie sollen
gefördert werden!). Dadurch
werden besonders ihre niedrigen
Responsewerte für die Skriptgruppe
ausgewählt; Konsequenz: der
kausale Effekt wird unterschätzt)
Nagl, Einführung in die Statistik
Seite 174
Der auf Grund der Differenz der
Gruppen-Mittelwert berechnete
Unterschied wird als Prima-FacieKausaleffekt bezeichnet.
Die Gruppenunterschiede repräsentieren den kausalen Effekt
dann, wenn die Gruppen-Mittelwerte gleich den Mittelwerten
der virtuellen Werte sind. Das
stellt eine Unabhängigkeitsforderung dar: Die Selektion der Werte
in die Gruppen sollte keinen
Zusammenhang mit der Höhe der
Werte haben.
Der PF-Kausaleffekt ist die Differenz
der Gruppenmittelwerte:
D = E(Yb| X=b)- E(Yv| X=v)
Der PF-Kausaleffekt in den beiden Fällen:

Hochmotivierte: D = 75-28 = 47

Zwangsgeförderte: D = 53-50 = 3
Bei den Hochmotivierten in der Skriptgruppe
Die Gruppenmittelwerte liefern den
kausalen Effekt, wenn folgende Y-Un- sind die Gruppenmittelwerte:
E(Yb | X=b) = 75 und E(Yv | X=v) = 28
abhängigkeitsforderungen (hier für
die Mittelwerte formuliert) gelten:
Bei den Zwangsgeförderten in der
E(Yb)
E(Yv)
Skriptgruppe sind die Gruppenmittelwerte:
E(Yb | X=b) = 53 und E(Yv | X=v) = 50
= E(Yb| X=b)
= E(Yv| X=v)
Diese Gruppenmittelwerte stimmen nicht mit
den Mittelwerten E(Yv) bzw. E(Yb) überein;
daher ist die Unabhängigkeitsforderung
verletzt.
D.h. die Mittelwerte über die virtuellen
Werte sollen gleich groß sein wie die
Gruppenmittelwerte
Etwas anders formuliert: Keine UE sollte weDie Y-Unabhängigkeitsforderung Die Verteilung aller Yb –Werte soll
gen des zu erwartenden ‚Erfolgs’ oder
kann auf die Verteilung der Werte gleich der Verteilung in Gruppe X=b
‚Misserfolgs’ einer der beiden Gruppen
ausgedehnt werden.
sein; analog für X=v.
zugeordnet werden (auch nicht implizit)!
Wenn die Unabhängigkeitsforderung erfüllt ist, ist der PF-Kausaleffekt gleich dem Kausaleffekt.
Konstanthaltung
Die Unabhängigkeitsforderung ist nicht direkt mess- und überprüfbar, da sie sich auf die virtuellen Y-Werte
bezieht. Überprüfbar ist hingegen eine andere Implikation der virtuellen Konzeption: die Unabhängigkeit der
Gruppenvariablen von möglichen ‚Drittvariablen’. Da nach der virtuellen Konzeption Yv und Yb an den gleichen
UEen gemessen werden, sind die Verteilungen für alle denkbaren Merkmale (außer für Y selbst) gleich. Die
Selektion in die beiden Gruppen sollte so erfolgen, daß die Verteilungen dieser Merkmale in den beiden Gruppen
möglichst ähnlich sind (‚Drittvariablen’ sind somit alle möglichen Merkmale außer der Y- und der Gruppenvariablen); anders formuliert: keine Drittvariable sollte mit der Gruppenvariable prädiktiv zusammenhängen bzw.
keine Drittvariable sollte mit der Gruppenvariablen korrelieren.
Falls eine bestimmte Drittvariable Z mit der Gruppenvariablen korreliert, sollen die Gruppenunterschiede
unter Konstanthaltung von Variable Z berechnet werden.
Hier korreliert die
Eine wichtige KonstanthalDarstellung der individuellen Werte Hochmotivierter (Dreicke) und Gruppeneinteilung mit Motivation
tungsstrategie besteht dar(in v ist das Verhältnis von
Niedrigmotivierter(Kreise) bzw. der Mittelwerte
in, die UEen nach den
Hochmotivierten zu
Mittelwertprofile,
Ausprägungen von Z in
Niedrigmotivierten 4:1, in b
Y
Y
v
b
100
100
nach Motivation
hingegen 1:4). Die Unterschiede
Strata (Schichten, Gruppen
stratifiziert
90
90
sind hier durch die Größe der
nach Z) einzuteilen und
Mittelwertsymbole repräsentiert.
80
80
innerhalb jedes Stratums
70
70
die Gruppen bezüglich Y
Werden die Mittelwerte getrennt
60
60
für jede der beiden
verglichen (diese Strategie
50
50
Motivationsniveaus verglichen,
kann als Stratifikations40
40
entsteht eine realistische
konstanthaltung bezeichEinschätzung des
30
30
net werden)
Behandlungseffekts (dicke Linien
20
20
10
0
10
v
b
Virtuelle Positionen
Der Globalvergleich der
Gruppen verzerrt bei
Korrelation mit einer
Drittvariable das Ergebnis.
0
und ohne
Stratifikation
v
b
X: Gruppe
Ein globaler Vergleich (ohne Differenzierung nach Z)
der Gruppen(v, b) bezüglich Y würde wegen der disproportionalen Anteile der Strata (in den beiden Gruppen)
implizit die Strata in den Vergleich mit einbeziehen; das
würde aber den Vergleich der Gruppen verzerren.
in der rechten Graphik).
Würde der Gesamtmittelwert (in
der rechten Graphik bei der
dünnen Linie dargestellt) für v
und b verglichen, entstünde ein
inadäquater Eindruck.
Beim Gesamtmittelwertvergleich
würden schwerpunktmäßig vor
allem Hochmotivierte (aus v) mit
Niedrigmotivierten (aus b)
verglichen.
Voraussetzung für die Konstanthaltung ist aber, dass in jedem Stratum beide Arten der Gruppen repräsentiert
sind. Falls dies nicht der Fall ist, sind die geforderten stratifizierten Vergleiche nicht möglich (eine solche Konstellation wird als Konfundierung von Treatment- und Z-Variablen bezeichnet; bei vollständiger Konfundierung ist kein einziger Vergleich möglich, bei teilweiser Konfundierung sind nicht alle Vergleiche möglich ).
Nagl, Einführung in die Statistik
Seite 175
4.9.2.2.2.1 Experimentelle Untersuchungen: Randomisierung und Konstanthaltung
In Experimentellen Untersuchungen gilt die Randomisierung als die zentrale Strategie zur Lösung des Problems, die Unabhängigkeitsforderung zu erfüllen.
Die Randomisierung garantiert
aber nicht, daß in einem konkreten Experiment die Forderung erfüllt ist.
Die Verteilung der Ergebnisse, die
bei allen möglichen Randomisierungen erzielt werden können, zeigt
diese Situation.
Die UEen werden mit Hilfe eines Zufallssmechanismus der einen oder andern Behandlungsgruppe zugeordnet.
Skriptbeispiel (Fortsetzung): Durch Ziehen
eines Loses aus einer Urne mit 10 Zetteln (5
davon sind mit ‚Skript’ markiert) wird
bestimmt, wer von den 10 UEen in die
Skriptgruppe kommt.
Verteilung der möglichen
Ergebnisse bei Randomisierung
Skriptbeispiel(Fortsetzung): Bei 10 UEen
können 252 verschiedene Aufteilungen in
zwei 5er-Gruppen erzeugt werden. Eine
solche Aufteilung stellt ein Experiment dar,
mit einem PF-Kausaleffekt.
0.2
Anteil
Randomisierung erhöht die
Chance, dass die Unabhängigkeitsforderung erfüllt ist
0.15
0.1
0.05
0
-10 0
Für die oben dargestellte Population wurden
für alle 252 Experimente die Kausaleffektmittel berechnet. Die Graphik(links) zeigt die
Verteilung all dieser Ergebnisse.
10 20 30 40 50 60
PF-Kausaleffekt
Die Verteilung beschreibt die Chance für
bestimmte PF-Kausaleffekt
Als zusätzliche Vorsichtsmaßnahme sollte daher im konkreten Fall trotz
Randomisierung untersucht werden, ob die Gruppeneinteilung nicht doch
eine Zusammenhang mit einem Merkmal hat, das auch für die Responsehöhe relevant ist. Das Merkmal sollte dann konstantgehalten werden.
Allerdings erhöht (mit zunehmender Stichprobengröße) die Randomisierung auch die Chance, dass Drittvariablen mit der Gruppenvariablen in
keinem prädiktiven Zusammenhang stehen, da die Randomisieung
‚gegen jede Systematik wirkt’.
Im schlimmsten Fall ist der PF-Kausaleffekt
–8 bzw. 58, allerdings kommt das selten vor.
Skriptbeispiel: Auch bei Randomisierung
könnte eine Gruppeneinteilung ‚passieren’,
die etwa überwiegend die Hochmotivierten
der Skriptgruppe zuordnet.
Skriptbeispiel: Bei Randomisierung steigt bei
zunehmender Größe der Stichprobe die
Chance, dass die Skriptvariable mit keinem
Merkmal (Motivation, Intelligenz usw.)
prädiktiv zusammenhängt.
Diese Randomisierungs-Strategie kann verbessert werden durch stratifizierte Randomisierung. Sie stellt eine
Konstanthaltungsstrategie dar, die schon vorn vorherein bekannte Zusammenhänge berücksichtigt. Eine mögliche Konfundierung der Gruppenvariablen mit der Stratifizierungsvariablen kann dadurch verhindert werden.
Wenn von vornherein vermutet
werden kann, daß der Response
mit einem bestimmten Merkmal Z
zusammenhängt, sollte dieses
Merkmal schon bei der Auswahl
der UEen berücksichtigt werden.
Für jedes Stratum zi kann
kann der kausale Effekt
berechnet werden:
100
Bei der stratifizierten Randomisierung
werden die UEen vor der Auswahl auf
Grund der Ausprägungen (zi , i=1,...,I)
eines Merkmals Z in Gruppen (Strata
genannt, damit eine Verwechslung mit
der Bezeichnung ‚Gruppe’ bei Behandlungs- und Vergleichsgruppe vermieden wird) eingeteilt.
Yv
Yb
90
80
(Z=zi)
=
E(Yb -Yv| Z=zi) =
E(Yb | Z=zi) - E(Yv| Z=zi).
60
50
40
Dabei ist E(Yb | Z=zi) der
Mittelwert des
Behandlungsresponse für
das i. Stratum (auch
bedingter Mittelwert
genannt); entsprechend
E(Yv | Z=zi).
30
niedrig
hoch
Motivation
20
10
0
Differenzen
in den Motivationsgruppen
50
40
30
20
10
0
70
v
b
Virtuelle Positionen
Skriptbeispiel (Fortsetzung): Von vornherein
kann etwa die Motivation(=Z) als ein
wichtiges Merkmal angesehen werden, von
dem der Response (Klausurergebnis) stark
abhängen wird.
Daher sollten die UEen zuerst nach
Motivation in 2 Gruppen eingeteilt werden:
z1=n (niedrig) und z2=h (hoch)
Die UEen in der Population (und
damit auch die virtuellen
Responsewerte) werden nach den
Ausprägungen von Motivation
(niedrig, hoch) stratifiziert.
In jedem Stratum kann der
Mittelwert für Yv und Yb
berechnet werden:
E(Yv | Z=n)=28, E(Yb | Z=n)=53;
E(Yv | Z=h)=50, E(Yb | Z=h)=75;
Der kausale Effekt stimmt im vorVerteilung der Differenzen
liegenden Fall für beide Strata
(Yb -Yv) und deren Mittelwerte
überein:
(große Symbole, jeweils rechts)
 (Motivation=n) = 25= 53 – 28.
 (Motivation=h) = 25 = 75 – 50.
Nagl, Einführung in die Statistik
Innerhalb jedes Stratums
wird randomisiert
Für jede Gruppe in jedem
Stratum könnte die Verteilung berechnet werden.
Seite 176
Pro Stratum werden jeweils nach den Prinzipien der
Randomisierung die UEen wiederum exklusiv einer der
beiden Behandlungsgruppen zugeordnet.
100
Yv
Yb
90
80
Hier sollen die GruppenMittelwerte ausreichen im
i. Stratum:
50
40
30
20
10
0
70
60
50
40
30
10
(bedingte Gruppenmittel
mit den Bedingungen
Gruppe und Stratum)
0
Auf der Basis der bedingten
Gruppen-Mittelwerte kann der PFKausaleffekt für jedes Stratum
berechnet werden.
Die PF-Kausaleffekte werden bei
manchen Fragestellungen über die
Strata gemittelt werden.
Durch die stratifizierte Randomisierung können die kausalen
Effekte besser geschätzt werden.
Die Verteilung aller möglichen
Experimentalergebnisse wird
schmaler, die Extremfälle rücken
näher an den wahren kausalen
Effekt heran.
Die Unabhängigkeitsforderung
kann nun ersetzt werden durch
eine, die sich auf jedes Stratum
bezieht anders ausgedrückt: die
Ausprägungen von Z werden als
Bedingung eingefügt.
Die Gruppenunterschiede repräsentieren den kausalen Effekt
dann, wenn die Gruppen-Mittelwerte gleich den Mittelwerten
der virtuellen Werte pro
Stratum sind.
niedrig
Im niedrig-Stratum wurden 2
UEen in die v-Gruppe und 3 in
die b-Gruppe, im hoch-Stratum
wurden 3 in die v-Gruppe und 2
in die b-Gruppe gewählt.
Die bedingten Gruppen-Mittelwerte sind:
E(Yv | X=v, Z=n)=25 bzw.
E(Yb | X=b, Z=n)=55 und
E(Yv | X=v, Z=h)=50 bzw.
E(Yb | X=b, Z=h)=75.
hoch
Motivation
20
Die Differenzen zwischen den
Mittelwerten der behandelten
und vergleichsbehandelten
Gruppe
Der PF-Kausaleffekt pro Stratum:
D(Z=zi ) =
E(Yb | X=b, Z=zi) - E(Yv| X=v, Z=zi).
Auch hier wird deutlich, dass die
bedingten Gruppen-Mittelwerte
von den obigen bedingten
virtuellen Mittelwerten abweichen
können.
Für die beiden Strata sind die PF-Kausaleffekte in der obigen Graphik dargestellt:
D(Motivation=n) = 55-25 =30
D(Motivation=h) = 75-50 =25
PF-Kausaleffekt-Mittel =
D(Z=z1)p(Z= z1)+...
...+ D(Z=zi)p(Z= zi); wobei p(Z=zi)
der Anteil der UE im i. Stratums ist
Das PF-Kausaleffekt-Mittel über die PFKausaleffekte beider Strata beträgt:
30 * 0.50 + 25 * 0.50 = 27.5
(in jedem Stratum sind jeweils 5 UEen von
10; daher ist der Anteil jeweils 0.50).
v
b
X: Gruppe
Verteilung der möglichen
Ergebnisse bei Motivationsstratifizierter Randomisierung
0.2
Anteil
E(Yb| X=b, Z=zi) bzw.
E(Yv| X=v, Z=zi)
Mittelwerts-Differenzen ,
(= PF-Kausaleffekte)
in den Motivationsgruppen
Für das ‚niedrig’- bzw. ‚hoch’Stratum wird jeweils per Zufall
für jede Person entschieden, ob
sie ein Skript bekommt.
0.15
0.1
0.05
0
-10 0
Skriptbeispiel(Fortsetzung): Bei jeweils 5
UEen in jedem Stratum können pro Stratum
nun jeweils 10 verschiedene Aufteilungen in
eine 2er bzw. 3er-Gruppen erzeugt werden.
Damit alle Möglichkeiten berücksichtigt
werden, müssen insgesamt 100 (=10*10, bei
zwei Strata) Ergebnisse berechnet werden.
Für alle 100 möglichen Experimente wurden
die Kausaleffekte über die Strata gemittelt.
Die Graphik(links) zeigt die Verteilung all
PF-Kausaleffekt-Mittel
dieser Ergebnisse.
Im schlimmsten Fall ist der PF-Kausaleffekt 2 bzw. 48, allerdings kommt das selten vor. Die
Chance, einen Wert in der Nähe des wahren Kausaleffekts zu erhalten (=25) erhöht sich auch
gegenüber der einfachen Randomisierung beträchtlich.
10 20 30 40 50 60
Die Gruppenmittelwerte sollen nur
dann für die Berechnung des kausalen
Effekts verwendet werden, wenn folgende bedingten Unabhängigkeitsforderungen (hier für die Mittelwerte
formuliert) gelten:
E(Yb| Z=zi) = E(Yb| X=b , Z=zi ),
E(Yv| Z=zi) = E(Yv| X=v , Z=zi)
D.h. die Mittelwerte über die virtuellen
Werte sollen pro Stratum gleich groß
sein wie die Gruppenmittelwerte
Für das Skriptbeispiel formuliert bedeutet die
bedingte Unabhängigkeitsforderung für beide
Strata die Forderungen
(28=) E(Yv | Z=n) = E(Yv | X=v, Z=n) (=25)
bzw.
(53=) E(Yb | Z=n) = E(Yb | X=b, Z=n) (=55)
Die Forderung ist hier nicht erfüllt.
(50=) E(Yv | Z=h) = E(Yv | X=v, Z=h) (=50)
bzw.
(75=) E(Yb | Z=h) = E(Yb | X=b, Z=h) (=75)
Die Forderung ist hier erfüllt.
Bei der Stratifizierung können auch mehrere Merkmale simultan berücksichtigt werden.
Auch bei der stratifizierten Randomisierung sollte zusätzlich nach Durchführung des Experiments die Strategie
der Konstanthaltung als Vorsichtsmaßnahme angewandt werden, da ja eventuell über die Stratifizierungsmerkmale hinaus weitere Merkmale den kausalen Effekt stören könnten.
4.9.2.2.2.2 Nichtexperimentelle Untersuchungen: Konstanthaltung
Nagl, Einführung in die Statistik
Seite 177
Nach der WOLDschen Empfehlung wird in einem ‚Gedankenexperiment’ geklärt, welche Variable die
Treatment- bzw. welche die Responsevariable ist. Insgesamt sollten sich die Überlegungen für die Feststellung
der Kausalität an die Prinzipien von Experimenten anlehnen; oft wird auch von quasi-experimentellen
Untersuchungen gesprochen.
Grundsätzlich entfallen hier die Randomisierungsmöglichkeiten, umso wichtiger sind nun die Konstanthaltungstechniken. Das Experimentalparadigma zeigt auf, daß sich diese Techniken aber auf Variablen beschränken sollen, die zeitlich vor der Treatmentvariable anzusetzen sind (Pre-Treatmentvariablen).
Ein zentrales Problem ist hier die große Anzahl möglicherweiser relevanter Pre-Treatmentvariablen, die konstantgehalten werden sollten; das erfordert i.a. große Stichproben. Aber trotz großer Stichproben sind zumindest
partielle Konfundierungen nicht vermeidbar. Zusätzliche Annahmen über die Art des prädiktiven Zusammenhangs (z. B. Linearität) der Variablen sind erforderlich, wenn sehr viele Variablen simultan konstantgehalten
werden sollen. Ebenso wichtig sind fundierte theoretische Überlegungen, die bei der Auswahl der konstantzuhaltenden relevanten Pre-Treatmentvariablen behilflich sind.
Übungsaufgaben (4.5)
1.
Berechnen Sie für folgende x,y-Paare (Angst,IQ): (80,100) (75,140) (68,130) (77,120)
1.1. Die Kreuztabelle der ordinalen Paarvergleiche
1.2. Die ordinalen Korrelationskoeffizienten: KENDALLS a, KENDALLS b, STUARTS c , GOODMANKRUSKALS  , KIMs d x y , SOMERs d x y , KIMs d x y , SOMERs d x y .
2.
Gegeben sei die Häufigkeitstabelle für zwei dichotome Merkmale (a, b, c, d sind die Häufigkeiten):
y=0
y=1
x=0
a
b
x=1
c
d
2.3. Berechnen Sie die beiden Koeffizienten für a=3, b=3, c=0,d=4 (siehe auch Skript Kap. 4.5.1)
2.1. Berechnen Sie GOODMAN-KRUSKALS 
2.2. Berechnen Sie KIMs d x y .
3.
Für verschiedene Berufe wurde ermittelt, wer seine Aufgabe mit wenig bzw. mehr überzeugter
Pflichterfüllung durchführt. Dabei sei folgende Kreuztabelle erzielt worden (Kreuztabelle mit Häufigkeiten):
Pflichterfüllung
3.1.
3.2.
3.3.
3.4.
3.5.
Beruf
0: klein
1: mittel
2:hoch
Mesner
1
1
3
Mechaniker
2
1
0
Professor
0
1
4
Bilden Sie alle ordinalen Paarvergleiche (y: Defektprozentsatz)
Erzeugen Sie die Gruppenpaarvergleichshäufigkeitstabelle
Erzeugen Sie die Modalprädiktionsregeln
Berechnen Sie ein lambda für diese Modalprädiktionsregeln
Stellen Sie die Modalprädiktionsregeln übersichtlich dar in Form einer Vergleichsmatrix der Länder
und als HASSE-Diagramm