Prof. Dr. J. Pannek Dynamics in Logistics Vorkurs Mathematik

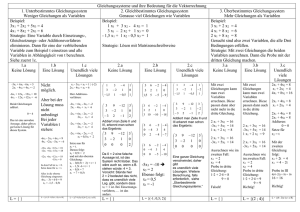
Prof. Dr. J. Pannek
Dynamics in Logistics
Vorkurs Mathematik für Ingenieure
WS 2015/2016 — Übung 5
Aufgabe 1 : Lineare Gleichungssysteme
(a) Bestimmen Sie die Lösungen folgender Gleichungssysteme:
0,9x−0,7y+7,3 = 0, 2 8x + 3y = 36 13x−15y+17
(i) (v) 1,2x−0,2y+8,9
5x + y = 12 6,5x−7,5y+8,5 = 0, 6 3, 2x − 1, 7y
=
46
(x + 1)(y + 8)
=
(y + 5)(x + 3)
(ii) (vi)
−2, 7x + 0, 7y = −30
(2x − 3)(5y + 7) = 2(y + 1)(5x − 6)
(x − 4)(y + 7) = (x − 3)(y + 4) 4
+
y
=
x
(vii) (iii) 2
3
(x + 5)(y − 2) = (x + 2)(y − 1)
= 7−2y 5−3x
14x − 15y = 24a 12x − 5y = 22 (viii) (iv) 10x − 21y = 24b 12x + 3y = 6 (b) Bestimmen Sie die Lösungen folgender Gleichungssysteme:
x1 + 2x2 + x3 = 1 x1 + 2x2 + 3x3 = 10 (v) 2x1 + 3x2 + x3 = 1 (i) 2x1 + 3x2 + x3 = 13 x1 + 3x2 + 2x3 = 2 3x1 + x2 + 2x3 = 13 x1 + 2x2 + x3
2x1 + x3
=
1
=
5
2
= 5 (vi) 2x1 + 4x2 + 2x3 =
(ii) 3x1 + x2
−x1 − 2x2 − x3 = −1
x1 + x2 − x3 = 0 ax1 + bx2 − cx3
x1 + 2x2
= c
= 4 = b
= 10 (vii) ax1 − bx2 + cx3
(iii) x2 + 3x3
−ax1 + bx2 + cx3 = a
x1 + 3x2 + 3x3 = 15 x1 + x2 = 2c x1 + 3x2 + 2x3 = 24 (viii) x1 + x3 = 2b (iv) 2x1 + x2 + 5x3 = 31 x2 + x3 = 2a 3x1 + 4x2 + 2x3 = 40 (c) Bestimmen Sie die Lösungen folgender Gleichungssysteme:
(i) Welche zwei Zahlen haben folgende Eigenschaften? Vergrößert man jede um 5, so
wird die Differenz ihrer Quadrate um 100 größer, während ihr Produkt um 325
zunimmt.
(ii) Vergrößert man jede von zwei Zahlen um 2, so verhalten sich die Zahlen wie 3:4.
Subtrahiert man dagegen von jeder der beiden Zahlen 3, haben die so erhaltenen
Zahlen das Verhältnis 2:3. Wie heißen die beiden Zahlen?
Vorkurs Mathematik für Ingenieure
WS 2015/2016
(iii) Die Summe zweier Zahlen beträgt 1000. Multipliziert man die erste Zahl mit 2, die
zweite mit 3, so ist die Summe der Produkte 2222. Wie groß ist jede der beiden
Zahlen?
(iv) Die beiden Vororte X und Y einer Großstadt bilden mit deren Zentrum Z ein Dreieck.
Von X über Z nach Y beträgt die Entfernung 12km, Y liegt 2km weiter vom Zentrum
entfernt als X. Wie weit sind die beiden Vororte X und Y vom Stadtzentrum Z
entfernt?
Lösung:
(a) Zwei lineare Gleichungen mit zwei Variablen
(i)
8x + 3y = 36 ⇔ 23y
= 276
x = 0 ⇔ y = 12
8x + 3y = 36
5
5x + y = 12 | · 8 ←
−+
(ii)
3, 2x − 1, 7y = 46 2,7
−2, 7x + 0, 7y = −30 | · 3, 2 ←
+
−
3, 2x − 1, 7y = 46 ⇔ −2, 35y
= 28, 2
x = 8 ⇔ y = −12
(iii)
(x − 4)(y + 7) = (x − 3)(y + 4)
(x + 5)(y − 2) = (x + 2)(y − 1)
3x − y = 16
⇔ −+
−x + 3y = 8 | · 3 ←
3x − y = 16
⇔ 8y
= 40
y = 5
⇔ x = 7
(iv)
12x − 5y = 22
12x + 3y = 6 | · −1 ←
−+
12x − 5y = 22
⇔ −8y
= 16
x = 1 ⇔ y = −2
(v)
0,9x−0,7y+7,3 = 0, 2
13x−15y+17
1,2x−0,2y+8,9
6,5x−7,5y+8,5 = 0, 6
⇔
⇔
⇔
⇔
0, 9x − 0, 7y + 7, 3
1, 2x − 0, 2y + 8, 9
−1, 7x + 2, 3y =
−2, 7x + 4, 3y =
−1, 7x + 2, 3y =
−1, 1y
=
x = 7, 3
y = 3, 7
= 0, 2(13x − 15y + 17) = 0, 6(6, 5x − 7, 5y + 8, 5)
2,7
−3, 9
−3, 8 | · (−1, 7) ←
−+
−3, 9 −4, 07
Vorkurs Mathematik für Ingenieure
WS 2015/2016
(vi)
(x + 1)(y + 8) = (y + 5)(x + 3) (2x − 3)(5y + 7) = 2(y + 1)(5x − 6)
⇔
⇔
⇔
⇔
xy + 8x + y + 8
=
xy
+
5x
+
3y
+
15
10xy + 14x − 15y − 21 = 10xy + 10x − 12y − 12
3x − 2y = 7
4
4x − 3y = 9 | · (−3) ←
−+
3x − 2y = 7
y
= 1
x = 3 y = 1
(vii)
4 + y =
2
5−3x =
x 3 7−2y
⇔
⇔
⇔
⇔
−x + y =
−4 2(7 − 2y) = 3(5 − 3x)
−x + y = −4
9
9x − 4y = 1 ←
−+
−x + y = −4 5y
= −35
x = −3
y = −7
(viii)
14x − 15y = 24a
10
10x − 21y = 24b | · (−14) ←
−+
14x − 15y =
24a
⇔ 144y
= 240a − 336b
x = 7 − 5 2a
2b ⇔ y= 5 − 7
3a
3b
(b) Drei lineare Gleichungen mit drei Variablen
(i)
x1 + 2x2 + 3x3 = 10
2
3
2x1 + 3x2 + x3 = 13 | · (−1) ←
−+
3x1 + x2 + 2x3 = 13 | · (−1) ←−−− +
x1 + 2x2 + 3x3
⇔ x2 + 5x3
5x2 + 7x3
x1 + 2x2 + 3x3
⇔ x2 + 5x3
18x3
x1 = 3 ⇔ x2 = 2
x3 = 1 = 10
5
= 7 = 17 | · (−1) ←
−+
= 10
= 7 = 18
Vorkurs Mathematik für Ingenieure
WS 2015/2016
(ii)
2x1 + x3
3
=
5
3x1 + x2
= 5 | · (−2) ←
−+
x1 + x2 − x3 = 0 | · (−2) ←−−− +
2x1 + x3
⇔ −2x2 + 3x3
−2x2 + 3x3
2x1 + x3
⇔ −2x2 + 3x3
0
x1
⇔ x2
x3 beliebig
= 5
= 5
= 5 | · (−1) ←
−+
= 5
= 5
= 0
= − 21 x3 + 52 = 32 x3 − 52 (iii)
x1 + 2x2
(−1)
=
4
x2 + 3x3
= 10
x1 + 3x2 + 3x3 = 15 ←
−+
x1 + 2x2
⇔ x2 + 3x3
−x2 − x3
x1 + 2x2
⇔ x2 + 3x3
0
= 4 = 10 = −11 ←
−+
= 4 = 10 = −1
Das System hat keine Lösung.
(iv)
x1 + 3x2 + 2x3 = 24
(2) (3)
2x1 + x2 + 5x3 = 31 | · (−1) ←
−+
3x1 + 4x2 + 2x3 = 40 | · (−1) ←−−−− +
x1 + 3x2 + 2x3
⇔ 5x2 − x3
5x2 + 4x3
x1 + 3x2 + 2x3
⇔ 5x2 − x3
5x3
x1 = 6 ⇔ x2 = 4
x3 = 3 = 24
(−1)
= 17
−+
= 32 ←
= 24
= 17
= 15
(v)
x1 + 2x2 + x3 = 1
2
2x1 + 3x2 + x3 = 1 | · (−1) ←
−+
x1 + 3x2 + 2x3 = 2 | · (−1) ←−−− +
x1 + 2x2 + x3
⇔ x2 + x3
−x2 − x3
x1 + 2x2 + x3
⇔ x2 + x3
0
x1
=
⇔ x2
=
x3 beliebig
= 1 = 1 = −1 ←
−+
= 1
= 1
= 0
x3 − 1 −x3 + 1
Vorkurs Mathematik für Ingenieure
WS 2015/2016
(vi)
x1 + 2x2 + x3 = 1 2
2x1 + 4x2 + 2x3 = 2 | · (−1) ←
−+
−x1 − 2x2 − x3 = −1 ←−−−−−−−−−− +
x1 + 2x2 + x3
⇔ 0
0
x1
=
⇔ x2 beliebig
x3 beliebig
= 1
= 0
= 0 ←
−+
−2x2 − x3 + 1
(vii)
ax1 + bx2 − cx3 = c ax1 − bx2 + cx3 = b | · (−1) ←
−+
−ax1 + bx2 + cx3 = a ←−−−−−−−−−− +
ax1 + bx2 − cx3
⇔ 2bx2 − 2cx3
2bx2
ax1 + bx2 − cx3
⇔ 2bx2 − 2cx3
2cx3
x1 = b+c 2a ⇔ x2 = a+c
2b x3 = a+b 2c
=
c (−1)
= −b + c
−+
= a+c ←
=
c = −b + c
= a+b (viii)
x1 + x2 = 2c x1 + x3 = 2b | · (−1) ←
−+
x2 + x3 = 2a
x1 + x 2 =
2c
(−1)
⇔ x2 − x3 = −2b + 2c
x2 + x3 =
←
−+
2a
x1 + x2 =
2c
⇔ x2 − x3 =
−2b + 2c 2x3
= 2a + 2b − 2c
x1 = −a + b + c
⇔ x2 = a − b + c x3 = a + b − c (c) Sachaufgaben
(i) Die beiden Zahlen seien x und y.
(x + 5)2 − (y + 5)2 = x2 − y 2 + 100
(x + 5)(y + 5)
=
xy + 325 ⇔
⇔
⇔
⇔
x2 + 10x + 25 − y 2 − 10y − 25 = x2 − y 2 + 100
xy + 5x + 5y + 25
=
xy + 325 10x − 10y = 100
−1
5x + 5y = 300 | · 2 ←
−+
10x − 10y = 100
20y
= 500
x = 35
y = 25
Vorkurs Mathematik für Ingenieure
WS 2015/2016
(ii) Die beiden Zahlen seien x und y.
x+2 = 3 y+2
4
x−3
⇔
y−3 = 32 4(x + 2) =
3(x − 3) =
4x − 3y =
⇔ 3x − 2y =
4x − 3y =
⇔ −y
=
x = 13
⇔ y = 18
(iii) Die beiden Zahlen seien x und y.
x + y = 1000
(−2)
2x + 3y = 2222 ←
−+
3(y + 2)
2(y − 3)
3
−2
3 | · (−4) ←
−+
−2 −18
x + y
⇔ y
x =
⇔ y =
= 1000
= 222 778
222
(iv) Die Entfernung von X zu Z sei x, die Entfernung von Y zu Z sei y.
x + y = 12 x + y = 12 ⇔ y
x − y = −2 | · (−1) ←
= x + 2
−+
x + y = 12
⇔ 2y
= 14
x = 5 ⇔ y = 7