Näherung für π durch das Werfen von Münzen

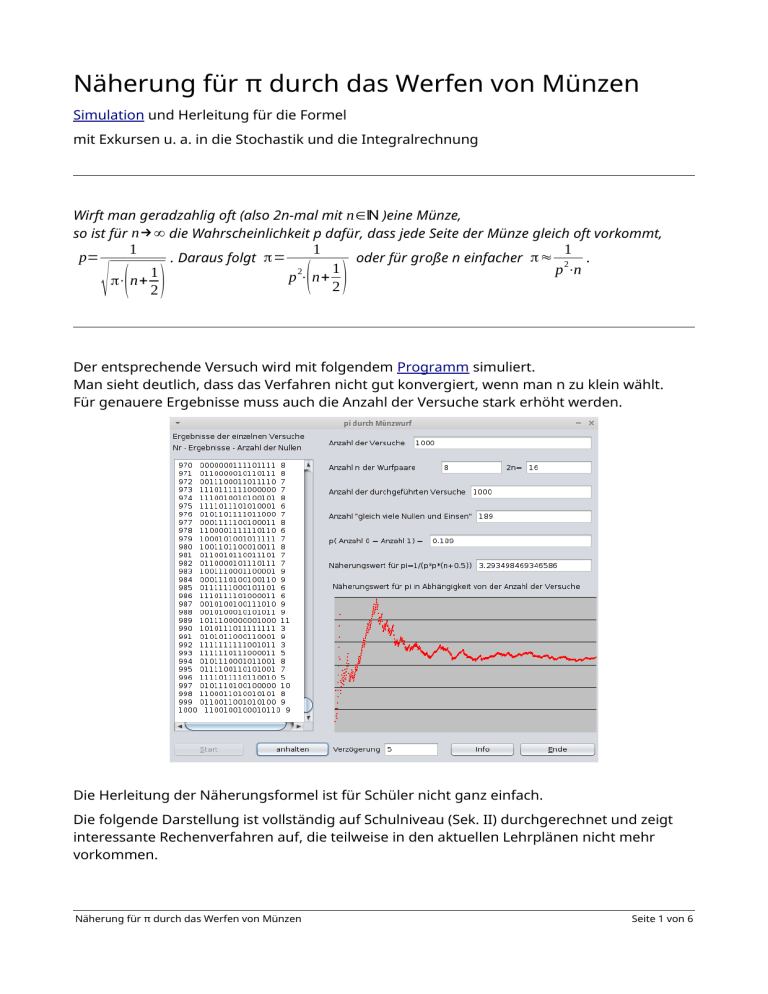
Näherung für π durch das Werfen von Münzen
Simulation und Herleitung für die Formel
mit Exkursen u. a. in die Stochastik und die Integralrechnung
Wirft man geradzahlig oft (also 2n-mal mit n∈ℕ )eine Münze,
so ist für n→∞ die Wahrscheinlichkeit p dafür, dass jede Seite der Münze gleich oft vorkommt,
p=
√
1
( )
π⋅ n+
1
2
1
. Daraus folgt π=
( 12 )
oder für große n einfacher π≈
p 2⋅ n+
1
.
2
p ⋅n
Der entsprechende Versuch wird mit folgendem Programm simuliert.
Man sieht deutlich, dass das Verfahren nicht gut konvergiert, wenn man n zu klein wählt.
Für genauere Ergebnisse muss auch die Anzahl der Versuche stark erhöht werden.
Die Herleitung der Näherungsformel ist für Schüler nicht ganz einfach.
Die folgende Darstellung ist vollständig auf Schulniveau (Sek. II) durchgerechnet und zeigt
interessante Rechenverfahren auf, die teilweise in den aktuellen Lehrplänen nicht mehr
vorkommen.
Näherung für π durch das Werfen von Münzen
Seite 1 von 6
1.
Berechnung der Wahrscheinlichkeit dafür, dass bei 2n Würfen beide
Seiten einer Münze gleich häufig auftreten
Bei jedem Wurf einer Münze ergeben sich die 2 Ereignisse Kopf (0) oder Zahl (1).
Bei zwei Würfen gibt es 4 Ereignisse: 00, 01, 10, 11
Mit jeder geworfenen Münze verdoppelt sich die Anzahl der möglichen Ereignisse.
2n
Bei 2n Würfen sind es also 2 Ereignisse.
Die Wahrscheinlichkeit für ein Ereignis beim 2n-fachen Wurf beträgt dann also
1
.
2n
2
Bei wie vielen dieser Ergebnisse kommen denn aber n-mal 0 und n-mal 1 vor?
Es liegt hier ein Ziehen ohne Zurücklegen vor, bei dem die Reihenfolge keine Rolle spielt.
Wenn man n Nullen aus 2n Nullen zieht, so hat man für die erste Null 2n Möglichkeiten, für
die zweite Null noch 2n-1 Möglichkeiten usw. bis zu 2n-(n-1) Möglichkeiten für die n-te Null.
Die Anzahl aller Möglichkeiten ergibt sich durch Multiplikation dieser Werte:
2 n⋅(2n−1)⋅(2 n−2)⋅...⋅(2 n−(n−1))
Mit der Fakultätsschreibweise n !=1⋅2⋅3⋅...⋅(n−1)⋅n schreibt man einfacher
(2 n−n)⋅(2 n−(n+1))⋅...⋅2⋅1
(2 n)!
(2 n)!
2 n⋅( 2n−1)⋅(2 n−2)⋅...⋅(2 n−(n−1))⋅
=
=
.
(2 n−n)⋅(2 n−(n+1))⋅...⋅2⋅1 (2 n−n)!
n!
Da es auf die Reihenfolge nicht ankommt, muss man das Ergebnis noch durch die Anzahl
dividieren, die die Anordnungsmöglichkeiten der n Nullen angibt:
Für die erste Null hat man n Möglichkeiten, für die zweite Null sind es (n-1) Möglichkeiten
usw. bis zu 1 Möglichkeit für die n-te Null. Wieder ergibt die Multiplikation der Werte die
Anzahl aller Anordnungsmöglichkeiten: n⋅(n−1)⋅(n−2)⋅...⋅3⋅2⋅1=n!
( 2n)!
(2 n) !
n!
Die gesuchte Zahl der Möglichkeiten (n-mal Null, n-mal Eins) ist also
=
.
n!
n!⋅n !
Zieht man allgemein aus n Kugeln k Kugeln ohne Zurücklegen und ohne Berücksichtigung
der Reihenfolge, so ist die Zahl der Möglichkeiten
()
abkürzende Schreibweise.
Also kann man hier auch schreiben
()
n!
= n mit dem Binom n als
k !⋅(n−k)! k
k
(2 n)!
(2 n)!
=
= 2n
n!⋅n ! n !⋅(2 n−n)!
n
( )
Die Wahrscheinlichkeit für n-mal Null und n-mal Eins beim 2n-fachen Münzwurf ergibt sich
2n
(
n)
dann zu p=
.
2
2n
Näherung für π durch das Werfen von Münzen
Seite 2 von 6
2.
Andere Schreibweise für p
Beweis durch vollständige Induktion
2n
(
n ) 1⋅3⋅5⋅...⋅(2 n−3)⋅(2 n−1)
Es gilt p=
=
2
2n
2⋅4⋅6⋅...⋅(2 n−2)⋅ 2 n
Beim Beweisverfahren der vollständigen Induktion zeigt man zunächst, dass für irgendein n
die Formel gilt. Am besten nimmt man dazu das kleinstmögliche n, hier also n=1.
Dann zeigt man, dass bei Gültigkeit der Formel für n=k die Formel auch für n=k+1 gilt.
Dann gilt (Dominoeffekt), dass die Formel nicht nur für n=1, sondern auch für n=2 und dann
auch für n=3 usw. gilt, also für alle n∈ℕ .
Beweis:
n=1:
2!
2
2!
1⋅2
(
)
1
1 !⋅(2−1)! 1!⋅1! 1⋅1 2 1
links steht dann
=
=
=
= =
2
rechts steht nur
2⋅1
4
4
4
4
2
(2 n−1) (2−1) 1
1
, da für n=1 gilt
=
=
2
2n
2
2
nicht notwendig, aber zur Anschaulichkeit auch noch folgender Fall:
n=2:
4!
4
4!
1⋅2⋅3⋅4 24
(
)
2
4 !⋅(4−2) ! 2!⋅2 ! 1⋅2⋅1⋅2
4
6 3 1⋅3
links steht
=
=
=
= = = =
22⋅2
rechts steht
24
16
16
16
16
8
2⋅4
1⋅...⋅(2 n−1) 1⋅...⋅(2⋅2−1) 1⋅...⋅3 1⋅3
=
=
=
2⋅...⋅ 2 n
2⋅...⋅ 2⋅2
2⋅...⋅4 2⋅4
2k
(
k ) 1⋅3⋅5⋅...⋅(2 k−3)⋅(2 k−1)
Nun soll für n=k gelten
=
2⋅4⋅6⋅...⋅(2 k −2)⋅ 2 k
22 k
Es muss nun gezeigt werden, dass dann die Formel auch für n=k+1 gilt, dass also
+ 1)
(2(k( k +1)
) = 1⋅3⋅5⋅...⋅(2(k +1)−3)⋅(2(k +1)−1) = 1⋅3⋅5⋅...⋅(2 k−1)⋅( 2 k+ 1)
2⋅4⋅6⋅...⋅(2( k +1)−2)⋅ 2(k + 1)
22(k+1)
linke Seite:
2⋅4⋅6⋅...⋅(2 k )⋅( 2k + 2)
+ 1)
+2)!
(2 k + 2)!
(2(k(k +1)
) = (2kk+1+2) = ( k +1) !⋅(2(2kk+2−(k
+1))! (k +1)!⋅(k +1)!
=
=
22(k+1)
22 k +2
22 k⋅22
22 k⋅22
( )
( )
(2k ) !⋅(2 k +1)⋅(2 k +2) (2 k )! (2 k +1)⋅(2 k +2) 2 k (2 k +1)⋅2⋅(k +1) 2 k (2 k +1)⋅2
k
k
k !⋅k !⋅( k +1)⋅( k+ 1)
(k + 1)⋅(k +1)
k !⋅k ! (k +1)⋅(k+ 1)
k +1
= 2k ⋅
= 2k ⋅
= 2k ⋅
2k
4
4
4
2 ⋅4
2
2
2
(2kk )⋅ 2kk+1+1 = (2kk )⋅2k + 1
2
2k
2
2
2k
2k + 2
einsetzen
=
1⋅3⋅5⋅...⋅(2 k −3)⋅(2 k −1) 2 k +1
gleich rechte Seite.
⋅
2⋅4⋅6⋅...⋅(2 k−2)⋅ 2 k
2 k +2
Näherung für π durch das Werfen von Münzen
Seite 3 von 6
3.
Der Zusammenhang zwischen dem Wallisschen Produkt und der
gefundenen Wahrscheinlichkeit
2
2
2
2
2
2 ⋅4 ⋅6 ⋅...⋅(2 n−2) ⋅(2 n)
Das Wallissche Produkt ist gegeben durch π =lim 2 2 2
.
2 n→∞ 1 ⋅3 ⋅5 ⋅...⋅(2 n−1)2⋅(2n+ 1)
1⋅3⋅5⋅...⋅(2 n−3)⋅(2 n−1)
12⋅32⋅52⋅...⋅(2n−3)2⋅(2 n−1)2
2
Mit p=
folgt p = 2 2 2
und weiter
2⋅4⋅6⋅...⋅(2 n−2)⋅ 2 n
2 ⋅4 ⋅6 ⋅...⋅(2 n−2)2⋅ (2n)2
2 2 2
2
2
22⋅4 2⋅62⋅...⋅(2 n−2)2⋅ (2 n)2 2n+ 1
1 2 ⋅4 ⋅6 ⋅...⋅(2 n−2) ⋅ (2 n)
=
=
⋅
p2 12⋅32⋅52⋅...⋅(2 n−3)2⋅(2n−1)2 12⋅32⋅52⋅...⋅(2 n−3)2⋅( 2n−1)2 2n+ 1
Für großes n ergibt sich näherungsweise
2 2 2
2
2
1 2 ⋅4 ⋅6 ⋅...⋅(2 n−2) ⋅ (2 n) 2n+ 1
=
⋅
p2 12⋅32⋅52⋅...⋅(2 n−3)2⋅(2n−1)2 2n+ 1
Durch Umstellen folgt
≈
π⋅(2 n+1)
2
1 π
1
1
1
≈ ⋅(2 n+1)=π⋅(n+ ) → π≈
≈ 2 für großes n.
2
2
1
2
p 2
p ⋅(n+ ) p ⋅n
2
Mit Hilfe der Formel π=
1
( )
1
p ⋅ n+
2
2
4.
Wallissches Produkt
wurde die Simulation (Java-Programm) programmiert.
Herleitung des Wallisschen Produktes mit Hilfe partieller Integration
Aus der Produktregel
( u(x )⋅v ( x ) ) ' =u ' (x )⋅v( x)+u(x )⋅v ' ( x ) oder kurz (u⋅v) '=u '⋅v+ u⋅v '
ergibt sich durch Integration
x1
x1
x1
x0
x0
x0
∫ (u⋅v)' dx=∫ u '⋅v dx+∫ u⋅v ' dx .
Da sich Differentiation und anschließende Integration gegenseitig aufheben, steht auf der
x1
linken Seite
∫ (u⋅v)' dx=[ u⋅v ] x
x1
0
.
x0
Durch Umformen ergeben sich die beiden folgenden Formeln:
x1
x1
x0
x0
[ u⋅v ] x =∫ u '⋅v dx+∫ u⋅v ' dx →
x1
0
x1
x1
x1
x0
x0
x1
∫ u'⋅v dx =[ u⋅v ] x −∫ u⋅v ' dx ; ∫ u⋅v ' dx= [ u⋅v ] x −∫ u'⋅v dx
x1
0
x0
x1
0
x0
π
2
Mit Hilfe der rechten Formel soll nun das Integral
∫ sin n x dx
berechnet werden.
0
Man setzt u(x )=sin
n−1
x ; v ' ( x)=sin x .
Dann folgt (Potenzregel und Kettenregel) u ' (x )=(n−1)⋅sin
Näherung für π durch das Werfen von Münzen
n−2
x⋅cos x und v ( x )=−cos x .
Seite 4 von 6
Also gilt
π
2
π
2
0
0
π
2
π
x⋅sin x dx= sinn −1 x⋅(−cos x) 2 −∫ ((n−1)⋅sin n−2 x⋅cos x )⋅(−cos x) dx
∫ sin n x dx=∫ sinn−1
[ u
]0
u
v'
v
v
u'
0
Nebenrechnungen:
integralfreier Summand:
[
π
] (
sinn−1 x⋅(−cos x ) 2 = sin n−1 π⋅ −cos π −( sinn−1 0⋅(−cos 0) ) =(1⋅0)−0⋅(−1)=0
2
2
u
v
0
))
(
rechtes Integral:
π
2
π
2
x ) dx=(n−1)⋅∫ sinn−2 x⋅(−cos 2 x )dx
∫ ( (n−1)⋅sin n−2 x⋅cos x )⋅(−cos
v
u'
0
=
2
0
π
2
(n−1)⋅∫ sin
2
sin x+ cos x=1
π
2
n−2
0
x⋅( sin x−1)dx=( n−1)⋅∫ ( sin x−sin
2
n
π
2
n−2
0
Damit folgt
π
2
π
2
π
2
0
0
0
x ) dx=( n−1)⋅∫ sin x dx−(n−1)⋅∫ sin
n
0
π
2
0
0
n⋅∫ sin n x dx=( n−1)⋅∫ sinn−2 x dx →
n−2
x dx
0
Addition des linken Summanden auf der rechten Seite
∫ sin n x dx=−(n−1)⋅∫ sinn x dx +(n−1)⋅∫ sin n−2 x dx
π
2
π
2
→
π
2
π
2
0
0
⋅∫ sinn−2 x dx
∫ sinn x dx= n−1
n
Das Ergebnis ist eine Rekursionsformel: das linke Integral wird vereinfacht, indem der
Exponent im rechten Integral um 2 verringert wird. Durch wiederholtes Anwenden der
Formel kann so das linke Integral gelöst werden.
Beispiel für n=6:
π
2
π
2
π
2
π
2
0
0
0
0
π
5
⋅π
∫ sin6 x dx= 56⋅∫ sin4 x dx= 56⋅ 34 ∫ sin 2 x dx= 56⋅34⋅12⋅∫ 1 dx= 56⋅34⋅12⋅[ x ]02 = 56⋅34⋅12⋅π2 = 32
Beispiel für n=5:
π
2
π
2
π
2
π
8
∫ sin5 x dx= 45⋅∫ sin3 x dx= 45⋅23 ∫ sin x dx= 45⋅23⋅[ −cos x ] 02 = 45⋅23⋅(0+1)= 15
0
0
0
Man kann schon an diesen Beispielen sehen, dass bei einem geraden Exponenten von sin x
bei den Brüchen die ungeraden Zahlen im Zähler und die geraden Zahlen im Nenner stehen.
Außerdem wird der Faktor π angehängt.
Für ungeraden Exponenten sind dagegen die geraden Zahlen im Zähler und die ungeraden
Zahlen im Nenner. Ein Faktor π fehlt hier.
π
2
Im Folgenden werden die Integrale
∫ sin2 n +1 x dx , ∫ sin2 n x dx
0
Da für 0≤x< π die sin-Werte kleiner als 1 sind, gilt
2
Näherung für π durch das Werfen von Münzen
π
2
0
π
2
und
∫ sin2 n−1 x dx
verglichen.
0
π
2
π
2
π
2
0
0
0
∫ sin2 n +1 x dx≤∫ sin2 n x dx≤∫ sin 2 n−1 x dx .
Seite 5 von 6
π
2
Allgemein gilt
∫ sin2 n x dx =
0
π
2
(2 n−1)⋅(2 n−3)⋅...⋅3⋅1 π
⋅
(2 n)⋅(2 n−2)⋅...⋅4⋅2 2
(2 n)⋅(2 n−2)⋅...⋅4⋅2
∫ sin2 n +1 x dx= (2 n+1)⋅(2 n−1)⋅...⋅3⋅1
π
2
( 2n−2)⋅(2 n−4)⋅...⋅4⋅2
∫ sin2 n−1 x dx= (2 n−1)⋅(2 n−3)⋅...⋅3⋅1
und
0
0
Aus der oben genannten Ungleichungskette folgt (Division durch den linken Term)
(2 n)⋅(2 n−2)⋅...⋅4⋅2
( 2n−1)⋅(2 n−3)⋅...⋅3⋅1 π
(2 n−2)⋅(2n−4 )⋅...⋅4⋅2
≤
⋅ ≤
(2 n+1)⋅(2 n−1)⋅...⋅3⋅1
(2 n)⋅(2 n−2)⋅...⋅4⋅2 2
(2 n−1)⋅(2 n−3)⋅...⋅3⋅1
1 ≤
(2 n+1)⋅(2 n−1)2⋅(2 n−3)2⋅...⋅32⋅12 π
2n+1
1
⋅ ≤
= 1+
2
2
2 2
2
2
n
2
n
(2 n) ⋅(2 n−2) ⋅...⋅4 ⋅2
1 = lim (1 ) ≤ lim
n→∞
n→∞
Daraus folgt lim
n→∞
(
(
)
→
Grenzwert fürn →∞
→
(2 n+1)⋅(2 n−1)2⋅( 2n−3)2⋅...⋅32⋅12 π
1
⋅ ≤ lim 1+
= 1
2
2
2 2
2
2n
n →∞
(2 n) ⋅(2 n−2) ⋅...⋅4 ⋅2
2
2
2
2
(
)
)
(2 n+1)⋅(2 n−1) ⋅(2 n−3) ⋅...⋅3 ⋅1 π
⋅ =1
2
(2 n)2⋅(2 n−2)2⋅...⋅42⋅22
(
)
(2 n)2⋅(2 n−2)2⋅...⋅42⋅22
π
oder =lim
(Wallissches Produkt).
2 n→∞ (2 n+1)⋅(2n−1)2⋅(2 n−3)2⋅...⋅32⋅12
Man beachte, dass der Faktor (2 n+1) nicht quadriert wird!
5.
Schlussbemerkung
Das Gleichheitszeichen im Wallisschen Produkt gilt nur, wenn der Grenzwert des Bruchs
bestimmt wird.
Beim oben beschriebenen Zufallsversuch ist man natürlich gezwungen, den Wert für n relativ
klein zu halten. Das Gesetz der großen Zahl ist hier deshalb nicht anwendbar, d. h. auch eine
sehr große Anzahl an durchgeführten Würfelergebnissen wird nicht eine beliebig genau
Annäherung an den richtigen π-Wert ergeben.
Die Simulation erlaubt viele Versuche bei großem n durchzuführen. Aber auch dabei wird aus
dem Graphen deutlich, dass dieses Verfahren zur Bestimmung der Nachkommastellen von π
nicht sinnvoll ist.
1
Bestimmt man mit Hilfe einer Tabellenkalkulation auf Grund der Formel π=
2
( 12 )
p ⋅ n+
die π-Werte für wachsendes n (beim Bruch wird bis zum n-ten Faktor im Zähler und Nenner
multipliziert), so sieht man leicht, dass die Werte sich von unten an π annähern.
Erst für n≈500 ergeben sich die ersten 2 Nachkommastellen richtig (3,14).
Näherung für π durch das Werfen von Münzen
Seite 6 von 6