Mathematische Hilfsmittel

1
Mathematische Hilfsmittel
2
Lateinische Schrift
a b c d e f g h i j k l m n o p q r s t u v w
x y z ß ä ö ü
A B C D E F G H I J K L M N O P Q R S T
U V W X Y Z Ä Ö Ü
Griechische Schrift
α
β
Alpha
Beta
ν
ξ
Ny
Α
Ksi
Β
Alpha
Ny
ο
Omikron
Γ
Beta
Ν
γ
Gamma
Gamma
Ξ
Ksi
Ο
Omikron
δ
Delta
π
Pi
∆
Delta
ε
Epsilon
ρ
Sigma
Ε
Zeta
Rho
Epsilon
Π
Pi
ς
Zeta
Ρ
Rho
σ
Ζ
Σ
Sigma
Eta
η
Theta
ϑ
Jota
τ
Ypsilon
υ
ϕ
Tau
Η
Eta
Τ
Tau
Θ
Theta
Υ
Ypsilon
ι
Phi
Ι
Jota
Φ
Phi
κ
Kappa
χ
Chi
Κ
Kappa
Χ
Chi
λ
µ
Lambda
ψ
Psi
My
ω
Omega
Λ
Μ
Ψ
Omega
Lambda
Psi
My
Ω
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
3
1 Lineare Algebra
1.1 Mengen
Definition 1-1
Eine Menge ist eine Zusammenfassung wohlunterschiedener Objekte unserer Anschauung
oder unseres Denkens zu einem Ganzen. Die Objekte werden Elemente der Menge genannt.
Definition 1-2
Die leere Menge Æ ist eine Menge, die kein Element enthält.
Definition 1-3
Die Mengen A und B heißen gleich, wenn jedes Element von A auch Element von B ist und
umgekehrt.
Definition 1-4
B ist eine Teilmenge von A, wenn jedes Element von B auch Element von A ist: B ⊆ A.
Definition 1-5
Die Vereinigungsmenge von A und B (A ∪ B) ist die Menge, die aus allen Elementen besteht,
die zu A oder B, oder beiden gehören.
Zahlenmengen
Menge der natürlichen Zahlen
ÍN = {1,2,3...}
Menge der ganzen Zahlen
ÙZ = {...-2,-1,0,1,2..}
Menge der rationalen Zahlen
ÐQ = {
p
|p ∈ Z und q∈ Z}
q
Die Menge der reellen Zahlen R besteht aus den rationalen Zahlen und den irrationalen Zahlen.
4
1.2 Koordinaten
Definition 1-6
Koordinaten1 dienen dazu, Punkte in der Ebene oder im Raum festzulegen. Dazu ist ein Koordinatensystem erforderlich. Das am häufigsten verwendete ist das kartesische2 (rechtwinklige) Koordinatensystem. Im einfachsten Fall, der Ebene, besteht es aus zwei zueinander senkrechten Zahlengeraden, den Koordinatenachsen, die sich im Nullpunkt schneiden. Sie bilden
das Achsenkreuz. Der gemeinsame Ursprung wird Nullpunkt oder Koordinatenanfangspunkt
genannt (Abb. 1-1).
Abb. 1-1 Kartesische Koordinaten eines Punktes P
Definition 1-7
Im Fall räumlich kartesischer Koordinaten
ist die Orientierung der Achsen ist wie folgt
festgelegt: Schauen wir gegen die z-Richtung
(also von oben), so geht die positive x-Achse
durch eine Linksdrehung um 90° in die positive y-Achse über. Die drei Achsen bilden ein
Rechtssystem. Je zwei Achsen spannen eine
Ebene im Raum auf, diese bilden ein ebenes
kartesisches Koordinatensystem. Es gibt die
x-y-Ebene, die x-z-Ebene und die y-z-Ebene
Abb. 1-2: Räumliche kartesische Koordinaten
1
(Abb. 1-2)
zu kon ... und lat. ordinare = ordnen, also etwa ›einander Zugeordnete‹
René Descartes, latinisiert Renatus Cartesius, frz. Philosoph, Mathematiker und Naturwissenschaftler, 15961650
2
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
5
Definition 1-8
Das ebene Polarkoordinatensystem besteht
aus einem Punkt 0 (dem Pol) der Ebene und
einem von 0 ausgehenden Fahrstrahl, der Polarachse. Die Darstellung eines Punktes P
erfolgt durch das ebene Polarkoordinatenpaar
(r, ϕ), wobei r der Abstand von P zum 0Punkt und ϕ der Winkel ist, den die x-Achse
mit dem Fahrstrahl 0-P einschließt (Abb. 1-3).
Abb. 1-3: Ebene Zylinderkoordinaten
Definition 1-9
Im räumlichen Zylinderkoordinatensystem
(Abb. 1-4) sind die Koordinatenflächen einmal
die zur z-Achse senkrechten Ebenen
(z = konst.), die von der z-Achse ausgehenden Halbebenen (ϕ = konst.) und die Zylinderflächen, deren Achse die z-Achse ist
(r = konst.).
Abb. 1-4: Räumliche Zylinderkoordinaten
Definition 1-10
Im räumlichen Polarkoordinatensystem ist neben einem Punkt 0 als Pol und einer von 0
ausgehenden Polarachse eine Ebene (Polarebene) angegeben, die die Polarachse enthält.
Abb. 1-5: Räumliche Polarkoordinaten (Kugelkoordinaten)
6
Ein Punkt im Raum wird durch das Tripel (r, ϕ, ϑ) eindeutig bestimmt. Dabei ist r der Abstand des Punktes P vom Punkt 0, ϕ der Winkel zwischen der Polarachse und der Projektion
der Strecke 0P in die x-y- Ebene und ϑ der Winkel zwischen 0P und dem von 0 ausgehen-
den, auf der x-y-Ebene senkrecht stehenden Strahl, der zusammen mit der Polarachse ein
Rechtssystem bildet.
Definition 1-11
Unter einer Koordinatentransformation1 wird der Übergang von einem Koordinatensystem
mit den Koordinaten zu einem anderen Koordinatensystem mittels Transformationsgleichungen verstanden.
Definition 1-12
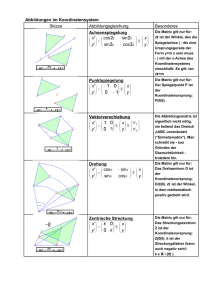
Transformation ebener kartesischer Koordinaten bei einer Parallelverschiebung des Koordinatensystems (Abb. 1-6).
x = u−b
y = v−a
⇔
u =x+b
v= y+a
Abb. 1-6: Parallelverschiebung kartesischer Koordinaten
Definition 1-13
Transformation ebener kartesischer Koordinaten bei einer Drehung des Koordinatensystems
(Abb. 1-7).
x = u cos ϕ − v sin ϕ
y = u sin ϕ + v cos ϕ
1
lat. transferre = hinübertragen, hinüberbringen
⇔
u = x cos ϕ + y sin ϕ
v = − x sin ϕ + y cos ϕ
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
7
Abb. 1-7: Drehung eines kartesischen Koordinatensystems
Definition 1-14
Transformation kartesischer Koordinaten in räumliche Zylinderkoordinaten
x = r cos ϕ
y = r sin ϕ
z=z
r = x 2 + y2
ϕ = arctan
y
x
z=z
Abb. 1-8: Räumliche Zylinderkoordinaten, ebene Polarkoordinaten und z-Richtung
Definition 1-15
Transformation kartesischer Koordinaten in räumliche Polarkoordinaten (Kugelkoordinaten)
x = rcos ϕsin ϑ
y = rsin ϕsin ϑ
z = rcos ϑ
r = x 2 + y2 + z2
y
ϕ = arctan
x
x 2 + y2
ϑ = arctan
z
Definitionsbereiche:
0≤r≤∞
−π<ϕ≤π
0≤ϑ≤π
8
Abb. 1-9 Räumliche Polarkoordinaten, Kugelkoordinaten
2 Definitionen und Rechenregeln für Vektoren
Definition 2-1
Ein Skalar1 ist eine reelle Zahl.
Definition 2-2
Ein Vektor2 entspricht einer physikalischen Größe, die einen Betrag und eine Richtung hat3.
Eine Vektorgröße kann zur geometrischen Interpretation durch einen Pfeil dargestellt werden,
dessen Länge den Betrag und dessen Spitze die Richtung und die Orientierung angibt. Beispiele für vektorielle physikalische Größen sind Kraft, Geschwindigkeit, Beschleunigung. Die
Definition zeigt, dass für die Angabe einer vektoriellen Größe mehr als eine Zahl erforderlich
ist und dass sich eine vektorielle Größe beim Übergang in ein anderes Koordinatensystem in
bestimmter Weise transformiert.
Definition 2-3
Abb. 2-1 Freie Vektoren
1
Abb. 2-2 Linienflüchtige Vektoren
zu lat. scalaris = zur Leiter, Treppe gehörig
lat. vector = Träger, Fahrer, zu lat. vehere = fahren
3
William Rowan Hamilton, irischer Mathematiker und Physiker, 1805-1865
2
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
9
Aus der Definition geht hervor, dass sich ein Vektor bei der Parallelverschiebung nicht ändert
(Abb. 2-1). Diese Vektoren werden als freie Vektoren bezeichnet. Ein linienflüchtiger Vektor
(Abb. 2-2) darf nur längs seiner Wirkungslinie verschoben werden (eingeschränkte Parallelverschiebung).
Definition 2-4
Ein gebundener Vektor hat einen festen
Anfangspunkt P, er darf überhaupt nicht verschoben werden (Abb. 2-3).
Abb. 2-3 Gebundener Vektor
Beispiel 2-1
Freier Vektor:
An einem starren Körper angreifendes Drehmoment.
Linienflüchtiger Vektor:
An einem starren Körper angreifende Kraft.
Gebundener Vektor:
Ortsvektor, an einem deformierbaren Körper angreifende
Kräfte und Momente.
Definition 2-5
Die Länge eines Vektors ist sein Betrag, und wir schreiben:
a =a≥0
Definition 2-6
Abb. 2-4 Multiplikation eines Vektors mit einem Skalar
Ist a ein Vektor und λ eine reelle Zahl, so bezeichnet das Symbol λa einen Vektor mit folgenden Eigenschaften (Abb. 2-4):
1. Der Vektor λa ist parallel zu a
2. λ > 0 ⇒ a und λa sind gleichgerichtet
3. λ < 0 ⇒ a und λa sind entgegengesetzt gerichtet
4. Der Betrag von λa ist:
λa = λ a
10
Es bedeuten weiterhin:
λ = 1:
Der Vektor a bleibt unverändert.
λ = 0:
Es entsteht ein Vektor vom Betrag 0, der Null-Vektor, der keine bestimmte
Richtung hat.
λ = -1:
Der Richtungssinn von a wird umgekehrt.
Zwei parallele Vektoren können sich damit nur um einen skalaren Faktor unterscheiden.
Definition 2-7
Ein Einheitsvektor e ist durch e = 1 definiert. Zu jedem Vektor a kann damit ein gleichgerichteter Einheitsvektor gefunden werden (Abb. 2-5)
Abb. 2-5 Der Einheitsvektor
Da
1
1
a
a den Betrag a = = 1 hat, gilt:
a
a
a
0
a =
a
a
Jeder Vektor lässt sich somit in der Form Betrag mal zugehöriger Einheitsvektor darstellen:
a =aa
0
Definition 2-8
Zwei Vektoren a und b wird durch den Operator „+“ ein neuer Vektor zugeordnet, den
man die Vektorsumme von a und b nennt.
Zur Bildung von a und b wird b durch Parallelverschiebung im Endpunkt von a angetragen. Der Vektor a + b weist vom AnfangsAbb. 2-6 Vektoraddition, Parallelogrammgesetz
punkt von a zum Endpunkt von b.
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
11
Entsprechend Abb. 2-6 lässt sich die Vektorsumme auch derart bilden, dass der Vektor a durch
Parallelverschiebung im Endpunkt von b angetragen wird. Der Vektor a + b weist vom Anfangspunkt von b zum Endpunkt von a.
Auf diese Weise entsteht ein Parallelogramm
mit den orientierten Seiten a und b und der
orientierten Diagonalen a + b, das in der Mechanik die Anwendung beim Kräfteparallelogramm findet. In entsprechender Weise
Abb. 2-7 Subtraktion von Vektoren
lässt sich die Differenz a − b = a + ( − b ) bilden.
Definition 2-9
Es gilt:
a) a − a = 0
b) a + b = b + a
c) (a + b) + c = a + (b + c) = a + b + c Assoziativ-Gesetz (Abb. 2-8)
Abb. 2-8 Assoziativgesetz der Addition
Definition 2-10
Mit n Vektoren a 1 ,a 2 ,a 3 ,...a n , und mit den Koeffizienten λ1 ,λ 2 ,λ 3 ,...., λ n , welche als reelle
Zahlen variabel sind, können wir eine lineare Schar von Vektoren bilden:
λ1 a 1 + λ 2 a 2 + λ 3 a 3 + ...... + λ n a n
Wir nennen n Vektoren linear unabhängig, wenn sich aus ihnen durch Linearkombination
der Nullvektor
λ1 a 1 + λ 2 a 2 + λ 3 a 3 + ...... + λ n a n = 0
nur durch
λ1 = λ 2 = λ 3 = ..... = λ n = 0
12
bilden lässt. Andernfalls sind die Vektoren linear abhängig. Lineare Abhängigkeit bedeutet
also, dass die obige Gleichung für wenigstens einen nicht verschwindenden Skalar λi erfüllt
ist und damit nach einem Vektor aufgelöst werden kann. Unterstellen wir λ 1 ≠ 0 , erhalten wir
a1 als Linearkombination, Überlagerung oder Superposition:
a1 = −
λ
λ2
λ
a 2 − 3 a 3 − .... − n a n
λ1
λ1
λ1
Die geometrische Bedeutung der linearen Abhängigkeit erkennen wir aus den folgenden Beispielen.
Beispiel 2-2
n = 2 λ1 , λ 2 ≠ 0
Aus λ1 a1 + λ 2 a 2 = 0 folgt, dass a1 und a2 ein
und derselben Geraden parallel sind. Die Vektoren a1 und a2 heißen dann kollinear. Alle Vektoren, die zu einer Geraden (der Wirkungslinie
von a1 ) parallel sind, lassen sich in der Form
Abb. 2-9 Kollineare Vektoren
a g = λ a1 darstellen (Abb. 2-9).
Beispiel 2-3
n = 3, λ 1 , λ 2 , λ 3 ≠ 0;
a 1 , a 2 linearunabhängig . Aus λ 1 a 1 + λ 2 a 2 + λ 3 a 3 = 0 folgt,
dass a1, a2, a3 in einer Ebene liegen. Wir sagen: a1, a2, a3 sind komplanar1.
Definition 2-11
Jeder Vektor, der zu derjenigen Ebene parallel ist, die durch die beiden linear unabhängigen
Vektoren a1 und a2 aufgespannt wird, lässt sich in der Form a e = 1 a 1 + 2 a 2
darstellen (Abb. 2-10)
Abb. 2-10 Komplanare Vektoren
1
zu lat. complanare = einebnen
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
13
Beispiel 2-4
n = 4, λ 1,λ 2 ,λ 3,λ 4 ≠ 0;
a 1,a 2 ,a 3 linear unabhängig
Im dreidimensionalen Raum gilt der
Satz 2-1
Mehr als 3 Vektoren sind stets linear abhängig. Zwischen 4 beliebigen Vektoren besteht also
immer eine Beziehung
λ1 a 1 + λ 2 a 2 + λ 3 a 3 + λ 4 a 4 = 0
Beispiel 2-5
Sind a 1 , a 2 , a 3 drei linear unabhängige Vektoren, so lässt sich jeder beliebige Vektor des
dreidimensionalen Raumes durch Linearkombination in a 1 , a 2 , a 3 darstellen, also:
a r = 1 a1 + 2 a 2 + 3 a 3
Abb. 2-11 Basissystem im räumlichen Fall
Satz 2-2
Drei linear unabhängige Vektoren bilden im Raum ein Basissystem
Hinweis: Die zahlenmäßige Darstellung vektorieller Größen muss so erfolgen, dass wir ver-
schiedene Vektoren auch ohne geometrische Anschauung miteinander vergleichen können.
Dazu müssen wir im Raum ein Basissystem vorgeben. Da je drei beliebige, linear unabhängige Vektoren eine Basis bilden, gibt es für die Darstellung ein und derselben vektoriellen Größe unendlich viele verschiedene Möglichkeiten. Im Unterschied dazu ist die zahlenmäßige
Angabe einer skalaren Größe von der Wahl des Bezugssystems unabhängig.
Definition 2-12
Ist die Basis durch die Vektoren g1 ,g 2 ,g 3 gegeben, so heißt die Gleichung
a = a 1 g1 + a 2 g 2 + a 3 g 3
14
die Komponentendarstellung1 des Vektors a zur Basis g i (i = 1,2,3) .
a 1 , a 2 , a 3 = KoordinatendesVektors a
a 1 g 1 , a 2 g 2 , a 3 g 3 = KomponentendesVektors a
Je nach Anordnung der Basisvektoren g i unterscheiden wir (Abb. 2-12) zwischen einem
Rechts- oder Linkssystem.
Abb. 2-12 Rechts- bzw. Linkssystem
Definition 2-13
Die Drehung von g 1 auf dem kürzesten Wege in g 2 und die Richtung von g 3 bilden ein
Rechtssystem.
Definition 2-14
Es seien e x ,e y ,e z drei Einheitsvektoren, die zueinander orthogonal sind (orthonormierte Ba-
sis). und in dieser Reihenfolge ein Rechtssystem bilden. Ein Vektor a kann dann als Summe
der 3 Vektoren a x e x ,a y e y ,a z e z dargestellt werden (Abb. 2-13).
Wir schreiben:
a = a x ex + a y ey + a z ez
= {a x , a y , a z } < e x , e y , e z >
Hinweis: Die in Spitzklammern hinzugefügte
Basis kann entfallen, wenn Verwechslungen
ausgeschlossen sind. Für die Basisvektoren
Abb. 2-13 Kartesische Koordinaten
1
zu lat. componere = zusammenstellen
folgt dann die Komponentendarstellung
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
15
e x = {1,0,0}; e y = {0,1,0}; e z = {0,0,1}
Den Betrag des Vektors a entnehmen wir der Abb. 2-13
a = a = a 2x + a 2y + a 2z
Der Ortsvektor
r = x ex + y ey + z ez = {x, y, z}
ist ein gebundener Vektor. Er dient dazu, die Lage
eines Punktes P im Raum anzugeben.
Abb. 2-14 Der Ortsvektor
Definition 2-15
Den Zylinderkoordinaten r, ϕ, z werden die Basisvektoren er, eϕ, ez zugeordnet, die wie ex, ey,
ez eine Orthonormalbasis bilden (Abb. 2-15). Dabei gelten die folgenden Beziehungen:
e r = cos ϕe x + sin ϕe y = {cos ϕ,sin ϕ,0}
eϕ = − sin ϕe x + cos ϕe y
ez = ez
= {− sin ϕ, cos ϕ,0}
= {0,0,1}
und umgekehrt:
e x = cos ϕe r − sin ϕeϕ ={cos ϕ,− sin ϕ,0}
e y = sin ϕe r + cos ϕeϕ ={sin ϕ, cos ϕ,0}
ez = ez
={0,0,1}
Abb. 2-15 Zylinderkoordinaten
16
Ein beliebiger Vektor a kann dann sowohl auf die Basis ex, ey, ez als auch auf die Basis er, eϕ,
ez bezogen werden. Statt
a = ax ex + ay ey + az ez = {ax, ay, az}
ist dann
a = a r e r + a ϕ eϕ + a z e z = {a r , a ϕ , a z }
zu schreiben, und für den Betrag des Vektors a erhalten wir:
a = a = a 2r + a ϕ2 + a 2z
Mit den obigen Gleichungen folgt dann
ar =
a x cos ϕ + a y sin ϕ
a ϕ = −a x sin ϕ + a y cos ϕ
az = az
und umgekehrt:
a x = a r cos ϕ − a ϕ sin ϕ
a y = a r sin ϕ + a ϕ cos ϕ
az = az
Dabei ist zu beachten, dass ein Vektor a, je nachdem welchem Punkt im Raum wir ihn zuordnen, zwar stets die gleichen Koordinaten ax, ay, az , jedoch jeweils andere Koordinaten ar, aϕ
besitzt, da die Einheitsvektoren er und eϕ von ϕ abhängen (Abb. 2-16).
Abb. 2-16 Abhängigkeit des Vektors a von den Einheitsvektoren
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
17
Der Ortsvektor r hat in Zylinderkoordinaten, d.h. bei Bezugnahme auf die Orthonormalbasis er, eϕ, ez die Form:
r = r e r + ze z
bzw. : r = {r,0,z}
Achtung: Die Polarkoordinate r ist nicht
mit dem Betrag des Ortsvektors zu verAbb. 2-17 Ortsvektor in Zylinderkoordinaten
wechseln (Abb. 2-17).
Definition 2-16
Zwei Vektoren sind gleich, wenn sie komponentenweise gleich sind
a = b⇔
a x = bx , a y = by , a z = bz
Einer Vektorgleichung im Raum entsprechen somit drei skalare Gleichungen.
Definition 2-17
Ein Vektor wird mit einem Skalar multipliziert, indem alle seine Komponenten mit dem Skalar multipliziert werden.
λa = λ{a x ,a y ,a z } = {λa x , λa y ,λa z }
Definition 2-18
Für die Summe bzw. Differenz zweier Vektoren gilt:
a ± b = {a x ± b x ,a y ± b y ,a z ± b z }
Definition 2-19
0 = {0,0,0}
Der Nullvektor hat in jedem Bezugssystem die Koordinaten 0.
18
Definition 2-20
Das skalare Produkt (oder auch innere
Produkt) a ⋅ b der beiden Vektoren a und
b liefert einen Skalar, der wie folgt definiert ist:
a ⋅ b = a b cos ϕ
Abb. 2-18 Skalarprodukt zweier Vektoren a und b
Definition 2-21
Für die Basisvektoren folgt:
⋅
ex
ey
ez
ex
1
0
0
ey
0
1
0
ez
0
0
1
oder kurz
e j ⋅ e k = δ jk
j, k = x , y, z
δ jk = 1
für j = k
δ jk = 0 sonst
Definition 2-22
Mit der Definition sind:
a) a ⋅ b = b ⋅ a
b)
c)
(λa ) ⋅ b = a ⋅ (λ b) = λa ⋅ b
(a + b ) ⋅ c = a ⋅ c + b ⋅ c
denn es gilt (Abb. 2-19):
a + b cos γ = a cos α + b cos β und damit
(a + b ) ⋅ c = a + b ⋅ c cos γ
= a c cos α + b c cos β = a ⋅ c + b ⋅ c
womit das Skalarprodukt auf die Koordinaten
Abb. 2-19 Distributivgesetz
zurückgeführt werden kann:
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
19
a ⋅ b = (a x e x + a y e y + a z e z ) ⋅ (b x e x + b y e y + b z e z ) =
a x bx ex ⋅ ex
a ybx ey ⋅ ex
a z b x ez ⋅ ex
+ a x b y ex ⋅ ey
+ a yby ey ⋅ ey
+ a z b y ez ⋅ e y
+ a x bz ex ⋅ ez +
+ a y bz e y ⋅ ez +
+ a z bz ez ⋅ ez
und damit
a ⋅ b = a x bx + a yby + a zbz
a x bx + a yby + a zbz
cos ϕ =
Insbesondere gilt:
2
x
a + a 2y + a 2z b 2x + b 2y + b 2z
2
2
a ⋅ a = a = a 2x + a 2y + a 2z = a = a 2
Definition 2-23
Die Orthogonalitätsbedingung für zwei Vektoren (a ,b ≠ 0) :
a x bx + a yb y + a zbz = 0
Definition 2-24
Projektion eines Vektors auf eine vorgegebene Richtung
Wir entnehmen der Abb. 2-20:
0
a b = a b b = a cos ϕ
b b ab cos ϕ
=
b
bb
b2
bzw.
ab =
und damit der Betrag des Vektors a b
Abb. 2-20 Projektion von a auf die Richtung von b
a b = a b = a cos ϕ
a⋅b
b
2
b
b ab cos ϕ a ⋅ b
=
=
2
2
b
b
b
Liegt statt b ein Einheitsvektor e vor, so ist wegen e = 1
a e = (a ⋅ e )e
20
und
ae = a ⋅ e
Insbesondere gilt
a x = a ⋅ ex
a y = a ⋅ ey
a z = a ⋅ ez
Für die Winkel zwischen einem Vektor a und den Basisvektoren gilt dann:
Abb. 2-21 Winkel zwischen a und dem Basisvektor ex
cos α x =
a
ax
a
cos α y = y ;cos α z = z
a
a
a
Richtungskosinusse
cos 2 α x + cos 2 α y + cos 2 α z = 1
Die Komponenten eines Einheitsvektors im orthonormierten Basissystem sind die Kosinusse der Winkel zwischen dem Einheitsvektor
und den Koordinatenachsen:
e = {cos α x , cos α y ,cos α z }
Abb. 2-22 Richtungskosinusse des Einheitsvektors
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
21
Definition 2-25
Das vektorielle Produkt (oder äußere Produkt) zweier Vektoren a und b wird a × b geschrieben und wie folgt definiert (Abb. 2-23)
1. a × b ist ein Vektor.
2. a × b steht senkrecht auf a und senkrecht auf b.
3. a, b und a × b bilden in dieser Reihenfolge ein Rechtssystem.
4. Es ist a × b = a b sinϕ , also gleich dem Flächeninhalt A des von a und b gebildeten Parallelogramms.
Abb. 2-23 Das Vektorprodukt zweier Vektoren
Nach Definition 3 gilt für das Vektorprodukt das kommutative Gesetz nicht, vielmehr ist
a × b = −b × a
Sind die beiden Vektoren a und b parallel, so ist ϕ = 0 oder ϕ = π, dann ist a × b = 0 .
Es ist also a × b = 0 für:
a=0
und
b≠0
a≠0
und
b=0
a=0
und
b=0
a||b
(ϕ = 0 oder π)
Insbesondere ist also:
a×a = 0
Für die Einheitsvektoren gilt:
22
×
ex
ey
ez
ex
0
− ez
ey
ey
ez
0
− ex
ez
− ey
ex
0
Definition 2-26
Es gilt
a) λ(a × b ) = (λ a ) × b = a × (λ b ) = λ a × b
b)
(a + b ) × c = a × c + b × c
Definition 2-27
Zurückführung des Vektorproduktes auf die Koordinaten:
a × b = (a x e x + a y e y + a z e z )× (b x e x + b y e y + b z e z ) =
a x b x ex × ex
+ a x b y ex × ey
+ a x bz ex × ez
a ybx ey × ex
+ a yb y ey × ey
+ a y bz ey × ez
a z b x ez × e x
+
+
a z b y ez × e y
a z bz ez × ez
und
a × b = {a y b z − a z b y , a z b x − a x b z ,a x b y − a y b x }
dafür kann auch folgende Merkregel verwandt werden
ex
ey
ez
a × b = ax
ay
az
bx
by
bz
Achtung: Merkregel gilt so nur bei Bezugnahme auf eine orthogonale normierte Vektorbasis.
Definition 2-28
Das Spatprodukt [a , b, c] ist definiert als das Volumen V des von den Vektoren a, b und c
gebildeten Parallelepipeds (Abb. 2-24)
V = Ah = a × b c cos ϕ = (a × b ) ⋅ c
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
23
Abb. 2-24 Das Spatprodukt
Wir hätten auch
V = (b × c ) ⋅ a
V = (c × a ) ⋅ b
erhalten können. Insgesamt ist dann
[a,b,c] = (a × b ) ⋅ c = (b × c ) ⋅ a = (c × a ) ⋅ b
und es gilt die Regel von der zyklischen Vertauschbarkeit
[a ,b,c] = [b,c,a ] = [c,a ,b]
und wegen (b × c ) ⋅ a = a ⋅ (b × c ) ≡ (a × b ) ⋅ c die (sinnvolle) Vertauschbarkeit von ⋅ und ×
(a × b ) ⋅ c = a ⋅ (b × c )
Durch Ausrechnen von ( a × b) ⋅ c erhalten wir
[a,b,c] = (a y b z − a z b y )c x + (a z b x − a x bz )c y + (a x b y − a y b x )cz
wofür wir auch
[a,b,c] =
ax
ay
az
bx
by
bz
cx
cy
cz
hätten schreiben können. Für das Spatprodukt weisen wir noch die Beziehung
24
a1 ⋅ b1
[a1 ,a 2 ,a 3 ] [b1 ,b 2 ,b3 ] = a 2 ⋅ b1
a 3 ⋅ b1
a1 ⋅ b 2
a 2 ⋅ b2
a 3 ⋅ b2
a1 ⋅ b 3
a 2 ⋅ b3
a 3 ⋅ b3
nach, die für b1 = a1 ,b 2 = a 2 ,b3 = a 3 , in die Form
[a1,a 2 ,a 3 ]
2
a 1 ⋅ a1
= a 2 ⋅ a1
a 3 ⋅ a1
a1 ⋅ a 2
a2 ⋅ a2
a3 ⋅ a 2
a1 ⋅ a 3
a 2 ⋅ a3
a3 ⋅ a3
übergeht. Der Beweis erfolgt durch Ausrechnen mit a1 = {a1x ,a1y ,a1z } usw.
Definition 2-29
Zerlegung eines Vektors in der Ebene nach zwei Richtungen. Der Vektor a in Abb. 2-25 soll in
die vorgegebenen Richtungen a1 und a2 zerlegt werden, also a = λ1 a1 + λ 2 a 2 mit noch unbekannten λ 1 und λ 2 .
a = λ1 a1 + λ 2 a 2
a × a 2 = λ1 a1 × a 2
(a × a 2 ) ⋅ (a1 × a 2 ) = λ1 (a1 × a 2 )
|× a 2
|⋅ (a1 × a 2 )
2
und damit
λ1 =
Abb. 2-25 Zerlegung eines Vektors in der Ebene
λ1 =
(a × a 2 ) ⋅ (a1 × a 2 ) ;
(a1 × a 2 )2
(a × a 2 ) ⋅ (a1 × a 2 )
(a1 × a 2 )2
entsprechend erhalten wir λ 2 und damit insgesamt
λ2 =
(a1 × a ) ⋅ (a1 × a 2 )
(a1 × a 2 )2
Wenn a1 und a2 parallel sind, so ist a1 × a 2 = 0 , in diesem Falle ist keine Zerlegung möglich.
Sind in der Ebene mehr als zwei Richtungen vorgegeben, so ist die Zerlegung nicht eindeutig.
Definition 2-30
Zerlegung eines Vektors im Raum nach drei vorgegebenen Richtungen.
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
25
Für a gilt nach Abb. 2-26
a = λ1 a1 + λ 2 a 2 + λ 3 a 3
mit noch unbekannten λ1,λ2 und λ3.
a = λ1 a 1 + λ 2 a 2 + λ 3 a 3
|(a 2 × a 3 ) ⋅
(a 2 × a 3 ) ⋅ a = λ1 (a 2 × a 3 ) ⋅ a1
λ1 =
Abb. 2-26 Zerlegung eines Vektors im Raum
[a 2 , a 3 , a ] = [a , a 2 , a 3 ]
[a 2 , a 3 , a1 ] [a1 , a 2 , a 3 ]
Entsprechend folgen λ2 und λ3 und somit insgesamt
λ1 =
[a , a 2 , a 3 ] ;
[a1, a 2 , a 3 ]
λ2 =
[a1, a, a 3 ] ;
[a1, a 2 , a 3 ]
λ3 =
[a1 , a 2 , a ]
[a1, a 2 , a 3 ]
Wenn die Vektoren a1, a2 und a3 komplanar sind, so gilt [a1, a2, a3] = 0, und eine Zerlegung ist
in diesem Falle nicht möglich. Sind mehr als drei Richtungen vorgegeben, so ist die Zerlegung
nicht eindeutig.
Definition 2-31 (Mehrfache Produkte)
Für vektorielle Produkte aus drei Vektoren gilt die
Beziehung
a × (b × c) = (a ⋅ c)b − (a ⋅ b)c
wofür wir auch unter Berücksichtigung von
a × ( b × c) =
=
Abb. 2-27 Das zweifache Vektorprodukt
und damit
[
e [a ( b c
e [a ( b c
ex
ey
ez
ax
b ycz − bzc y
ay
bzcx − b x cz
az
b xc y − b ycx
[
e [a (b c
e [a (b c
]
− b c )] +
− b c )]
e x a y (b x c y − b y c x ) − a z (b z c x − b x cz ) +
y
z
y z
− b z c y ) − a x (b x c y
z
x
z x
− b x c z ) − a y (b y c z
]
− b c )]+
− b c )]
a × (b × c) =e x a y ( b x c y − b y c x ) − a z ( b z c x − b x c z ) +
y
z
y z
− b zc y ) − a x (b x c y
z
x
z x
− b x c z ) − a y (b yc z
y x
z y
y x
z y
26
schreiben können. Geometrisch ist sofort einleuchtend, dass der Vektor a × (b × c) in der
durch b und c aufgespannten Ebene liegt, da er zu b × c orthogonal ist. Für zweifache Vektorprodukte gilt das Assoziativgesetz nicht: a × (b × c) ≠ (a × b) × c
Definition 2-32
Es gilt:
a) (a × b) ⋅ (c × d ) = (a ⋅ c)(b ⋅ d) − (a ⋅ d)(b ⋅ c)
b) (a × b) × (c × d ) = [a , c, d ] b − [b, c, d ] a
= [a , b, d ]c − [a , b, c] d
c) a × (b × c) + b × (c × a ) + c × (a × b) = 0
2
2
d) (a × b) 2 = a b − (a ⋅ b) 2
Definition 2-33
Zerlegung eines Vektors a in zwei Komponenten, von denen eine parallel zu einem vorgegebenen Vektor e und die andere Komponente dazu senkrecht steht (Abb. 2-28), also
a = a || + a ⊥
Abb. 2-28 Vektorzerlegung parallel und senkrecht zu einer vorgegebenen Richtung
Mit a || = (a ⋅ e) e gilt: a ⊥ = a − a || = a − (a ⋅ e)e = (e ⋅ e)a − (a ⋅ e)e = e × (a × e)
und somit (Abb. 2-28)
a = (a ⋅ e)e + e × (a × e)
|| e
⊥e
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
27
3 Definitionen und Rechenregeln für Matrizen
Definition 3-1
Eine Matrix1 ist ein geordnetes Schema von Zahlen aik mit m Zeilen und n Spalten der Form
 a 11

a
A =  21
( m× n )

a
 m1
a 12
a 22
a m2
a 1n 

a 2n 


a mn 
Außer dem Zahlenwert eines Elementes aik ∈ R der Matrix A ist auch seine durch den Doppelindex i,k festgelegte Stellung im Schema, seine Zeilennummer i und seine Spaltennummer
k entscheidend. Eine Matrix mit m Zeilen und n Spalten ist eine Matrix vom Typ m × n (ge-
sprochen: m-Kreuz-n) oder kurz eine m × n -Matrix. Einzeilige Matrizen A( 1× n ) werden Zeilenvektoren und einspaltige Matrizen A( m × 1 ) werden Spaltenvektoren genannt und mit
T
kleinen Buchstaben bezeichnet. Es ist a i der i-te Zeilenvektor
a i = (a i1
T
a i 2 a in )
und ak der k-te Spaltenvektor
 a 1k 


 a 2k 
ak = 



a 
 mk 
Spezielle Matrizen
a) Nullmatrix
0
( m× n )
alle a ij = 0, i = 1, … , m,
b) Quadratische Matrix
m=n
c) Diagonalmatrix
m = n, a ij = 0 für i ≠ j
1
lat. Quelle, Ursache
j = 1, … , n
28



D =
( m× m ) 



d) Einheitsmatrix der Ordnung m
a 11
0
0
…
0
0
a 22
0





a mm 
0
0
0
I , a ij = 0, i ≠ j, a ii = 1
( m× m )
1 0 
0 1 I =
( m× m )

0 0 
0

0
0

1 
Definition 3-2
Zwei Matrizen sind gleich, wenn sie in allen Elementen übereinstimmen:
A = B
( m× n )
⇔ a ij = b ij für alle i,j
( m× n )
Definition 3-3
Zu jeder Matrix A wird eine transponierte1 Matrix AT nach folgender Vorschrift gebildet:
 a 11

a
A =  21
( m× n )

a
 m1
oder kurz
a 12
a 22
a m2
a 1n 

a 2n 


a mn 
A
( n×m )
A = (a ik )
A
( 2×3 )
Satz 3-1
1
a 21
a 22
a 2n
A T = (a ki )
 1 3


A =  5 2
(3×2 )
 4 6


Es gilt:
T
 a 11

a
=  12

a
 1n
(A )
T T
=A
lat. transponere = übersetzen, hinüberschaffen lassen
T
1 5 4

= 
3 2 6
a m1 

a m2 


a mn 
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
29
Definition 3-4
Es gilt die folgende Rechenregel:
(A + B) T = A T + B T
Definition 3-5
Eine quadratische Matrix, für die A = A T gilt, heißt symmetrisch.
4

A= 2

1
1

−3 −2

−2 7 
2
Definition 3-6
Eine quadratische Matrix A heißt antimetrisch (schiefsymmetrisch), wenn gilt:
A T = −A
Die Definition erfordert offensichtlich, dass die Hauptdiagonalelemente verschwinden.
 0 2

A =  −2 0

 1 −2
−1

2

0
Definition 3-7
Eine quadratische Matrix, in der alle Elemente unterhalb der Hauptdiagonalen Null sind heißt
obere Dreiecksmatrix (Rechtsdreiecksmatrix).
 a 11

 0
A =
(n×n )

 0

a 12
a 22
0
a 1n 

a 2n 


a nn 
Definition 3-8
Eine quadratische Matrix, in der alle Elemente oberhalb der Hauptdiagonalen Null sind heißt
untere Dreiecksmatrix (Linksdreiecksmatrix).
 a 11

a
A =  21
(n×n )

a
 n1
0
a 22
a n2
0 

0 


a nn 
30
Definition 3-9
Zwei Matrizen gleicher Dimension werden addiert (subtrahiert), indem ihre entsprechenden
Elemente addiert (subtrahiert) werden.
C = A ± B
( m× n )
⇔
( m×n ) (m×n )
c ij = a ij ± b ij ; i = 1, …, m, j = 1, …, n
Definition 3-10
Eine Matrix A wird mit einem Skalar λ multipliziert, indem jedes Element der Matrix mit λ
multipliziert wird:
B =λ A
( m× n )
( m×n )
⇔ b ij = λa ij ,
 λa 11

 λa
B = λA = A =  21

 λa
 m1
i = 1, …, m, j = 1, …, n
λa 12
λa 22
λa m 2
λa 1n 

λa 2 n 


λa mn 
Satz 3-2
Für Matrizen gleicher Dimension gilt:
a) A + 0 = 0 + A = A
b) A + (− A ) = 0
c) A + B = B + A
d) (A + B) + C = A + (B + C ) = A + B + C
e) λ(A + B) = λA + λB
f) (λ1 + λ 2 )A = λ1 A + λ 2 A
Definition 3-11
Es sei A eine m × n und B eine n × p Matrix, dann gilt für die Produktmatrix C = A ⋅ B ,
dass sie die Dimension m × p hat und dass sich ihre Elemente cij als Skalarprodukt aus dem
i-ten Zeilenvektor von A und dem j-ten Spaltenvektor von B ergeben:
 a 1T 
 T
a 
A = 2 
( m× n )
 
aT 
 m
n
c ij = a i b j = ∑ a ik b kj ,
T
k =1
B = (b1 , b 2 ,… , b p )
( n ×p )
i = 1,2, …, m ; j = 1,2, …, p
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
31
Beispiel 3-1
 3
 2 −4 6 

⋅ 4
 −3 6 −9 
 2
1 −3
3
6
5
  2 26 10 −14
2 0 = 

21
  −3 −39 −15
4 −4
oder auch
 1 2 0
 2 −4 6 

 ⋅ 3 −4 −4
 −3 6 −9 
1 −1
 2
0
  2 26 10 −14
5 = 

21
  −3 −39 −15
1
Für die Matrizenmultiplikation gilt nicht das Kommutativgesetz, d.h., i.a. ist:
A⋅B ≠ B⋅A
 1 2 3
 1 0 0
 4 2 7
 1 2 3








A =  2 1 3; B =  0 1 2 ; A ⋅ B =  5 1 5 ; B ⋅ A =  6 7 5 .
 2 3 1
1 0 1
 3 3 7
 3 5 4








Einheitsmatrizen reproduzieren beim Multiplizieren, sie spielen also die Rolle der 1 beim
Multiplizieren reeller Zahlen:
 1 0 0  1 2 3  1 2 3  1 2 3  1 0 0

 
 
 
 

 0 1 0 ⋅  2 1 3 =  2 1 3 =  2 1 3 ⋅  0 1 0

 
 
 
 

 0 0 1  2 3 1  2 3 1  2 3 1  0 0 1
 1 0 0  1 2  1 2  1 2

 
 
 
  1 0
 0 1 0 ⋅  2 1 =  2 1 =  2 1 ⋅  0 1

 
 
 

 0 0 1  2 3  2 3  2 3
Satz 3-3
Es gilt:
 A + B  ⋅ C = A ⋅ C+ B ⋅ C
 (m×n ) (m×n )  (n×p ) (m×p ) (m×p )
A ⋅  B + C  = A ⋅ B+ A ⋅ C
 (n×p ) (n×p )  (m×p ) (m×p )
( m× n )
Definition 3-12
Der Zeilenrang (Spaltenrang) einer Matrix ist die Anzahl der linear unabhängigen Zeilen
(Spalten) der Matrix.
32
Satz 3-4
Der Zeilenrang einer beliebigen Matrix ist immer gleich dem Spaltenrang. Es gilt, dass der
Rang von A nie größer ist als das Minimum aus Zeilenzahl und Spaltenzahl:
rg(A) ≤ min(m, n ) .
Andernfalls heißt A singulär.
Definition 3-13
Unter der Voraussetzung, dass die Produkte herstellbar sind, gilt für die Matrizenmultiplikation das Assoziativgesetz:
(A ⋅ B) ⋅ C = A ⋅ (B ⋅ C)
Definition 3-14
Eine Matrix A wird mit einem Faktor λ multipliziert, indem jedes Element der Matrix mit λ
multipliziert wird:
λA = λ(a ik ) = (λa ik )
bzw.:
 λa 11

 λa
λA = Aλ =  21

 λa
 m1
λa 12
λa 22
λa m 2
λa 1n 

λa 2 n 


λa mn 
Definition 3-15
Für das Transponieren von Matrizenprodukten gilt:
(λA) T = λA T , (A ⋅ B) T = B T ⋅ A T
Hinweis: Das Produkt zweier Matrizen kann die Nullmatrix sein, ohne dass einer der beiden
Faktoren die Nullmatrix ist.
 3
 2 −4 6 
⋅ 4

 −3 6 −9 
 2
1 −3
3
6
5
 1 2 0
  2 −4 6 
2 0 = 
 ⋅  3 −4 −4
  −3 6 −9 
4 −4
1 −1
 2
daraus folgt mit dem Distributivgesetz für die Matrizenmultiplikation
0

5

1
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
33
1 −3 5  1 2 0
 
3 2 0 −  3 −4 −4
 
6 4 −4  2
1 −1
 3
 2 −4 6 
4

⋅
 −3 6 −9 
 2
0 
   0 0 0
5  = 

   0 0 0
1 
oder
 2 −1 −3 5
 2 −4 6 
  0 0 0

 ⋅  1 7 6 −5 = 

 −3 6 −9 
  0 0 0
 0 5 5 −5
Dieses Beispiel zeigt, dass es nicht möglich ist, generell eine Division für Matrizen zu erklären, denn dann könnten wir in der Gleichung
 3
 2 −4 6 

⋅ 4
 −3 6 −9 
 2
1 −3
3
6
5
 1 2 0
  2 −4 6 
2 0 = 
 ⋅  3 −4 −4
  −3 6 −9 
4 −4
1 −1
 2
0

5

1
durch die von der Nullmatrix verschiedene Matrix
 2 −4 6


 −3 6 −9
dividieren, was offensichtlich zu einem Widerspruch führen würde.
3.1
Die inverse Matrix
Wir betrachten zunächst das lineare Gleichungssystem
x 1 + 3x 2 = a 1
2x 1 + 7 x 2 = a 2
a1, a2 ∈ R gegeben. In Matrizenschreibweise lässt sich das Gleichungssystem mit Einführung
von
 1 3
,
A = 
 2 7
x 
a 
x =  1 , a =  1 
x2 
a2 
in der Form
A⋅x = a
schreiben. Die Lösung lautet:
34
x 1 = 7a 1 − 3a 2
x 2 = −2a 1 + a 2
die mit
 7 − 3

X = 
1
− 2
die Gestalt
x = X⋅a
annimmt. Also haben wir einerseits
A⋅x = A⋅X⋅a = a
und andererseits
x = X⋅a = X⋅A⋅x
so dass offenbar A ⋅ X das a und X ⋅ A das x beim Multiplizieren reproduziert. Durch Ausrechnen bestätigen wir sofort:
 1 0

A ⋅ X = X ⋅ A = I = 
 0 1
Definition 3-16
Die quadratische m × m Matrix X mit der Eigenschaft X ⋅ A = A ⋅ X = I heißt inverse Matrix
von A. Dabei ist A eine reguläre m × m Matrix und I die m × m Einheitsmatrix.
Wir schreiben:
X = A −1
Definition 3-17
Die Inverse A-1 der Matrix A kann aus der Definitionsgleichung
A ⋅ A −1 = A −1 ⋅ A = I
berechnet werden.
Beispiel 3-2
Für n = 3 und X = A-1 gilt:
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
 a 11

 a 21
a
 31
a 12
a 22
a 32
35
a 13   x 11
 
a 23  ⋅  x 21
a 33   x 31
x 12
x 22
x 32
x 13   1 0 0 
 

x 23  =  0 1 0 
x 33   0 0 1 
Der obigen Gleichung entsprechen 3 lineare Gleichungssysteme zur Bestimmung der Koeffizienten xij von A-1:
a 11 x 11 + a 12 x 21 + a 13 x 31 = 1
a 11 x 12 + a 12 x 22 + a 13 x 32 = 0
a 11x 13 + a 12 x 23 + a 13 x 33 = 0
a 21x 11 + a 22 x 21 + a 23 x 31 = 0 a 21x 12 + a 22 x 22 + a 23 x 32 = 1
a 21 x 13 + a 22 c 23 + a 23 x 33 = 0
a 31 x 11 + a 32 x 21 + a 33 x 31 = 0 a 31 x 12 + a 32 x 22 + a 33 x 32 = 0 a 31x 13 + a 32 x 23 + a 33 x 33 = 1
Satz 3-5
Die Inverse einer oberen (unteren) Dreiecksmatrix ist wieder eine obere (untere) Dreiecksmatrix.
Beispiel 3-3 (obere Dreiecksmatrix, n = 3):
Aus der obigen Gleichung folgt
a 11 x 11 + a 12 x 21 + a 13 x 31 = 1 a 11x 12 + a 12 x 22 + a 13 x 32 = 0 a 11 x13 + a 12 x 23 + a 13 x 33 = 0
a 22 x 21 + a 23 x 31 = 0
a 22 x 22 + a 23 x 32 = 1
a 22 x 23 + a 23 x 33 = 0
a 33 x 31 = 0
a 33 x 32 = 0
a 33 x 33 = 1
und durch rekursive Auflösung
x 31 = 0
x 32 = 0
x 21 = 0
x 22 =
x 23
x 12
x 13
x 11 =
1
a 11
1
a 22
a
= − 12 x 22
a 11
also
A −1
 x 11

= 0
 0

1
a 33
a
= − 23 x 33
a 22
1
(a 13 x 33 + a 12 x 23 )
=−
a 11
x 33 =
x 12
x 22
0
x 13 

x 23 
x 33 
36
Besonders einfach ist die Invertierung einer Diagonalmatrix. Aus
 a 11

A= 0
 0

0
a 22
0
0 

0 
a 33 
A −1
folgt
 1

 a 11

= 0

 0


0
1
a 22
0

0 


0 

1 
a 33 
Satz 3-6
Es gilt:
a) (A T ) = (A −1 )
b) (A −1 ) = A
d) (λA ) =
e) A −1 =
−1
−1
−1
T
1 −1
A ,λ ≠ 0
λ
c) (A ⋅ B) −1 = B −1 ⋅ A −1
1
A
Satz 3-7
Die inverse Matrix A-1 einer regulären m × m Matrix A berechnet sich folgendermaßen:
A
−1
 + A 11

 − A12
1 
=
+ A 13
A


1+ m
 (− 1) A 1m
− A 21
+ A 31
+ A 22
− A 32
− A 23
+ A 33
(− 1)m+1 A11 
(− 1)m + 2 A11 
(− 1)m+3 A11 
A mm



Satz 3-8
Eine quadratische m × m Matrix A besitzt dann und nur dann eine Inverse, wenn
a) ihre Determinante von Null verschieden ist,
b) der Rang von A gleich m ist,
c) A regulär ist,
d) die Spalten und Zeilen von A eine Basis im Rn bilden.
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
37
4 Determinanten
Definition 4-1
Eine n-reihige Determinante1 ist eine Zahl, die aus gegebenen n2 Zahlen aik nach einer noch
zu bestimmenden Vorschrift gebildet wird.
D = det(a ik ) = a ik
a 11
a 21
=
a a i1
a n1
a 12
a 22
a i2
a n2
a 1k
a 2k
a ik
a nk
a 1n
a 2n
a in
a nn
Zeilen und Spalten heißen allgemein Reihen.
Definition 4-2 (Rechenvorschrift zur Bestimmung der Determinante)
Im Fall n = 1 wird
det(a 11 ) = a 11 = a 11
Für die Fälle n = 2, 3, 4,... wird der Begriff der n-reihigen Determinante durch die Vorschrift
a 11
a 21
a 12
a 22
a n1
a n2
a 1n
a 22
a 2n
a
= a 11 ⋅ 32
a nn
a n2
a 21
a
+ a 13 ⋅ 31
a n1
a 22
a 32
a n2
a 24
a 34
a n4
a 23 a 2 n
a 21
a 33 a 3n
a
− a 12 ⋅ 31
a n 3 a nn
a n1
a 23
a 33
a n3
a 24
a 34
a n4
a 2n
a 3n
+
a nn
a 2n
a 3n
− + + (−1) n +1 a 1n
a nn
a 21
a 31
⋅
a n1
a 22
a 32
a n2
a 2,n −1
a 3, n −1
a n ,n −1
auf den Begriff der (n-1)-reihigen Determinante oder auch Unterdeterminante zurückgeführt.
1
Gottfried Wilhelm Leibniz, deutsch. Mathematiker und Philosoph, 1646-1716
38
Beispiel 4-1 (n = 2):
a b
= a ⋅ d − b ⋅ c = ad − bc
c d
Definition 4-3
Entfernen wir aus dem Zahlenschema |aik| die i-te Zeile und die k-te Spalte und rücken die
verbleibenden Elemente wieder zu einer Determinante zusammen, so entsteht die zum Element aik gehörige Unterdeterminante Dik. Sie ist von der Ordnung n-1.
Beispiel 4-2 (n = 3):
a11
a12
a 21 a 22
a 31 a 32
a13
a 23 ⇒
a 33
D 21 =
a12
a 32
a13
a 33
Aus den n2 Elementen einer n-reihigen Determinante lassen sich n2 Unterdeterminanten der
Ordnung n-1 bilden.
Definition 4-4
Unter dem Rang einer Matrix versteht man die höchste Ordnung, die deren nicht verschwindende Unterdeterminanten haben können.
Hinweis: Um den Rang einer Matrix zu bestimmen, sind alle Unterdeterminanten der Ordnung l zu betrachten, wobei l entweder die kleinere der beiden Zahlen m und n für m ≠ n
oder l = m = n ist. Ist wenigstens eine dieser Determinanten ≠ 0 , so ist der Rang der Matrix A
gleich l. Verschwinden sie jedoch alle, dann sind die Unterdeterminanten l - 1 zu betrachten
usw. In der praktischen Anwendung ist es jedoch besser, umgekehrt zu verfahren, d.h., von
Unterdeterminanten geringerer Ordnung zu denen höherer Ordnung überzugehen, und dabei
folgende Regel zu beachten: Hat man eine nichtverschwindende Unterdeterminante k-ter Ordnung gefunden, so sind nur noch die Unterdeterminanten der Ordnung (k + 1) zu betrachten,
sich durch Ränderung von Dk ergeben
Dk … …
Dk
… …
… …
Dk Dk
Sind dann alle diese Unterdeterminanten der Ordnung (k + 1) gleich Null, dann ist der Rang
der Matrix gleich k.
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
39
Beispiel 4-3
Gesucht wird der Rang der Matrix
3
1 0
2 − 4


1 − 4 2
1 −2
A=
0
1 −1
3 1


4 − 7

4
−
4
5


Die Matrix A enthält in der oberen linken Ecke eine Unterdeterminante zweiter Ordnung
D2 =
2 −4
= 0 . Es existiert jedoch eine Unterdeterminante zweiter Ordnung, die nicht ver1 −2
′ −4 3
= 2 ≠ 0 . Rändern dieser Unterdeterminante links und unten liefert:
schwindet: D 2 =
−2 1
2 −4
3
D3 = 1 − 2
1 = 1 ≠ 0 . Durch Rändern von D3 erhalten wir1
0
1 −1
2 −4
3
1
1 −2
1 −4
D4 =
=0
0
1 −1
3
4 −7
4 −4
und
2 −4
3
1
′ 1 −2
D4 =
0
1 −1
4 −7
4
0
2
=0
1
5
Somit ist der Rang von A gleich 3
Definition 4-5
Es existieren 2n Möglichkeiten zur Berechnung einer n-reihigen Determinante. Entwicklung
nach den Elementen der i-ten Zeile (= n Möglichkeiten)
n
D = ∑ (−1) i + k a ik D ik
1≤ i ≤ n
k =1
Entwicklung nach den Elementen der k-ten Spalte (= n Möglichkeiten)
n
D = ∑ (−1) i + k a ik D ik
i =1
1
das ist nur auf zwei verschiedene Arten möglich
1≤ k ≤ n
40
Beispiel 4-4 (n = 3): Entwicklung nach der ersten Zeile
a 11
D = a 21
a 31
a 12
a 22
a 32
a 13
a
a 23 = a 11 ⋅ 22
a 32
a 33
a 23
a
− a 12 ⋅ 21
a 33
a 31
a 23
a
+ a 13 ⋅ 21
a 33
a 31
a 22
a 32
= a 11a 22 a 33 − a 11a 23 a 32 − a 12 a 21a 33 + a 12 a 23 a 31 + a 13 a 21a 32 − a 13 a 22 a 31
+ − + −
− + − +
+ − + −
Schachbrettregel für das Vorzeichen:
− + − +
Hinweis: In den folgenden Sätzen kann das Wort Reihe sowohl durch das Wort Zeile als auch
durch das Wort Spalte ersetzt werden.
Satz 4-1
Eine Determinante ändert ihren Wert nicht bei Vertauschung ihrer Zeilen mit ihren Spalten
(Spiegelung an der Hauptdiagonalen)
a 11
a 12
a 13
a 11
a 21
a 31
a 21
a 31
a 22
a 32
a 23 = a 12
a 33 a 13
a 22
a 23
a 32
a 33
Satz 4-2
Eine Determinante ändert ihr Vorzeichen bei Vertauschung zweier paralleler Reihen.
a 11
a 12
a 13
a 11
a 12
a 13
a 21
a 31
a 22
a 32
a 23 = − a 31
a 33
a 21
a 32
a 22
a 33
a 23
Satz 4-3
Wenn die Elemente der k-ten Reihe einer Determinante D Summen von zwei Summanden
sind, so lässt sich D als Summe zweier Determinanten darstellen, deren Elemente in der ent-
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
41
sprechenden k-ten Reihe jene Summanden sind und in den übrigen Reihen mit D übereinstimmen.
c11
c 21
c 31
c 41
c12
c 22
c 32
c 42
a 1 + b1
a 2 + b2
a 3 + b3
a 4 + b4
c14
c11
c 24
c
= 21
c 34
c 31
c 44
c 41
c12
c 22
c 32
c 42
a1
a2
a3
a4
c14 c11
c 24 c 21
+
c 34 c 31
c 44 c 41
c12
c 22
c 32
c 42
b1
b2
b3
b4
c14
c 24
c 34
c 44
Satz 4-4
Ein den Elementen einer Reihe gemeinsamer Faktor darf vor die Determinante gezogen werden.
a 11
λa 12
a 13
a 11
a 12
a 13
a 21
a 31
λa 22
λa 32
a 23 = λ ⋅ a 21
a 33
a 31
a 22
a 32
a 23
a 33
Satz 4-5
Sind die Elemente einer Reihe lauter Nullen, so hat die Determinante den Wert Null.
a 11
a 12
a 13
0
a 31
0
a 32
0 =0
a 33
Satz 4-6
Sind die Elemente zweier paralleler Reihen zueinander proportional, oder stimmen zwei Reihen überein, so hat die Determinante den Wert Null.
a 11
λa 11
a 13
a 11
a 12
a 13
a 21
a 31
λa 21
λa 31
a 23 = 0
a 33
a 21
a 21
a 22
a 22
a 23 = 0
a 23
Satz 4-7
Sind A und B beliebige quadratische n-reihige Matrizen, so gilt:
A⋅B = A B
Beispiel 4-5
Berechnung der Determinante einer oberen Dreiecksmatrix
42
a 11
a 12
0
0
a 22
0
a 13
a
a 23 = a 11 22
0
a 33
a 23
= a 11a 22 a 33 = a 11a 22 a 33
a 33
Satz 4-8
Besitzt eine n-reihige Determinante obere oder untere Dreiecksgestalt, so errechnet sich die
Determinante aus dem Produkt der Hauptdiagonalglieder:
n
D = det(a ik ) = ∏ a ii
i =1
5 Lineare Gleichungssysteme
Definition 5-1
Unter einem linearen Gleichungssystem (LGS) verstehen wir m lineare Gleichungen, in denen n Unbekannte x1, x2, x3,..., xn auftreten. Hierbei sind die Koeffizienten a ij (i = 1...m, j =
1...n) und die Absolutglieder der rechten Seite b i = i = 1,…, m gegeben.
a 11 x 1 + a 12 x 2 + … + a 1n x n = b1
a 12 x 1 + a 22 x 2 + … + a 2 n x n = b 2
a m1 x 1 + a m 2 x 2 + … + a mn x n = b m
Mit den Vektoren
 a 11 
 a 1n 
 b1 




 
a 1 =  ,… , a n =  , … , b =  
a 
a 
b 
 m1 
 mn 
 m
erhalten wir die vektorielle Darstellung des LGS
a1x1 + a 2 x 2 + … + a n x n = b
 a 11

a
Mit A = (a 1 ,… , a n ) =  21

a
 m1
a 12 a 1n 
 x1 

 
a 22 a 2 n 
x 
und x =  2 


 
x 
a m 2 a mn 
 m
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
43
folgt die Matrixdarstellung des LGS
A⋅x = b
Ein LGS heißt homogen, wenn b1 = b 2 = … = b m = 0 sind. Andernfalls heißt es inhomogen.
Beispiel 5-1 (Inhomogenes LGS mit 3 Gleichungen für 3 Unbekannte x1, x2, x3)
4x 1
2x 1
x1
+ 3x 2
− x2
+ 2x 2
− x3
+
x3
− 2x 3
= −1
=
5
= −5
mit
3 − 1
4


A =  2 −1
1;
 1 2 − 2


 x1 
 
x =  x 2 ;
x 
 3
 b1   − 1
   
b =  b 2  =  5 .
 b   − 5
 3  
Definition 5-2
Ein Zahlentupel ( x̂ 1 , x̂ 2 , … , x̂ n ) ∈ R n , welches alle m Gleichungen des LGS erfüllt, heißt
Lösung des LGS. Die Menge aller Lösungen heißt Lösungsmenge des LGS.
Satz 5-1
Bei homogenen LGS ist jedes Vielfache der Lösung wieder eine Lösung.
Satz 5-2
Ein inhomogenes LGS von n Gleichungen mit n Unbekannten besitzt bei regulärer Koeffizientenmatrix genau eine Lösung.
Satz 5-3
Ein homogenes LGS von n Gleichungen mit n Unbekannten besitzt bei regulärer Koeffizientenmatrix nur die triviale Lösung x 1 = x 2 = … = x n = 0 .
44
Satz 5-4 (Die Cramersche Regel)
Gegeben sei ein inhomogenes LGS von n Gleichungen mit n Unbekannten mit einer regulärer
Koeffizientenmatrix in der vektoriellen Darstellung
a1x1 + a 2 x 2 + … + a n x n = b ,
dann hat der Lösungsvektor die Komponenten
xk =
a 1 ,… , a k −1 , b, a k +1 ,… , a n
a 1 , a 2 , … , a k ,… , a n
=
Ak
A
k = 1,2, …, n.
,
wobei |A| die Determinante von A und |Ak| diejenige Determinante ist, die aus A entsteht,
wenn wir in A die k-te Spalte durch die Spalte der rechten Seite ersetzten1.
4x 1
2x 1
x1
−1
D1 =
3
+ 3x 2
− x2
+ 2x 2
−1
4
5 −1
1 = 10
−5 2 −2
4
3
−1
= −1
5
=
= −5
−1
−1
D2 = 2
5
1 = −10
1 −5 −2
4
D3 = 2 − 1
5 = 20
1 2 −5
x1 =
− x3
x3
+
− 2x 3
3
−1
D = 2 −1
1 = 10
1 2 −2
D
D1 10
D
20
− 10
=
= 1; x 2 = 2 =
= −1; x 3 = 3 =
=2
D 10
D
10
D 10
Definition 5-3
Zwei Gleichungssysteme heißen äquivalent, wenn sie die gleiche Lösungsmenge besitzen.
1
Gabriel Cramer, schweizer. Mathematiker, 1704-1752
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
45
Satz 5-5
Zwei LGS sind genau dann äquivalent, wenn sie sich durch
a) Vertauschen zweier Gleichungen (Zeilen) miteinander,
b) Multiplikation einer Gleichung (Zeile) mit einer reellen Zahl α ≠ 0 ,
c) Addition des Vielfachen einer Gleichung (Zeile) zu einer anderen Gleichung (Zeile)
ineinander überführen lassen.
Gaußscher Algorithmus
Ein LGS wird durch äquivalente Umformungen auf Dreiecksgestalt gebracht. Dieses äquivalente Gleichungssystem lässt sich rekursiv lösen.
Satz 5-6
Ein homogenes LGS von n Gleichungen mit n Unbekannten besitzt genau dann nichttriviale
Lösungen, wenn der Rang r der Koeffizientenmatrix kleiner als n ist. Die Lösungsmenge enthält n-r freie Parameter. Sie hat die Dimension n-r.
Satz 5-7
Ein inhomogenes LGS von n Gleichungen mit n Unbekannten und Rang von A gleich r < n
besitzt nur dann Lösungen, wenn der Rang von ( A b ) auch gleich r ist.
Satz 5-8
Ein LGS mit m Gleichungen und n Unbekannten hat genau dann mindestens eine Lösung,
wenn der Rang der Koeffizientenmatrix A und der Rang der erweiterten Matrix ( A b ) übereinstimmen.
Definition 5-4
Für ein homogenes LGS von n Gleichungen mit n Unbekannten heißt jede Zahl λi, für die die
Gleichung
(A − λE ) ⋅ x = 0
nichttriviale Lösungen besitzt, Eigenwert von A. Notwendige Bedingung dafür ist
46
A − λE = 0 ,
oder:
a 11 − λ
a 12
a 21
a 22 − λ
a n1
a n2
a 1n
a 2n
=0
a nn − λ
Die nichttrivialen Lösungen x des homogenen Gleichungssystems (A − λE ) ⋅ x = 0 können bei
bekannten Eigenwerten λ i (i = 1, n) berechnet werden. Sie werden Eigenvektoren xi der
Matrix A zum Eigenwert λ i genannt. Der k-te Eigenvektor genügt der Gleichung
(A − λ k E ) ⋅ x k
=0
Beispiel 5-2 (n = 3)
a 11 − λ a 12
a 13
a 22 − λ a 23
=0
a 32
a 33 − λ
a 21
a 31
Ausmultiplizieren führt auf die charakteristische Gleichung von A:
λ3 − A1 λ2 + A 2 λ − A 3 = 0
mit den Invarianten
3
A 1 = ∑ a kk ;
k =1
A2 =
1 3
∑ (a jj a kk − a jk a kj );
2 j,k =1
A3 = A
Beispiel 5-3 (n = 2)
a 11 − λ a 12
=0
a 21
a 22 − λ
Ausmultiplizieren liefert die quadratische Gleichung:
λ2 − (a 11 + a 22 )λ + (a 11a 22 − a 21a 12 ) = 0
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
47
Satz 5-9
Die Eigenwerte einer symmetrischen Matrix A (A = AT) sind reell.
Beispiel 5-4
 3 2

Gesucht sind die Eigenwerte der symmetrischen Matrix A = 
 2 3
Das charakteristische Polynom:
λ2 − 6λ + 5 = 0
hat die Lösungen: λ 1 = 1; λ 2 = 5 . Das sind die Eigenwerte von A.
Beispiel 5-5
 3 2
 .
Gesucht sind die Eigenvektoren der Matrix A = 
 2 3
Die Eigenwerte sind λ 1 = 1; λ 2 = 5 . Für den ersten Eigenwert λ1 = 1 ergibt sich folgendes
Gleichungssystem
 3 2 
 1 0   x 1 
 ⋅   = 0
 − λ 1 

 0 1   x 2 
 2 3 
 3 − 1 2   x1 
 ⋅   = 0

 2 3 − 1  x 2 
also
2x 1 + 2x 2 = 0
2x 1 + 2x 2 = 0
 1
Wir wählen x 1 = t ∈ Ñ, dann folgt x 2 = − t . Damit ist jeder Vektor x 1 = t  Eigenvektor
 − 1
zu λ1 = 1 . Für den zweiten Eigenwert λ 2 = 5 erhalten wir entsprechend
 3 2 
 1 0   x 1 
 ⋅   = 0
 − λ 2 

 0 1   x 2 
 2 3 
2   x1 
3 − 5
⋅  = 0

3 − 5   x 2 
 2
also
− 2x 1 + 2x 2 = 0
2x 1 − 2x 2 = 0
48
1
Mit x 1 = s beliebig reell folgt x 2 = s . Damit ist jeder Vektor x 2 = s  Eigenvektor zu
1
λ 2 = 5 . Die auf den Betrag 1 normierten Eigenvektoren sind:
e1 =
1 1
1  1
 ; e 2 =
 
2 1
2  − 1
Satz 5-10
Die Eigenvektoren einer symmetrischen Matrix sind orthogonal.
Definition 5-5
Die n unabhängigen Eigenvektoren xi lassen sich in folgender Reihenfolge zu der regulären
Matrix
X = (e1 , e 2 ,…, e n ) ,
die Eigenvektormatrix oder auch Modalmatrix genannt wird, zusammenfassen.
Definition 5-6
Für die Modalmatrix gilt:
X −1 ⋅ A ⋅ X = Λ , wobei
…
 λ1 0

 0 λ2 …
Λ=
… … λ n −1

0 0
0

0

0
= Diag(λ ii )
0

λ n 
Diagonalmatrix der Eigenwerte genannt wird.
1

 3 2
1  1 1
1 1
1  1
; X −1 = 2 2
 ; e1 =
 ; e 2 =
  ; X = 
A = 
2  − 1 1
2 1
2  − 1
 1
 2 3
2
 1 0   λ1
 = 
X −1 ⋅ A ⋅ X = Λ = 
 0 5  0
0

λ 2 
1
−  1 − 1
2 =
;
1  1 1

2
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
49
6 Analysis
Definition 6-1
Unter einer Funktion f verstehen wir eine Vorschrift, die jedem Element x einer gegebenen
Menge D genau ein Element y aus einer Menge W zuordnet. D heißt Definitionsbereich und
W heißt Wertebereich. Schreibweise:
f : D → W mit y = f ( x )
Definition 6-2
Es sei f : D → W eine Funktion.
a) f ist geradsymmetrisch, wenn f(-x) = f(x) für alle x ∈ D gilt.
b) f ist ungeradsymmetrisch (punktsymmetrisch zum Ursprung), wenn f(-x) = -f(x) für alle
x ∈ D gilt.
Definition 6-3
Es ist I ⊆ Ñ ein Intervall. Eine Funktion f: I → W heißt
a) monoton wachsend in I, wenn für alle x1 < x2 aus I gilt, daß f(x1) ≤ f(x2) ist
b) streng monoton wachsend in I, wenn für alle x1 < x2 aus I gilt, daß f(x1) < f(x2) ist,
c) monoton fallend in I, wenn für alle x1 < x2 aus I gilt, daß f(x1) ≥ f(x2) ist,
d) streng monoton fallend in I, wenn für alle x1 < x2 aus I gilt, daß f(x1) > f(x2) ist.
Definition 6-4
Es ist I ⊆ Ñ ein Intervall. Eine Funktion f: I → W heißt
a) konvex in I, wenn ihr Graph mit größer werdenden x-Werten eine Linkskurve beschreibt,
b) konkav in I, wenn ihr Graph mit größer werdenden x-Werten eine Rechtskurve beschreibt
Definition 6-5
Die Umkehrfunktion (inverse Funktion) f
−1
W das Element x des Definitionsbereiches D zu.
ordnet jedem Element f(x) des Wertebereiches
50
Satz 6-1
Jede streng monotone Funktion besitzt ein Umkehrfunktion
Definition 6-6
Eine Funktion der Form
f (x) = a 0 + a 1x + a 2 x 2 + … + a n x n ,
an ≠ 0,
mit ai ∈ Ñ, i = 0,1, … , n , fest, heißt ganze rationale Funktion oder Polynom vom
Gerade n.
Satz 6-2
Ein Polynom n-ten Grades hat genau n Nullstellen, d.h. Lösungen der Gleichung f ( x ) = 0 .
Ist n ungerade, dann gibt es mindestens eine reelle Nullstelle.
Definition 6-7
Ist g(x) ein Polynom vom Grade n und h(x) ein Polynom vom Grade m > 0, dann heißt die
Funktion
f (x) =
a 0 + a 1x + a 2 x 2 + … + a n x n
g( x )
=
2
m
h (x )
b 0 + b1 x + b 2 x + … + b m x
eine gebrochen rationale Funktion.
Satz 6-3
Der größtmögliche Definitionsbereich einer gebrochen rationalen Funktion ist
Dmax = R\{x|h(x) = 0}
Definition 6-8
Nullstellen des Nenners einer gebrochen rationalen Funktion, die nicht gleichzeitig Nullstellen
des Zählers sind, heißen Pole.
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
51
Definition 6-9
Die Funktion f ( x ) = e x heißt Exponentialfunktion. Sie ist auf
definiert und
e = 2,718281... ist die Eulersche Zahl.
Definition 6-10
Die Umkehrfunktion von e x wird mit f ( x ) = ln x bezeichnet. Sie heißt (natürliche) Logarithmusfunktion und ist für x > 0 definiert.
Satz 6-4
Es sei x 1 ∈ (0, ∞ ), x 2 ∈ (0, ∞ ), x ∈ (0, ∞ ) und a ∈
, dann gilt:
a) ln(x 1 x 2 ) = ln x 1 + ln x 2
x 
b) ln 1  = ln x 1 − ln x 2
 x2 
c) ln(x a ) = a ln x
Definition 6-11
Der Sinus eines Winkels x wird am rechtwinkligen Dreieck erklärt als das Verhältnis von
Gegenkathete zu Hypothenuse . Der Cosinus von x ist das Verhältnis von Ankathete zu Hypothenuse
sin x =
g
h
cos x =
a
h
Am Einheitskreis werden diese Funktionen auf beliebige (im Bogenmaß gemessene) Winkel
ausgedehnt.
52
Beide Funktionen haben die Periode 2 π . Der Definitionsbereich ist Ñ und der Wertebereich
ist [-1,1]. Es gilt:
a) sin( − x ) = − sin x
b) cos(− x ) = cos( x )
c) sin 2 x + cos 2 x = 1
π

d) cos x −  = sin x
2

Definition 6-12
tan x =
sin x
cos x
1

für alle x ≠  k + π , cot x =
für alle x ≠ kπ ,
cos x
sin x
2

6.1
Grenzwert und Stetigkeit von Funktionen
k = … − 1,0,1…
Definition 6-1
Gegeben ist eine Funktion f : D → W . Wenn bei der Annäherung von x gegen x0 die Funktionswerte einem Wert g beliebig nahe kommen, dann heißt g der Grenzwert von y = f ( x )
für x gegen x0 . Wir schreiben dann lim f ( x ) = g .
x → x0
Definition 6-2
f ( x ) hat für x → ∞ (x → −∞ ) den Grenzwert G, wenn es für jedes ε > 0 einen Wert x ε
gibt, so daß für alle x > x ε (x < x ε ) gilt, daß f ( x ) − G < ε ist.
Definition 6-3
f(x) hat den Grenzwert g an der Stelle x0 , wenn zu jedem ε > 0 ein δ ε derart existiert, daß
f ( x ) − g < ε für alle x mit x − x 0 < δ ε erfüllt ist.
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
53
Definition 6-4
Es sei f : D → W eine Funktion und x 0 ∈ D . Die Funktion f heißt stetig in x0, wenn
a) lim f ( x ) existiert und
x →x 0
b) lim f ( x ) = f (x 0 ) ist.
x→x 0
Die Funktion heißt stetig in D, wenn sie für alle x 0 ∈ D stetig ist.
Satz 6-1
Für die elementaren Funktionen gilt:
-
Polynome sind stetig,
-
ex und ln x sind stetig,
-
sin x und cos x sind stetig,
-
gebrochen rationale Funktionen sind stetig für alle x, für die das Nennerpolynom nicht
verschwindet.
Satz 6-2
Es sei die Funktion f :[a , b] → W stetig und es sei f ( a ) > 0 und f ( b) < 0 [oder f ( a ) < 0
und f ( b) > 0 ], dann existiert mindestens ein x0 ∈ ( a , b) mit f ( x0 ) = 0 .
6.2
Ableitung von Funktionen einer unabhängigen Veränderli-
chen
Definition 6-1
Sei I ∈
ein Intervall und x0 ∈ I : Als Differenzenquotient von f bezeichnen wir den Aus-
druck
f (x ) − f (x 0 )
für x ≠ x 0
x − x0
Definition 6-2
Sei I ∈ Ñ ein Intervall und x0 ∈ I . Die Funktion f heißt differenzierbar in x0, wenn der
Grenzwert
lim
x →x 0
f (x ) − f (x 0 )
x − x0
54
existiert. Dieser Grenzwert wird mit f ′( x0 ) bezeichnet und heißt Ableitung oder Differentialquotient von f in x0. f heißt differenzierbar, falls f ′( x0 ) für alle x0 ∈ I existiert.
Ableitungen spezieller Funktionen
f ( x)
f ′( x )
f ( x)
f ′( x )
a = konst .
0
xα
ex
ex
ln x
sin x
cos x
tan x
cos x
− sin x
cot x
αx α −1
1
x
1
cos 2 x
1
−
sin 2 x
1
1 + x2
1
−
1 + x2
1
cosh 2 x
1
−
sinh 2 x
1
1 − x2
1
1 − x2
1
arcsin x
arccos x
−
1 − x2
1
1 − x2
arctan x
arc cot x
sinh x
cosh x
tanh x
cosh x
sinh x
coth x
ar sinh x
ar cosh x
1
x +1
1
2
x2 − 1
ar tanh x
ar coth x
Satz 6-1
Es sei f : D → Wf und g : D → Wg . Existieren die Ableitungen f ′(x ) und g′(x ) für alle x aus
D, dann sind auch kf mit k ∈ Ñ, f ± g , fg und
′
a) [kf (x )] = kf ′(x )
′
b) [f (x ) ± g(x )] = f ′(x ) ± g ′(x )
′
c) [f (x )g (x )] = f ′(x )g (x ) + f (x )g ′(x )
′
 f (x )  f ′(x )g(x ) − f (x )g ′(x )
d) 
 =
[g(x )]2
 g(x ) 
f
(für g ≠ 0 ) differenzierbar und es gilt:
g
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
55
Satz 6-2
Sind f(x) und g(x) differenzierbar und kann g(x) in f(x) eingesetzt werden, dann ist auch f(g(x))
differenzierbar und es gilt
[f (g( x) )]′ = f ′(g(x ) ) g ′(x )
Satz 6-3
Für die Ableitung der Umkehrfunktion f −1 an der Stelle y 0 = f (x 0 ) gilt
(f )′ (y ) = f ′(1x )
−1
0
0
Satz 6-4
Ist f differenzierbar in x0, dann ist f auch stetig in x0 .
Definition 6-3
′
Ist f ′( x ) differenzierbar, dann heißt die Ableitung von f ′ : [f ′(x )] = f ′′(x ) zweite Ableitung
von f. Allgemein läßt sich schreiben
[f (
n −1)
(x )]′ = f (n ) (x ),
n = 2,3, …
Satz 6-5
Es sei D ⊆
und f : D → W eine Funktion. Es sei I ⊆ D ein Intervall und f differenzierbar
auf I. Dann gilt:
a) f ist genau dann monoton wachsend auf I, wenn für alle x ∈ I f ′( x ) ≥ 0 ist.
b) f ist genau dann monoton fallend auf I, wenn für alle x ∈ I f ′( x ) ≤ 0 ist.
c) Ist f ′( x ) > 0 für alle x ∈ I bis auf endlich viele x, dann ist f streng monoton wachsend
auf I.
d) Ist f ′( x ) < 0 für alle x ∈ I bis auf endlich viele x, dann ist f streng monoton fallend auf
I.
Satz 6-6
Es sei D ⊆
und f : D → W eine Funktion. Es sei I ⊆ D ein Intervall und f zweimal diffe-
renzierbar auf I. Dann gilt:
a) f ist genau dann konvex auf I, wenn f ′′( x ) > 0 für alle x ∈ I (Linkskurve).
b) f ist genau dann konkav auf I, wenn f ′′( x ) < 0 für alle x ∈ I (Rechtskurve).
56
6.3
Spezielle Anwendungen der Differentialrechnung
Definition 6-1
Unter dem (totalen, vollständigen) Differential einer differenzierbaren Funktion f : D → W
verstehen wir die Größe dy = f ′( x ) dx für beliebige Zahlen (Zuwächse) dx.
Abb. 6-1 Linearer Zuwachs dy einer Funktion y(x)
Satz 6-1
Es sei D ⊆
(Regel von Bernoulli-L’Hospital)
ein Intervall und x0 ∈ D . Es seien f , g : D \ {x0 } → W differenzierbare Funk-
tionen. Es gelte: lim f ( x ) = 0 , lim g( x ) = 0 , oder lim f ( x ) = ±∞ , lim g( x ) = ±∞ .
x → x0
x → x0
x → x0
x → x0
Ferner sei g ′( x ) ≠ 0 für x ∈ D . Existiert dann der Grenzwert von
existiert auch der Grenzwert von
f ( x)
für x → x0 und es ist
g( x )
f (x )
f ′(x )
= lim
x → x 0 g (x )
x → x 0 g ′(x )
lim
f ′( x )
für x → x0 , dann
g ′( x )
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
6.4
57
Extremwerte bei Funktionen einer Veränderlichen
Definition 6-1
Es sei D ⊆
und f : D → W eine Funktion. Ein Punkt x0 ∈ D heißt lokales (relatives)
Maximum (Hochpunkt) von f [lokales(relatives)Minimum(Tiefpunkt) von f], wenn es eine
Zahl h > 0 gibt mit
f ( x ) ≤ f ( x0 ) für alle x ∈ D mit x0 − h < x < x0 + h
[ f ( x ) ≥ f ( x0 ) für alle x ∈ D mit x0 − h < x < x0 + h ]
Satz 6-1
Es sei f : D → W eine Funktion, die an einer inneren Stelle x0 ∈ D differenzierbar ist. Wenn
f in x0 einen Extremwert besitzt, dann gilt f ′( x0 ) = 0 . (Notwendige Bedingung für ein Extremum)
Definition 6-2
Es sei f : D → W eine differenzierbare Funktion, dann heißt jede Lösung der Gleichung
f ′( x ) = 0
stationärer Punkt der Funktion f.
Satz 6-2
Es sei f : D → W eine differenzierbare Funktion.
a) (Notwendige Bedingung für einen inneren Extremwert)
Ist x0 ein innerer Extremwert, dann gilt f ′( x0 ) = 0
b) (Hinreichende Bedingung für Hoch- oder Tiefpunkt)
(i)
Es gilt f ′( x0 ) = 0 und mit h > 0 gilt weiter
f ′( x ) > 0 für x0 − h < x < x0 und
f ′( x ) < 0 für x0 < x < x0 + h
dann hat f am Punkte x0 einen Hochpunkt.
(ii)
Es gilt f ′( x0 ) = 0 und mit h > 0 gilt weiter
58
f ′( x ) < 0 für x0 − h < x < x0 und
f ′( x ) > 0 für x0 < x < x0 + h
dann hat f am Punkte x0 einen Tiefpunkt.
c) (Hinreichende Bedingung für Hoch- oder Tiefpunkt)
Gilt f ′( x0 ) = 0 und f ′′( x0 ) ≠ 0 , dann hat f an der Stelle x0
(i)
einen Hochpunkt (Maximum), wenn f ′′( x0 ) < 0
(ii)
einen Tiefpunkt (Minimum), wenn f ′′( x0 ) > 0 ist.
Satz 6-3
Ist f : D → W eine differenzierbare Funktion, die in D konkav (konvex) verläuft, und die einen inneren Punkt x0 ∈ D mit f ′( x0 ) = 0 hat, dann besitzt f in x0 ein globales Maximum
(Minimum).
Definition 6-3
Ein Punkt, in dem eine Rechts- und eine Linkskurve (oder eine Links- und eine Rechtskurve)
ohne Knick ineinander übergehen, heißt Wendepunkt.
Satz 6-4
Es sei f : D → W eine mindestens dreimal differenzierbare Funktion. Gilt für einen inneren
Punkt x0 ∈ D f ′′( x0 ) = 0 und f ′′′( x0 ) ≠ 0 , so ist x0 ein Wendepunkt von f.
6.5
Funktionen von mehreren Veränderlichen
Definition 6-1
Es sei n eine natürliche Zahl. Ist D ⊆
, dann heißt eine Vorschrift f : D → W , die jedem
n-dimensionalen Vektor x ∈ D genau ein Element y ∈ W mit W ⊆
on mit n Veränderlichen (Variablen).
zuordnet eine Funkti-
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
59
Definition 6-2
Es sei D ⊆
, und f : D → W eine Funktion mit zwei Veränderlichen, y = f ( x1 , x 2 ) . Hö-
henlinien oder Niveaulinien sind die geometrischen Orte aller Punkte (x1,x2), für die y = y
konstant ist. Die Gleichung der Höhenlinie ist implizit gegeben durch
f (x 1 , x 2 ) − y = 0 .
Definition 6-3
f(x) ist homogen vom Grade r, wenn gilt: f (λ x ) = λr f (x ),λ > 0 .
Beispiel 6-1
f (x ) = f (x 1 , x 2 ) = x 12 + x 22 , → f (λ x ) = f (λx 1 , λx 2 ) = (λx 1 ) + (λx 2 ) = λ2 f (x ) ,
2
2
d.h. f(x) ist homogen vom Grade 2
6.6
Partielle Ableitungen
Definition 6-1
Es sei D ⊆
und f : D → W und x 0 ∈ D . Für ein i, 1 ≤ i ≤ n heißt der Grenzwert (falls er
existiert)
lim0
(
)
(
f x10 ,… , x i0−1 , x i ,… x n0 − f x10 ,… , x i0−1 , x i0 ,… x n0
xi − xi
xi − x
)
0
i
die i-te partielle Ableitung der Funktion im Punkte x 0 . Für diese Ableitung schreiben wir
∂f
oder f xi , i = 1,2 ,… , n . f heißt (partiell) differenzierbar, wenn f xi für alle x 0 ∈ D und
∂x i
alle i = 1,2 ,… , n existiert.
Definition 6-2
Eine (partiell) differenzierbare Funktion mit n Veränderlichen besitzt n partielle Ableitungen
(1. Ordnung). Jede dieser n partiellen Ableitungen ist wieder eine Funktion von n Veränderli-
60
chen. Sind diese Funktionen wieder differenzierbar, dann können wieder partielle Ableitungen
(2. Ordnung, insgesamt n2) gebildet werden. Analog können partielle Ableitungen 3., 4. und
höherer Ordnung gebildet werden.
Satz 6-1
Es sei D ⊆
und f : D → W eine Funktion mit z = f ( x , y ) . f sei zweimal partiell diffe-
renzierbar. Sind die Ableitungen fxy und fyx stetig, so gilt
f xy ( x , y ) = f yx ( x , y ) für alle ( x , y ) ∈ D
Definition 6-3
Es sei D ⊆
und f : D → W mit y = f ( x ) . Das vollständige (totale) Differential von f
ist gegeben durch
dy = df ( x ) = f x1 dx1 + f x2 dx 2 +…+ f xn dx n
6.7
Extremwerte bei Funktionen von mehreren Veränderlichen
Satz 6-1
Es sei D ⊆
0
0
, x ein innerer Punkt von D und f : D → W sei partiell differenzierbar in
0
x . Wenn f in x einen Extremwert besitzt, dann gilt
( )
( )
( )
f x1 x 0 = f x2 x 0 =… = f xn x 0 = 0
(Notwendige Bedingung für ein relatives Extremum)
Definition 6-1
Es sei D ⊆
und f : D → W eine partiell differenzierbare Funktion. Die Lösungen des
Gleichungssystems
f x1 ( x ) = 0 ,
f x2 ( x ) = 0 ,… ,
f xn ( x ) = 0
heißen stationäre Punkte.
Satz 6-2
(Hinreichende Bedingung für einen relativen Extremwert im Fall n = 2)
Es sei D ⊆
und f : D → W mit z = f ( x , y ) eine Funktion mit stetigen partiellen Ablei-
tungen 2. Ordnung und ( x0 , y0 ) sei ein innerer Punkt aus D. Gilt
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
61
a) f x (x 0 , y 0 ) = 0 und f y (x 0 , y 0 ) = 0 und
b) ∆(x 0 , y 0 ) :=
f xx (x 0 , y 0 ) f xy (x 0 , y 0 )
= f xx (x 0 , y 0 )f yy (x 0 , y 0 ) − f xy2 (x 0 , y 0 ) > 0 ,
f yx (x 0 , y 0 ) f yy (x 0 , y 0 )
dann hat f an der Stelle ( x0 , y0 ) ein relatives Extremum.
Diese ist ein Maximum, falls f xx ( x0 , y0 ) < 0 ist und ein Minimum, falls f xx ( x0 , y0 ) > 0 ist.
Gilt dagegen a) und ∆( x0 , y0 ) < 0 , dann ist ( x0 , y0 ) kein Extremum, sondern es liegt ein Sattelpunkt vor.
Satz 6-3
(Hinreichende Bedingung für einen relativen Extremwert im Fall n > 2)
, f : D → W mit y = f ( x1 , x 2 ,… , x n ) eine Funktion mit stetigen partiellen
Es sei D ⊆
0
Ableitungen 2. Ordnung und x sei ein innerer Punkt aus D. Es gelte
( )
f x1 x 0 = 0 ,
a)
( )
f x2 x 0 = 0 ,… ,
( )
f xn x 0 = 0
Gilt
( )=
∆i x
b)
0
( )
(x )
( )
(x )
( )
(x ) > 0
f x1 x1 x
0
f x1 x2 x
0
…
f x1 xi x
0
f x2 x1
0
f x2 x2
0
…
f x2 xi
0
( )
f xi x1 x
0
( )
f xi x2 x
0
…
( )
f xi xi x
0
für alle i = 1,2 ,… , n , dann hat f an der Stelle x 0 ein Minimum.
( )
0
0
c) Gilt ( −1) ∆ i x > 0 für alle i = 1,2 ,… , n , dann hat f an der Stelle x ein Maximum.
i
( )
( )
0
0
0
d) Ist f xi xi x < 0 und f x j x j x > 0 , 1 ≤ i , j ≤ n , dann hat f an der Stelle x keinen Extrem-
wert.
( )
∆ n x 0 heißt Determinante der Hesse-Matrix von f im Punkt x 0 .
62
6.8
Extremwerte bei Nebenbedingungen
Satz 6-1 (Lagrangesche Multiplikatorregel für n = 2)
Es sei D ⊆
und f : D → W eine partiell differenzierbare Funktion mit y = f ( x1 , x 2 ) und
die Nebenbedingung laute g( x1 , x 2 ) = 0 .
Die notwendigen Bedingungen für relative Extremwerte von f unter der Nebenbedingung g
ergeben sich als stationäre Punkte der Lagrangefunktion
L( λ , x1 , x 2 ) = f ( x1 , x 2 ) + λg( x1 , x 2 )
λ heißt Lagrangemultiplikator. Es muss also folgendes Gleichungssystem gelöst werden
Lλ :
L x1 :
L x2 :
g (x 1 , x 2 ) = 0
f x 1 (x 1 , x 2 ) + λ g x 1 (x 1 , x 2 ) = 0
f x 2 (x 1 , x 2 ) + λ g x 2 (x 1 , x 2 ) = 0
Hinreichende Bedingungen:
Ist die Determinante der Hesse-Matrix von L am stationären Punkt positiv, so liegt ein Maximum vor, ist sie negativ, dann liegt ein Minimum vor.
L λλ
L λx 1
L λx 2
H = L x 1λ
L x 2λ
L x1 x 1
L x 2 x1
L x1 x 2
L x 2x 2
Satz 6-2 (Lagrangesche Multiplikatorregel für n > 2)
Es sei D ⊆
und f : D → W eine partiell differenzierbare Funktion mit y = f ( x ) und die
m(< n) Nebenbedingungen lauten g1 ( x ) = 0 , g2 ( x ) = 0 ,… , g m ( x ) = 0 . Die notwendigen Bedingungen für relative Extremwerte von f unter den m Nebenbedingungen ergeben sich als
stationäre Punkte der Lagrangefunktion
m
L( λ , x ) = f ( x ) + ∑ λ i g i ( x )
i =1
Zur Bestimmung der hinreichenden Bedingungen sind die Unterdeterminanten entlang der
Hauptdiagonalen -beginnend mit der Ordnung 2m+1 - der Hesse Matrix von L.
 L λ1λ1

 Lλ λ
H= 2 1

Lx λ
 n1
L λ1λ 2
L λ 2λ 2
L xnλ2
an den stationären Punkten zu untersuchen.
… L λ1x1
… L λ 2 x1
… L x n x1
… L λ1x n
… L λ2x n
… L xnxn







Prof. Dr. F.U. Mathiak, HS Neubrandenburg
63
Weisen die Unterdeterminanten alternierende Vorzeichen beginnend mit ( −1)
m+1
auf, so liegt
ein Maximum vor.
Weisen die Unterdeterminanten alle ein einheitliches Vorzeichen gegeben durch ( −1) auf, so
m
liegt ein Minimum vor.
6.9
Integralrechnung
Definition 6-1
Es seien in einem Intervall f ( x ) und F ( x ) gegeben. Es sei F ( x ) dort differenzierbar und es
sei dort stets
F ′( x ) = f ( x ) .
Dann heißt F ( x ) eine Stammfunktion oder ein unbestimmtes Integral von f ( x ) und wird
mit
∫ f ( x ) dx
bezeichnet.
Satz 6-1
Ist in einem Intervall F ( x ) Stammfunktion (unbestimmtes Integral) von f ( x ) , so hat jede
andere Stammfunktion von f ( x ) die Form F ( x ) + C mit C ∈
Satz 6-2
n
∫∑k
i =1
i
n
n
i =1
i =1
f i (x)dx = ∑ k i ∫ f i (x)dx = ∑ k i Fi (x) + C
Satz 6-3
a)
b)
∫ [f (x )] f ′(x )dx = α + 1 [f (x )]
α
1
α +1
+ C, α ≠ −1
f ′(x )
∫ f (x ) dx = ln f (x ) + C, f (x ) ≠ 0
.
64
Tabelle von Stammfunktionen
f ( x)
F( x)
f ( x)
F( x)
xα
1
x α +1 + C (α ≠ −1)
α +1
1
x
ex
ex + C
ln x
x ( ln x − 1) + C
sin x
− cos x + C
tan x
− ln cos x + C
cos x
sin x + C
cot x
ln sin x + C
ln x + C , x ≠ 0
(
)
(
)
arcsin x
x arcsin x + 1 − x 2 + C
arctan x
1
x arctan x − ln 1 + x 2 + C
2
arccos x
x arccos x − 1 − x 2 + C
arc cot x
1
x arc cot x + ln 1 + x 2 + C
2
sinh x
cosh x + C
tanh x
ln cosh x + C
cosh x
sinh x + C
coth x
ln sinh x + C
(
)
(
)
ar sinh x
xar sinh x − x 2 + 1 + C
ar tanh x
xar tanh x +
1
ln 1 − x 2 + C
2
ar cosh x
xar cosh x − x 2 − 1 + C
ar coth x
xar coth x +
1
ln x 2 − 1 + C
2
Satz 6-4
(Partielle Integration oder Produktintegration)
∫ f ( x )g ′( x ) dx = f ( x ) g( x ) − ∫ f ′( x )g( x ) dx
Satz 6-5
(Hauptsatz der Differential- u. Integralrechnung
Ist f ( x ) in [a , b] stetig und F ( x ) eine beliebige Stammfunktion von f ( x ) , so gilt
b
∫ f (x )dx = F(x )
a
Satz 6-6
a)
b
a
a
b
∫ f (x )dx = −∫ f (x )dx
a
b)
∫ f (x )dx = 0
a
b
a
= F(b ) − F(a )
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
c)
d)
b
c
b
a
a
c
65
∫ f (x )dx = ∫ f (x )dx + ∫ f (x )dx ,
a<c<b
b
b
b
a
a
a
∫ [k 1 f 1 (x ) + k 2 f 2 (x )]dx = k 1 ∫ f 1 (x )dx + k 2 ∫ f 2 (x )dx
Definition 6-2
Ist f ( x ) über jedem endlichen Intervall integrierbar, dann sind die uneigentlichen Integrale
von f ( x ) bei Existenz folgender Grenzwerte definiert als:
b
a)
b
∫ f (x )dx = lim ∫ f (x )dx
−∞
u →−∞
∞
b)
u
∫ f (x )dx = lim ∫ f (x )dx
a
u →∞
a
∞
c)
u
c
t
∫ f (x )dx = lim ∫ f (x )dx + lim ∫ f (x )dx für beliebiges c.
−∞
u →−∞
u
t →∞
c
66
7 Komplexe Zahlen
Definition 7-1
Komplexe Zahlen1 sind Ausdrücke der Form
z = x + iy
(x, y ∈ Ñ)
Das Symbol i bedeutet die imaginäre Einheit: i 2 = −1
( i ∉ Ñ). Es sind x der Realteil und
y der Imaginärteil der komplexen Zahl z
x = Re( z );
y = Im( z ) ;
z = Re( z ) + iIm( z )
Ist speziell y = 0, dann wird mit z = x + i ⋅ 0 die reelle Zahl x identifiziert; ist x = 0 und y ≠ 0 ,
dann ist z = 0 + iy = iy eine rein imaginäre Zahl.
Definition 7-2
Zwei komplexe Zahlen z 1 = x 1 + iy1 und z 2 = x 2 + iy 2 sind nur dann einander gleich
x 1 + i y1 = x 2 + i y 2
wenn x 1 = x 2 und y1 = y 2 gilt, also Real- und Imaginärteil je für sich gleich sind.
Definition 7-3
Die zu z = x + iy konjugiert komplexe Zahl z wird definiert durch:
z = x − iy
Damit sind:
a) Re(z ) = Re(z ) ;
b) Im(z ) = − Im(z )
c) z = z
⇔
z∈ Ñ
d) z = z
e) z 1 + z 2 = z1 + z 2
1
Geronimo Cardano, latinisiert Hieronymus Cardanus, italien. Mathematiker, Arzt u. Philosoph, 1501-1576
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
67
Definition 7-4
Der Betrag von z wird definiert durch: z = x 2 + y 2 = z z
Definition 7-5
Die Summe z 1 + z 2 der beiden komplexen Zahlen z 1 = x 1 + iy1 und z 2 = x 2 + iy 2 ist die
z = z 1 + z 2 = ( x 1 + x 2 ) + i( y 1 + y 2 )
komplexe Zahl:
Beispiel 7-1
z1 = 3 + 2i;
z 2 = 1 − 4i
→ z 1 + z 2 = 4 − 2i;
z 1 − z 2 = 2 + 6i
Definition 7-6
Das Produkt z 1 z 2 zweier komplexer Zahlen z 1 = x 1 + iy1 und z 2 = x 2 + iy 2 ist die komplexe
Zahl: z = z 1 z 2 = ( x 1 x 2 − y1 y 2 ) + i( x 1 y 2 + y1 x 2 )
Damit sind:
a) z z = x 2 + y 2 ≥ 0
b) z1 z 2 = z1 z 2
Beispiel 7-2
z 1 = 3 + 2i ; z 2 = 1 − 4i ;
z 1z 2 = (3 + 2i)(1 − 4i) = 3 − 12i + 2i − 8i 2 = 11 − i 10
z 1 z1 = 3 2 + 2 2 = 13
Definition 7-7 (Division komplexer Zahlen)
Unter der Voraussetzung z 2 ≠ 0 suchen wir diejenige Zahl z, für die bei vorgelegter Zahl z1
gilt: z 2 z = z1 . Erweiterung mit z 2 liefert z 2 z z 2 = z 1 z 2
z=
z 1 z 1 z 2 x 1 x 2 + y1 y 2
y1 x 2 − x 1 y 2
=
=
+
i
z 2 z2 z2
x 22 + y 22
x 22 + y 22
68
Beispiel 7-3
z 1 = 3 + 2i ; z 2 = 1 − 4i
z1 3 + 2i (3 + 2i )(1 + 4i ) 3 + 12i + 2i + 8i 2 − 5 + 14i
5 14
=
=
=
=
=− + i
z 2 1 − 4i (1 − 4i )(1 + 4i )
1 + 16
17
17 17
Definition 7-8
Der komplexen Zahl z = x + iy wird derjenige Punkt der Gaußschen Zahlenebene zugeordnet (Abb. 7-1), der in einem kartesischen Koordinatensystem die Abszisse x = Re(z) und die
Ordinate y = Im(z) besitzt.
Abb. 7-1 Gaußsche Zahlenebene
Die Menge der reellen Zahlen entspricht also den komplexen Zahlen z mit Im(z) = 0, weshalb
die Abszissenachse auch als reelle Achse bezeichnet wird. Den rein imaginären Zahlen z, also
allen Zahlen z mit Re(z) = 0, entspricht die Ordinatenachse, die deshalb auch als imaginäre
Achse bezeichnet wird.
Abb. 7-2 Addition und Subtraktion zweier Komplexer Zahlen
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
69
Hinweis: Oftmals ist es zweckmäßig, in der komplexen Ebene statt des beschriebenen Punktes, den Vektor-Pfeil zu betrachten, der vom Nullpunkt zum betrachteten Punkt hinweist
(Ortsvektor). Bei dieser Betrachtungsweise addieren sich zwei komplexe Zahlen wie die Kräfte in einem Kräfteparallelogramm. Die Differenz zweier komplexer Zahlen hat dann die Länge und Richtung der zweiten Diagonalen im Paralleleogramm (Abb. 7-2).
Der Zahl i entspricht der Punkt (0,1) der imaginären Achse und die Zahl 1 dem Punkt (1,0)
der reellen Achse. In der Geometrie der Ebene ist es üblich, neben den kartesischen Koordinaten, auch Polarkoordinaten zu benutzen. Ein Punkt in der Ebene wird dann beschrieben durch
seinen Abstand r = OP vom Koordinatenursprung 0 und dem Winkel ϕ , den der Fahrstrahl
von 0 nach P mit der positiven x-Achse einschließt (Abb. 7-3).
Abb. 7-3 Polarkoordinaten r, ϕ
Der Zusammenhang zwischen den kartesischen Koordinaten und den Polarkoordinaten ist
gegeben durch
x = r cos ϕ
y = r sin ϕ
Unter Beachtung der Euler-Identitäten e iϕ = cos ϕ + i sin ϕ; e −iϕ = cos ϕ − i sin ϕ lassen sich
die komplexen Zahlen auch in Polarkoordinaten darstellen.
Definition 7-9
z = x + iy = r (cos ϕ + i sin ϕ) = re iϕ
mit r = x 2 + y 2 = z
Definition 7-10
Der zur komplexen Zahl z ≠ 0 gehörige Winkel ϕ (Abb. 7-3) heißt Argument der komplexen
Zahl z und wird arg z = ϕ + 2πk
(k = 0,1, 2,.. ) geschrieben. Das Argument von z ist nicht
eindeutig bestimmt, sondern nur bis auf ganzzahlige Vielfache von 2π. Es ist also
z = z e i arg z
70
Hinweis: Mit den obigen Definitionen ist eine geometrische Interpretation der Multiplikation
und der Division komplexer Zahlen möglich. Es gilt nämlich für die beiden komplexen Zahlen z1 und z2:
z 1 = z 1 e i arg z1 , z 2 = z 2 e i arg z 2
dann gilt für das Produkt z 1 ⋅ z 2 einerseits
z1 ⋅ z 2 = z1 ⋅ z 2 e iarg( z1⋅z 2 )
und andererseits
z1 ⋅ z 2 = z1 e i argz1 ⋅ z 2 e i argz 2 = z1 ⋅ z 2 e i(arg z1 + arg z 2 )
Daraus folgt
Definition 7-11
arg(z1 ⋅ z 2 ) = arg z 1 + arg z 2 + 2kπ
Abb. 7-4 Multiplikation komplexer Zahlen
Abb. 7-5 Division komplexer Zahlen
Aus den obigen Betrachtungen ergeben sich nun einfache geometrische Darstellungen der
Multiplikation und der Division komplexer Zahlen.
Multiplikation:
Wir drehen den Vektor z2 im positiven Sinne um den Winkel ϕ und strecken ihn im
Verhältnis 1:ρ = 1: z1 Der neue Vektor stellt dann das Produkt z 1 ⋅ z 2 dar.
Die Multiplikation komplexer Zahlen entspricht einer Drehstreckung (Abb. 7-4).
Division: Für den Quotienten z1/z2 erhalten wir
Prof. Dr. F.U. Mathiak, HS Neubrandenburg
71
z
z1
= 1 e i (arg z1 −arg z 2 )
z2
z2
Dieses Ergebnis deuten wir wie folgt:
Drehen wir den Vektor z2 im negativen Sinne um den Winkel ϕ und strecken ihn im
Verhältnis ρ:1, so erhalten wir den Vektor z = z1/z2 (Abb. 7-5)
Definition 7-12
Aus z = z e i argz erhalten wir für die n-te Potenz von z: z n = z ei⋅n⋅argz und es gilt:
n
arg(z n ) = n arg(z) + 2kπ
Bezeichnen wir die Lösungen von z n = w generell mit z = n w , dann folgt
arg(n w ) =
1
2 kπ
arg( w ) +
n
n
i
n
w = n w en
arg( w ) +
2 πik
n
(k = 0,1,… , n − 1)
Hinweis: Es genügt, wenn wir uns auf die Werte k = 0,1, … , n − 1 beschränken, da wir für die
anderen Werte k ∈ Z periodisch immer wieder dieselben komplexen Zahlen erhalten.
Beispiel 7-4
Insbesondere erhalten für w = 1 die n-ten Einheitswurzeln
n
1=e
2 kπi
n
= cos
2πk
2πk
+ i sin
n
n
(k = 0,1, … , n − 1)
Sie bilden geometrisch die Eckpunkte eines nEcks. Das n-Eck hat stets den auf der reellen
Achse gelegenen Punkt z 0 = 1 zur Ecke. Alle
Eckpunkte z 0 , z 1 ,…, z n −1 genügen der Gleichung
x n −1 = 0
die Kreisteilungsgleichung genannt wird,
weil die Lösungsmenge den Umfang des EinAbb. 7-6 Sechste Einheitswurzeln
heitskreises in n gleiche Teile teilt.