Kapitel 1 - Mikroökonomische Methodik

Kapitel 1 - Mikroökonomische Methodik
[ Exogene Variable : durch Einflüsse hervorbestimmt, die nicht im Modell diskutiert werden
Endogene Variable: durch Kräfte hervorbestimmt, die im Modell beschrieben werden ]
Grundprinzipien der VWL:
Optimierungsprinzip der Wirtschaftssubjekte:
 Mitteloptimierung: mit vorgegebenen Mitteln das bestmöglichste Ergebnis erzielen
 Zieloptimierung: ein vorgegebenes Ziel mit möglichst minimalen Aufwand erreichen
Gleichgewichtsprinzip hinsichtlich des Funktionierens des Marktes:
Die Preise passen sich solange an, bis Nachgefragte Menge gleich angebotener Menge
Nachfragekurve:
= eine Kurve, die die nachgefragte Menge zum Preis in Beziehung setzt
= wieviel die WS zu jedem Preis nachfragen
[ Vorbehaltspreis / Reservationspreis eines WS
= maximale Zahlungsbereitschaft
= der höchste Preis der beim Kauf eines Gutes gerade noch akzeptabel ist
= der Preis, bei dem das WS indifferent zwischen Kauf und Nichtkauf des Gutes ist ]
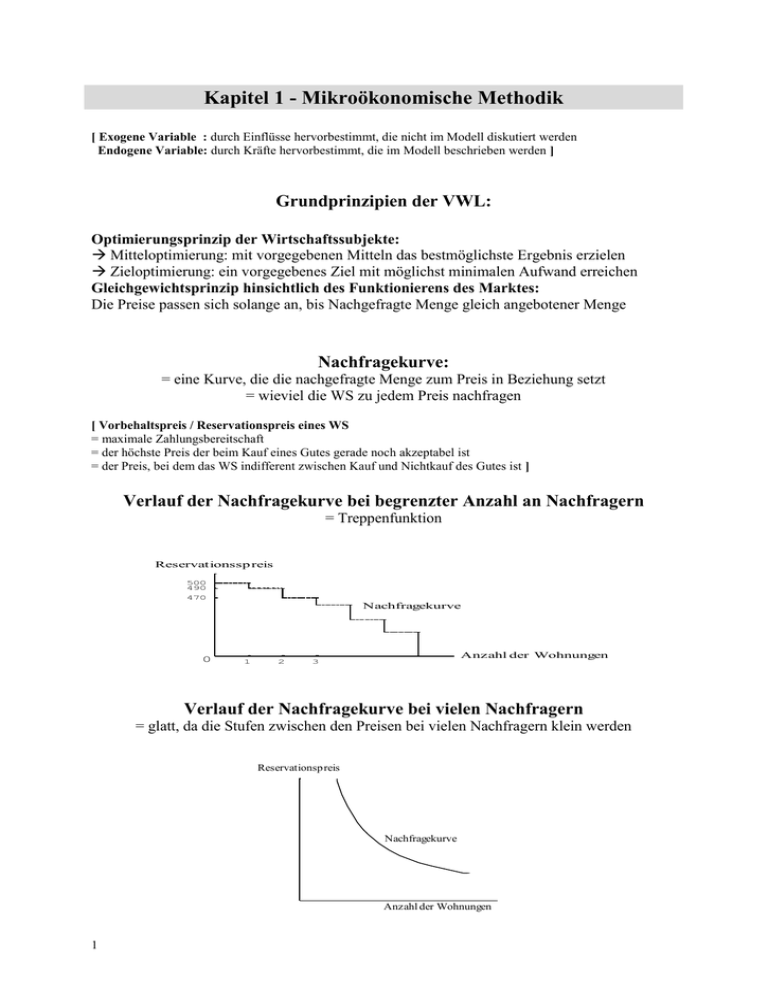
Verlauf der Nachfragekurve bei begrenzter Anzahl an Nachfragern
= Treppenfunktion
Reservationssp reis
500
490
470
Nachfragekurve
0
1
2
Anzahl der Wohnungen
3
Verlauf der Nachfragekurve bei vielen Nachfragern
= glatt, da die Stufen zwischen den Preisen bei vielen Nachfragern klein werden
Reservationspreis
Nachfragekurve
Anzahl der Wohnungen
1
Angebotskurve:
= wieviel die WS zu jedem Preis anbieten wollen
Kurzfristige Angebotskurve
= z.B: unabhängig vom Preis wird immer diesselbe Anzahl an Wohnungen vermietet, nämlich
alle zu diesem Zeitpunkt verfügbaren Wohnungen
[ Konstante Anzahl an Wohnungen = S ]
Reservationsp reis
Angebot
S
Anzahl der Wohnungen
Gleichgewichtsverhalten des Marktes:
Angebots- und Nachfragekurve werden in dieselbe Graphik gezeichnet; der Schnittpunkt
beider Kurven ist der Gleichgewichtspreis p*, bei dem Angebots- und Nachfragemenge gleich
groß sind.
Reservationsp reis
Angebot
p*
Nachfrage
S
2
Anzahl der Wohnungen
Komparative Statik
= die Analyse der Veränderung von Gleichgewichtspreis und -menge bei Veränderung der
zugrundeliegenden Bedingungen.
Angebot wird erhöht  Gleichgewichtspreis fällt
Angebot wird gesenkt  Gleichgewichtspreis steigt
Reservationspreis
altes
neues
Angebot Angebot
p* alt
p* neu
Nachfrage
S´
S
Anzahl der
Wohnungen
Mietwohnungen werden in Eigentumswohnungen umgewandelt:
Vermutung: Miete steigt aufgrund Verringerung des Angebots
Aber: einige Mieter erwerben eine Eigentumswohnung, d.h. die Nachfrage nach
Mietwohnungen verringert sich auch
Fazit: die Auswirkungen einer Änderung einer der exogenen Variablen ist sowohl das
Angebot als auch die Nachfrage zu berücksichtigen!
Der alte Gleichgewichtspreis ist gleich dem neuen, wenn sich Angebot und Nachfrage im
gleichen Ausmaß verschieben.
Reservationspreis
neues
altes
Angebot Angebot
p
Nalt
Nneu
S´
S
Anzahl der Wohnungen
Pareto-Effizienz
= zur Beurteilung verschiedener Arten der Ressourcenallokation
pareto-effiziente Allokation = wenn es keine andere Möglichkeit gibt, eine Person besser zu
stellen, ohne irgendeine andere zu benachteiligen.
pareto-ineffiziente Allokation = wenn irgendeine Möglichkeit gefunden werden kann,
zumindest eine Person besser zu stellen, ohne jemand anderen zu benachteiligen
3
Kapitel 2 – Theorie des Haushaltes
[ Konsumbündel X = eine vollständige, d.h. dass alle für die Konsumentscheidung
relevanten Waren und Dienstleistungen enthalten sein müssen
Vereinfachter Fall: es gibt nur zwei Güter: Gut 1 = x1 und Gut 2 = x2
Konsumbündel X = (x1,x2)
[im Falle von mehr als zwei betrachteten Gütern schreibt man: X=(x1,x2,...,xn)]
Warenkörbe/Güterbündel/Konsumpläne = graphische Darstellung aller Kombinationen
dieser beiden Güter
x2
X

x1
Güterraum = alle Kombinationen der beiden Güter
Konsummenge = der Teilraum der Gütermenge, der das Überleben des Konsumenten
sicherstellt = schraffierte Fläche]
4
Präferenzrelation
= Art der Bewertung unterschiedlicher Warenkörbe
Notation für Präferenzrelationen:
Betrachten wir einmal die beiden Güterbündel x = (x1 ,x2 ) und y = ( y1 , y2 ) im Vergleich zueinander:
Wenn der Konsument das Güterbündel x =(x1 ,x2 ) dem Güterbündel y =( y1 , y2 ) gegenüber ...
... strikt bevorzugt:
(
x1 , x2 )
 ( y1 , y2 ).
... als gleich gut bewertet / Der Konsument ist indifferent zwischen x und y:
( x1 ,x2 )  ( y1 , y2 ).
... schwach präferiert / als mindestens so gut bewertet:
( x1 ,x2 )  ( y1 , y2 ).
Diese Relationen hängen wie folgt zusammen:
( x1 ,x2 )  ( y1 , y2 ) und ( y1 , y2 )  ( x1 ,x2 )  ( x1 ,x2 )  ( y1 , y2 ).
Eigenschaften von Präferenzrelationen:
1. Vollständigkeit
Ein Konsument kann alle Güterbündel im paarweisen Vergleich bewerten.
Für alle x und y gilt: x  y oder y  x.
Hierbei enthalten: Reflexivität: x  x.
Die Reflexivität erscheint zunächst irrational – dies auch begründet; allerdings kann man bei Kindern häufig
noch beobachten, dass zwei Kleinkinder genau das Gleiche zum Spielen geschenkt bekommen, dem anderen
seines aber trotzdem neidet, weil dieses besser sei.
2. Transitivität
Für die drei Güterbündel x, y, z gilt: Wenn x  y und y  z dann gilt auch x  z.
Dies ist eine Annahme an das Rationalverhalten. Was würde man von jemanden halten, der Äpfel lieber mag
als Birnen, Birnen lieber als Orangen, aber Orangen lieber als Äpfel, also intransitive Präferenzen hätte? In
diesem Fall gibt es kein bestes Güterbündel.
3. Monotonie
Es wird angenommen, dass wir es nicht mit Schlechten zu tun haben. Ein Güterbündel, das von mindestens
einem Gut mehr enthält (und von keinem anderen weniger) wird präferiert:
(
x1 ,x2 )
 ( y1 , y2 ). Die Monotonie führt dazu, daß die Kurven eine negative Steigung haben.
x2
Bessere Güterbündel

x1 ,x2 
Schlechtere Güterbündel
x1
5
4. Konvexität
Diese Annahme besagt, daß Mischungen von Güterbündeln besser (d.h. zumindest so gut oder strikt bevorzugt )
sind als Extreme.
Betrachten wir zwei indifferente Güterbündel ( = auf derselben I-Kurve ):
x = (x1 ,x2 ) und y = ( y1, y2) mit (x1 ,x2 ) ( y1, y2).
1
1
1
1
€€
€€
€€
€€ €€
€€
€€
€€
Bildet man eine Mischung aus x und y, z.B.: ( 2 x1 + 2 y1, 2 x2 + 2 y2)
oder allgemein für konvex: (tx1 + (1-t) y1, tx2 + (1-t) y2 )  (x1 ,x2 )
mit t  [0,1]
(tx1 + (1-t) y1, tx2 + (1-t) y2 )  ( y1, y2);
(tx1 + (1-t) y1, tx2 + (1-t) y2 )  (x1 ,x2 )
und für streng konvex:
mit t  [0,1]
(tx1 + (1-t) y1, tx2 + (1-t) y2 )  ( y1, y2);
Konvexe Präferenzen: die Verbindungslinie zweier beliebiger Punkte liegt zur Gänze innerhalb der
Menge. Konvexe Präferenzen können Flachstellen aufweisen.
Streng konvexe Präferenzen: das Durchschnittsbündel wird den beiden extremen Bündeln streng
bevorzugt. Streng konvexe Präferenzen müssen runde Indifferenzkurven aufweisen .
y
x
æ
tx +
H
L
1- t y
y
x
streng konvex
y
HL
t x + 1- t y
æ
x
æ
æ
y
x
konvex ( rechts: perfekte Substitute ) aber nicht streng konvex

x
tx  1 
t y


y
nicht-konvex
( d.h. ich mag z.B. Eiscreme und Fisch – aber nicht miteinander! In diesem Fall sind die Extreme besser. )
6
Indifferenzkurven
= graphische Darstellung von Präferenzen
Eigenschaften von Indifferenzkurven:
Stetigkeit : Die Indifferenzkurve durch ein Konsumbündel besteht aus allen Güterbündeln,
zwischen denen der Konsument in bezug auf das gegebene Güterbündel indifferent ist: x~u

Essen kg Woche
wæ
zæ
besser als x
xæ
schlechter als x uæ
væ

yæ
Wohnen m2 Woche
Indifferenzkurven, die verschiedene Präferenzniveaus darstellen, können sich nicht schneiden, würden sie das, so
wären X, Y und Z indifferent zueinander und könnten daher nicht auf verschiedenen Indifferenzkurven liegen.
x2
x
æ
æ
z
y
x1
Den einzelnen Indifferenzkurven verschiedener Güterbündel können reelle Zahlen zugeordnet werden. Wie
genau diese Zahlen lauten, spielt keine Rolle, entscheidend ist nur, dass höhere Indifferenzkurven auch höhere
Zahlen erhalten.
x2
I4
I3
I2
I1
7
x1
Typen von Indifferenzkurven
bei zwei Gütern:
Perfekte Substitute:
Zwei Güter sind perfekte Substitute, wenn der Konsument bereit ist, ein Gut für das andere zu einem konstanten
Verhältnis zu tauschen. Einfachster Fall: 1:1
Hierbei ist es dem Konsumenten gleichgültig, ob er eine Mischung der beiden Güterbündel oder die
Extrempunkte erhält ( Konsument benötigt zehn Stifte, egal ob schwarz oder blau; er kann zehn schwarze oder
zehn blaue oder auch eine Mischung fünf zu fünf / drei zu sieben / ... wählen )
Diese Indifferenzkurven haben immer eine konstante Steigung und schneiden die Koordinatenachsen
blaue Stifte
rote Stifte
Perfekte Komplemente:
Perfekte Komplemente sind Güter, die immer in konstantem Verhältnis miteinander konsumiert werden – in
diesem Sinne ergänzen sich diese Güter. Mehr von einem Gut, ohne dass auch gleichzeitig mehr von dem
anderen konsumiert wird, ist für den Konsumenten nicht von Nutzen.
Die Indifferenzkurve ist L-förmig, mit der Ecke des L´s dort, wo die Anzahl bzw. das Verhältnis der beiden
Güter zueinander passend ist. ( z.B. eine Tasse Kaffe, zwei Stück Zucker; zwei Tassen Kaffee, vier Stück
Zucker; unpassend wären für diesen Konsumenten eine Tasse Kaffe und vier Stück Zucker )
Zucker
Kaffee
Schlechtes Gut
= eine Ware, die der Konsument nicht mag
der Konsument mag keine Sardellen, aber Wurst; gibt man diesem Konsumenten mehr Sardellen, um so mehr
Wurst muß man ihm als Entschädigung hinzugeben
Daher steigt die Indifferenzkurve nach rechts oben ( positive Steigung ), wobei die Richtung zunehmender
Präferenzen nach rechts unten zielt.
x2
x1
8
Neutrales Gut
= wenn der Konsument eines der Güter weder mag noch verabscheut
ihm ist in diesem Fall egal ob oder wieviel er von x2 besitzt, solange er das erwünschte x1 nicht missen muß –
daher sind diese Indifferenzkurven vertikale Gerade
x2
x1
Sättigung
= insgesamt bestes Bündel für den Konsument = Sättigungs – oder Blisspunkt
hier sind Mischungen aus zwei Güterbündeln grundsätzlich besser, denn verbindet man zwei beliebige
Güterbündel miteinander, so liegt die Verbindungslinie stets näher am Blisspoint als die Ausgangspunkte.
x2
æ
x1
Typen von Indifferenzkurven
bei drei Gütern:
hierbei handelt es sich nicht mehr um Kurven sondern um Flächen
9
Die Grenzrate der Substitution / GRS
x2
Dx2
x1
Dx 1
Hier wäre der Konsument bereit, für die Menge x1 , die Menge x2 aufzugeben, denn er bleibt ja auf der
gleichen Indifferenzkurve. Das Verhältnis oder die Rate, mit der der Konsument zu tauschen bereit ist, kann also
geschrieben werden als:
D x2
€€€€€€€€
€€€€
€€
€
D x1 .
Diese Rate ist aber offensichtlich abhängig davon, wie groß x1 gewählt wird. Es wäre schön, wenn man diese
Rate, mit der ein Konsument zu tauschen bereit ist, unabhängig von x1 angeben könnte. Dies erreicht man
dadurch, daß man x1 gegen 0 streben läßt. In diesem Fall ist diese Tauschrate, also die Rate, mit der ein
Konsument bereit ist, x1 gegen x2 zu substituieren, durch die Steigung der Indifferenzkurve gegeben.
x2
X
Dx2
x1
Dx1
Die MRS ist eine negative Zahl, da monotone Präferenzen eine negativ geneigte I-Kurve implizieren.
Offensichtlich ist die Steigung einer Indifferenzkurve aber auch davon abhängig, an welcher Stelle wir diese
Steigung betrachten.
x2
x
x´
x´´
x1
Offensichtlich gilt also:
Sind die Präferenzen streng konvex, dann nimmt die Grenzrate der Substitution mit x1
( siehe obige Graphik ).
Bei linearen Präferenzen ist die GRS konstant bei –1 (perfekte Substitution).
Bei neutralen Gütern ist die GRS überall unendlich.
Bei perfekten Komplementen ist die GRS entweder 0 oder unendlich
10
ab
Nutzenfunktionen
Es wurde bereits darauf hingewiesen, daß man Indifferenzkurven Zahlen zuordnen kann, so
daß präferierte Güterbündel höhere Zahlen erhalten, und indifferente Güterbündel die gleiche
Zahl. Dieses Konzept kann verallgemeinert werden zum Konzept der Nutzenfunktion. Eine
Nutzenfunktion ist eine numerische Darstellung einer Präferenzordnung.
Ein Güterbündel (x1 ,x2 ) wird gegenüber ( y1 , y2 ) strikt präferiert, genau dann, wenn der
Nutzen von (x1 ,x2 ) größer ist als der Nutzen von ( y1 , y2 ).
Symbolisch:
(x1 ,x2 )  ( y1 , y2 ) wenn und nur wenn u(x1 ,x2 ) > u( y1 , y2 ).
Wie wir gesehen haben, spielt nur die Reihenfolge der Zahlen (höhere Zahlen  präferierte
Güterbündel), nicht aber deren absolute Größe, eine Rolle. Daher kann man auch alle
Nutzenwerte mit...
... einer beliebigen Zahl addieren,
... einer positiven Zahl multiplizieren,
... einer ungeraden Zahl multiplitieren
... ,ohne die Reihenfolge zu ändern.
Es gibt also für eine gegebene Präferenzordnung keine eindeutige Nutzendarstellung.
Genauer: Jede positiv monotone Transformation einer Nutzenfunktion ist selbst wieder eine
Nutzenfunktion, die die gleichen Präferenzen darstellt. Dabei heißt "positiv montone
Transformation" eine Funktion f (u(·)), die die Reihenfolge der Zahlen unverändert läßt.
Eine monotone Transformation hat immer eine positive Änderungsrate, die Graphik hat also
immer eine positive Steigung.
11
Beispiele für Nutzenfunktionen
Im ersten Teil dieses Kapitels wurden einige Beispiele für Präferenzen samt den zugehörigen I-Kurven
beschrieben. Man kann diese Präferenzen auch durch Nutzenfunktionen darstellen. Für jeden unterschiedlichen
Wert der Konstanten u erhält man eine andere Indifferenzkurve.
Cobb-Douglas Funktion
Leontief Funktion
2
1.5
1.5
1
0.5
0
1
0.5
0
2
2
2
1.5
1.5
1
1
0.5
0
0
0.5
0.5
1
1.5
0
2
u ( x1 ,x2 ) = x1 x2
1
1.5
2
für perfekte Komplemente
u (x1 ,x2 ) = min ( ax1 ,bx2 )
Minimum, welches von beiden Gütern benötigt
wird (z.B. ein linker und rechter Schuh )
a und b = positive Zahlen, die das Verhältnis
angeben in welchem die Güter konsumiert werden
a und b = positive Zahlen, welche die
Präferenzen d. Konsumenten beschreiben
Lineare Funktion
CES Funktion
2
2
1.5
1.5
1
1
0.5
0.5
0
0
1
3
0.5
2.5
0
0
2
0
0.5
0.5
1
1
1.5
1.5
2
für perfekte Substitute
u ( x 1 , x 2 ) = a x 1 + bx 2
a und b = positive Zahlen = der „Wert“ der
Güter 1 und 2 für den Konsumenten
12
0
0.5
2
u (x1 ,x2 ) = [ ax1 + bx2
] für
1 und = 0
Die CES-Funktion enthält alle drei Funktionen:
für

1 = Lineare Funktion
für

- = Leontif-Funktion
für

0 = Cobb-Douglas-Funktion
Man kann nun auf der Oberfläche alle diejeingen Güterbündel markieren, die den gleichen Nutzen stiften. Man
erhält also sogenannte Isohöhenlinien. Graphisch können diese wie folge dargestellt werden:
Isohöhenlinien
x2 1.5
1
2
0.5
0
2
1.5
y
1
0.5
0
0
0.5
1
x1
1.5
2
Die Grenzrate der Substitution kann auch mathematisch hergeleitet werden. der Nutzen auf
Indifferenzkurven ist konstant – die Nutzenänderung gleich null:
HL HL
H

HL
L

Wenn wir jetzt das totale Differential dieser Nutzenfunktion betrachten,ergibt sich:
¶ u x1 , x2
¶ u x1 , x2
€€€€€€€€€€€€€€€€
€€€€€€€€€€€€€€€€
€€€€
€€
€
€€€€€€€€€€€€€€€€
€€€€€€€€€€€€€€€€
€€€€
€€
€
¶ x1
¶ x2
du =
dx1 +
dx 2 = 0

¶u x1 ,x2 ¶x 1
d x2
€€€€€€€€
€€
€€€€€€€€
€€
€€ €€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€€
d x 1 = - ¶u x1 ,x2 ¶x 2
Die Grenzrate der Substitution ist also gleich dem umgekehrten Verhältnis des
Grenznutzens.
13
Kapitel 3 – Nutzenmaximierung und Nachfrage eines Haushaltes
Die Budgetmenge
Der Konsument ist in seinen Möglichkeiten im allgemeinen durch sein Einkommen bzw. Vermögen beschränkt.
Er kann sich eben nicht jedes Güterbündel leisten. Um nun zu verstehen, was "leisten können" bedeutet, müssen
die Preise der Güter eingeführt werden.
Die Preise der Güter werden durch reelle Zahlen
p1 , p2 ,..., pn
Damit können wir nun den Wert eines Güterbündels beschreiben:
ausgedrückt.
p1 x1 + p2 x2
n
oder allgemein:
p1 x1 + p2 x2 + ... + pn xn =
p1x2mitp1x1 p = ( p1 , p2 ,..., pn ) und
p2
pn
S
pi xi = px
x = ( x1 , x2 ,..., xn ).
i= 1
Das Budget eines Konsumenten ist gegeben durch m, dann ist die Menge der Güterbündel, die sich der
Konsument leisten kann, d.h. deren Wert das Einkommen nicht übersteigt, gegeben durch
p1 x1 + p2 x2
m
p1 x1
oder allgemein durch
x2
+ ... +
pn xn
p
1m
p1 x1
Die Menge dieser Güterbündel, die sich ein Haushalt leisten kann, ist beschrieben durch seine Budgetmenge /
Budget:
B = {x  X | p1 x1 + .... + pn xn  m }
Im Falle von zwei Gütern kann man die Budgetmenge graphisch wie folgt darstellen:
x2
m
€€€€
€€
€€
€
æ
p2
Budgetmenge
m
€€€€
€€
€€
€
p1
æ
x1
Den Rand der Budgetmenge, die sogenannte Budgetgerade ist jene Menge der Güterbündel, die genau m
kosten, also jene Güterbündel, die m zur Gänze ausschöpfen:
p1 x1 + p2 x2 = m
Die
p1 Budgetgerade kann man wie folgt ermitteln:
x2 aus, dann kann
m
m
€€€€€€€€
€€
€€€€€€€€
€€
p
p
x
1
2
1
man sich hiervon
Einheiten leisten bzw. im Falle von
,
Einheiten.
1) Ermittlung der Randpunkte auf den Achsen: Gibt man m gesamt für
2) Verbinden dieser beiden Punkte durch eine Gerade.
Die Steigung der Budgetgeraden mißt das Verhältnis, zu dem der Konsument bereit ist, Gut 1 für Gut 2 zu
substituieren. Die Steigung der Budgetgeraden ist gleich dem (negativen) Preisverhältnis.
Die Steigung der Budgetgeraden kann man wie folgt feststellen:
p1 x1 + p2 x2 = m muß erfüllt sein
p1 ( x1 + x1 ) + p2 ( x2 + x2 )= m muß erfüllt sein
(1)
(2)
(1) = (2) liefert
p1 x1 + p2 x2
p1
dx2
€€€€€€€€
€€€€
€ €€€€€€€€
€€
p2
dx1
[ = Opportunitätskosten von Gut 1 ]
0=
14
Änderungen der Budgetgeraden
1) Einkommensänderug:
a) Einkommenserhöhung ( bei konstanten Preisen ):
 Parallelverschiebung der Budgetgeraden nach außen, keine Änderung der Steigung, da
das Preisverhältnis das gleiche geblieben ist – man kann sich nun nur mehr leisten
b) Einkommenssenkung ( bei konstanten Preisen ):
 Parallelverschiebung der Budgetgeraden nach innen, keine Änderung der Steigung, da
das Preisverhältnis das gleiche geblieben ist – man kann sich nun nur weniger leisten
x




2
m


m
m´
p1


x1







2) Preisänderung:
a) Preiserhöhung für Gut 1 ( bei konstantem p2 und m ):
b)
Wenn man sein gesamtes Einkommen für das Gut 2 ausgibt, dann spielt die Preisänderung für das Gut 1
keine Rolle. Der Haushalt kann sich weiterhin dieselbe Menge von Gut 2 leisten wie vor der Preiserhöhung,
der Ordinatenabschnitt bleibt unverändert Allerdings ändert sich die Menge, die der Haushalt von Gut 1
kaufen kann – der Abszissenabschnitt verschiebt sich nach innen.
Analog gilt eine ähnliche Aussage auch für eine Preisänderung für Gut 2.
x2
m
€€€€
€€
€€
€
p2
p´1 > p1
m
€€€€
€€
€€
€
p´1
x1
m
€€€€
€€
€€
€
p1
c ) Werden beide Güterpreise um den gleichen Betrag t erhöht oder gesenkt, dann bleibt das
Preisverhältnis gleich, aber die Budgetgerade verschiebt sich nach innen bzw. außen:
p1
p1
15
t
p1 x1 +
t

p1 x1 + p2 x2
p2 x2
m
= m/t
=
Mengenrabatt / Rationierung / Transportkosten
-
Angenommen, ab einer bestimmten Menge von Gut 1 ( x1 ) kann man zusätzliche Einheiten
des Gutes zu einem geringeren Preis kaufen (Mengenrabatt). Ab diesem Punkt ändert sich
das Preisverhältnis und damit die Steigung der Budgetgeraden.
x2
10
8
6
4
æ
2
2
È

x
1
4
6
8
x1
Budgetgerade bei Mengenrabatt
Ähnlich "geknickte" Budgetgeraden entstehen u.a. bei Rationierungen (d.h., wenn man nur
eine maximale Menge eines Gutes konsumieren darf).
x2
x1
Budgetgerade bei Rationierung von Gut
x1
Bei Gut 2 kommen neben den normalen Kosten zusätzlich noch Transportkosten hinzu,
diese ergeben im Schaubild isolierte Punkte:
16
Optimale Entscheidung
= das beste Bündel, das sich der Konsument leisten kann
Wir haben nun zum einen die Präferenzen (bzw. Nutzenfunktionen) eines Haushaltes und zum anderen die
Menge der Güter charakterisiert, die der Haushalt sich leisten kann. Mit diesen beiden Konzepten kann nun die
optimale Entscheidung eines Haushaltes analysiert werden.
Tragen wir einmal die Budgetmenge zusammen mit einigen Indifferenzkurven in ein Diagramm ein:
x2
x *2
x*
x*1
x1
Der Haushalt möchte sein Nutzenmaximum, muß aber dabei berücksichtigen, daß er nur Güterbündel innerhalb
der Budgetmenge wählen darf - bei monotonen Präferenzen auf der Budgetgeraden.
Aber nicht jedes Güterbündel auf dem Rand der Budgetmenge ist optimal. Das beste Güterbündel ist dasjenige,
das von der höchsten Indifferenzkurve gerade noch erreicht wird. Dies ist der Punkt der Budgetmenge, der von
einer Indifferenzkurve tangiert wird und mit optimaler Entscheidung (x1*,x2*) bezeichnet wird.
Hier ist die Steigung der Indifferenzkurve gleich der Steigung der Budgetgeraden.
Dies gilt aber nur für streng konvexe Präferenzen immer; die Tangentialbedingung muss nicht in allen Fällen
gelten ( Ausnahmen siehe Seiten ff ).
Man könnte nun (für alle Preis-Einkommenskombinationen) die nutzenmaximierenden
Mengen der Güter notieren. Man würde also erhalten:
x1 ( p1 , p2 ,m) und x2 ( p1 , p2 ,m) .
Diese Funktionen bezeichnet man als Nachfragefunktionen, bisweilen auch Marshallsche
Nachfragefunktionen. Also ist die Nachfragefunktion jene Funktion, welche die optimale
Entscheidung – die nachgefragten Mengen – zu den verschiedenen Werten von Preisen und
Einkommen in Beziehung setzt.
Formal erhält man diese Nachfragefunktionen, indem man die Bedingungen erster Ordnung
heranzieht und nach x1 und x2 als Funktion der Parameter p1 , p2 und m auflöst. Dies
werden wir anhand eines Beispiels durchführen.
Vorher betrachten wir aber, ebenfalls als Beispiele, die Situation vollkommener Substitute
und vollkommener Komplemente. In diesen Fällen kann man die Nachfragefunktion ohne
Rechnen, d.h. nur durch einige Überlegungen herleiten.
17
Ausnahmen:
Konvexe, aber nicht streng konvexe Präferenzen:
a ) Vollkommene Substitute:
1) Randoptimum: Hier liegt der optimale Punkt dort, wo der Konsum eines Gutes gleich Null ist.
x2
x2
10æ
10
8
8
6
6
I
4
4
2
B
B
I
2
2
4
æ
6
8
10
x1
2
4
æ
6
8
10
x1
Durch Überlegen hergeleitet:
Im Fall p1 < p2 ist die Steigung der Budgetgeraden flacher als die Steigung der Indifferenzkurve. Der
Konsument wird sein gesamtes Einkommen für Gut 1 ausgeben.
m
€€€€€€€€
€€
€
Im Fall p1 = p2 wird er indifferent sein zwischen Mengen von Gut 1 zwischen 0 und p1 (unterstellt, er
gibt jeweils den Rest seines Budgets für Gut 2 aus). Hier ist jede Mengenkombination der beiden Güter optimal,
welche die Budgetbeschränkung erfüllt.
Im Fall p1 > p2 wird der Konsument sein gesamtes Einkommen für Gut 2 ausgeben.
m
p 1
, falls







p2;
p1
x1 ( p1 , p2 ,m) =
{
Formal hergeleitet:
H
L
HL
HL
HL


m
p 1
0, 





, falls
p2;
p1
p 
0, falls
p .
0, falls p1 > p2.
Hier lautet die Bedingung für eine optimale Lösung:
¶u x , x
1 €€€€
2€€
€€€€€€€€€€€€€€€€
€€€€€€€€
€€
¶x1
1
€€€€€€€€€€€€€€€€
€€€€€€€€€€€€€€€€
€€
€
€€€€€€€€
€€
¶u x€€€€€€€€
1, x€€€€
2€€
€€€€€€€€€€€€€€€€
€€  2
¶x2
p
p
Eine solche Lösung erhält man mit Hilfe der Kuhn-Tucker-Bedingungen.
Diese besagen:
¶u x1 , x2
€€€€€€€€€€€€€€€€
€€€€€€€€
€€€€€€€€
€€
€ -  p1
¶x
1
und
¶u x1 , x2
€€€€€€€€€€€€€€€€
€€€€€€€€
€€€€€€€€
€€
€
-  p1
¶x
1
18
0
0
wenn x1 > 0.
2 ) Kontinuum an Lösungen: Steigung der Indifferenzkurve gleich der Steigung der Budgetgeraden
Hier gibt es überabzählbar unendlich viele Lösungen  keine optimale Entscheidung möglich
x2
10
8
6
I, B
4
2
2
4
6
8
10
x1
b ) Perfekte Komplemente:
Hier hat die Indifferenzkurve bei der Optimalen Entscheidung einen Knick und es gibt keine Tangente an diesen
Punkt.
x2
æ
x
x1
Hier sieht man, daß der Konsument immer Güterbündel auf der Diagonalen wählen wird, egal
wie die Preise sind, d.h. er wird immer die gleiche Menge beider Güter kaufen. Diese Menge
x
ist mit = x1 = x2 bezeichnet.
Es gilt also:
p1 x1 + p2 x2 = m
m
€€€€€€€€€€€€€€€€
€€€€€€€€
€€
€€
x x1 x2
p
+
p
1
2
=
=
=
Da beide Güter immer zusammen konsumiert werden, ist es gleichsam so, als würde der
Konsument nur ein Gut (x) zum Preis von p1 + p2 kaufen.
Nichtkonvexe Präferenzen:
x2
xæ
æ
x¢
x1
Hier können multiple Optima auftreten.
19
Konkave Präferenzen
Die optimale Entscheidung ist der Randpunkt Z und nicht der innere Berührungspunkt X, da Z auf einer höheren
Indifferenzkurve liegt.
Bild 5.8 Buch S. 76  Papa scannen
Betrachten wir zum Schluß den Fall, in dem die Präferenz eines Konsumenten durch die
Cobb-Douglas Präferenzen
beschrieben werden kann. Hier kann man die Nachfragefunktion leider nicht durch Überlegung herleiten,
sondern muß sie aus dem Nutzenmaximierungsproblem errechnen:
20
21