Präferenzen

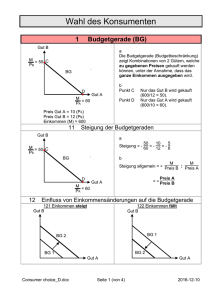
Mikroökonomie 1
Präferenzen 18.03.2010
1
Wiederholung: „ökonomische Theorie des Konsumenten“
was man sich leisten kann (Budgetrestriktion)
„die besten Dinge wählen (Präferenzen)
In der letzten Veranstaltung befassten wir uns mit
Budgetrestriktionen, d.h. was sich die Konsumentin leisten
kann.
In dieser Stunde widmen wir uns der Frage „die besten Dinge“
wählen.
Annahmen: wir haben eine vollständige Liste von Waren
und Dienstleistungen, zwischen denen die Konsumentin
wählen kann (Güterbündel)
Umstände der Nutzung bestimmen Präferenzen, z.B. Boot
in der Sahara versus Boot im Atlantik
Zur grundsätzlichen Analyse der Präferenzen: Einfaches
Entscheidungsmodell – Zwei Güterbündel
2
Präferenzen sind eine
psychologische Grösse
Präferenzen = was die Leute wollen
Präferenzen sind:
subjektiv
schwierig zu erfassen
schwierig zu messen
schlecht zwischen Personen vergleichbar
Wie entstehen sie?
3
Präferenzen können durch
Indifferenzkurven dargestellt werden
Zeichnen Sie die Indifferenzkurve zwischen inländischen und
ausländischen Tomaten.
Zeichnen Sie die Indifferenzkurve zwischen Luftverschmutzung
und Automobiltransport.
4
Annahme 1:
Monotonie der Präferenzen
Monotonie heisst: Mehr von einem Gut ist besser
Entspricht nicht „monoton“ im täglichem Sprachgebrauch.
Impliziert Unersättlichkeit
Folge: Indifferenzkurven sind negativ geneigt
Wenn ich eine zusätzliche CDs bekomme, bin ich
glücklicher.
Damit ich auf der gleichen Indifferenzkurve bleibe (also
genauso glücklich wie vorher bin) muss man mir
Kinoeintritte wegnehmen.
5
Annahme 1:
Monotonie der Präferenzen
10
8
Kinoeintritte
mehr Kinoeintritte
weniger CDs
mehr
von beidem
6
4
weniger
von beidem
2
weniger Kinoeintritte
mehr CDs
0
0
2
4
CDs
6
8
10
6
Annahme 2: Durchschnittliche
Güterkörbe sind besser als einseitige
Eine lineare Kombinationen von zwei Güterkörben A und B
sind besser als die Güterkörbe A und B.
Wichtige Annahme, weil sie die Konvexität der
Indifferenzkurven sichert.
( x1 , x 2 ) ≈ ( y1 , y2 )
( tx + ( t − 1) y , tx + ( t − 1) y ) ≥ ( x , x )
1
1
2
2
1
2
für
0 ≤ t ≤1
7
Beispiel
(2CD,8 KINO) ≈ (8CD,2 KINO )
t = 0.5
( t 2CD + (1 − t ) 8CD, t 8Kino + (1 − t ) 2Kino ) ≥ ( 2CD,8Kino )
(1CD + 4CD, 4 Kino + 1Kino ) ≥ ( 2CD,8Kino )
( 5CD,5Kino ) ≥ ( 2CD,8Kino )
8
Annahme 2: Durchschnittliche
Güterkörbe sind besser als einseitige
10
A(2,8)
Kinoeintritte
8
6
C(5,5)
4
B(8,2)
2
0
0
2
4
6
8
10
CDs
9
Annahme 2 schliesst nicht konvexe
Präferenzen aus
Wie interpretieren Sie diese Kurven?
A
x2
x2
A
C
C
B
B
x1
x1
10
Annahme 2 bedeutet:
strenge Konvexität
keine linearen Abschnitte in
sonst konvexen Kurven
x2
A
C
B
x1
11
Wieso sind diese Annahmen wichtig?
Damit wir stetige Nachfragekurven bekommen („wellbehaved“)
Für stabile Markt-Gleichgewichte.
Preis
Nachfragekurve
Menge
12
Grenzrate der Substitution GRS
GRS = MRS (marginal rate of substitution)
= Steigung der Indifferenzkurve
∆x2
−
∆x1
Nimmt
bei konvexen Indifferenzkurven ab, wenn x1
zunimmt.
Je mehr CDs man hat, auf umso weniger Kinoeintritte
ist man bereit für eine zusätzliche CD zu verzichten.
„Preis“ einer CD in Kinoeintritten => marginale
Zahlungsbereitschaft
13
Grenzrate der Substitution
x2
∆ x2
∆ x1
Steigung =
∆x2
= GRS
∆x1
x1
14
Grenzrate der Substitution
Kinoeintritte
Ausgangspunkt
besser
∆ Kinoeintritte
gleich gut
schlechter
CDs
∆ CDs
15
Die Grenzrate der Substitution
Kinoeintritte
9
∆ Kino
∆ CD
CD Kino ∆Kino
2
3
4
5
6
7
8
9
10
8.00
5.33
4.00
3.20
2.67
2.29
2.00
1.78
1.60
- 2.67
- 1.33
- 0.80
- 0.53
- 0.38
- 0.29
- 0.22
- 0.18
8
7
-2.67
6
GRS
2.67
1.33
0.80
0.53
0.38
0.29
0.22
0.18
5
+1
4
3
2
1
0
0
1
2
3
4
5
6
7
8
9
CDs
16
Grenzrate der Substitution
und Möglichkeit zu tauschen
x2
Steigung = Tauschmöglichkeit E
Das Individuum hat den Güterkorb A.
Was wird es tun, wenn es zu x1 mit x2
zum Verhältnis E tauschen kann.
A
x2
x1
x1
17
Grenzrate der Substitution
und Preis
alle anderen Güter
in Fr.
Steigung Indifferenzkurve =
Verzicht auf Fr. um eine
zusätzlich CD zu bekommen.
Steigung =
Preis einer CD in Fr.
CDs
18
Zeichnen Sie die Indifferenzkurve zwischen Forschung und
Lehrtätigkeit eines ETH-Dozenten.
1. Aus der Sicht des Dozenten.
2. Aus der Sicht eines Studierenden.
3. Zeichnen Sie die Budgetrestriktion.
19
Wie sind die Grenzraten der Substitution
- von perfekten Substituten?
- von perfekten Komplementen?
- von einem „Gut“ gegenüber einem „Schlecht“?
- von einem neutralen Gut gegenüber einem Gut?
20