Kurshalbjahr 11 - Schulbuchzentrum Online
Werbung
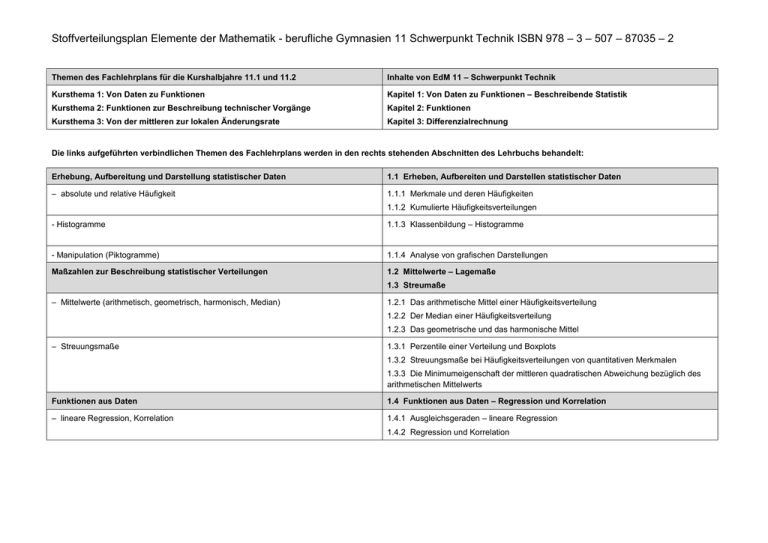
Stoffverteilungsplan Elemente der Mathematik - berufliche Gymnasien 11 Schwerpunkt Technik ISBN 978 – 3 – 507 – 87035 – 2 Themen des Fachlehrplans für die Kurshalbjahre 11.1 und 11.2 Inhalte von EdM 11 – Schwerpunkt Technik Kursthema 1: Von Daten zu Funktionen Kapitel 1: Von Daten zu Funktionen – Beschreibende Statistik Kursthema 2: Funktionen zur Beschreibung technischer Vorgänge Kapitel 2: Funktionen Kursthema 3: Von der mittleren zur lokalen Änderungsrate Kapitel 3: Differenzialrechnung Die links aufgeführten verbindlichen Themen des Fachlehrplans werden in den rechts stehenden Abschnitten des Lehrbuchs behandelt: Erhebung, Aufbereitung und Darstellung statistischer Daten 1.1 Erheben, Aufbereiten und Darstellen statistischer Daten – absolute und relative Häufigkeit 1.1.1 Merkmale und deren Häufigkeiten 1.1.2 Kumulierte Häufigkeitsverteilungen - Histogramme 1.1.3 Klassenbildung – Histogramme - Manipulation (Piktogramme) 1.1.4 Analyse von grafischen Darstellungen Maßzahlen zur Beschreibung statistischer Verteilungen 1.2 Mittelwerte – Lagemaße 1.3 Streumaße – Mittelwerte (arithmetisch, geometrisch, harmonisch, Median) 1.2.1 Das arithmetische Mittel einer Häufigkeitsverteilung 1.2.2 Der Median einer Häufigkeitsverteilung 1.2.3 Das geometrische und das harmonische Mittel – Streuungsmaße 1.3.1 Perzentile einer Verteilung und Boxplots 1.3.2 Streuungsmaße bei Häufigkeitsverteilungen von quantitativen Merkmalen 1.3.3 Die Minimumeigenschaft der mittleren quadratischen Abweichung bezüglich des arithmetischen Mittelwerts Funktionen aus Daten 1.4 Funktionen aus Daten – Regression und Korrelation – lineare Regression, Korrelation 1.4.1 Ausgleichsgeraden – lineare Regression 1.4.2 Regression und Korrelation Stoffverteilungsplan Elemente der Mathematik - berufliche Gymnasien 11 Schwerpunkt Technik ISBN 978 – 3 – 507 – 87035 – 2 Die links aufgeführten verbindlichen Themen des Fachlehrplans werden in den rechts stehenden Abschnitten des Lehrbuchs behandelt: Funktionsbegriff 2.1 Funktionsbegriff – Modellieren von Sachverhalten – Funktionsgleichung, Definitions- und Wertebereich, Darstellungen von Funktionen (enthalten in Abschnitt 2.1) Rationale Funktionen 2.2 Lineare Funktionen 2.3 Quadratische Funktionen – lineare Funktionen: Steigung / Achsenschnittpunkte / Lage zweier Geraden ( Schnitt, Orthogonalität, Parallelität) 2.2.1 Begriff der linearen Funktion – quadratische Funktionen: Eigenschaftsuntersuchungen (Nullstellen, Parameter) / Modellieren / LGS – GAUSS-Algorithmus 2.3.1 Definition – Nullstellen – Linearfaktordarstellung 2.2.2 Gegenseitige Lage von Geraden 2.3.2 Scheitelpunktform einer quadratischen Funktion – Extremwertbestimmung 2.3.3 Bestimmung quadratischer Funktionen Weitere rationale Funktionen 2.4 Ganzrationale Funktionen 2.5 Gebrochenrationale Funktionen – Nullstellenberechnung, Achsen- und Punktsymmetrie ganzrationaler Funktionen auch höheren Grades 2.4.1 Potenzfunktionen mit natürlichen Exponenten 2.4.2 Begriff der ganzrationalen Funktion 2.4.3 Globalverlauf ganzrationaler Funktionen 2.4.4 Symmetrie 2.4.5 Nullstellen ganzrationaler Funktionen – Polynomdivision – Verhalten im Unendlichen und qualitatives asymptotisches Verhalten gebrochenrationaler Funktionen 2.5.1 Potenzfunktionen mit negativen ganzzahligen Exponenten – Umkehrfunktionen (enthalten in Abschnitt 2.6.6) – abschnittsweise definierte Funktionen (enthalten in Abschnitt 2.1) – Funktionenscharen (enthalten in Abschnitt 2.3.3) Transzendente Funktionen 2.6 Exponential- und Logarithmusfunktionen 2.5.2 Eigenschaften gebrochenrationaler Funktionen 2.7 Trigonometrische Funktionen – Exponential- und Logarithmusfunktionen (insbesondere e-Funktionen und lnFunktionen), typische Kurvenverläufe 2.6.1 Exponentielles Wachstum 2.6.2 Exponentialfunktionen – Eigenschaften 2.6.3 Die EULER’sche Zahl e – Exponentialfunktionen zur Basis e 2.6.5 Lösen von Exponentialgleichungen – Logarithmus 2.6.6 Logarithmusfunktionen Stoffverteilungsplan Elemente der Mathematik - berufliche Gymnasien 11 Schwerpunkt Technik ISBN 978 – 3 – 507 – 87035 – 2 – trigonometrische Funktionen: Definition am Einheitskreis / allgemeine Sinusfunktion, Bedeutung der Parameter / Modellierung periodischer Vorgänge 2.7.1 Sinus, Kosinus und Tangens im rechtwinkligen Dreieck – Wiederholung 2.7.2 Sinus und Kosinus am Einheitskreis 2.7.3 Bogenmaß eines Winkels 2.7.4 Definition und Eigenschaften der Sinusfunktion 2.7.5 Strecken des Graphen der Sinus- und Kosinusfunktion 2.7.6 Verschieben der Graphen der Sinus- und Kosinusfunktion 2.7.7 Allgemeine Sinusfunktion 2.7.8 Modellieren mit allgemeinen Sinusfunktionen – Anwendungen Die links aufgeführten verbindlichen Themen des Fachlehrplans werden in den rechts stehenden Abschnitten des Lehrbuchs behandelt: Änderungsraten 3.1 Tangentensteigung und Änderungsraten – Ableitung – mittlere Änderungsrate, Differenzenquotient, Sekantensteigung 3.1.1 Steigung eines Funktionsgraphen in einem Punkt – Ableitung – lokale Änderungsrate, Differentialquotient als Grenzwert des Differenzenquotienten, Tangentensteigung 3.1.2 Lokale Änderungsrate Ableitungsfunktion, Ableitungsregeln 3.2 Differenzierbarkeit – Ableitungsfunktion 3.3 Ableitungsregeln Zusammenhang zwischen Funktion und Ableitungsfunktion 3.1.3 Ableitung der Quadratfunktion 3.1.4 Ableitung weiterer Funktionen 3.2.1 Differenzierbarkeit 3.2.2 Ableitungsfunktion – Faktorregel, Summenregel, Potenzregel 3.2.3 Ableitung der Potenzfunktionen – Potenzregel 3.3.1 Faktorregel 3.3.2 Summenregel Stoffverteilungsplan Elemente der Mathematik - berufliche Gymnasien 11 Schwerpunkt Technik ISBN 978 – 3 – 507 – 87035 – 2 Hinweise zur Umsetzung des Fachlehrplans Kursthema 1 Realisation in EdM 11 Technik Häufigkeitsverteilungen: z. B. Produktionsdaten / -prozesse enthalten in verschiedenen Abschnitten des Kapitels 1 Mittelwerte: z. B. Wachstumsprozesse, Geschwindigkeiten, Dichten enthalten in Abschnitt 1.2.3 Das geometrische und das harmonische Mittel Regression: z. B. HOOKE’sches Gesetz enthalten in den Abschnitten 1.4.1 Ausgleichsgeraden – lineare Regression Quadratische Regression in Abschnitt 2.3.3 Bestimmung quadratischer Funktionen Kubische Regression in Abschnitt 2.4.2 Begriff der ganzrationalen Funktion 2.6.4 Exponentielle Regression Hinweise zur Umsetzung des Fachlehrplans Kursthema 2 Realisation in EdM 11 Technik Funktionsbegriff: technische Anwendungsbeispiele enthalten in den Abschnitten zu den einzelnen Funktionstypen, insbesondere in Lineare Funktionen: z. B. Weg-Zeit-Gesetz, Ohmsches Gesetz Abschnitt 2.5.3 Rationale Funktionen in technischen Zusammenhängen Quadratische Funktionen: z. B. Wurfparabeln, Brennpunkteigenschaft, gleichmäßig beschleunigte Bewegung, idealisierter freier Fall, Ablenkung geladener Teilchen im homogenen E-Feld, Brückenbau Brennpunkteigenschaft behandelt in Abschnitt 3.1.3 Ableitung der Quadratfunktion – Brennpunkteigenschaft Eigenschaften ganzrationaler Funktionen: z. B. Konturlinie einer Karosserie, Kostenfunktion Gebrochenrationale Funktionen: z. B. Potentiale, Linsengleichung, Verkehrsdichte Exponential- und Logarithmusfunktionen: z. B. Lade- und Entladevorgänge, lineare und exponentielle Wachstumsvorgänge, Zerfallsprozesse, barometrische Höhenformel, Dezibel (Akustik) enthalten in den Abschnitten trigonometrische Funktionen: z. B. Drehkolben, Wechselspannung, Schwingungen, Ebbe und Flut insbesondere enthalten in Abschnitt 2.7.8 Modellieren mit allgemeinen Sinusfunktionen – Anwendungen 2.6.4 Exponentielle Regression 2.6.7 Exponential- und Logarithmusfunktionen in technischen Anwendungen Stoffverteilungsplan Elemente der Mathematik - berufliche Gymnasien 11 Schwerpunkt Technik ISBN 978 – 3 – 507 – 87035 – 2 Hinweise zur Umsetzung des Fachlehrplans Kursthema 3 Realisation in EdM 11 Technik Änderungsrate: z. B. durchschnittliche Geschwindigkeit, Momentangeschwindigkeit zur Veranschaulichung der lokalen / punktuellen Änderungsrate enthalten in den Abschnitten 3.1 und 3.2, insbesondere in Abschnitt 3.4 Differenzialrechnung in technischen Anwendungen Ableitungsfunktion: z. B. Weg – Geschwindigkeit, Arbeit – Leistung, Ladung – Stromstärke Hinweise zur Umsetzung des Fachlehrplans: Werkzeuge Realisation in EdM 11 Technik Hilfsmittel: Computeralgebrasystem (CAS), Tabellenkalkulation, Funktionsplotter und / oder internetbasierte Applets Verweise auf den Einsatz der Werkzeuge enthalten in verschiedenen Abschnitten