Mengen und Aussagen

2 ck / hiebaum
Aussagenlogik und Mengen
September 2010
Teil 1: Aussagenlogik
Was ist eine Aussage?
Eine Aussage ist eine Behauptung, die nur wahr oder
falsch sein kann (Zweiwertige Logik). Jeder Aussage
(Argument) wird ein Wahrheitswert zugeordnet.
Was ist eine Aussageform?
Aussageformen sind Aussagen, in deren
Formulierungen sogenannte Variable vorkommen
dürfen. Erst durch die Belegung der Variablen durch
Werte, bzw. Prädikate wird eine Aussageform zu einer
Aussage.
Kann man Aussage verknüpfen?
ja, es gibt: Negation, Konjunktion, Disjunktion,
Implikation und Äquivalenz.
Was ist die Negation?
Verneinung oder Negation:
A
(„nicht A“)
bzw. NICHT(A) (in Excel)
A ist genau dann wahr, wenn A falsch ist und
umgekehrt.
Dreht den Wahrheitswert einer Aussage um.
Was ist die Konjunktion?
(„A und B“) bzw.
AB
UND(A;B)
liefert nur dann den Wahrheitswert wahr, wenn beide
Aussagen wahr sind.
Was ist die Disjunktion?
A  B („A oder B“)
bzw. ODER(A;B)
liefert nur dann den Wahrheitswert falsch, wenn beide
Aussagen falsch sind.
Was ist die Implikation?
A  B („aus A folgt B“)
A ist hinreichend für B, B ist notwendig für A
liefert nur dann den Wahrheitswert falsch, wenn A
wahr und B falsch ist.
Was ist eine Äquivalenz?
A  B („A ist gleichwertig oder äquivalent mit
B“)
A ist hinreichend und notwendig für B
liefert den Wahrheitswert wahr, wenn A und B gleiche
Wahrheitswerte haben.
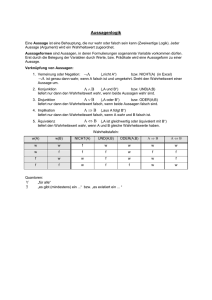
Wahrheitstafeln:
w(A)
w(B)
NICHT(A)
UND(A;B)
ODER(A;B)
AB
AB
w
w
f
w
w
w
w
w
f
f
f
w
f
f
f
w
w
f
w
w
f
f
f
w
f
f
w
w
© wolfgang streit
seite 1 von 10
2 ck / hiebaum
Aussagenlogik und Mengen
September 2010
Was sind Quantoren?
 „für alle“
 „es gibt (mindestens) ein ...“ bzw.
„es existiert ein ... “
Beispiel 1:
Bilden Sie die Wahrheitstafel für (A  B).
Beispiel 2:
Bilden Sie die Wahrheitstafel für A  (B  C)
Beispiel 3:
Wie kann man A  B durch andere Verknüpfungen darstellen?
© wolfgang streit
seite 2 von 10
2 ck / hiebaum
Aussagenlogik und Mengen
September 2010
Teil 2: Mengen
Was ist eine Menge?
Eine Menge ist eine Zusammenfassung von
bestimmten wohlunterschiedenen Objekten unserer
Anschauung oder unseres Denkens zu einem
Ganzen. Die Objekte heißen Elemente der Mengen.
Schreibweise:
x A
x A
 x E x
x ist Element von A
x ist kein Element von A
x aus A
x nicht aus A
Menge aller Elemente x, die die
Eigenschaft E haben
Menge aller x, für die gilt:
Wann sind zwei Mengen gleich?
Mengen sind gleich, wenn sie die gleichen Elemente
haben.
Was ist die Mächtigkeit einer Menge?
Die Anzahl der Elemente einer Menge A heißt
Mächtigkeit oder Kardinalzahl von A.
card(A) oder A
Beispiel 4:
Stellen sie aufzählend dar: A = {x (x ist eine gerade Zahl)  (x < 10)}. Wie groß ist card(A)?
Beispiel 5:
Stellen Sie die Menge B = {10, 20, 30, 100, 200} beschreibend dar.
Was ist die leere Menge?
Die leere Menge { } bzw  hat keine Elemente.
Was ist eine Teilmenge?
A ist Teilmenge von B, wenn alle Elemente von A
auch Elemente von B sind.
A  B  x  A  x  B
Was ist ein Venn-Diagramm?
Ein Venndiagramm ist die grafische Darstellung einer
Menge als Teilmenge der Zeichenebene.
Beispiel 6:
Stellen Sie folgende Bereiche (Elemente sind die einzelnen Zellen) in einem Spread-sheet als
Venndiagramm dar:
A = B2:E7
B = C4:D9
C = D5:E6
Wie groß sind die Kardinalzahlen dieser Mengen? Welche Menge ist Teilmenge von welcher anderen
Menge?
© wolfgang streit
seite 3 von 10
2 ck / hiebaum
Aussagenlogik und Mengen
September 2010
Was ist die Potenzmenge?
Die Potenzmenge einer Menge A ist die Menge aller
Teilmengen von A.
Beispiel 7:
Ermitteln Sie die Potenzmenge von D = {1, 2, 3}
Was ist die Komplementärmenge?
Die Rest- oder Komplementärmenge enthält genau
jene Elemente von A, die nicht zu B gehören.
„ A minus B“
A \ B:  x x  A  x  B
Was ist die Durchschnittsmenge?
Die Durchschnittsmenge zweier Mengen A und B
enthält nur jene Elemente, die sowohl in A als auch in
B enthalten sind.
„A geschnitten mit B“
A  B:  x x  A  x  B
„A und B“
in EXCEL ist der Schnittmengenoperator das
Leerzeichen: Bereich1 Bereich2
Was ist die Vereinigungsmenge?
Die Vereinigungsmenge zweier Mengen A und B
enthält alle Elemente die zu A oder B gehören.
A vereinigt mit (oder) B“
„A oder B“
A  B:  x x  A  x  B
in EXCEList der Vereinigungsoperator der Strichpunkt:
Bereich1:Bereich2
Beispiel 8:
Bilden Sie aus den Mengen A = {1, … 9}, B = {2, 3, 5, 7} und C = {1, 5, 7, 10} die Menge
A \ (B  C).
Beispiel 9:
Zeichnen Sie ein allgemeines Venndiagramm mit 3 Mengen A, B und C, so dass alle Schnittmengen
nicht leer sind und schraffieren Sie den Bereich (A  B) \ C.
© wolfgang streit
seite 4 von 10
2 ck / hiebaum
Aussagenlogik und Mengen
September 2010
Beispiel 10:
In einer Gruppe von Leuten können 50 Leute Englisch, 30 Spanisch und 40 Französisch. Niemand
kann keine Fremdsprache. 15 Leute sprechen alle drei Sprachen. 25 können Spanisch und
Französisch, 11 nur Französisch. 28 Leute können nur Englisch. Stellen Sie die Situation im
Venndiagramm dar und ermitteln Sie, wie groß die Gruppe ist.
Teil 3: Zahlenmengen
Was ist die Menge der natürlichen Zahlen?
(set of natural numbers)
N = {0, 1, 2, …}
Es gibt keine größte natürliche Zahl, jede natürliche
Zahl hat einen Nachfolger,der um 1 größer ist als diese
Zahl.
Die Mächtigkeit von N heißt Aleph 0 0
N ist abgeschlossen bzgl. Addition und Multiplikation,
d.h. wenn man zwei natürliche Zahlen addiert bzw.
multipliziert, ist das Ergebnis wieder aus N.
Das neutrale Element bzgl. Addition ist 0 und bzgl
Multiplikation ist 1
Was ist die Menge der ganzen Zahlen?
(set of integer numbers)
Z = {…, –2, –1, 0, 1, 2, …}
Negative Zahlen sind als inverse Elemente von
positiven Zahlen bzgl. der Addition definiert:
a + (–a) = 0
Die Mächtigkeit von N heißt Aleph 0 0
Z ist abgeschlossen bzgl. Addition und Multiplikation,
es gibt aber kein inverses Element bzgl. der
Multiplikation (d.h. man kann nicht Dividieren)
card (Z) = 0
d.h. es gibt gleich viele ganze wie natürliche Zahlen.
Rechenregeln:
a + a = 2a
a + (–a) = a – a = 0
a – (+a) = a – a = 0
a – (–a) = a + a = 2a
a · a = a2
a · (–a) = – a2
(–a) · a = – a2
(–a) · (–a) = a2
© wolfgang streit
seite 5 von 10
2 ck / hiebaum
Aussagenlogik und Mengen
September 2010
Was ist die Menge der rationalen Zahlen?
(set of rational numbers)
Q = {x = Error!(z  Z)  (n  Z \ {0} }
Q ist die Menge aller Brüche, z heißt Zähler, n
Nenner
Brüche mit z =1 sind als inverse Elemente von
ganzen Zahlen bzgl. der Multiplikation definiert:
Error! · n = 1
ganze Zahlen sind Brüche mit n = 1
Der Nenner eines Bruches darf nicht Null sein.
Q ist abgeschlossen bzgl. Addition und
Multiplikation, es gibt für jedes Element außer 0 ein
inverses Element bzgl. der Multiplikation
card (Q) = 0
d.h. es gibt gleich viele rationale wie natürliche
Zahlen.
es gelten die gleichen Vorzeichenregeln wie in Z
Darstellung:
als Bruch oder
als endliche oder unendlich periodische
Dezimalzahl
Gibt es irrationale Zahlen?
ja, z. Bsp alle Wurzeln, die nicht ganzzahlig sind
und jede Menge anderer Zahlen, es gibt mehr
irrationale Zahlen wie rationale.
Beispiele:
die Länge der Diagonale in einem Quadrat mit der
Seitenlänge 1 = 2  Q
das Verhältnis von Umfang zum Durchmesser
eines Kreises =   3,14159…
die unendliche Summe
1 + Error! + Error! + Error! + Error! + … = e
e heißt Eulersche Zahl.
e und  sind Beispiele für irrational transzendente
Zahlen, d.h. sind können weder als Bruch noch als
Wurzel angeschrieben werden.
Was sind reelle Zahlen?
(set of real numbers)
Vereinigt man die rationalen mit den irrationalen
Zahlen, dann entsteht die Menge der reellen Zahlen R
Beinahe jede Rechenoperation in R ist möglich!
Ausnahme:
Division durch 0
Wurzel aus einer negativen Zahl
Was ist ein reelles Intervall?
Das geschlossene Intervall
[a / b ] = {x (x  R) )  (a  x  b) }
© wolfgang streit
seite 6 von 10
2 ck / hiebaum
Aussagenlogik und Mengen
September 2010
dh. das sind alle reellen Zahlen zwischen a und b,
wobei a und b zum Intervall gehören
Das offene Intervall
(a / b ) = {x (x  R) )  (a < x < b) }
dh. das sind alle reellen Zahlen zwischen a und b,
wobei a und b nicht zum Intervall gehören
© wolfgang streit
seite 7 von 10
2 ck / hiebaum
Aussagenlogik und Mengen
September 2010
Struktur der Zahlenmengen
Reelle Zahlen
R
Rationale Zahlen
Q
Brüche
Irrationale Zahlen
algebraisch
Wurzeln
echte Brüche
negative
Zahlen
© wolfgang streit
transzendent
e,
Ganze Zahlen
Z
Natürliche Zahlen
N
seite 8 von 10
2 ck / hiebaum
Aussagenlogik und Mengen
September 2010
Lösungen
Beispiel 1:
Bilden Sie die Wahrheitstafel für (A  B).
A
w
w
f
f
B
w
f
w
f
B
f
w
f
w
A  B
w
w
f
w
(A  B)
f
f
w
f
Beispiel 2:
Bilden Sie die Wahrheitstafel für A  (B  C)
A
1
1
1
1
0
0
0
0
B
1
1
0
0
1
1
0
0
C
1
0
1
0
1
0
1
0
BC
1
0
0
0
1
0
0
0
A  (B  C)
1
0
0
0
1
1
1
1
Beispiel 3:
Wie kann man A  B durch andere Verknüpfungen darstellen?
A
w
w
f
f
B
w
f
w
f
A
f
f
w
w
A  B
w
f
w
w
AB
w
f
w
w
also: (A  B)  (A  B)
Beispiel 4:
Stellen sie aufzählend dar: A = {x (x ist eine gerade Zahl)  (x < 10)}. Wie groß ist card(A)?
A = {2, 4, 6, 8}
card(A) = 4
Beispiel 5:
Stellen Sie die Menge B = {10, 20, 30, 100, 200} beschreibend dar.
B = {x ((x ist ohne Rest durch 10 teilbar)  (x  30)) 
((x ist ganzzahlig durch 100 teilbar)  (x < 300))}
Beispiel 6:
Stellen Sie folgende Bereiche (Elemente sind die einzelnen Zellen) in einem
Spread-sheet als Venndiagramm dar:
A = B2:E7
B = C4:D9
C = D5:E6
Wie groß sind die Kardinalzahlen dieser Mengen? Welche Menge ist
Teilmenge von welcher anderen Menge?
card(A) = 24 card(B) = 12 card(C) = 4
© wolfgang streit
CA
seite 9 von 10
2 ck / hiebaum
Aussagenlogik und Mengen
September 2010
Beispiel 7:
Ermitteln Sie die Potenzmenge von D = {1, 2, 3}
P(D) = { {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3} }
Beispiel 8:
Bilden Sie aus den Mengen A = {1, … 9}, B = {2, 3, 5, 7} und C = {1, 5, 7, 10} die Menge
A \ (B  C).
A \ (B  C) = A \ {1, 2, 3, 5, 7, 10} = {4, 6, 8, 9}
Beispiel 9:
Zeichnen Sie ein allgemeines Venndiagramm mit 3 Mengen A, B und C,
so dass alle Schnittmengen nicht leer sind und schraffieren Sie den
Bereich (A  B) \ C.
Beispiel 10:
In einer Gruppe von Leuten können 50 Leute Englisch, 30
Spanisch und 40 Französisch. Niemand kann keine
Fremdsprache. 15 Leute sprechen alle drei Sprachen. 25
können Spanisch und Französisch, 11 nur Französisch. 28
Leute können nur Englisch. Stellen Sie die Situation im
Venndiagramm dar und ermitteln Sie, wie groß die Gruppe ist.
Es sind ingesamt
28 + 3 + 4 + 15 +2 + 10 + 11 =
73 Personen.
© wolfgang streit
seite 10 von 10