Lineare Funktionen - Gymnasium "Am Thie"

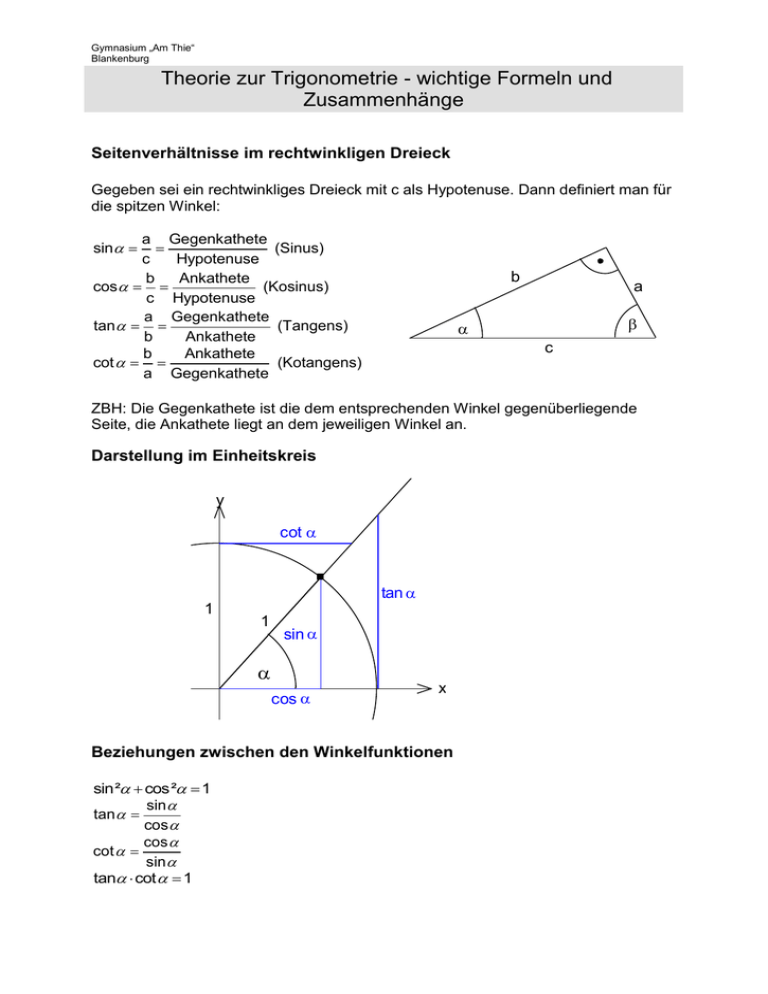
Gymnasium „Am Thie“
Blankenburg
Theorie zur Trigonometrie - wichtige Formeln und
Zusammenhänge
Seitenverhältnisse im rechtwinkligen Dreieck
Gegeben sei ein rechtwinkliges Dreieck mit c als Hypotenuse. Dann definiert man für
die spitzen Winkel:
a Gegenkathete
(Sinus)

c
Hypotenuse
b
Ankathete
(Kosinus)
cos  
c Hypotenuse
a Gegenkathete
tan  
(Tangens)
b
Ankathete
b
Ankathete
(Kotangens)
cot   
a Gegenkathete
sin 
b
a
b

c
ZBH: Die Gegenkathete ist die dem entsprechenden Winkel gegenüberliegende
Seite, die Ankathete liegt an dem jeweiligen Winkel an.
Darstellung im Einheitskreis
y
cot 
tan 
1
1
sin 

cos 
x
Beziehungen zwischen den Winkelfunktionen
sin²  cos²  1
sin
tan 
cos 
cos 
cot  
sin
tan  cot   1
Gymnasium „Am Thie“
Blankenburg
Theorie zur Trigonometrie - wichtige Formeln und
Zusammenhänge
Besondere Werte der Winkelfunktionen

sin
cos
tan
cot 
0°
0
1
0

30°
1
2
1
 3
2
1
3
3
3
45°
1
 2
2
1
 2
2
1
1
60°
1
 3
2
1
2
3
90°
1
3
3
0
1
0

Funktionen der Komplementwinkel
sin  cos(90   )
tan  cot(90   )
cos   sin(90   )
cot   tan(90   )
Funktionswerte in den Quadranten
tan 
cot 
cos 
sin 
+
+
-
+
-
+
-
-
-
+
+
-
Vorzeichen der Funktionswerte für Winkel > 90° und für negative Winkel
2. Quadrant
3. Quadrant
sin  sin(180   )
4. Quadrant
tan   tan(180   )
cos   cos(180   )
cot    cot(180   )
sin   sin(  180) negative Winkel
tan  tan(  180)
cos   cos(  180)
cot   cot(  180)
Flächeninhaltssatz (für beliebige Dreiecke gültig)
A
1
1
1
ab  sin   ac  sin b  bc  sin 
2
2
2
sin   sin(360   )
tan   tan(360   )
cos  cos(360   )
cot    cot(360   )
sin(  )   sin
tan(  )   tan
cos(  )  cos
cot(  )   cot 
Gymnasium „Am Thie“
Blankenburg
Theorie zur Trigonometrie - wichtige Formeln und
Zusammenhänge
Es geht weiter mit etwas spezielleren Dingen für Freunde der Mathematik…
Summenformeln
sin(  ß)  sin cosß  cos  sinß
tan  tanß
tan(  ß) 
1 tan tanß
cos(  ß)  cos cosß sin sinß
cot  cotß 1
cot(  ß) 
cotß  cot 
Sonderfälle:
sin2  2sin cos
2 tan
tan2 
1  tan ²
cos2  cos²  sin²

sin
tan 
2 1  cos 
Umrechnung Grad/Minuten/Sekunden in Dezimalgrad
Beispiel
16° 19' 28,29" (sprich 16 Grad 19 Minuten 28,29 Sekunden) sind wie viel Dezimalgrad?
Lösung
Sekunden durch 60 dividieren (28,29/60 = 0,4715)
Minuten addieren (0,4715 + 19 = 19,4715)
Ergebnis durch 60 dividieren (19,4715 / 60 = 0,34525)
Gradzahl addieren (0,34525 + 16 = 16,34525)
Ergebnis: 16° 19' 28,29" = 16,324525°
Umrechung Dezimalgrad in Grad/Minuten/Sekunden
Beispiel
48,177455556° (Dezimalgrad) sind wie viel Grad, Minuten, Sekunden?
Lösung
Der ganzzahlige Anteil sind Grad: 48
Davon den Nachkommaanteil mit 60 multiplizieren, der ganzzahlige Anteil sind Minuten: 10
Davon wiederum den Nachkommaanteil mit 60 multiplizieren, sind Sekunden: 38,84
Ergebnis: 48,177455556° = 48° 10' 38,84"