Produktionstheorie

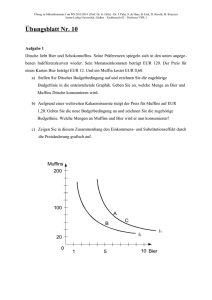
Produktionstheorie
Sie haben bisher kennen gelernt: die Produktion des Unternehmens in
Mengeneinheiten und mit Preisen bewertet
Wir wiederholen nochmals zur Einführung in die Produktionstheorie ein Beispiel mit
einer Minimalkostenkombination. Anschließend untersuchen wir auf
volkswirtschaftlicher Ebene die Einsatzrelationen von Arbeit und Kapital.
Vergleichen wir zwei Minimalkostenkombinationen für zwei Einsatzfaktoren.
Minimalkostenkombination.PPT
q2
K
p2
E0
E1
K
p1
K
p1 '
q1
Wie wirkt sich eine Preiserhöhung für einen Faktor auf die Einsatzmenge aus....?
Analog zur Haushaltstheorie: die Isokostenlinie dreht sich um den Anteil des
konstanten Faktors (im Schnittpunkt mit der Ordinate). Bei gegebenem Kostenplan
kann bei einer Kostensenkung des Faktors p1 nun mehr von diesem Faktor gekauft
und eingesetzt werden. Die geringere Steigung drückt das veränderte Preisverhältnis
an dem Gleichgewichtspunkt E1 aus. Die Faktoren werden nach ihren

p
Preisverhältnissen 1 eingesetzt. Wie das beschrieben wird, werden wir jetzt am
p2
Beispiel und in der Algebra sehen.
Erinnern wir uns nochmals an die Grenzrate der Substitution. Sie gibt die Änderung
der Einsatzverhältnisse entlang der substitutiven Produktionsfunktion an, also:

q1
. Wir schauen uns das am einfachen Beispiel an: Excel Nutzengebirge3.
q2
Für die folgenden Betrachtungen werden wir die Mengen mit den Preisen bewerten,
denn in der Ökonomie kommt es auf die Kostenfolgen der Mengenänderung an.
VWL 3. Version
SS 2006
Seite 1
Mit Preisen schreibt sich der Quotient so:
 q1  p1
Ersparnis  q1 p1

 q2  p2 Mehrausgab e  q2 p2
Das Optimum ist an der Stelle zu finden, wo die Einsparung bei q1 gleich der
Mehrausgabe bei q2 ist. Das schreibt man:
q1
p
 2
q 2
p1
q1  p1  q2  p2 und kann schlussfolgern:
Die Faktormengen werden also verändert, bis ihr Verhältnis den relativen Preisen
entspricht.
Jetzt beziehen wir das Ganze noch auf den Output. Die Veränderung des Output bei
einer Veränderung der Einsatzmenge haben wir definiert als...? die
Grenzproduktivität eines Faktors. Wir erhalten Sie mit einer Erweiterung unserer
Funktion um die Outputdifferenz:
q1  O p2
O O p 2
und umgeformt:



q2  O p1
q 2 q1 p1
Das Kostenminimum ist dann erreicht, wenn die Preisrelation der Einsatzfaktoren
dem Verhältnis der Grenzproduktivitäten entspricht. Ein relativ teurerer Faktor muss
eine entsprechend höhere Grenzproduktivität mitbringen. (Beim Haushalt: der relativ
teurere Kauf muss einen höheren Nutzen stiften.)
Der Kölsche sagt dafür: Wat kos et un wat bring et?
Betrachten wir das an dem konkreten Beispiel der Volkswirtschaft mit zwei
Isoquanten für zwei Zeitpunkte:
Minimalkosten/Volkswirtschaftliche Substitution
Beschäftigte
In Mio.
Y95 =2.350 Mrd DM
28
20
Y60=920 Mrd. DM
4
VWL 3. Version
15
SS 2006
Kapitalstock
in Bill. DM
Seite 2
Man stellt eine Substitution fest, warum ...?
Der Kapitalstock hat sich von 1960 bis 1995 ungefähr vervierfacht, während die Zahl
der Beschäftigten nur um ein Viertel gewachsen ist. Die Arbeit hat sich in
Deutschland sehr viel stärker verteuert, als der Preis des Kapitals. Wenn die
Lohnerhöhungen über die Grenzproduktivität der Arbeit steigen, führen sie zu einer
Substitution der Arbeit durch Kapital.
Das Ergebnis ist ökonomisch dadurch erklärbar, dass die Unternehmen gemäß der
Kostenminimierungsregel das Faktoreinsatzverhältnis zu Lasten der Arbeit
verschoben haben. Das Modell ist stark vereinfacht. So fehlt zum Beispiel der
Einfluss des technischen Fortschritts oder der Außenwirtschaft und anderer
Rahmenbedingungen.
Das Beispiel zeigt uns eine gesamtwirtschaftliche Produktionsfunktion.
Die Produktionsfunktion beschreibt die Abhängigkeit des Output von der Menge des
Faktoreinsatzes.
Die Kostenfunktion zeigt, wie sich die Kosten in Abhängigkeit von der Höhe der
Produktion entwickeln.
Die Verbindung der beiden Begriffe wird über die Minimalkostenkombination
hergestellt. (Minimalkostenkombination/Minimalkostenlinie.PPT)
VWL 3. Version
SS 2006
Seite 3