Volumenberechnungen

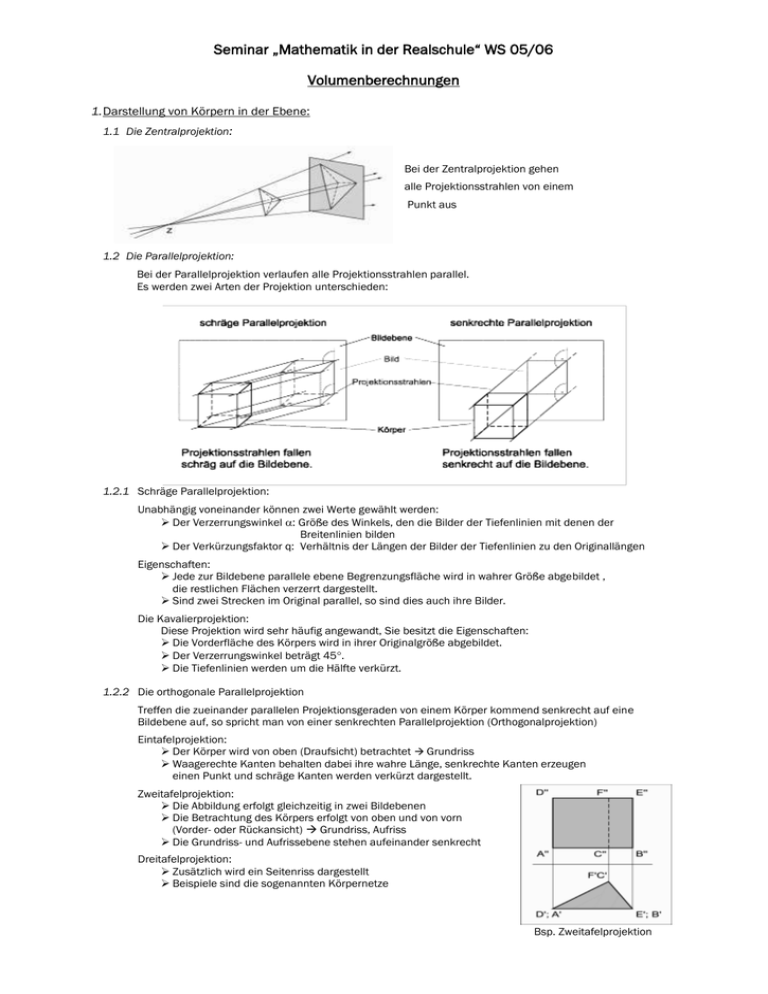
Seminar „Mathematik in der Realschule“ WS 05/06
Volumenberechnungen
1. Darstellung von Körpern in der Ebene:
1.1 Die Zentralprojektion:
Bei der Zentralprojektion gehen
alle Projektionsstrahlen von einem
Punkt aus
1.2 Die Parallelprojektion:
Bei der Parallelprojektion verlaufen alle Projektionsstrahlen parallel.
Es werden zwei Arten der Projektion unterschieden:
1.2.1 Schräge Parallelprojektion:
Unabhängig voneinander können zwei Werte gewählt werden:
 Der Verzerrungswinkel : Größe des Winkels, den die Bilder der Tiefenlinien mit denen der
Breitenlinien bilden
 Der Verkürzungsfaktor q: Verhältnis der Längen der Bilder der Tiefenlinien zu den Originallängen
Eigenschaften:
 Jede zur Bildebene parallele ebene Begrenzungsfläche wird in wahrer Größe abgebildet ,
die restlichen Flächen verzerrt dargestellt.
 Sind zwei Strecken im Original parallel, so sind dies auch ihre Bilder.
Die Kavalierprojektion:
Diese Projektion wird sehr häufig angewandt, Sie besitzt die Eigenschaften:
 Die Vorderfläche des Körpers wird in ihrer Originalgröße abgebildet.
 Der Verzerrungswinkel beträgt 45.
 Die Tiefenlinien werden um die Hälfte verkürzt.
1.2.2 Die orthogonale Parallelprojektion
Treffen die zueinander parallelen Projektionsgeraden von einem Körper kommend senkrecht auf eine
Bildebene auf, so spricht man von einer senkrechten Parallelprojektion (Orthogonalprojektion)
Eintafelprojektion:
 Der Körper wird von oben (Draufsicht) betrachtet  Grundriss
 Waagerechte Kanten behalten dabei ihre wahre Länge, senkrechte Kanten erzeugen
einen Punkt und schräge Kanten werden verkürzt dargestellt.
Zweitafelprojektion:
 Die Abbildung erfolgt gleichzeitig in zwei Bildebenen
 Die Betrachtung des Körpers erfolgt von oben und von vorn
(Vorder- oder Rückansicht)  Grundriss, Aufriss
 Die Grundriss- und Aufrissebene stehen aufeinander senkrecht
Dreitafelprojektion:
 Zusätzlich wird ein Seitenriss dargestellt
 Beispiele sind die sogenannten Körpernetze
Bsp. Zweitafelprojektion
2. Volumenberechnungen verschiedener räumlicher Körper
2.1 Das gerade n-seitige Prisma
Volumen = Grundfläche x Höhe
VPr isma  A G  h
2.1.1 Spezialfall Quader:
Ein Quader ist ein gerades Prisma mit paarweise kongruenten Rechtecksflächen
Volumen = Länge x Breite x Höhe
= Grundfläche
VQuader  a  b  c
2.1.2 Spezialfall Würfel:
Ein Würfel ist ein spezieller Quader und gehört zu den vierseitigen Prismen
mit rechtwinklig aufeinander stehenden Kanten.
Ein Würfel besitzt sechs zueinander kongruente Quadrate als Begrenzungsflächen,
die paarweise zueinander parallel liegen.
Volumen = Länge x Breite x Höhe
= Grundfläche
VWürf el  a  a  a  a3
2.2 Die gerade und schiefe Pyramide

Siehe Unterrichtsstunde

Exkurs: Der Satz des Cavalieri
FRANCESCO BONAVENTURA CAVALIERI, ein Schüler GALILEIs, veröffentlichte 1629 das auf seinen
Überlegungen beruhende Prinzip des Volumenvergleichs zweier Körper.
Liegen zwei Körper zwischen zwei parallelen Ebenen und sind die Inhalte der Schnittflächen der
Körper mit jeder zur Grundfläche parallelen Ebene einander gleich, so haben diese Körper auch das
gleiche Volumen.

Eine weitere Möglichkeit zur Herleitung der Volumenformel von Pyramiden
2.3 Rotationskörper
2.3.1 Der gerade Kreiszylinder
Ein Kreiszylinder ist ein Körper mit zwei kongruenten und parallelen Kreisen als
Grund- und Deckfläche.
Er entsteht durch Rotation eines Rechtecks um eine seiner Seiten
Volumen = Grundfläche x Höhe
VZy linder  A G  h  r 2  h
2.3.2 Der Kreiskegel
Werden alle Punkte eines Kreises mit einem Punkt S außerhalb
der Kreisebene
verbunden, so schließen diese Strecken gemeinsam mit dem Kreis einen Körper
ein, der Kreiskegel
Ein Kreiskegel entsteht durch Rotation eines rechtwinkligen Dreiecks um
eine seiner Katheten
Volumen = 1/3 Grundfläche x Höhe
VKegel 
1
1
A G  h  r 2
3
3
2.3.3 Die Kugel
Die Kugel ist die Menge aller Punkte des Raums, die von einem festen Punkt M, dem
Mittelpunkt der Kugel, den gleichen Abstand r haben. Der Abstand heißt Radius der
Kugel.
Sie entsteht, wenn ein Halbkreis um seinen Durchmesser rotiert. Der
Kreismittelpunkt ist zugleich Kugelmittelpunkt.
Zur Herleitung der Formel für das Volumen einer Kugel kann nach einer Idee von GALILEI
ein Körper geschaffen werden, der in gleichen Höhen den gleichen Querschnitt wie eine Halbkugel hat. Ein solcher
Körper entsteht, wenn man aus einem Kreiszylinder mit dem Grundflächenradius r und der Höhe r einen Kreiskegel mit
gleicher Grundfläche und gleicher Höhe herausschneidet (Bild 1).
Werden dieser Restköper und eine Halbkugel mit dem gleichen Radius r in der gleichen Höhe x durch eine Ebene
geschnitten, haben die Schnittflächen den gleichen Flächeninhalt, wie die folgende Überlegung an einem Schnitt durch
beide Körper zeigt (Bild 2).
Bild 1: Halbkugel mit Schnittfläche
Bild 2: Schnitt durch Körper
Da das hervorgehobene Dreieck gleichschenklig ist, gilt:
r1  x
Für den Flächeninhalt A1 des Kreisringes ergibt sich demzufolge:

A 1  r 2   r1   r 2   x 2    r 2  x 2
2

Nach dem Satz des PYTHAGORAS gilt für die Halbkugel

A 2  r2    r 2  x 2
2
;
also ist
r 2  x 2  r2
2
und deshalb
A1  A 2 .
Nach dem Satz des CAVALIERI gilt dann
VHalbkugel  VZy linder  VKegel  r 2   h 
und folglich gilt für das Volumen einer Kugel:
VKugel 
4 3
r 
3
1 2
2
2
r   h  r 2  h  r 3
3
3
3
Literaturverzeichnis:
 DUDEN-Mathematik Basiswissen Schule;Hrsg. G.Rolles, M.Unger; PAETEC verlag f.Bildungsmedien
 Handbuch Mathematik; W.Scholl, R. Drews; FALKEN Verlag