Lineare Funktionen - Gymnasium "Am Thie"

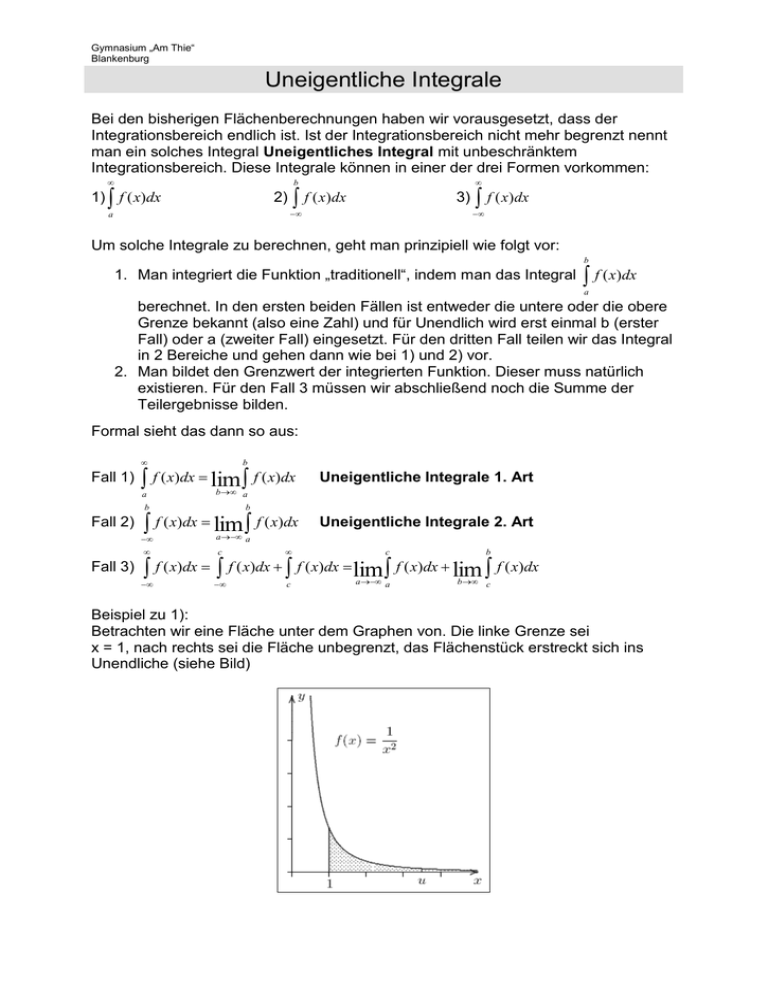
Gymnasium „Am Thie“
Blankenburg
Uneigentliche Integrale
Bei den bisherigen Flächenberechnungen haben wir vorausgesetzt, dass der
Integrationsbereich endlich ist. Ist der Integrationsbereich nicht mehr begrenzt nennt
man ein solches Integral Uneigentliches Integral mit unbeschränktem
Integrationsbereich. Diese Integrale können in einer der drei Formen vorkommen:


b
1)  f ( x)dx
2)

3)
f ( x) dx

a
 f ( x)dx

Um solche Integrale zu berechnen, geht man prinzipiell wie folgt vor:
b
1. Man integriert die Funktion „traditionell“, indem man das Integral
 f ( x)dx
a
berechnet. In den ersten beiden Fällen ist entweder die untere oder die obere
Grenze bekannt (also eine Zahl) und für Unendlich wird erst einmal b (erster
Fall) oder a (zweiter Fall) eingesetzt. Für den dritten Fall teilen wir das Integral
in 2 Bereiche und gehen dann wie bei 1) und 2) vor.
2. Man bildet den Grenzwert der integrierten Funktion. Dieser muss natürlich
existieren. Für den Fall 3 müssen wir abschließend noch die Summe der
Teilergebnisse bilden.
Formal sieht das dann so aus:
Fall 1)

b
a
b a
 f ( x)dx  lim  f ( x)dx
b
Fall 2)


Fall 3)
Uneigentliche Integrale 1. Art
b
f ( x)dx  lim  f ( x)dx
Uneigentliche Integrale 2. Art
a  a

c

c
b


c
a  a
b c
 f ( x)dx   f ( x)dx   f ( x)dx  lim  f ( x)dx  lim  f ( x)dx
Beispiel zu 1):
Betrachten wir eine Fläche unter dem Graphen von. Die linke Grenze sei
x = 1, nach rechts sei die Fläche unbegrenzt, das Flächenstück erstreckt sich ins
Unendliche (siehe Bild)
Gymnasium „Am Thie“
Blankenburg
Uneigentliche Integrale
Um den Inhalt dieser Fläche zu ermitteln, integrieren wir die Funktion zunächst in den
Grenzen von 1 bis u:
u
1
 1
1 f ( x)dx  x 1   u  1
Lassen wir die obere Grenze u gegen  streben, so strebt der Integralwert offenbar
gegen 1.
1
(  1)  0  1  1
lim
u
u 
Das heißt, der Flächeninhalt unter einer unendlich langen Funktion kann durchaus
endlich sein, in unserem Fall 1 FE.
u
Beispiel zu 2):
Betrachten wir nun die Fläche unter dem Graphen von f ( x) 
1
in den Grenzen
x
von 0 bis 1. An der linken Grenze ist die Funktion nicht definiert, es liegt ein Pol
(Unendlichkeitsstelle) vor.
Um den Inhalt dieser Fläche zu ermitteln, integrieren wir die Funktion zunächst in den
Grenzen von u bis 1:
1

 
f ( x)dx  2 x
1
u
 22 u
u
Lassen wir die linke Grenze u gegen 0 streben, so strebt der Integralwert offenbar
gegen 2.
lim (2  2 u )  2  0  2
u 0
Gymnasium „Am Thie“
Blankenburg
Uneigentliche Integrale
Erweiterung - unendlich lange Rotationskörper
Bsp.: Gesucht ist das Volumen V des unendlich langen Körpers, der durch Rotation
1
der Hyperbel f ( x )  über dem Intervall I [1; ] entsteht.
x
b
Lösung:
2
Va (b)  lim (    f ( x)  dx)
b 
a
b
1
1
 1
dx) = lim (    )  lim(   (  (1)))
2
x
b
b
 x 1
b
1
b
1
 lim (  (1  ))   VE .
b
b
b
 lim (  
Allgemeine Hinweise für Uneigentliche Integrale:
1) Stückweise Integration mit anschließender Addition bei zusammengesetzten
Funktionen (Funktionen, die nebeneinander liegen).
2) Für Funktionen, die untereinander liegen und die Fläche oder der
Rotationskörper zwischen den Funktionen gesucht ist, müssen wir mit der
Differenzfunktion arbeiten.
3) Eigentlich gibt es noch eine vierte grundlegende Form (siehe oben), genau
dann, wenn der Grenzwert nicht gegen Unendlich, sondern gegen Null geht.
Das ist der Fall, wenn z.B. die y-Achse Asymptote der Funktion ist. Die
Lösungsstrategie ist aber analog zu den 3 anderen Formen (siehe auch
Beispiel 2)
Gymnasium „Am Thie“
Blankenburg
Uneigentliche Integrale
Aufgaben:
Berechnen Sie folgende uneigentlichen Integrale, Lösungen in Klammern:


2
1
1)  2 dx
(2 FE)
2)  4 dx
(1/3 FE)
1 x
1 x
3) Die Kurven f und g begrenzen zusammen mit der positiven x-Achse eine Fläche.
Wie groß ist die gesamte Fläche unter den Kurven im I. Quadranten?
1
g ( x)  2
(Lös.: 4/3 FE)
f ( x)  x 2
x
4) Die Kurven f und g begrenzen im I. Quadranten eine Fläche. Wie groß ist die
Fläche zwischen den Kurven im Intervall von 2 bis unendlich?
1
1
f ( x)  2
g ( x)  3
(Lös.: 3/8 FE)
x
x
5) Die Kurven f und g begrenzen zusammen mit der positiven x-Achse eine Fläche.
Wie groß ist das Volumen des Rotationskörpers, der entsteht, wenn diese Fläche um
die x-Achse rotiert.
1
g ( x)  2
f ( x)  x 3
x
Ausführliche Lös.: