DOCX

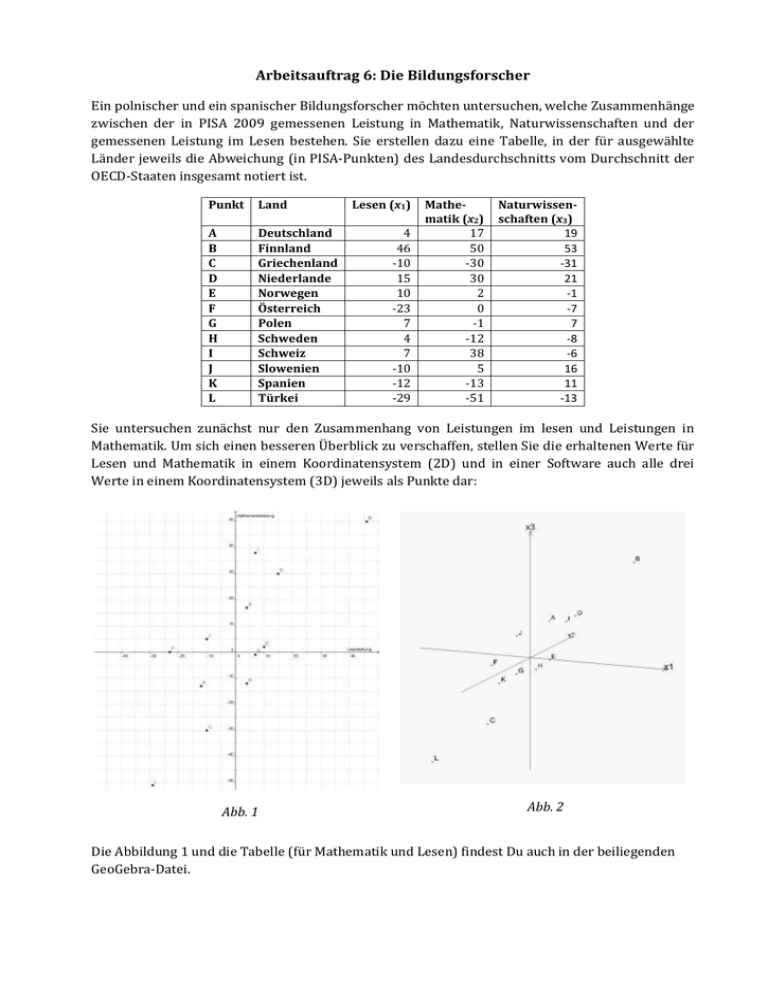
Arbeitsauftrag 6: Die Bildungsforscher
Ein polnischer und ein spanischer Bildungsforscher möchten untersuchen, welche Zusammenhänge
zwischen der in PISA 2009 gemessenen Leistung in Mathematik, Naturwissenschaften und der
gemessenen Leistung im Lesen bestehen. Sie erstellen dazu eine Tabelle, in der für ausgewählte
Länder jeweils die Abweichung (in PISA-Punkten) des Landesdurchschnitts vom Durchschnitt der
OECD-Staaten insgesamt notiert ist.
Punkt
Land
A
B
C
D
E
F
G
H
I
J
K
L
Deutschland
Finnland
Griechenland
Niederlande
Norwegen
Österreich
Polen
Schweden
Schweiz
Slowenien
Spanien
Türkei
Lesen (x1)
4
46
-10
15
10
-23
7
4
7
-10
-12
-29
Mathematik (x2)
17
50
-30
30
2
0
-1
-12
38
5
-13
-51
Naturwissenschaften (x3)
19
53
-31
21
-1
-7
7
-8
-6
16
11
-13
Sie untersuchen zunächst nur den Zusammenhang von Leistungen im lesen und Leistungen in
Mathematik. Um sich einen besseren Überblick zu verschaffen, stellen Sie die erhaltenen Werte für
Lesen und Mathematik in einem Koordinatensystem (2D) und in einer Software auch alle drei
Werte in einem Koordinatensystem (3D) jeweils als Punkte dar:
Abb. 1
Abb. 2
Die Abbildung 1 und die Tabelle (für Mathematik und Lesen) findest Du auch in der beiliegenden
GeoGebra-Datei.
Aufgaben
1)
Der polnische Forscher will die Bildungssysteme in drei speziell ausgewählten Ländern mit
dem von Polen vergleichen. Er sucht dazu jeweils
(L1) ein Land, in dem die Leseleistungen sehr ähnlich wie in Polen sind, die
Mathematikleistungen allerdings deutlich unterschiedlich.
(L2) ein Land, in dem die Mathematikleistungen sehr ähnlich wie in Polen sind, die
Leseleistungen allerdings deutlich unterschiedlich.
(L3) ein Land, in dem sowohl die Leseleistung als auch die Mathematikleistung sehr ähnlich
sind, wie in Polen.
Überlege:
a)
Welche Länder würdest Du ihm jeweils für einen Vergleich empfehlen?
b)
Wie könnte man allgemein (für andere Länder) vorgehen? Wie kann man für ein
beliebiges Land passende „Vergleichsländer“ vom Typ (L1), (L2) und (L3) finden?
c)
Wie könnte man die „Ähnlichkeit“ zwischen zwei Ländern (ggf. mit Methoden der
Vektorrechnung) „ausrechnen“? Was würden diese Rechnungen geometrisch
bedeuten?
2)
Der polnische Forscher erweitert seine Überlegungen auf den Zusammenhang zwischen
Leistungen im Lesen, in Mathematik und Naturwissenschaften. Überlege: Wie findet er ein
Land, dass hinsichtlich aller drei Merkmale möglichst ähnlich zu Polen ist? Wie könnte man
die „Ähnlichkeit“ zwischen zwei Ländern allgemein (ggf. mit Methoden der Vektorrechnung)
„ausrechnen“? Was würden diese Rechnungen geometrisch bedeuten?
3)
Der spanische Forscher behauptet: Für unsere Schüler(innen) ist der Unterschied zwischen
Mathematik- und Leseleistung von allen untersuchten Ländern am Kleinsten.
a)
Durch den Vergleich welcher Werte in der Tabelle ist der spanische Forscher zu dieser
Aussage gekommen?
b)
Wo würden in der Grafik die Länder liegen, für die es überhaupt keinen Unterschied
zwischen Mathematik- und Leseleistung gibt?
c)
Finde verschiedene Möglichkeiten, wie man die Stärke des Unterschieds zwischen
Mathematik- und Leseleistung eines Landes (ggf. mit Methoden der Vektorrechnung)
„ausrechnen“ könnte. Was bedeuten diese Rechnungen geometrisch?
4)
Der spanische Forscher erweitert seine Überlegungen auf den Zusammenhang zwischen
Leistungen im Lesen, in Mathematik und Naturwissenschaften. Überlege: Wie findet er ein
Land, dass sich hinsichtlich aller drei Merkmale möglichst wenig unterscheidet? Wie könnte
man die Stärke des Unterschieds zwischen Mathematik-, Naturwissenschafts- und
Leseleistung eines Landes (ggf. mit Methoden der Vektorrechnung) „ausrechnen“? Was
bedeuten diese Rechnungen geometrisch?
Hinweis: Man kann die Fragen 2) und 4) auf höhere Dimensionen erweitern, in dem man z.B. alle vier
Subskalen des Lesetests getrennt betrachtet, allerdings wirkt die geometrische Vorstellung dann nur
mehr metaphorisch im Sinne des „verallgemeinerten Anschauungsraums“. Die oben verwendeten
Daten, ebenso wie die für eine solche Erweiterung benötigten Daten kann man folgendem Dokument
entnehmen:
http://www.oecd.org/dataoecd/35/35/46615935.pdf