Stochastik auf dem GTR
Werbung

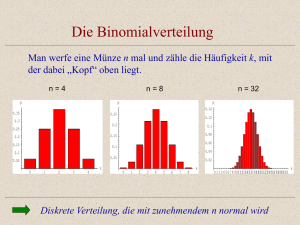
Stochastik mit dem GTR Elemente der Stochastik • Beschreibende Statistik (Kennzahlen von Datenmengen, Regression, Korrelation) • Simulationen – Modellbildung • Wahrscheinlichkeitsberechnungen • Verteilungen und deren Maßzahlen: Binomial- und Normalverteilung, Approximation • Beurteilende Statistik: Testen von Hypothesen, Fehler 1. und 2. Art • MARKOFF-Ketten Mathematik-Menü Menü zur Listenbearbeitung Statistik-Menü Simulation mit Pseudozufallszahlen Vorstellungen von Zufall entwickeln Befehle Bedingungen rand rand(3) rand(10)>0.5 randInt(1,6) randInt(1,6,300) randInt(1,6,300) = 1 Simulation mit Pseudozufallszahlen Einen 100fachen Münzwurf simulieren ... Simulation mit Pseudozufallszahlen ... und die Entwicklung der relativen Häufigkeiten darstellen ... Simulation mit Pseudozufallszahlen Das 300fache Würfeln simulieren ... Simulation mit Pseudozufallszahlen ... und die Entwicklung der relativen Häufigkeiten darstellen ... Simulation mit Pseudozufallszahlen die Bestimmung der absoluten Häufigkeiten automatisieren ... Simulation mit Pseudozufallszahlen Simulation zum 1/e - Gesetz 20faches Werfen eines Ikosaeders 2, 4, 6, 10, 12, 13, 14, 17 fehlen, also 8 von 20 (40%) P(bestimmte Augenzahl tritt nicht auf) 1/e 37% Simulation mit Pseudozufallszahlen Simulation zum 1/e - Gesetz Zufallsregen auf 5x5 -Quadratgitter P(ein Feld bleibt leer) 1/e 37% Simulation mit Pseudozufallszahlen Ziehen mit und ohne Zurücklegen Mit welcher Wahrscheinlichkeit sind die erzeugten Lottozahlen brauchbar? Geburtstagsproblem (Lottoziehung mit Zurücklegen) Wahrscheinlichkeit für lauter verschiedene Glückszahlen Geburtstagsproblem Wahrscheinlichkeit für lauter verschiedene Geburtstage Modellierung von Zufallsversuchen vom Typ „Geburtstagsproblem“ Faustregel: Hat der Zufallsversuch n mögliche Ergebnisse, dann benötigt man ca. 1,2*n Versuchsdurchführungen, damit die Wahrscheinlichkeit für mind. zwei gleiche Ergebnisse über 50% ist. Menü der Wahrscheinlichkeitsverteilungen Hypergeometrische Verteilung Wahrscheinlichkeit für einen Lottogewinn Binomialverteilung Am ersten Schultag werden 206 neue Schülerinnen und Schüler eingeschult. Wie groß ist Wahrscheinlichkeit, dass hierunter (k)ein Geburtstagskind ist (oder vielleicht sogar mehr als eins)? Binomialverteilung - Histogramme Binomialverteilung Bedienungsfehler Binomialverteilung Große Stichprobenumfänge Binomialverteilung - Simulation Simulation einer Binomialverteilung Binomialverteilung - Erwartungswert Erwartungswert einer Binomialverteilung Kumulierte Binomialverteilung Kumulierte Binomialverteilung Kumulierte Binomialverteilung Viele Menschen leiden unter Bluthochdruck. Die Heilungswahrscheinlichkeit eines bestimmten Medikaments beträgt p = 0,8. Mit welcher Wahrscheinlichkeit werden von 72 Patienten - weniger als 50 geheilt? - mehr als 60 geheilt? Binomialverteilung – Streuung um den Erwartungswert Graphen der Größe des Displays anpassen Binomialverteilung – Streuung um den Erwartungswert Graphen der Größe des Displays anpassen Binomialverteilung – Streuung um den Erwartungswert Graphen der Größe des Displays anpassen n Breite Höhe 50 20 0,113 100 30 0,080 200 42 0,057 300 52 0,047 400 62 0,040 Wir beobachten: Mit wachsendem Stichprobenumfang n nimmt die Breite der „Glocken“ mit dem Faktor n zu und die Höhe mit dem Faktor 1/n ab. Binomialverteilung Man kann zeigen: Bei festem n ist die Breite der „Glocken“ proportional zu p(1-p). Bei BERNOULLI-Versuchen konzentrieren sich die Ergebnisse auf eine Umgebung um den Erwartungswert = n p mit einem Radius von ungefähr 3 np(1-p). np(1-p) ist gleich der Varianz der Zufallsgröße. Binomialverteilung - Varianz Varianz – Nachweis der Formel np(1-p) n = 50 ; p = 0,4 n = 100 ; p = 0,2 n = 200 ; p = 0,3 Binomialverteilung - Normalverteilung n = 200 ; p = 0,3 Binomialverteilung – sigma-Regeln P(1-Umgebung) 0.68 P(2-Umgebung) 0.955 Binomialverteilung – sigma-Regeln Bestimmung der Wahrscheinlichkeiten von Umgebungen von Binomialverteilung – sigma-Regeln P(1-Umgebung) 0.68 P(2-Umgebung) 0.955 Binomialverteilung – Approximation durch GAUSSsche Dichtefunktion Binomialverteilung – Approximation durch GAUSSsche Dichtefunktion Binomialverteilung – Approximation durch GAUSSsche Dichtefunktion Binomialtest Entscheidungsregel Bei dominanter Vererbung haben in der zweiten Tochtergeneration 75% der Nachkommen die erste Ausprägung und 25% die andere. Ist bei einem vorliegenden Kreuzungsversuch mit n = 120 die MENDELsche Regel anwendbar? 95%-Umgebung um den Erwartungswert: = 120 0,75 = 90 ; = (1200,750,25) = 4,74 Entscheidungsregel: Verwirf die Hypothese p = 0,75 , falls X < 81 oder falls X > 99 Binomialtest Entscheidungsregel Bei dominanter Vererbung haben in der zweiten Tochtergeneration 75% der Nachkommen die erste Ausprägung und 25% die andere. Ist bei einem vorliegenden Kreuzungsversuch mit n = 120 die MENDELsche Regel anwendbar? Binomialtest Entscheidungsregel 95%-Umgebung um den Erwartungswert: = 120 0,75 = 90 ; = (1200,750,25) = 4,74 Entscheidungsregel: Verwirf die Hypothese p = 0,75 , falls X < 81 oder falls X > 99 Binomialtest Fehler 2. Art Angenommen, die zugrunde liegende Wahrscheinlichkeit ist tatsächlich p = 0,7. Mit welcher Wahrscheinlichkeit wird nicht erkannt, dass hier nicht die MENDELsche Regel zugrunde liegt? P(Fehler 2. Art) = 0,759 Binomialtest Operationscharakteristik Normalverteilung Bestimmung von Mittelwert und Stichprobenstreuung In einer Stichprobe unter 1000 Frauen im Alter zwischen 18 und 20 Jahren fand man die o. a. Verteilung für die Körpergröße. Normalverteilung Approximation durch Normalverteilung Lässt sich die empirische Verteilung durch eine Normalverteilung beschreiben? Normalverteilung Berechnung von Wahrscheinlichkeiten Mit welcher Wahrscheinlichkeit ist die Körpergröße mindestens 1,60 m und höchstens 1,70 m? gesuchte Wahrscheinlichkeit: 56, 3 % Normalverteilung Überprüfung auf Normalverteilung Von 100 neugeborenen Mädchen wurde das Körpergewicht bestimmt. Weisen die Daten darauf hin, dass das Körpergewicht von Neugeborenen normalverteilt ist? Normalverteilung Überprüfung auf Normalverteilung ohne / mit Diagnose Die ultimative Wahlprognose Ausgehend von den Wählerwanderungen zwischen vorletzter und letzter Bundestagswahl gaben wir eine Prognose für den 18. September 2005 ab . . . SPD / Grüne ? CDU/CSU/FDP ? Sonstige Parteien ? Wählerwanderungen 1998 2002 1998 2002 SPD / Grüne CDU/CSU / FDP andere Nichtw. / Erstw. gesamt SPD / Grüne 72,7% 7,0% 19,0% 19,3% 34,7% CDU/CSU / FDP 12,0% 76,5% 13,8% 17,9% 33,8% andere 2,3% 1,3% 37,4% 3,2% 5,2% Nichtw. / gest. 12,9% 15,2% 29,8% 59,6% 26,3% gesamt 100% 100% 100% 100% 100% Übergangsmatrix 33,66% / 73,16% = 46,0% 35,45% / 73,16% = 48,5% Übergangsmatrix Startvektor Produkt Die ultimative Wahlprognose Ausgehend von den Wählerwanderungen zwischen vorletzter und letzter Bundestagswahl ergab sich folgende Prognose: SPD / Grüne 46,0% CDU/CSU/FDP 48,5% Sonstige Parteien 5,5% Matrixpotenzen Niederlassung eines Autovermieters: A, B, C 80% der Fahrzeuge, die am Morgen in A stehen, stehen am Abend wieder in, je 10% sind von A nach B bzw. C gewechselt. Nach B kehren 60% der ausgeliehenen Fahrzeuge wieder zurück; je 20% wechseln nach A oder nach C. Von Niederlassung C aus wechseln erfahrungsgemäß 20% nach A und 10% nach B. Wie viele Fahrzeuge befinden sich an den drei Niederlassungen nach 1, 2, ..., 10, ...20 Tagen, wenn am Anfang je ein Drittel an jeder der drei Niederlassungen vorhanden war? Gibt es eine optimale Aufteilung der Fahrzeug-Bestände? Matrixpotenzen Literaturhinweis „Elemente der Mathematik – Gesamtband Mathematik mit neuen Technologien“ Schroedel 83990 Das Stochastik-Kapitel wurde von mir verfasst und enthält die im Vortrag beschriebenen Einsatzmöglichkeiten des GTR. Heinz Klaus Strick Rückmeldungen erwünscht: [email protected]