Selbstorganisation I
Werbung

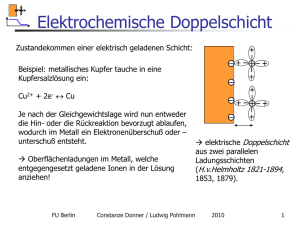
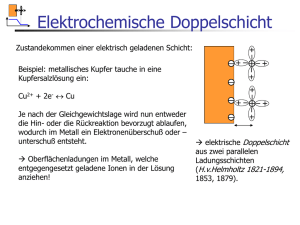
Selbstorganisation Nichtlineare Prozesse in der Elektrochemie 1. Geschichte seltsamer Phänomene Zur Erinnerung: Die Elektrochemie startet als Wissenschaft in Italien: Luigi Galvani (09.09.1737 in Bologna - 04.12.1798 ebenda): „animalische Elektrizität“ Alessandro Volta (18.02.1745 in Como - 05.03.1827 in Camnago bei Como): Elektrometer, Begriff der „Spannung“, Voltasche Säule 1800 FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 1 Selbstorganisation 1. Geschichte seltsamer Phänomene Nur wenig später: Gustav Theodor Fechner (1801 Muskau - 1887 Leipzig): Begründer der Psychophysik (Weber-Fechner-Gesetz), „Atomenlehre“ (1855), Experimente zum Galvanismus: 1828 Tests von Metallpaaren zur Eignung als Stromquellen: Fe / Ag in salpetersaurer Silbernitratlösung: beobachtete eine mehrfach erfolgende Polarisationsumkehr: erste oszillierende elektrochemische Reaktion! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 2 Selbstorganisation 1. Geschichte seltsamer Phänomene John Herschel (1793 Slaugh - 1871 Hawkhurst): Chemiker, Astronom (Sohn von F.W.Herschel): 1833 Passivierungswellen auf einem Eisendraht in Salpetersäure Christian Friedrich Schönbein (1799 Metzingen - 1868 Baden-Baden): Chemiker, erste Brennstoffzelle (1838), Schießbaumwolle, Ozon, oszillierende Passivierung des Eisens James Prescott Joule (1818 Salford - 1889 Sale/Manchester): 1844 Fortsetzung der Schönbeinschen Experimente, Kopplung mit DaniellElementen FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 3 Selbstorganisation 1. Geschichte seltsamer Phänomene Wilhelm Ostwald (1853 Riga - 1932 Leipzig): Oszillierende Auflösung des Chroms in Säuren, Nervenmodell mit Lillie Karl Friedrich Bonhoeffer (1899 Breslau - 1957 Göttingen): Schüler von W. Nernst, Nachfolger von W. Ostwald in Leipzig: ab 1940 Arbeit am OstwaldLillie-Nervenmodell --> gekoppelte Differentialgleichungsmodelle zur Beschreibung der periodischen elektrochemischen Phänomene (Analogie: selbsterregte elektrische Schwingungen) U.F. Franck : Schüler von K.F.B in Göttingen, ab 1950: „Passivierungs-Aktivierungs-Mechanismus“ der Auflösung von Metallen in Säuren „periodische Elektrodenprozesse sind die am längsten bekannten chemischen Oszillationen“ aus: U. F. Franck, Angew. Chem. 90, 1-16 (1978) FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 4 Selbstorganisation 2. Die „ordentliche“ Wissenschaft: Obwohl solche periodische elektrochemische Vorgänge schon lange bekannt waren, galten sie doch als Kuriositäten. Ihnen wurde keinerlei Bedeutung zugemessen, da sie den herrschenden wissenschaftlichen Theorien und Auffassungen widersprachen! Thermodynamik: 2. Hauptsatz: „spontan kann Ordnung nur abnehmen“ (Oszillationen sind aber eine zeitliche Ordnung) Chemische Kinetik: „Edukte und Produkte können nur streng monoton (exponentiell) ab- oder zunehmen; Intermediate durchlaufen höchstens ein Maximum“ --> Ablehnung eingereichter wissenschaftlicher Arbeiten, z.B. Belousov 1950: erste homogen oszillierende Reaktion (Malonsäure/Cer/Bromat) --> Anerkennung erst nach 1961 in der Sowjetunion durch die Arbeiten von Anatoli Zhabotinsky, im Ausland erst ab ca. 1968! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 5 Selbstorganisation 3. Das neue Paradigma: Selbstorganisation in offenen Systemen 2. Hauptsatz der Thermodynamik (Boltzmanns H-Theorem): In einem isolierten System kann die Entropie nur zunehmen (und die Ordnung, Strukturiertheit und Organisation der Systemelemente nur abnehmen). Ilya Prigogines (1917 - 2003) neues Denken: Alles beruht auf einem Denkfehler: die meisten realen Systeme sind nicht isoliert, sie sind thermodynamisch offen: Austausch von Energie und Stoff mit der Umgebung! Darüber aber sagt der 2. Hauptsatz nichts aus! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 6 Selbstorganisation 3. Das neue Paradigma: Selbstorganisation in offenen Systemen Energie und Stoff offenes System Energie und Stoff es ist kein Gleichgewicht mehr möglich, wohl aber ein stationärer Zustand: dEinput = dEoutput und dMinput = dMoutput Im stationären Zustand sind die Bilanzen ausgeglichen. Beispiele: Durchflussreaktor, Brennstoffzelle, katalytisch aktive Grenzfläche! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 7 Selbstorganisation 3. Das neue Paradigma: Selbstorganisation in offenen Systemen Was aber kann man über die Entropie aussagen? Entropiebilanz: dSSystem = dSinput + dSintern - dSoutput = dSext + dSint (Prigogine 1947, 1977 Nobelpreis Chemie) mit dSint > 0 (2. Haupsatz): lokale «Entropieproduktion» aber dSext - beliebig! Hier gibt es keine thermodynamischen Beschränkungen! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 8 Selbstorganisation 3. Das neue Paradigma: Selbstorganisation in offenen Systemen Folgende drei Fälle sind möglich: 1. dSext < 0 , | dSext | > dSint (kein stationärer Zustand): Ordnung im System wird aufgebaut (dS < 0) 2. dSext < 0 , | dSext | = dSint (stationärer Zustand ist erreicht): Ordnung im System wird aufrechterhalten (dS = 0) 3. dSext > - dSint (kein stationärer Zustand): Ordnung im System wird abgebaut (dS > 0) Fern vom Gleichgewicht können Ordnung und Struktur spontan entstehen! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 9 Selbstorganisation 4. Dissipative Strukturen - eine neue Sicht altbekannter Vorgänge Prigogines Umbruch im wissenschaftlichen Denken rückte die bisherigen „Randerscheinungen“ und „Kuriositäten“ plötzlich ins Zentrum der Wissenschaft! Gleichzeitig verschob sich der Schwerpunkt von einer statischen und linearen Betrachtungsweise zur Erforschung nichtlinearer Prozesse, in denen die Zeit eine wesentliche Rolle spielt. Dynamische Ordnung, Nichtlinearität, Komplexität und Netzwerke werden zu den neuen Schlagwörtern. FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 10 Selbstorganisation 4. Dissipative Strukturen - eine neue Sicht altbekannter Vorgänge dissipativen Strukturen in der Natur: Bénard-Effekt: Wolkenstraßen, Magmakonvektion, Sonnengranulation, Basaltsäulen chemische Oszillationen: Belousov-Zhabotinsky-Reaktion, Briggs-RauscherReaktion, Biologische Uhren elektrochemische Oszillationen gesellige Amöben: Dictyostelium discoideum dissipativ-fraktale Strukturen: Schneeflocken, Dendriten (Diffusionslimitierte Aggregation (DLA), MullinsSekerka-Instabilität) Liesegang-Ringe FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 11 Selbstorganisation 4. Dissipative Strukturen - eine neue Sicht altbekannter Vorgänge thermodynamischer Ast, Lineare Näherung zweite Bifurkation erste Bifurkation Entfernung vom Gleichgewicht FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 12 Selbstorganisation 4. Dissipative Strukturen - eine neue Sicht altbekannter Vorgänge Aus der Linearität folgt: es gibt nur einen stationären Zustand dieser Zustand ist stabil (Minimum der Entropieproduktion) dieser Zustand geht stetig in den Gleichgewichtszustand über Im linearen Bereich können keine qualitativ neuen Strukturen entstehen (kein Symmetriebruch möglich)! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 13 Selbstorganisation 5. Stabilität und Instabilität Neue (dissipative) Strukturen entstehen, wenn der bisherige stationäre Zustand, der den thermodynamischen Zweig repräsentiert, instabil wird - und (mindestens) ein neuer stabiler Zustand auftritt, welcher die neue zeitliche, räumliche oder raumzeitliche Struktur darstellt. Der Stabilitätsbegriff nimmt also eine Schlüsselstellung ein! Mechanische Analoga: 1. Asymptotische Stabilität Regelung: strukturstabil, robust negative Rückkopplung FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 14 Selbstorganisation 5. Stabilität und Instabilität 2. Einfache Stabilität = Neutrale Stabilität (= neutrale Instabilität): --> es gibt ein Kontinuum von möglichen Zuständen --> eine Störung führt zu einem benachbarten Zustand --> nicht robust, nicht strukturstabil Beispiel: harmonischer Oszillator: eine solche Uhr würde niemals genau gehen können! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 15 Selbstorganisation 5. Stabilität und Instabilität 3. (Exponentielle) Instabilität jede noch so kleine Störung führt dazu, daß die Triebkraft, welche vom Zustande wegtreibt, stärker wird: selbstbeschleunigtes Entfernen vom Zustand positive Rückkopplung Beispiele: Mikrofon-Lautsprecher-Rückkopplung, Lawine, Explosion, Autokatalyse FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 16 Selbstorganisation 6. Skizze der mathematischen Stabilitätsanalyse Welche mathematische Entsprechung hat die intuitive mechanische Analogie der Stabilität? Newtonsches Bewegungsgesetz: d 2x dx m 2 F x dt dt F Näherungsweise bei starker Reibung : x dx F x a x dt a0 Das lässt sich verallgemeinern: Die Bewegung einer Variablen um einen stationären Punkt ist asymptotisch stabil, wenn die Änderungsgeschwindigkeit proportional zur Abweichung davon ist und das umgekehrte Vorzeichen besitzt! Dabei ist die konkrete Form der Funktion F(x) unwesentlich, wichtig ist nur die lineare Näherung (erste Ableitung, Tangente), um die Stabilität zu bestimmen! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 17 Selbstorganisation 6. Skizze der mathematischen Stabilitätsanalyse Analoges gilt für den Fall der Instabilität: Näherungsweise bei starker Reibung : dx F x a x dt F a0 x Verallgemeinert:: Die Bewegung einer Variablen um einen stationären Punkt ist instabil, wenn die Änderungsgeschwindigkeit proportional zur Abweichung davon ist und das gleiche Vorzeichen besitzt! Wieder ist die konkrete Form der Funktion F(x) unwesentlich, wichtig ist nur die lineare Näherung (erste Ableitung, Tangente) für die Stabilität! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 18 Selbstorganisation 6. Skizze der mathematischen Stabilitätsanalyse Etwas genauer mathematisch definiert, für eine Variable: dX F(X ) dt F(X 0 ) 0 ursprüngliche nichtlineare Gleichung Nullstelle der Funktion = stationärer Zustand Für die Stabiltät ist nur die (kleine) Abweichung vom stationären Zustand wichtig: dF X X 0 x F ( X 0 x) F ( X 0 ) dX dx dF x da dX dx dt dX X 0 dt dt FU Berlin Constanze Donner / Ludwig Pohlmann X0 dF x dX x X0 Reihenentwicklung 2011/2012 19 Selbstorganisation 6. Skizze der mathematischen Stabilitätsanalyse Stabilitätsgleichung für eine Variable: dX F(X ) dt dx dF dt dX x ax X0 Allein das Vorzeichen der ersten Ableitung der Funktion im Stationären Zustand ist entscheidend für die Stabilität des Zustandes selbst: a >0: instabil, exponentielles Wachstum der Abweichung (Repellor) a = 0: einfach stabil, Abweichungen bleiben konstant a >0: asymptotisch stabil, Abweichung wird immer kleiner (Attraktor) FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 20 Selbstorganisation 6. Skizze der mathematischen Stabilitätsanalyse Beispiel: Schlögl-Reaktion mit einer Autokatalyse 3. Ordnung: A 2 X 3 X , B X C , A, B, C const Kinetische Gleichung für den Autokatalysator: dX k1 AX 2 k1' X 3 k 2 BX dt Mit den stationären Zuständen (Konzentrationen): dX F(X ) dt FU Berlin dx dF dt dX X 1 0, X 3 X 2 0 x ax X0 Constanze Donner / Ludwig Pohlmann 2011/2012 21 Selbstorganisation 6. Skizze der mathematischen Stabilitätsanalyse Erste Ableitung: a( X ) dF 2k1 AX 3k1' X 2 k 2 B dX F(X) a( X 1 ) k 2 B 0 X X1=0 X2 X3 a<0 a>0 a<0 stabil instabil stabil FU Berlin Constanze Donner / Ludwig Pohlmann Autokatalyse findet nur bei Überschreiten des Schwellwertes X2 statt! 2011/2012 22 Selbstorganisation 6. Skizze der mathematischen Stabilitätsanalyse Verallgemeinerung auf mehrere Variablen (z.B. die Konzentrationen mehrerer Intermediate: Differentialgleichungssystem Linearisierung Eigenwertproblem: N Variable N Eigenwerte (meist komplex) Entscheidend für die Stabilität aber ist nur der Realteil: 1) mindestens ein Realteil ist > 0: Instabilität, Repellor 2) alle Realteil sind < 0: asymptotische Stabilität, Attraktor FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 23 Selbstorganisation 6. Skizze der mathematischen Stabilitätsanalyse Begriff des Phasenraumes zur Veranschaulichung der Bewegung nichtlinearer Systeme: Raum aller abhängigen Variablen (z.B. Konzentrationen), die unabhängige Variabel Zeit ist nur noch indirekt enthalten. Jeder Systemzustand ist dann nur ein Punkt im Phasenraum, und jede Zustandsänderung ist eine Trajektorie (Bahnkurve) darin. 1) Trajektorien können sich nicht schneiden 2) nur im stationären Zustand (Punkt) sammeln sich unendlich viele Trajektoren Folgerungen: 1. bei nur einer Variablen (eindimensionaler Phasenraum) kann es zwar Multistabilität geben (z.B. 2 stabile Zustände im Schlögl-Modell), aber Oszillationen sind nicht möglich! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 24 Selbstorganisation 6. Skizze der mathematischen Stabilitätsanalyse Weitere Folgerungen: 2. erst ab zwei Variablen (zweidimensionaler Phasenraum) sind Oszillationen möglich ( = geschlossene Kurven im Phasenraum)! 3. Mehrfachoszillationen und dynamisches Chaos sind erst ab drei Variablen (dreidimensionaler Phasenraum) möglich! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 25 Selbstorganisation 7. Nichtlineare elektrochemische Systeme: Bistabilität Bistabilität am Beispiel der Passivierung des Eisens(1 molare H2SO4): i negativer differentieller Widerstand! O2 E (V) vs. NHE -0.25V 0.58V 2.0V Flade-Potential FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 26 Selbstorganisation 7. Nichtlineare elektrochemische Systeme: Bistabilität Ersatzschaltbild einer elektrochemischen Reaktion: DL – Potentialabfall in der Doppelschicht R – Potentialabfall am Außenwiderstand (load) FU Berlin Constanze Donner / Ludwig Pohlmann Uext = DL + R (potentiostatisch) 2011/2012 27 Selbstorganisation 7. Nichtlineare elektrochemische Systeme: Bistabilität Gleichung für die Strombilanz unter Berücksichtigung der Doppelschichtladung: d DL I I Faraday DL C DL R dt d DL U DL C DL I Faraday DL dt R dDL U DL C DL nF [ A]k (DL ) dt R Strombilanz da: Uext = DL + R nach Einsetzen der Faraday-Reaktion (Butler-Volmer) k(): nichtlineare Differentialgleichung für den Spannungsabfall in der Doppelschicht FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 28 Selbstorganisation 7. Nichtlineare elektrochemische Systeme: Bistabilität Stabilitätsuntersuchung: Ableitung der rechten Seite nach DL : a nF [ A] dk (DL ) 1 dDL R Wann ist ein Zustand instabil: wenn a > 0, d.h. wenn: dk ( DL ) 0 d DL und dk ( DL ) 1 nF [ A] d DL R im Bereich des stationären Zustandes muss die i-U-Kennlinie einen negativen Anstieg haben (negativer differentieller Widerstand), und dieser muss dem Betrage nach den Ohmschen Vorwiderstand überschreiten! FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 29 Selbstorganisation 7. Nichtlineare elektrochemische Systeme: Bistabilität Bistabilität am Beispiel der Passivierung des Eisens (1 molare H2SO4): i Widerstandsgerade (load line) Anstieg: instabil! O2 - 1/R stabil 1 stabil 2 E (V) vs. NHE -0.25V 0.58V 2.0V Flade-Potential FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 30 Selbstorganisation 7. Nichtlineare elektrochemische Systeme: Bistabilität Bistabilität am Beispiel der Passivierung des Eisens (1 molare H2SO4): Fazit für das Passivsystem: 3 Schnittpunkte = 3 stationäre Zustände, davon 2 stabil: Hochstromzustand (aktiv): Fe-Auflösung links vom Flade-Potential und Niedrigstromzustand (passiv): nur Sauerstoffentwicklung rechts vom FladePotential Bistabilität Andere Ursachen negativer differentieller Widerstände: Auskristallisieren des gebildeten Metallsalzes, Adsorptionseffekte, Frumkineffekt FU Berlin Constanze Donner / Ludwig Pohlmann 2011/2012 31